四轮驱动车辆路面附着系数实时估计

赵立军，邓宁宁，葛柱洪，刘昕晖

（1.哈尔滨工业大学（威海）汽车工程学院，264209山东威海；2.吉林大学机械科学与工程学院，130025长春）

四轮驱动车辆路面附着系数实时估计

赵立军1，2，邓宁宁1，葛柱洪1，刘昕晖2

（1.哈尔滨工业大学（威海）汽车工程学院，264209山东威海；2.吉林大学机械科学与工程学院，130025长春）

针对目前无法直接测得车辆路面附着系数的问题，通过设计扩张状态观测器及利用递推最小二乘法来实时估计该值.建立7自由度车辆模型，给出车轮受力平衡方程，设计二阶非线性扩张状态观测器.根据轮胎驱动转矩及车轮转速估计当前利用附着系数，并对观测器进行仿真.结果表明，观测器能够有效观测利用附着系数.在已观测出的利用附着系数的基础上，推导了利用附着系数与峰值附着系数间的递推公式，利用递推最小二乘法设计峰值附着系数估计器，并在Matlab／Simulink中进行仿真.结果表明，估计器可以较为快速有效地实现峰值附着系数识别，较为准确地实时估计附着系数.

四轮驱动车辆；利用附着系数；扩张状态观测器；峰值附着系数

对于各轮驱动转矩可以分别单独控制的四轮驱动车辆而言，其优点之一就是可以根据路面的附着条件，尽量给路面附着条件较好的驱动轮多分配驱动转矩，而给附着条件较差的驱动轮减小驱动转矩以免车轮打滑使车辆处于不稳定工况.因此，路面峰值附着系数及利用附着系数等路面信息的实时估计显得尤为重要.但目前在车辆上很难快速地直接测得利用附着系数的值.文献［1］研究了通过多种传感器收集车辆行驶参数来预测路面附着系数；文献［2］设计了实时牵引力估计器来估计最大路面摩擦系数，又利用μ-S（附着系数-滑转率）曲线的斜率研究路面附着系数信息；文献［3-4］利用车辆的回正力矩估算路面附着系数；文献［5］用模糊控制的方法将车辆在小附着系数区域的路面利用附着系数估高，实现对路面的识别；文献［6］则利用模糊控制理论，以电动汽车为基础进行了利用附着系数的识别.但是上述方法在实时性方面都存在一定不足.

本文设计了状态观测器来对路面附着系数状况进行估计.车辆行驶过程中车轮转速ω可以直接通过转速传感器测得，然后利用驱动转矩及转速信息即可实时估算出当前车轮的利用附着系数.

路面峰值附着系数的估计有多种方法：文献［7］提出了一种采用抛物线函数拟合μ-S曲线的方法来得到关于峰值附着系数的信息；文献［8］则通过计算车轮动力学参数的导数变化得到关于峰值附着系数的信息；文献［9］设计了一种高通滤波器来观测路面附着系数；文献［10］则根据μ-S曲线斜率的变化识别路面峰值附着系数.由于存在实时性的问题，本文提出了另外的一种方法.即在已观测到的利用附着系数的基础之上，利用简化的轮胎模型中峰值附着系数与利用附着系数之间的关系推导了基于递推最小二乘算法的递推公式，以此公式为依据，设计了峰值附着系数估计器来估计路面峰值附着系数.

1 四轮驱动车辆动力学建模

为了对路面附着系数估计算法进行研究，建立了包括整车纵向、侧向、横摆以及4个车轮转动的7自由度四轮驱动车辆非线性模型．选取整车质心为坐标系原点，纵向对称轴为χ轴，并以车辆行驶方向为正方向，侧向为y轴，垂直于地面方向为z轴，向上为正．其沿χ轴、绕z轴、沿y轴的动力学方程分别如下：

式中：m为整车质量（kg），Fχ为轮胎纵向力（N），Fy为轮胎侧向力（N），Fw为整车空气阻力（N），Ff为整车滚动阻力（N），Iz为整车质量绕z轴的转动惯（kg·m2），S为轮距（m），δf为前轮转角（rad），u为车辆质心处侧向速度（m／s），v车辆质心处纵向速度（m／s），ωr为车辆横摆角速度（rad／s），lf、lr分别为车辆前轮和后轮到质心处的距离（m），fl，fr，rl，rr分别代表前左轮，前右轮，后左轮，后右轮.

假设4个车轮规格相同，如图1所示为驱动轮受力平衡图.在车轮坐标系W下驱动轮转动力矩平衡方程为

式中：Jw为车轮转动惯量（kg·m2），Td为车轮驱动力矩（N·m），f为车轮滚动阻力系数，R为车轮的滚动半径（m），ij代表fl，fr，rl，rr.

图1 驱动轮受力平衡图

轮胎纵向滑移率Sχ的计算公式为

式中：ω为轮胎旋转的角速度（rad／s），R为轮胎的有效滚动半径（m），Vχ为轮胎中心的纵向速度（m／s）.

轮胎中心的纵向速度计算方法为

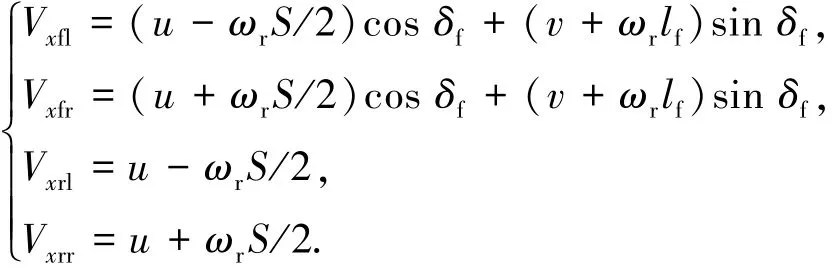
各车轮垂直载荷计算公式为

式中：L为前后轴轴距（m），hg为质心高度（m），aχ为车辆纵向加速度（m／s2），ay为车辆侧向加速度（m／s2）.

国内外对轮胎的特性从各个角度进行了详细的研究.其中，魔术公式因为模拟准确性较高而影响力较大.因此本文采用Pacejka非线性轮胎模型（魔术公式）来较为精确地描述轮胎力学特性［11］.

2 基于扩张状态观测器的利用附着系数估计

本文构造扩张状态观测器来观测驱动轮的利用附着系数，具体设计过程如下.

驱动轮转动的力矩平衡方程见式（1）.利用附着系数的定义可以得到以下关系式：

整理式（1）和（2）可得

可以观察到式（3）为关于车轮转动角速度ω的一阶非线性系统．驱动力矩Tdij为系统输入，含有利用附着系数μχij的项视作系统的外部未知扰动，并将其作为系统新的扩张状态变量χ2［12］．综上所述，得到下面的定义：

通过式（4）将原来的一阶非线性系统重构为新的二阶非线性系统，其状态空间表达式为

为了观测状态变量χ1和χ2，设计二阶非线性扩张状态观测器，表达式为

式中：u和y是观测器的输入信号；z1和z2为χ1和χ2的观测值；b0为增益系数b的估计值；β01、β02为观测器系数．图2为扩张状态观测器原理示意图．

图2 扩张状态观测器原理示意图

很显然，由于Jw为已知值，故b＝1／Jw为已知．由式（4）可知：

本文将滚阻系数f取为一定值.

扩张状态观测器系数β01、β02的确定较为困难．中科院韩京清提出了扩张状态观测器系数与斐波那契数列相关的确定方法［13］，根据该方法有

其中h为系统的仿真步长．

根据上述方法只得到观测器系数的大致值，因此还需要在此基础上，在Simulink中不断仿真调试，最终得到β01和β02合适值，经调试后β01和β02的合适值为β01＝800，β02＝30 000．

对于上述模型用两种工况进行仿真验证，参数分别为：α1＝1，α2＝0.1，δ＝0.2，Tdij＝250 N·m，u＝20 m／s；α1＝1，α2＝0.1，δ＝0.2，Tdij＝150 N·m，u＝10 m／s.

仿真结果如图3所示.

图3 利用附着系数估计结果

为了验证该扩张状态观测器的有效性，将该模块应用到7自由度车辆模型中.图3为扩张状态观测器对左前轮利用附着系数的观测结果.从图中可以看到：开始时，两组仿真结果中利用附着系数均存在较大波动误差，但其误差很快地减小，最终与实际利用附着系数较为吻合.因此，该观测器可以准确快速地完成参数估计任务，且具有较好的鲁棒性.

3 路面峰值附着系数的辨识

在目前实际条件下，车辆上没有技术条件来实时对路面情况进行直接测量.因此表征路面附着条件的附着系数只能通过观测器来间接地估计.

3.1 简化轮胎模型

尽管魔术公式对轮胎力学特性描述较好，但其数学形式比较复杂，这导致其多用于计算机仿真.本文建立的控制系统对实时性有较高要求，因此需要控制系统中的轮胎模型形式简单且有足够高的精度.通过查阅相关文献，得到一种相对精确且参数较少的简化轮胎模型公式，其形式如下［14］：

式中：μp为峰值附着系数，Sp为峰值附着系数对应的滑转率值，S为滑转率．

从图4可以看到，简化轮胎模型公式与魔术公式在线性区域拟合较好，能够用于估计峰值附着系数.

图4 简化轮胎模型公式与魔术公式

从式（5）中可以明显地看出轮胎的利用附着系数与峰值附着系数之间的关系，由此关系式可以推导基于递推最小二乘算法的递推公式，在此公式的基础上设计峰值附着系数估计器就可以估计路面峰值附着系数.基于此原理，下设a＝2μpSp，b＝Sp2，则可将式（5）变换为适于估计的线性形式：

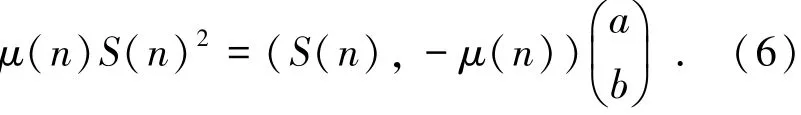
3.2 递推最小二乘路面参数估计器设计及仿真

递推最小二乘法（RLS）的递推公式如下［15］：

式中：P（k）为协方差矩阵，λRLS为遗忘因子，y（k＋1）为测量系统输出，I为适当维数的单位矩阵．

λRLS是新数据的权系数，其始终大于旧数据的权系数，实现逐渐遗忘掉过去数据的作用［16］．该因子取值范围一般是0.950≤λRLS≤0.995，本文中取值为0.970．

将式（6）中的部分参数做出如下定义：

图5为RLS参数估计的原理图.

图5 RLS参数估计原理

为了验证RLS参数估计的有效性，取两组值进行仿真验证.令P（0）初始值为［3 0；0 3］，θ（0）＝［0 0］，其中一组轮胎峰值附着系数为0.8，峰值附着系数对应的滑转率为0.2，其估计的正确结果应该为a＝0.32，b＝0.04；另一组轮胎峰值附着系数为0.7，峰值附着系数对应的滑转率为0.1，其估计的正确结果应该为a′＝0.14，b′＝0.01．为了验证上述结果的正确性，根据式（5）～（10）搭建Simulink模型并进行仿真，得到参数估计结果，如图6所示.

图6 RLS参数估计仿真结果

由图6可以看出，估计值a、b、a′和b′均以较快的速度达到了稳定状态，并且其稳定值均与预期结果相等．因此该参数估计方法可以准确快速地完成参数估计任务．

在车辆行驶过程中，根据驱动转矩和驱动轮转速实时估计当前车轮的利用附着系数，进而利用递推最小二乘估计器对当前路面的峰值附着系数进行估计，从而为车辆的驱动转矩分配提供控制依据.整个路面识别系统的原理框图如图7所示.

为了验证该路面识别系统的有效性，选择两种路面情况进行验证，搭建Simulink仿真模型.在车辆直行工况下，设定其初始条件为：各轮分配的驱动转矩Td＝250 N·m，车速Vχ＝20 m／s，仿真结果如图8所示.

图7 路面识别系统整体构架示意图

图8 路面识别系统仿真结果

4 结 论

1）分析了四轮驱动车辆车轮受力情况，并据此设计了二阶非线性扩张状态观测器，该观测器根据当前车轮转速以及驱动转矩来估计当前利用附着数.仿真结果表明，扩张状态观测器能够有效地估计利用附着系数.

2）根据利用附着系数的估计结果，用简化的轮胎模型推导出了递推公式，根据最小二乘原理设计了峰值附着系数估计器.仿真结果表明，估计器能够快速有效地估计当前路面状态.

［1］LI L，SONG J，LI H Z，et al.Comprehensive prediction method of road friction for vehicle dynamics control［J］. Journal of Automobile Engineering，2009，223（8）：987-1002.

［2］LEE C，HEDRICK K，KYONGSU Y.Real⁃time slip⁃basedestimationofmaximumtire⁃roadfriction coefficient［J］.IEEE／ASMETransactionson Mechatronics，2004，9（2）：141-143.

［3］ONO E，ASANO K，KOIBUCHI K.Estimation of lateral tire grip margin using electric power steering system［C］／／Proceedingsof18thIAVSDSymposium，Dynamics of Vehicles on Road and Tracks.Atsugi：IAVSD，2003：141-143.

［4］SUI Y，TANAKA W，MURAGISHI Y，et al.Estimation of lateral grip margin based on self⁃aligning torque for vehicle dynamics enhancement［J］.SAE Paper，2004，2004-01-1070.

［5］李刚，宗长富，张强，等.基于模糊路面识别的4WID电动车驱动防滑控制［J］.华南理工大学学报：自然科学版，2012，40（12）：99-104.

［6］KATAOKA H.Optimal slip ratio estimator for traction control systemofelectricvehiclebasedonfuzzy inference［J］.The Transactions of the Institute of Electrical Engineers of Japan，2000，35（3）：56-63.

［7］王强.基于横摆力矩和变滑转率联合控制的电子差速控制系统研究［D］.杭州：浙江大学，2004.

［8］靳立强，王庆年，宋传学.电动轮驱动汽车的最佳车轮滑移率实时识别［J］.吉林大学学报：工学版，2010，40（4）：889-894.

［9］余卓平，左建令，陈慧.基于四轮轮边驱动电动车的路面附着系数估算方法［J］.汽车工程，2007，29（2）：141-145.

［10］FUJIMOTO H，FUJII K，TAKAHASHI N.Vehicle stability control of electric vehicle with slip⁃ratio and cornering stiffness estimation［C］／／Proceedings of the 2007IEEE／ASMEInternationalConferenceon Advanced Intelligent Mechatronics.Zurich：ETH Zurich，2007：1-6.

［11］PACEJKA H B，BAKKER E.The magic formula tyre model：Vehiclesystemdynamics，vehiclesystem dynamics［J］.InternationalJournalofVehicle Mechanics and Mobility，1992，21：1-18.

［12］黄一，韩京清.非线性连续二阶扩张状态观测器的分析与设计［J］.科学通报，2000，45（13）：1373-1379.

［13］韩京清.扩张状态观测器参数与斐波那契数列［J］.控制工程，2008，15：1-3.

［14］QIAN Ming.Sliding mode controller design for ABS system［D］.Virginia：Virginia Polytechnic Institute and State University，2004.

［15］SADO H，SAKAI S，HORI Y.Road condition estimation for traction control in electric vehicle［C］／／ISIE’99⁃Bled.Slovenia：［s.n.］，1999：973-978.

［16］AOKI J，MURAKAMI T.A method of road condition estimation and feedback utilizing haptic pedal［C］／／IEEE InternationalWorkshoponAdvancedMotion Control.Piscataway：IEEE press，2008：777-782.

（编辑 杨 波）

Real⁃time road condition estimation for four⁃wheel⁃drive vehicle

ZHAO Lijun1，2，DENG Ningning1，GE Zhuhong1，LIU Xinhui2

（1.School of Automobile Engineering，Harbin Institute of Technology（Weihai），264209 Weihai，Shandong，China；2.College of Mechanical Science and Engineering，Jilin University，130025 Changchun，China）

The road condition can be estimated by the extended state observer and the recursive least square method based on a 7DOF nonlinear vehicle model.in which the wheel force is analyzed，the force equilibrium equation is put forward and then the second order nonlinear extended state observer is designed.The results show that the extended state observer can achieve the observation of the utilization adhesion coefficient.Then a recurrence formula is derived based on the simplified tire model.The model shows the relationship between the utilization adhesion coefficient and the peak adhesion coefficient.The peak adhesion coefficient estimator is designed based on the recursive least square method，and the Matlab／Simulink simulation results show that the estimator can identify the peak adhesion coefficient quickly.The adhesion coefficient estimator can obtain the real⁃time estimation accurately.

four⁃wheel⁃drive vehicle；utilization adhesion coefficient；extended state observer；peak adhesion coefficient

U461

：A

：0367-6234（2014）11-0042-05

2013-12-12.

国家自然科学基金（51275126）；威海市科技发展计划项目（2012DXGJ13）.

赵立军（1975—），男，博士后，副教授.

赵立军，zhaolijun＠hitwh.edu.cn.