基于摄像测量法的在轨柔性结构模态参数辨识
许 畅,王 聪,高晶波,张春芳
(哈尔滨工业大学航天学院,150001哈尔滨)
在轨柔性结构是指卫星主体以外的柔性附件,包括太阳能帆板,天线等.这些柔性附件的自由振动具有低频、密频的特点[1-3].在轨时飞轮或推力器工作会引起柔性附件长时间振动,产生低频扰动力矩,给卫星姿态稳定性带来了较大的影响[4-6].柔性附件的模态参数对卫星姿态控制和振动控制至关重要,但由于其尺寸较大,且在轨空间环境复杂,地面模态测试难以获得所需精度,因此,在轨模态辨识方法受到越来越多的重视[7-9].
传统的位移/加速度传感器由于设备复杂,会大大降低在轨结构的可靠性,也增加了有效载荷的质量和成本.同时,接触性测量也会影响柔性结构的动态性能,数字摄像测量能在实现非接触测量的同时保证较高的精度,而且能降低传感器带来的在轨设备复杂度和成本,是非常有前景的一种在轨响应测量方法.
摄影测量是基于专业摄像设备和数字图像处理算法的测量技术,被广泛应用于物体几何尺寸和空间位置、姿态等测量.Chang等[10]对建筑结构振动进行了摄像测量,采用数字图像相关法进行测点特征匹配;Barrows[11]将摄像测量法用于风洞实验模型形变的测量;Burner等[12]利用摄影测量技术进行了机翼形变测量;Ryall等[13]采用单相机测量法实现了对机翼的振动测量.在航天领域,NASA早在1996年就利用摄像测量技术获得了和平号空间站太阳能帆板的在轨动力学特性[14],1998年NASA还利用摄像测量法获得了不同环境下哈勃望远镜太阳帆版的变形信息[15],这些测量任务都是在航天飞机上完成的.对于大型星载天线,由于其结构较太阳能帆板复杂,对摄像测量系统要求更高.国内利用摄像测量进行结构振动测试的文献较少,一般只针对大型柔性附件进行有限元分析以获得其在轨动态特性,其精度往往难以满足要求.
本文提出一种基于数字摄像测量的柔性星载天线的在轨模态辨识方法,利用两台或以上摄像机测量柔性天线在轨动态响应,如图1所示.其关键技术包括相机标定,像素提取和三维重构及辨识算法等.利用天线模型和两台高速摄像机进行了实验验证,测得了各个测点的振动曲线,并成功地辨识出了天线模型前5阶固有频率和阻尼比,为在轨柔性结构模态参数辨识提供了一种有效的方法.
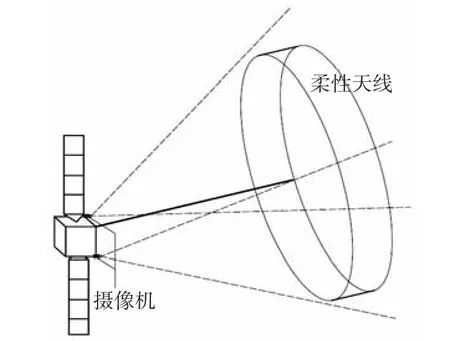
图1 星载柔性天线在轨响应的摄像测量
1 双目三维重构技术
1.1 三维动态重构
图像三维重构是指利用两个或两个以上相机对被测物进行成像,然后从图像中获得物体三维坐标的过程,过程中涉及4个坐标系,分别为:
1)世界坐标系——根据自然环境所选定的坐标系,坐标值用(Xw,Yw,Zw)表示;
2)图像坐标系——坐标原点在CCD图像平面的中心,X轴、Y轴分别为平行于图像平面的两条垂直边,坐标值用(x,y)表示;
3)像素坐标系——坐标原点在CCD图像平面的左上角,X轴、Y轴分别平行于图像坐标系的X轴和Y轴,坐标值用(u,v)来表示;
4)光心坐标系——以相机的光心为坐标原点,X轴、Y轴分别平行于图像坐标系的X轴和Y轴,相机的光轴为Z轴,坐标值用(Xc,Yc,Zc)表示.三维重构的步骤是将像素坐标系转换到图像坐标系,再从图像坐标系转换到光心坐标系,最后由光心坐标系转换到世界坐标系.最终像素坐标和世界坐标可由如下关系表述:
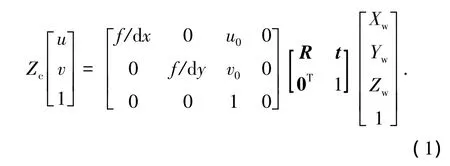
式中:(u0,v0)是图像坐标系原点在像素坐标系中的坐标;(dx,dy)分别是像素坐标系在x方向和y方向相邻像素间的距离;f为相机焦距;R和t是旋转矩阵和平移矩阵.可将式(1)简化成
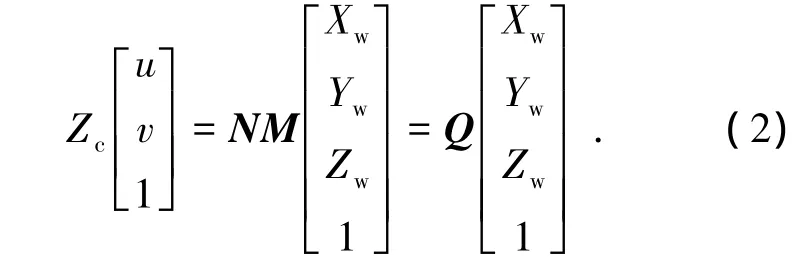
式中:N为相机的内部参数矩阵,包含了相机的焦距,像素单元距离等自身参数;M为相机的外部参数矩阵,包括了相机安装位置和角度等信息;Q为投影矩阵.通过两个相机同时拍摄被测点,可以建立以下方程组:
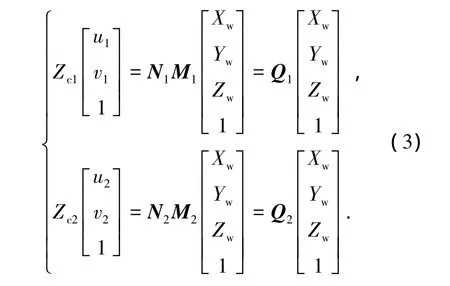
当相机内外参数Q1,Q2已知,则上式消去Zc1和Zc2后得到3个未知数4个方程,可解得被测点的世界坐标值,理论上采用的摄像机数目越多,得到的结果越精确.利用不同时刻拍摄得到的图像序列,就可以得到测点的位移振动曲线,完成对测点的三维动态重构.
1.2 相机标定
将式(2)改写成
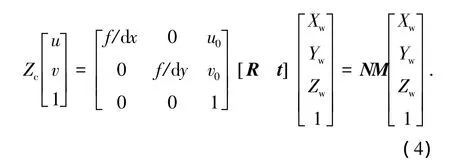
相机的内部参数包括f、(dx,dy)及(u0,v0),内参数标定方法有很多,本文采用张正友标定法[16].当内部参数已经确定时,可以进行外部参数的标定,以下重点叙述用于三维重构的相机外参数标定方法.
从式(4)可见内部参数矩阵N为满秩矩阵,令:αx=dx/f;αy=dy/f,用N-1左乘式(4)的两边并整理得
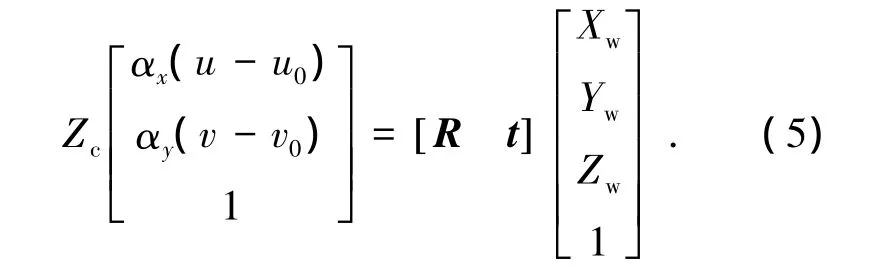
令k=αx(u-u0),l=αy(v-v0),M=Rt[ ],进一步将式(5)改写成
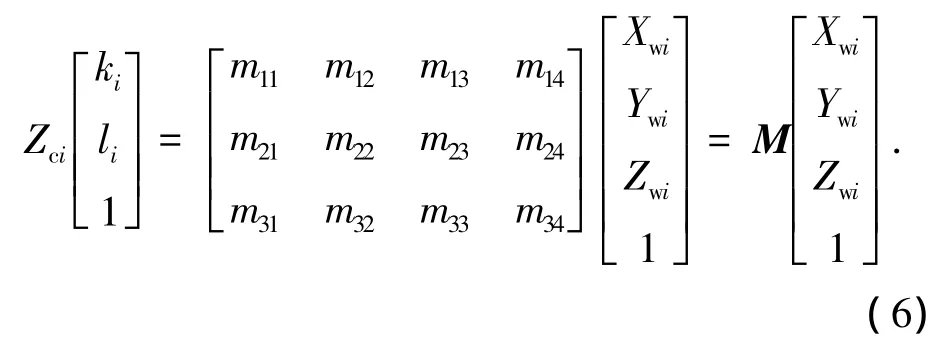
其中:(Xwi,Ywi,Zwi)是世界坐标系中的第i点坐标,(ki,li)是由对应的图像像素坐标(ui,vi)的计算值.
将式(6)展开可得到如下3个方程:
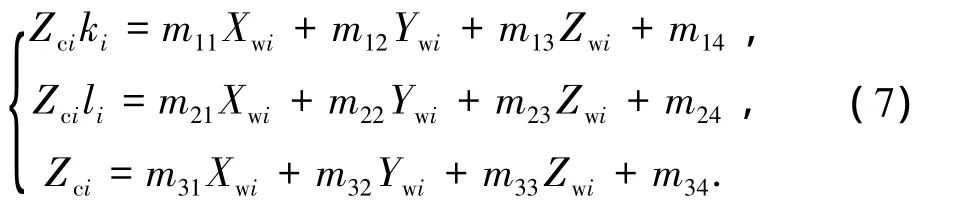
将式(7)中的第3式分别代入上两式消去Zci可得到如下两个方程:
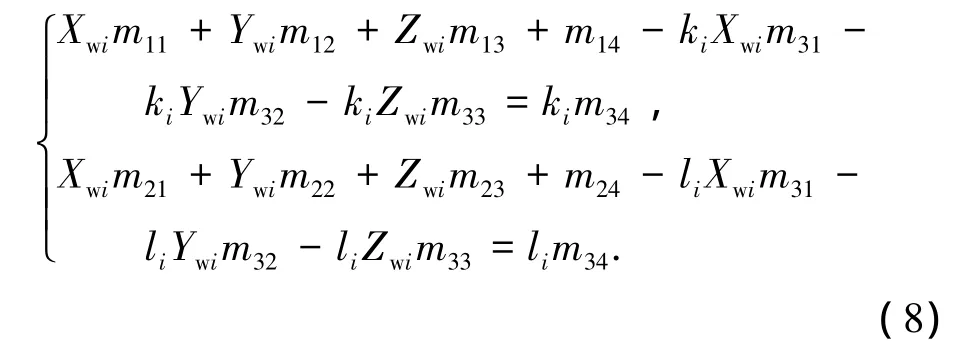
若在世界坐标系中取n个点,将会产生2n个方程,用矩阵形式写出这些方程如下:
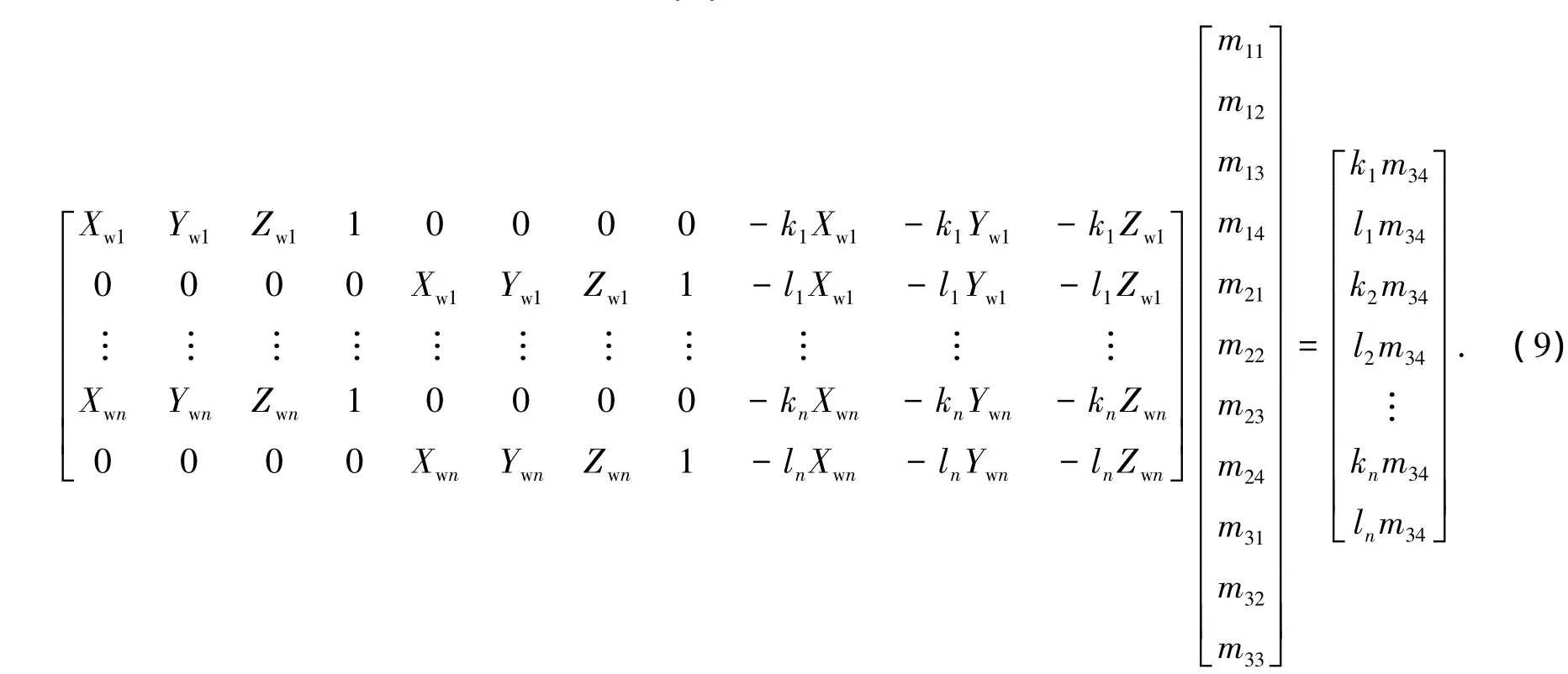
从式(9)可见,若已知世界坐标系中n个点的坐标,同时也知道各对应点在像素坐标系中的坐标,将式(9)两边同时除以m34(m34≠0)或取m34=1不影响方程的求解.式(9)可简写成
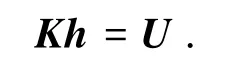
式中h,U分别为式(9)等号左侧向量和右侧向量除以m34后的向量.当2n>11时,上式成为一个超定方程,其最小二乘解可用下式表示:
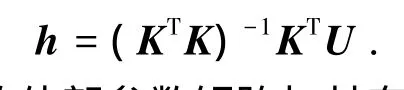
则数码相机的外部参数矩阵与其有如下关系:
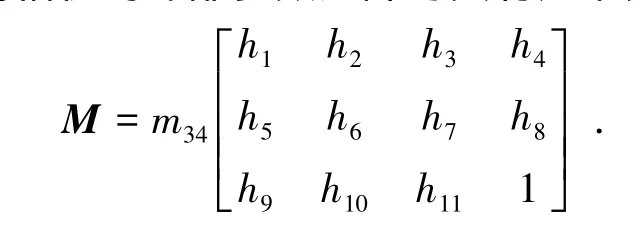
因R是正交矩阵,所以有
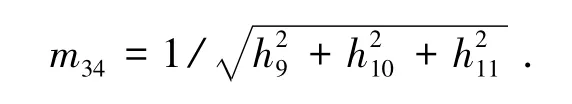
2 图像角点检测
在相机标定和三维重构中,如何准确地得到测点的像素坐标是摄像测量的关键.当测点的灰度值与背景灰度值相差较大时,利用角点检测算法可以准确地获得测点的像素坐标,本文采用Harris角点检测算法[17]对每一测点进行像素点提取.Harris角点检测算法将每一像素点的相似度抽象为
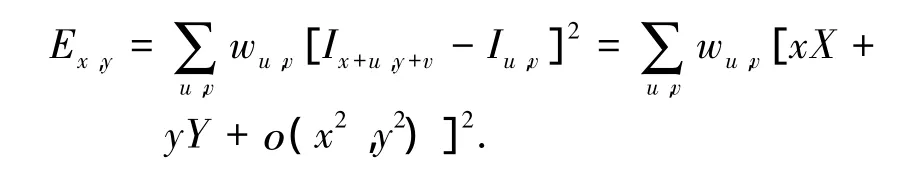
式中:Ⅰx,y表示像素点(x,y)的灰度值,x,y分别为像素点在u,v方向的变化量,且
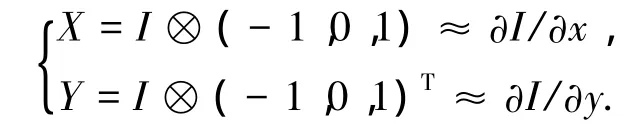
其中⊗为卷积算子.
因此,对于比较小的位移,E可表示为
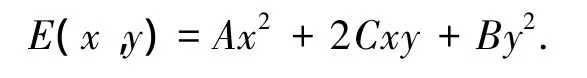
式中:
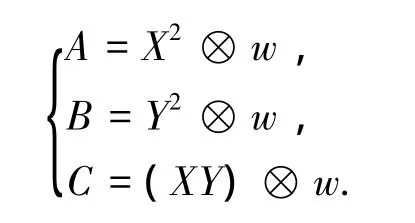
为了解决响应噪声的问题,算法引入一个平滑的高斯窗,通过对w的设定实现,其中
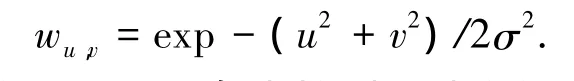
由式(9)Harris角点检测区域变化式,E可以通过矩阵形式表现出来:

式中:
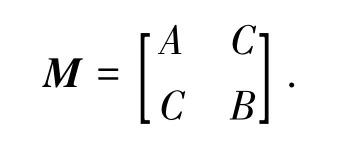
Harris算法的核心是计算矩阵M的特征值.M的两个特征值分别指示了该像素点在X,Y两个方向上的强度.若两个值都很大,则该像素点可认为是角点,只有一个较大而另一个较小时则认为是边缘点.在实际操作中,算法将M的两个特征值进行混合运算得出单一的强度值,并取局部强度值的最大点为特征点.
综上所述,利用数字摄像测量法测量在轨柔性结构振动的步骤可以总结如下:
1)分别对两个相机进行内外参数的标定;
2)选择合适的帧率对振动结构进行动态拍摄;
3)利用角点检测算法获得测点的像素坐标;
4)利用三维重构算法获得测点的世界坐标;
5)利用测点不同时刻的世界坐标得到其位移振动曲线.
3 星载天线模型实验
为验证上述方法的可行性,对一个星载柔性桁架天线模型进行了振动测试,并利用测试结果,采用特征系统实现法(ERA)[18]对其进行了模态辨识.
星载天线模型示意图如图2所示,反射面直径为750 mm,上下两层之间距离为150 mm,两层之间采用四根均匀分布直杆支撑,长度为150 mm.两根长支撑杆之间距离为50 mm,支撑杆长度为700 mm,所用材料直径均为3 mm,为了使其具有高柔性,低频的特性,采用了低刚度材料.在天线模型外圈测点上粘贴标志点便于图像处理,将天线支撑杆悬挂起来,两台高速摄像机一左一右放置于天线模型约1.5 m处,调节相机视场使其覆盖模型上所有测点,实验装置相对位置关系如图3所示.
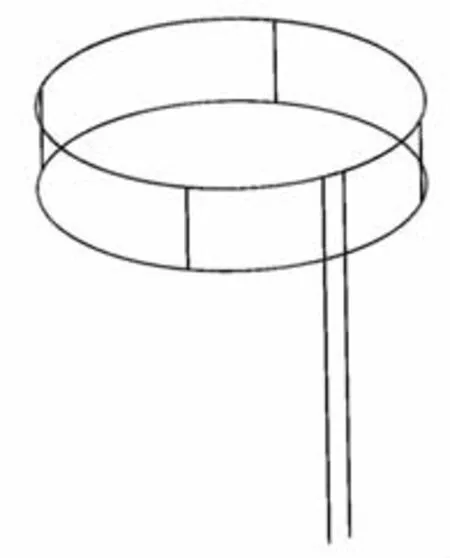
图2 星载天线模型

图3 双目摄像测量装置
实验步骤如下:
1)对相机进行标定时采用黑白相间的棋盘图,如图4所示.相机参数标定时采集标定板的多个位置的静态图片,找出每个图像中的角点,根据每个角点已知的物理坐标关系,利用1.2节中的标定方法得到相机的内外参数.

图4 相机内外参数标定
2)保持相机位置不变,设置相机触发模式与帧率,保证两个相机同步触发.本实验中,采用帧率150 fps进行图像采集,即对应采样频率为150 Hz.
3)给定天线模型一个初始位移,同时触发相机进行记录,直至振动衰减.
4)保存图像数据,用于分析处理.
利用相机标定方法求解出左侧相机内外参数矩阵分别为:

右侧相机内外参数矩阵分别为:
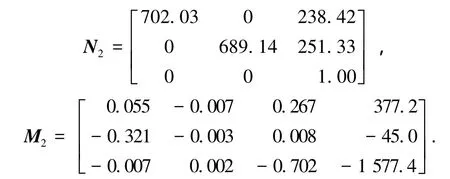
两个相机在某一时刻得到的图像如图5、图6所示.利用角点检测算法获得图中18个测点的像素坐标.以4号测点为例,两个相机图像中的像素位移曲线分别如图7~10所示.

图5 某一时刻左侧相机图像

图6 某一时刻右侧相机图像
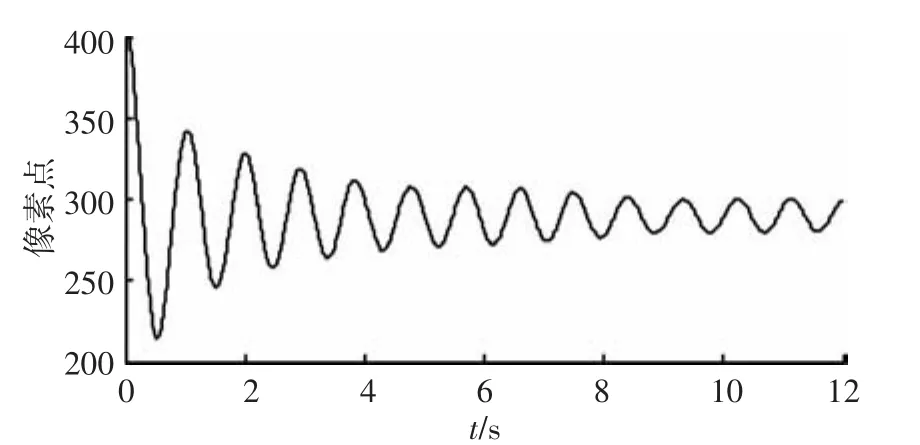
图7 左侧相机4号侧点X方向像素振动
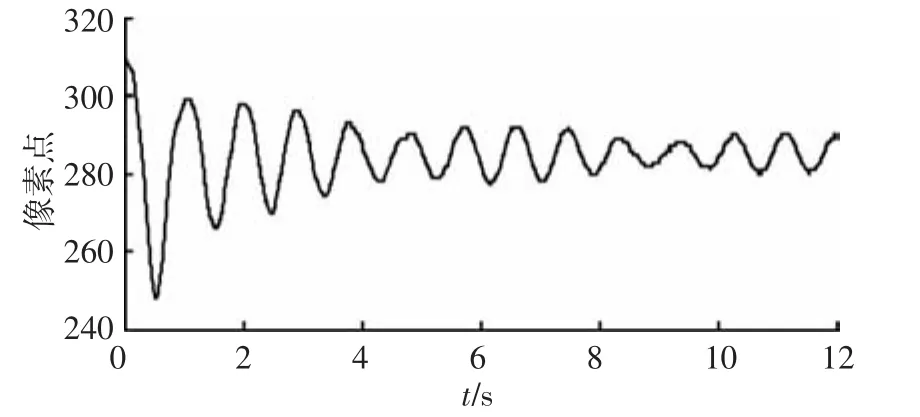
图8 左侧相机4号侧点Y方向像素振动
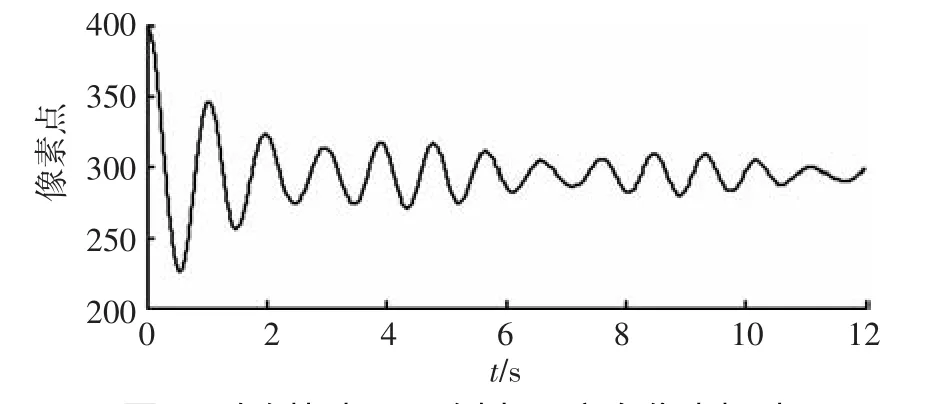
图9 右侧相机4号侧点X方向像素振动
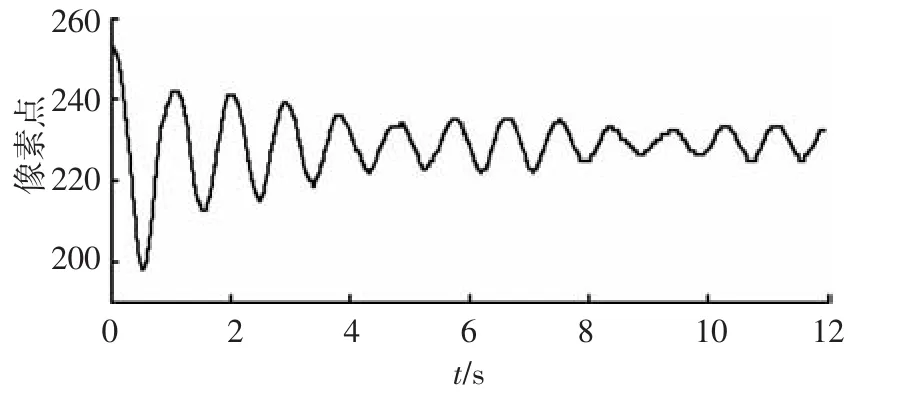
图10 右侧相机4号侧点Y方向像素振动
采用三维动态重构算法得到每个测点三自由度位移振动曲线,其中4号点三轴位移响应分别如图11~13所示.
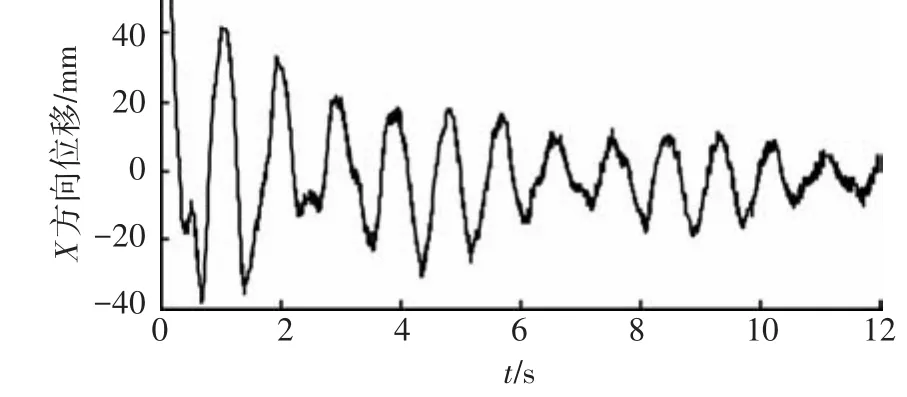
图11 4号测点X方向振动位移

图12 4号测点Y方向振动位移
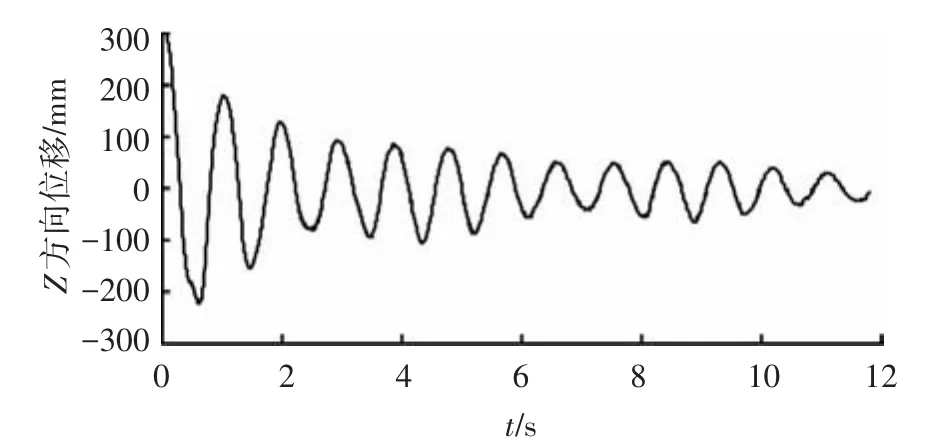
图13 4号测点Z方向振动位移
采用测得的天线模型上8个测点的振动响应,利用特征系统实现(ERA)法对天线模型进行模态参数辨识,得到其前5阶固有频率和阻尼比如表1所示,振型如图14(a)~14(e)所示,从图中可以看出,前三阶表现为反射器整体变形,是连接杆的弯曲和扭转所致,从第四阶开始出现了反射器本身的扭转变形.从表1中还可以看出,该天线模型固有频率较低,且第二、三阶频率接近.因此,采用摄像测量法能有效地辨识低频、密频在轨柔性结构的模态参数.
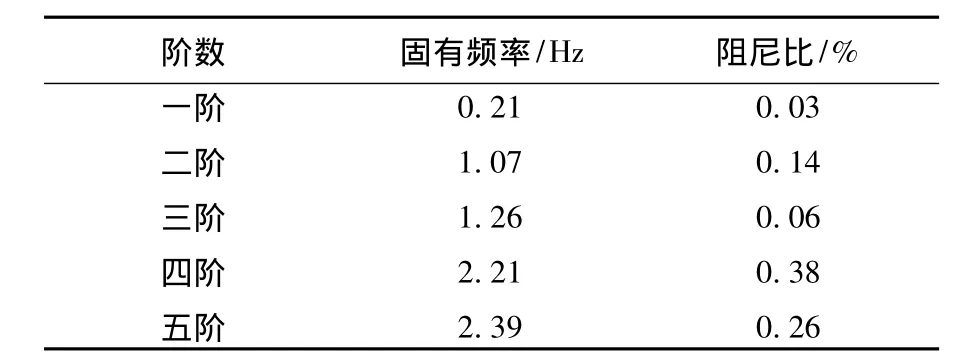
表1 天线模型ERA辨识结果
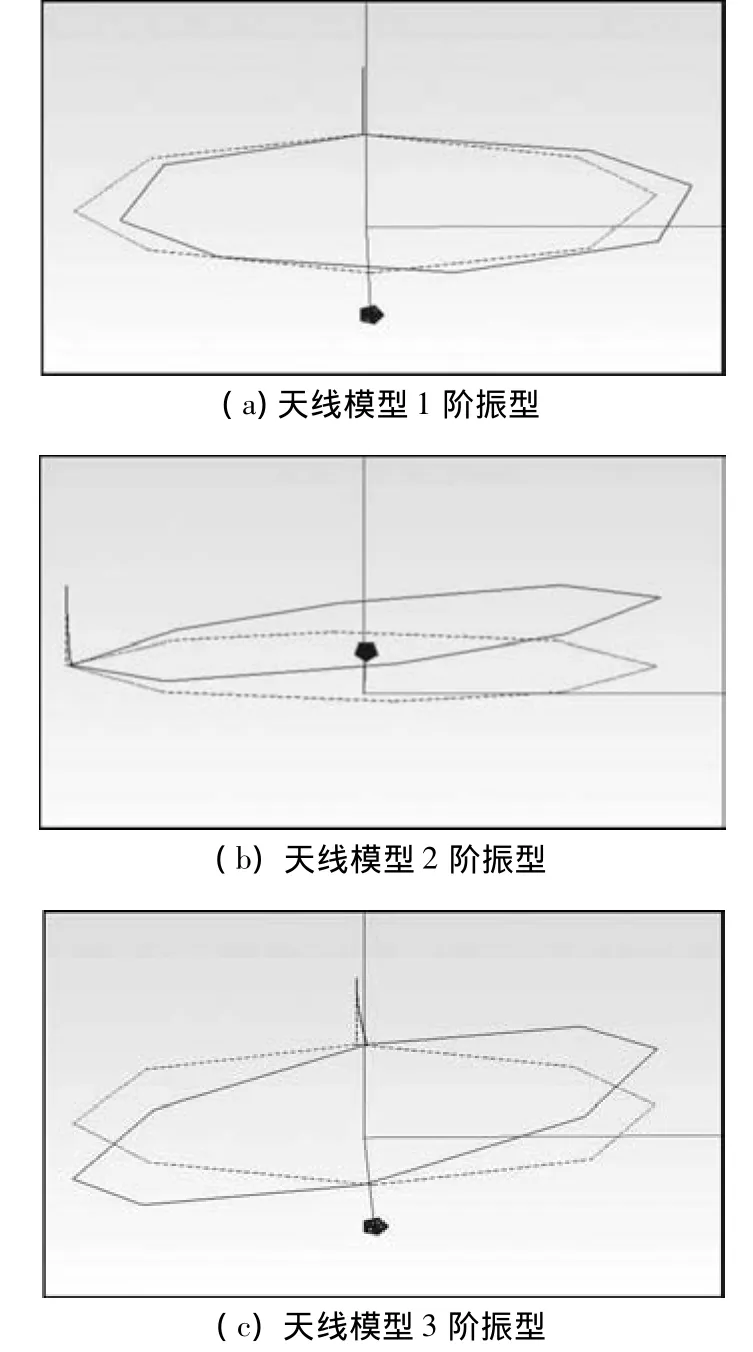
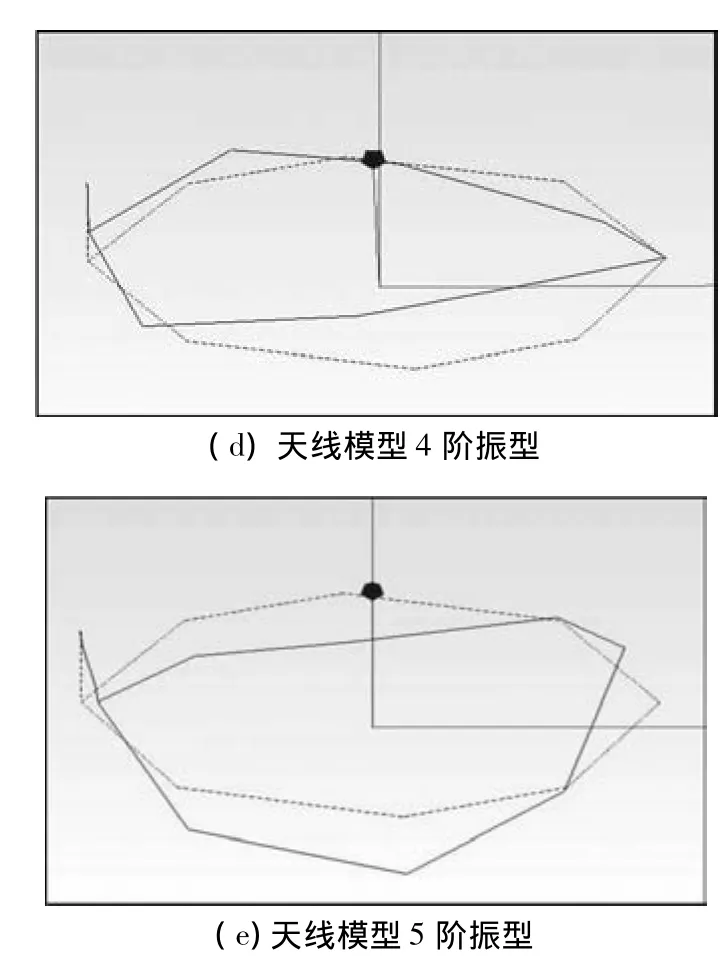
图14 天线模型前5阶振型
4 误差与精度分析
对天线进行模态分析的精度取决于成像系统分辨力、图像处理算法和辨识算法等众多因素.这里主要考虑摄像测量法特有的成像系统分辨力.成像系统对空间光学图像的最小细节的分辨能力称为成像分辨力,一般用图像物面分辨率或成像系统角分辨率来衡量.对于具体的测量对象,镜头焦距、光敏传感器芯片面积和成像物距决定了成像视场大小.当待测物体物距确定时,图像物面分辨率给出了图像中一个像素所代表的感兴趣的物面尺寸大小,因此这时用图像物面分辨率来衡量成像系统分辨率真具有直观性.而对于成像物距不定或变化的情况,对于镜头焦距一定的成像系统,其视场角是确定的,此时则适合用角分辨率来衡量成像系统分辨率.
每个像素所代表物面空间的尺寸称为图像物面分辨率.设拍摄视场大小为W×H,摄像机分辨率为M×N(称为硬件分辨率),则图像物面分辨率为
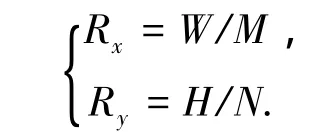
本次实验拍摄视场大小为100 mm×100 mm,分辨率为512×512,由上式可得图像物面分辨率为0.20 mm.角点检测算法提取像素点精度为1个像素,因此,本实验系统位移测量精度0.20/2=0.1 mm.为了提高拍摄精度,可以减小拍摄视场,或者提高相机分辨率,在相机与被测物距离受限时也可以通过长焦镜头减小视场.
测量中的误差主要由图像中存在的噪声引起,这种噪声不但影响测量过程,同时也会给标定带来误差.由于在轨和温度环境的复杂性,图像噪声会比地面试验中更大,需要采用合适的图像处理算法滤除以获得更精确地结果.
5 结语
针对大型柔性附件在轨模态辨识问题,提出了一种基于摄像测量的三维动态重构方法.首先对相机进行内外参数的标定,然后利用两个相机同时记录被测物的动态图像,通过角点检测算法获得测点的像素坐标,再根据三维重构算法得到测点的三维坐标,每一时刻测点三维坐标时间序列即是测点的三自由度位移振动曲线.利用天线模型和高速摄像机进行了地面验证实验,获得了模型上各个测点的振动曲线并据此辨识出了模型的前5阶模态参数,包括固有频率,阻尼比和振型.本文所述摄像测量法设备简单,可以根据实际测量要求选择合适的相机参数,以达到精度要求.实验表明,摄像测量法能有效地对大型柔性天线进行在轨模态辨识,且易于在轨实现,保证了卫星系统的可靠性,是一种具有良好应用前景的在轨响应测量方法.
[1]司宏伟,李东旭,陈卫东.大挠性航天桁架结构动力学及其主动控制研究进展[J].力学进展,2008,38(2):167-176.
[2]周舟,陆秋海,任革学,等.低密频太阳能帆板动力学参数在轨辨识和振动控制[J].工程力学,2004,21(3):84-89.
[3]黄文虎,曹登庆,韩增尧.航天器动力学与控制的研究进展与展望[J].力学进展,2012,42(4):367-394.
[4]张逸群,段宝岩,李团结.基于滤波的柔性可展开天线展开过程控制方法[J].机械工程学报,2012,48(3):180-188.
[5]游斌弟,赵志刚,李文博,等.空间热载荷作用下星载天线耦合动态影响分析[J].振动与冲击,2012,31(17):61-66.
[6]GENG L H,XIAO D Y,WANG Q,et al.Attitudecontrol model identification of on-orbit satellites actuated by reaction wheels[J].Acta Astronautica,2010,66(5):714-721.
[7]ANTHONY T,ANDERSEN G.On-orbit modal identification of the hubble space telescope[C]//American Control Conference, 1995. Proceedings of the IEEE.Piscataway:IEEE,1995,1:402-406.
[8]赵寿根,程伟,孙国江,等.航天器动力学特性参数在轨辨识技术[J].北京航空航天大学学报,2005,31(9):999-1003.
[9]党朝辉,项军华.超低轨卫星气动参数及转动惯量在轨实时辨识[J].上海航天,2012,29(5):20-24.
[10]CHANG C C,JI Y F.Flexible videogrammetric technique for three-dimensional structural vibration measurement[J].Journal of Engineering Mechanics,2007,133(6):656-664.
[11]BARROWS D A.Videogrammetric model deformation measurement technique for wind tunnel applications[C]//45th AIAA Aerospace Sciences Meeting and Exhitbit.Reston VA:AIAA,2007:AIAA 2007-1163.
[12]BURNER A W,LIU T.Videogrammetric model deformation measurement technique[J].Journal of Aircraft,2001,38(4):745-754.
[13]RYALL T G,FRASER C S.Determination of structural modes of vibration using digital photogrammetry[J].Journal of Aircraft,2002,39(1):114-119.
[14]GILBERT M G,WELCH S S.STS-74/MIR photogrammetric appendage structural dynamics experiment[R].Washington DC:NASA,1996.
[15]SAPP C A,DRAGG J L,SNYDER M W,et al.Photogrammetric assessment of the hubble space telescope solar arrays during the second servicing mission:final report[R].Washington DC:NASA,1998.
[16]ZHANG Z.A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.
[17]HARRIS C,STEPHENS M.A combined corner and edge detector[C]//Proceedings of the Fourth Alvey Vision Conference.Sheftield:University of Sheffield,1988:147-151.
[18]JUANG J N,PAPPA R S.An eigensystem realization algorithm for modal parameter identification and model reduction[J].Journal of Guidance, Control, and Dynamics,1985,8(5):620-627.

