人头面部轮廓数学模型的研究

吴伟国，闫云雪

（哈尔滨工业大学机电工程学院，150001哈尔滨）

人头面部轮廓数学模型的研究

吴伟国，闫云雪

（哈尔滨工业大学机电工程学院，150001哈尔滨）

针对现有图像处理技术中提取人脸轮廓线光滑性差的问题，提出一种人头面部轮廓的分段建模方法.通过轮廓特征点定义和轮廓分段，采用超椭圆、圆弧和抛物线等曲线建立了人头面部轮廓数学模型，选取100组5种脸型的真实人头面图像经图像处理及优化后，用获得的轮廓样本参数对模型进行验证.结果表明，对于任一样本，该模型在进行参数优化后都能保证模型平均误差在1.2%以下，最大误差在2.6%以下，验证了该模型的有效性和普适性.提出了基于该模型的脸型判定方法，给出了各类脸型的模型参数范围.

人头面部轮廓；数学模型；超椭圆曲线；脸型判定方法

人脸轮廓是人脸重要的特征信息，其在各个领域的应用也越来越广泛.文献［1-3］针对下颌轮廓线的特点，研究了下颌轮廓线的提取与分类，利用抛物线模型和折线模型建立下颌形状模板，并将其运用于人脸识别系统，提高了人脸识别的正确率和识别速度.在人脸三维建模中，精确的面部轮廓线是模型建立的必要前提［4］.同时，人脸轮廓线在人脸检测［5-6］、人脸表情动画［7-8］以及面部整容医学等方面也有着广泛的应用，相比于通过对人脸皮肤颜色过滤的方法［9］更能够反映面部的真实特征，这使得对于面部轮廓线获得方法的研究成为国内外众多学者的研究热点.目前，常用的轮廓线获得方法有：可变形模板，该方法对面部器官轮廓的提取效果较好，但存在着初始值定位困难且计算复杂的问题；活动轮廓模型（Snake模型）［10-12］，该方法能够用于任意形状轮廓线的精确提取，但受参数初值的影响大，计算繁琐也制约了该方法的应用.此外，隐式的水平集、Cabor小波变换、Hough变换等方法也用于人脸轮廓的检测与提取，但得到的轮廓线连续性和光滑性较差；近几年，基于Snake模型的改进算法逐渐被学者提出，效果较好的是基于PGVF Snake模型［13］的人脸轮廓提取方法，该方法通过将梯度矢量场引入外部能量项，克服了传统Snake模型的缺点，能够较快速准确地提取人脸轮廓，提取出的人脸轮廓效果如图1所示.从图中可以看出，虽然提取出的人脸轮廓线逼近于真实人脸轮廓线，但轮廓曲线光滑性差，其精确性也有待提高.

图1 基于PGVF Snake模型提取的轮廓线

上述几种方法提取出的人脸轮廓线都存在以下共性问题：当照片质量有缺陷时，得到的轮廓线会出现较大的拐点，导致轮廓的精确性下降；得到的轮廓线连续性、光滑性较差且无法对其进行局部调整；轮廓线的存储和再现方式依赖于大量离散点数据信息，增加了人脸轮廓数据库建立和人像比对的复杂性.

为解决以上问题，同时旨在将人脸轮廓应用于脸型可变仿人头像机器人研究当中，本文对人头面部轮廓数学模型的建立进行了研究，并给出了具体的数学表达.

1 人头面部轮廓特征点的选取

人头面部的几何结构复杂，存在很大的差异，但人头面部的轮廓形态却存在一定的规律，其中顶骨的弯曲形状决定了头部轮廓线的形态；额骨、颧骨、上颌骨以及下颌骨等颅面骨基本上决定了面部轮廓线形态；面部肌肉组织的附着赋予了人头面部轮廓线光滑这一特性.

通过对人脸结构形态进行分析，定义头顶点v、颅侧点eu、上颌骨圆弧起点g1、下颌骨圆弧终点g2、颏下点gn作为人头面部轮廓特征点（其中头顶点v、颅侧点eu和颏下点gn为人体测量学中定义的骨性标志点），各特征点具体位置如图2所示．

各特征点在人头面部轮廓中的意义为：头顶点v为法兰克福平面（法兰克福平面是由左右侧耳门上点（po）和左侧眼眶下缘点（or）3个点所确定的一个平面，也称眼耳平面，如图3所示）以上，距离法兰克福平面最远的点；颅侧点eu为位于顶骨区域内以及颞侧面最突出的点，两颅侧点间宽表征头面轮廓最大宽；g1点为下颌骨圆弧起点；g2点为下颌骨圆弧终点；颏下点gn为法兰克福平面以下，距离法兰克福平面最远的点，和头顶点v共同表征头面轮廓最大长度．可以看出，这些特征点的位置结合各点依次连接的方式决定了人头面部轮廓的形状．

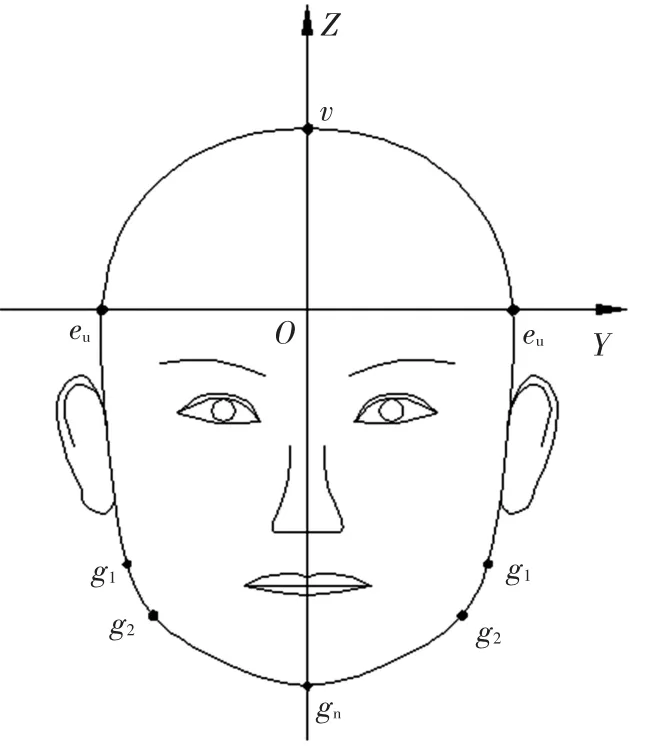
图2 特征点位置及头面部正面坐标系

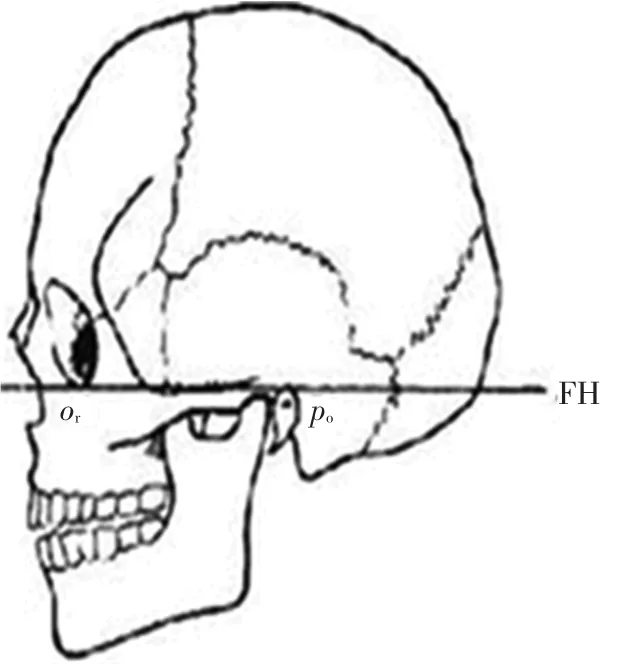
图3 法兰克福平面示意图

2 人头面部轮廓数学模型的建立

人头面部轮廓的多样性和光滑性要求建立的数学模型具有普适性，并要保证模型曲线光滑连续，同时为了便于不同脸型之间的迁移，在保证模型有效性的前提下其参数应尽量少，本文采用分段函数建立该数学模型.

坐标系的建立方式如图2所示，以左右颅侧点连线和正中矢状面（将人头部分为左右对等的面）的交点作为原点O建立直角坐标系，以两颅侧点连线作为Y轴，向右为正；Z轴位于正中矢状面上，垂直于Y轴，向上为正；X轴符合右手定则．

由于人头面部结构左右对称，这里只阐述右半部分头面轮廓的数学模型建立方法．首先，根据特征点将人头面部轮廓进行分段，分段情况以及各段采取的模型曲线为：v～eu段，超椭圆曲线；eu～g1段，椭圆曲线；g2～gn段，抛物线；g1～g2段：圆弧曲线，该圆弧为eu～g1段椭圆曲线和g2～gn段抛物线的相切圆弧．

设各特征点坐标为：v点（0，b），eu点（a，0），g1点（m，n），g2点（g，h），gn点（0，B）．则右半部分人头面部轮廓的数学模型为

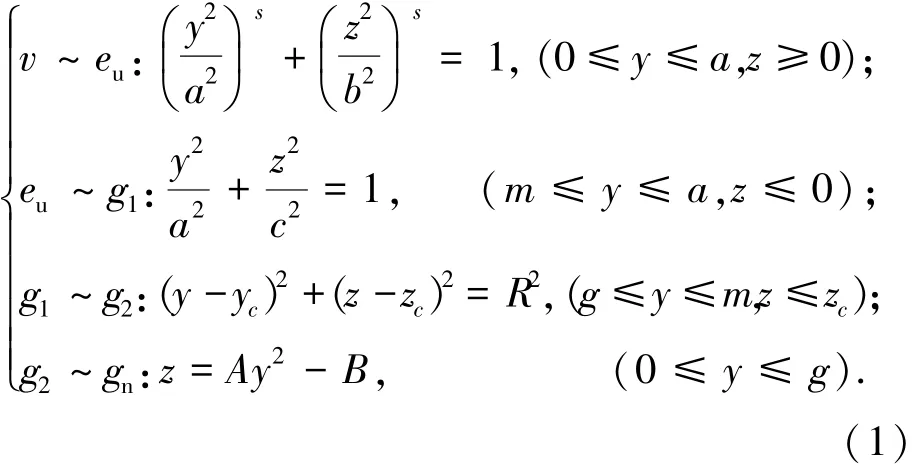
式中：

当a≥b时，a为超椭圆长半轴，当a＜b时，a为超椭圆短半轴；s为超椭圆指数；c、d分别为椭圆长半轴、短半轴，（yc，zc）为椭圆曲线和抛物线的相切圆弧圆心坐标．

由式（1）可知，a、b、s、c、m、g，R这7个独立的参数就足以控制模型曲线形状．为便于确定参数范围，将m、g分别表示成椭圆参数方程以及圆参数方程中的坐标形式：m＝acos θ，

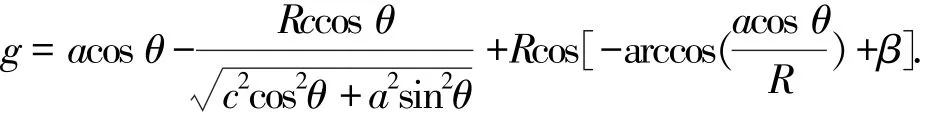
则最终的模型参数为a、b、s、c、θ、β、R，对这7个独立参数进行优化即可得到任一特定人头面部轮廓的数学模型．通过计算该数学模型在连接点处的左右导数，能够证明该模型曲线光滑，这里不做赘述．

3 人头面部轮廓模型参数的优化

由于本文建立的人头面部轮廓数学模型为通用模型，对于任一给定的真实人头面部轮廓，为得到其特定的数学模型并使模型曲线与真实头面轮廓的误差最小，需要对模型参数进行优化.

3.1 模型误差的定义

采用人体测量学的方法对被测量者头全高进行测量，测量时应使被测量者保持直立姿势，两眼向前平视，头部位于眼耳平面，设测得的头全高为H；利用数码设备获取被测量者的正面头部照片，测得图片上头全高为h，则照片上人头面部轮廓经图像处理后进行比例放大即得到真实人头面部轮廓线数据点，其中，比例因子k＝H／h；最后建立该真实轮廓线的数学模型，并将得到的模型曲线定义为理论轮廓线．

本文以样本理论轮廓线上数据点和真实轮廓线上对应数据点间的相对距离衡量模型误差，定义各对数据点相对距离的平均值和最大值为模型平均误差和最大误差．数据点的选取方法如图4所示，首先将理论轮廓线和真实轮廓线均置于所建立的模型坐标系中，以原点O为中心，z≥0区域的曲线，每隔γ1取数据点，z＜0区域的曲线，每隔γ2取数据点，真实轮廓线和理论轮廓线上各取n个数据点．

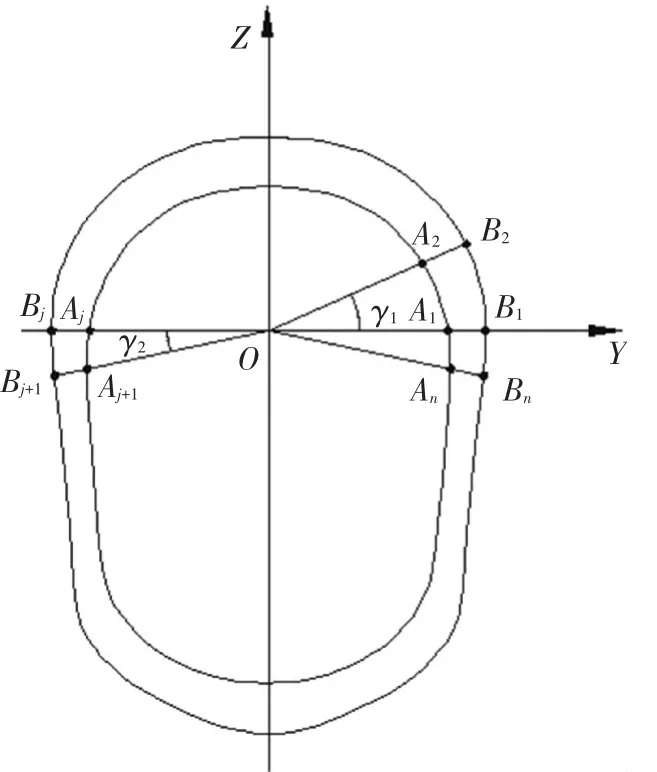
图4 误差计算中数据点的选取

设真实轮廓线数据点为Ai（i＝1，2，…，n），Ai坐标为（yi，zi）；理论轮廓线数据点为Bi（i＝1，2，…，n），Bi坐标为（y0i，z0i）；则数据点Bi与数据点Ai的相对距离平均值为

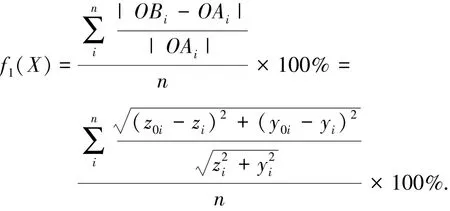
数据点相对距离最大值为

3.2 模型参数的优化

为了可靠、全面地说明模型的有效性，以理论轮廓线数据点与真实轮廓线上对应数据点的相对距离平均值和最大值的加权和作为优化设计的目标函数，由此得到优化设计的数学模型.

1）设计变量：

2）目标函数：

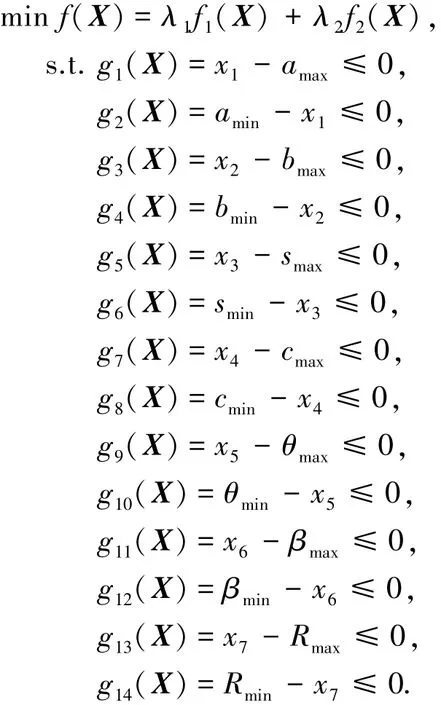
式中：λ1、λ2为加权系数，λ1＋λ2＝1，由于平均值反映综合误差，最大值反映局部误差，取λ1，λ2分别为0.6，0.4．

根据《成年人头面部尺寸》［14］以及人体测量学中上述特征点在人头面部的分布原则，得到：amax＝90 mm，bmax＝90 mm，smax＝4，cmax＝250 mm，θmax＝0，βmax＝0；Rmax＝30 mm，amin＝65 mm，bmin＝70 mm，smin＝0．7，cmin＝150 mm，θmin＝-2 rad，βmin＝-1 rad，Rmin＝0．

对该优化模型分析表明，其属于多峰函数.遗传算法能够同时对搜索空间中的多个解进行评估［15］，具有较好的全局搜索性能，对于非线性、多峰值函数能以很大的概率找到全局最优解；因此，本文利用遗传算法求取模型参数最优解.

3.3 算例验证

将100组汉族成人真实头面轮廓作为算例样本，其中男女比例为1∶1，包含圆形脸等5种脸型类别，各类型均为20组，为使数据点充足且分布均匀，取γ1＝6°，γ2＝3°，即n＝90.图5为对心形脸类别中随机抽取的一组样本进行头面轮廓建模得到的模型效果图.图5（a）为该样本正面照片；图5（b）为样本真实轮廓线和理论轮廓线对比图；图5（c）给出了具体的真实轮廓线和理论轮廓线上各对数据点的相对距离及模型误差.

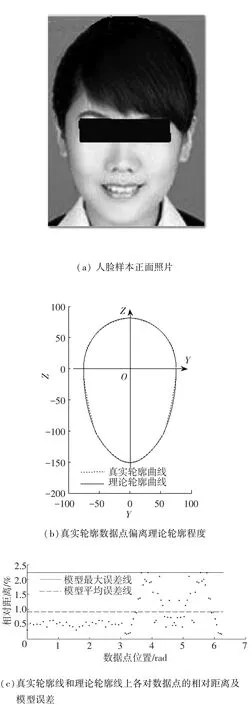
图5 心形脸类别中一组样本头面轮廓建模效果

表1给出了对其他脸型样本中随机抽取的样本进行头面轮廓建模得到模型参数、各对数据点的相对距离和模型误差.通过计算100组算例样本的模型误差可知，对于其中任一样本，该模型在进行参数优化后都能保证模型平均误差在1.2%以下，最大误差在2.6%以下，验证了该数学模型的有效性和普适性.

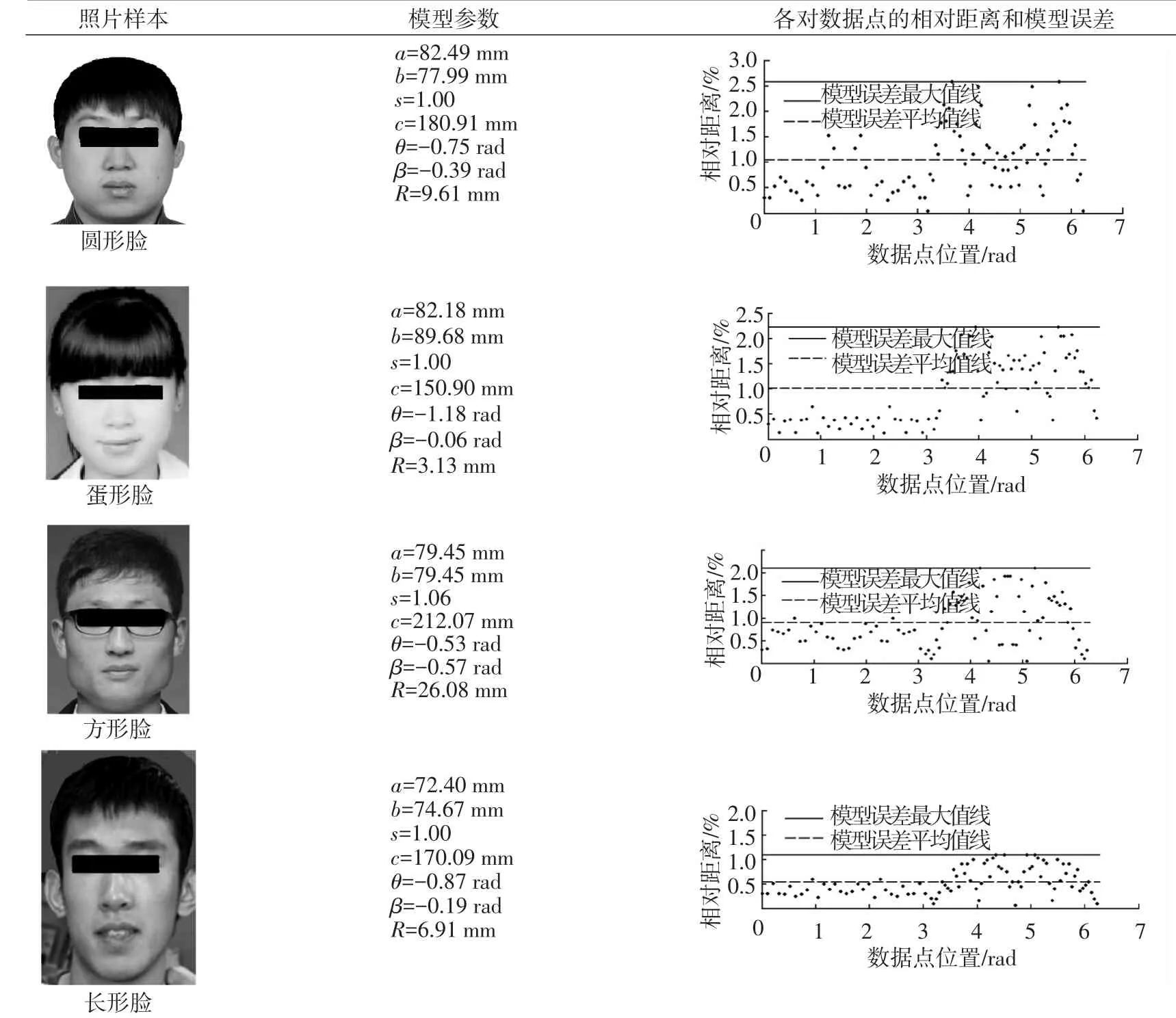
表1 模型参数、各对数据点的相对距离和模型误差

4 各类脸型模型参数范围的确定

4.1 曲线相似性的定义

为了使脸型的判定有明确的衡量标准，给出本文对曲线相似性的定义：

设有曲线M1N1、M2N2，将这两条曲线置于同一直角坐标系中，连接点M1、M2与点N1、N2，线段M2M1和N2N1的延长线交于点O．如图6所示，以O点为圆心，以γ为间隔在曲线M1N1上取点P1，P2，…，Pn-2，得到集合P＝｛M1，P1，P2，…，Pn-2，N1｝；在曲线M2N2上取点Q1，Q2，…，Qn-2，得到集合Q＝｛M2，Q1，Q2，…，Qn-2，N2｝．

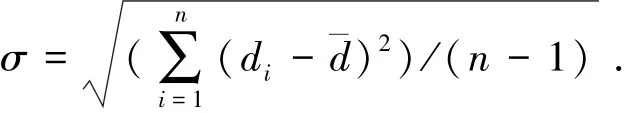
图6 数据点的获取方法

4.2 脸型判定方法的研究

基于先验知识可知，脸型可以分为圆形脸、方形脸、长形脸、蛋形脸以及心形脸，选出各类脸型中具有代表性的人脸样本并将样本真实头面轮廓曲线作为标准脸型模板，如图7所示.

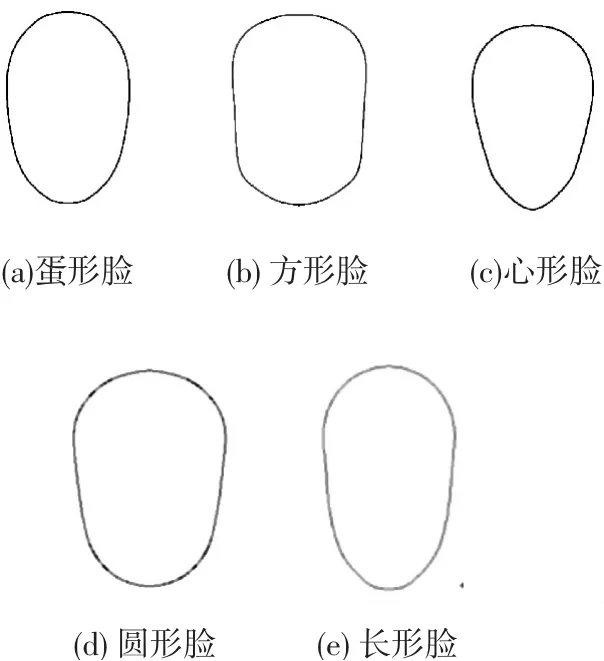
图7 标准脸型模板

根据曲线相似性定义，分别计算待分类人脸样本真实头面轮廓和5种标准脸型曲线的均方差，设均方差分别为σ1、σ2、σ3、σ4、σ5，则σmin对应的模板类型即该人脸样本对应的脸型类别，其中σmin＝min｛σ1，σ2，σ3，σ4，σ5｝．因为头顶轮廓对脸型没有影响，故只对颅测点以下曲线进行均方差的计算．

利用上述方法对100组人脸样本进行分类，限于篇幅这里只给出部分人脸样本的分类结果，如图8所示.

图8 部分样本分类结果

最后通过10个人对这100组样本进行脸型类别认知实验，认知结果和采用本文的脸型分类方法得到的分类结果相似率达到85%以上，验证了该分类方法的有效性.表2为认知实验中部分样本的认知结果.

表2 识别实验中部分样本的识别结果

4.3 各类脸型模型参数范围的确定

对100组脸型进行分类后，建立各类脸型样本头面轮廓的数学模型，对模型参数范围进行总结，为以后对脸型可变仿人头像机器人的研究提供理论基础，脸型与模型参数范围的对应关系见表3所示.

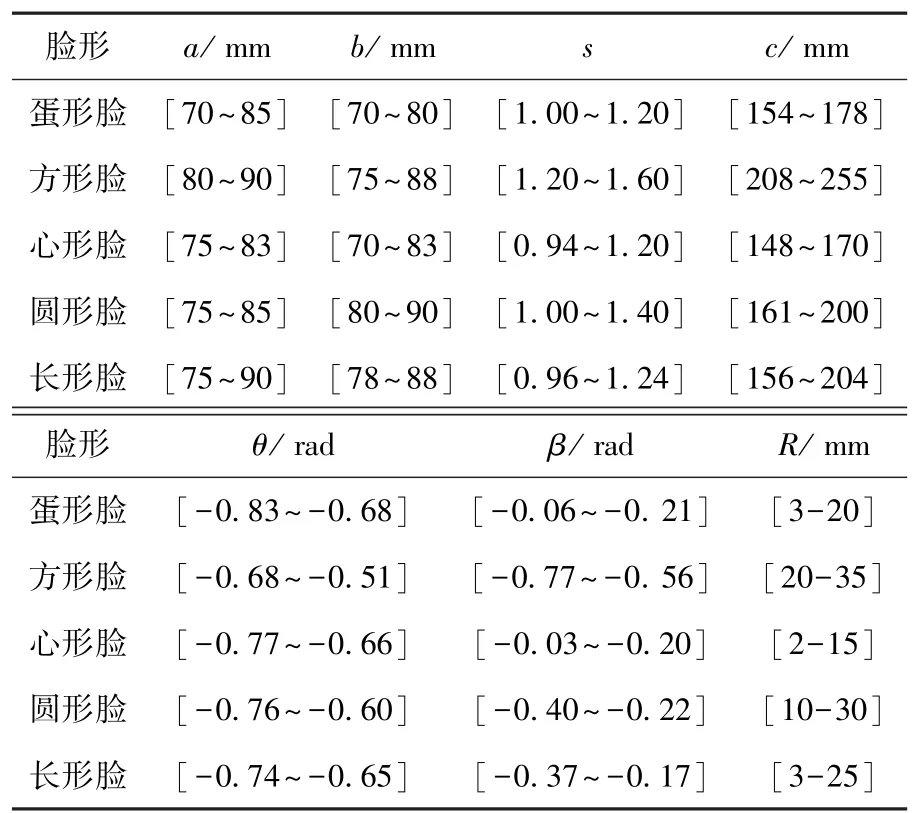
表3 各类脸型对应的模型参数范围

5 结 论

1）利用超椭圆曲线、椭圆曲线、圆弧曲线以及抛物线建立了人头面部轮廓的具有7个独立参数的数学模型，从而实现了将人脸轮廓大量离散点的存储转化为7个独立参数存储，简化人脸数据库建立的复杂性.

2）以理论轮廓线数据点Ai相对真实轮廓线上对应数据点Bi的偏离距离平均值和最大值为优化目标对模型参数进行优化，利用遗传算法求取模型参数最优解，从而实现特定人脸轮廓模型的建立.

3）选取100组真实人头面轮廓样本对模型进行验证，结果表明，对于任一样本，该模型在进行参数优化后都能保证模型平均误差在1.2%以下，最大误差在2.6%以下，验证了该数学模型的有效性和普适性.

4）当人脸正面照片存在质量缺陷或部分遮挡时，只需提取出真实轮廓有效的特征点位置数据，同样可以得到连续光滑的人头面轮廓曲线，因此能够弥补图像处理方法中对人脸轮廓提取的不足.

5）提出一种新的脸型分类方法，确定出各类脸型模型参数范围，拓宽了人头面轮廓在仿人头像机器人等领域的应用，为人脸轮廓线的提取、人脸识别、脸型迁移以及人脸三维建模的进一步研究提供了基础.

致 谢

向提供头面部图像并接受头全高测量的机械设计系研究生们致以衷心的感谢！

［1］王俊艳，苏光大，林行刚.用于人脸识别的下颌轮廓线分类方法［J］.光电子·激光，2005，16（11）：1368-1372.

［2］GU Hua，CHENG Du.Fuzzy and ISODATA classification of facecontours［C］／／Proceedingsofthe2004 InternationalConferenceonMachineLearningand Cybernetics.Piscataway：IEEE Press，2004：3568-3573.

［3］王俊艳，苏光大.基于下颌轮廓线的人脸分类方法［J］.红外与激光工程，2004，33（2）：159-163.

［4］GOTO T，LEE W S，MAGNENAT⁃THALMANN N. Facial feature extraction for quick 3D face modeling［J］.Signal Processing：Image Communication，2002， 17（3）：243-259.

［5］方昱春，王蕴红，谭铁牛.融合人脸轮廓和区域信息改进人脸检测［J］.计算机学报，2004，27（4）：482-491.

［6］HSU C Y，WANG H F，WANG H C，et al.Automatic extraction of face contours in images and videos［J］. Future Generation Computer Systems，2012，28（1）：322-335.

［7］王翔宇，肖俊，潘红.表演驱动的矢量化二维表情动画［J］.计算机辅助设计与图形学学报，2012，24（5）：598-604.

［8］YANG Yang，ZHENG Nanning，LIU Yuehu，et al. Expression transfer for facial sketch animation［J］. Signal Processing，2011，91（11）：2465-2477.

［9］ORTEGA G D，PERNAS F J，ZARZUELA M M，et al. Real-time hands，face and facial features detection and tracking：Application to cognitive rehabilitation tests monitoring［J］.Journal of Network and Computer Applications，2010，33（4）：447-466.

［10］PERLIBAKAS V.Automatical detection of face features and exact face contour［J］.Pattern Recognition Letters，2003，24（16）：2977-2985.

［11］BING X，WEI Y，CHAREONSAK C.Face contour extraction using Snake［C］／／2004 IEEE International WorkshoponBiomedicalCircuitsandSystems. Piscataway：IEEE Press，2004：S3.2-5-S3.2-8.

［12］FANG H，KIM S H，JANG J W.A snake algorithm for automatically tracking multiple objects［C］／／2011 18th IEEE International Conference on Image Processing. Piscataway：IEEE Press，2011：469-472.

［13］HSU C Y，WANG H F，WANG H C，et al.Automatic extraction of face contours［C］／／Proceedings of The 2010 International Joint Conference on Neural Networks（IJCNN）.Piscataway：IEEE Press，2010：1-8.

［14］国家标准化管理委员会.GB／T 2428-1998成年人头面部尺［S］.北京：中国标准出版社，1998.

［15］DEB K，PRATAP A，AGAWAL S，et al.A fast and elitist multiobjective genetic algorithm：NSGA⁃II［J］. IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197.

（编辑 杨 波）

Research on mathematical model for human head⁃face contour

WU Weiguo，YAN Yunxue

（School of Mechatronics Engineering，Harbin Institute of Technology，150001 Harbin，China）

Face contour extracted by most existing extraction technology has the problem of non⁃smooth.Aimed at this situation，an segmentation modeling method for head⁃face contour is proposed.The piecewise function model is established using hyperelliptic curve，elliptic curve，circular curve and parabolic curve according to points definition and segmentation of contour.Contour sample＇s parameters obtained from the processing and optimization of 100 real human head⁃face images which contains five kinds of face verify the effectiveness and universality of the model.The result shows that the average error is under 1.2%and the maximum error is under 2.6%for each sample after optimizing the model.Finally the range of model parameters corresponding to each type of face is given by face shape classification based on the mathematical model.

head⁃face contour；mathematical model；hyperelliptic curve；face shape classification

TP391

：A

：0367-6234（2014）11-0030-07

2014-06-06.

国家高技术研究发展计划（2006AA04Z201，2012AA041601）.

吴伟国（1966—），男，教授，博士生导师.

吴伟国，wuwg＠hit.edu.cn.