固定序Bellman⁃Ford算法的一个改进

韩伟一

（哈尔滨工业大学经济与管理学院，150001哈尔滨）

固定序Bellman⁃Ford算法的一个改进

韩伟一

（哈尔滨工业大学经济与管理学院，150001哈尔滨）

通过对固定序Bellman⁃Ford算法进行修正，获得了一种求解边数不大于k的最短路问题的新算法．相对于原始算法，修正后的算法通过改变点的标号过程，使得在第k次迭代后每一条路径的边数均不超过k．新算法被证明是正确的，它的计算复杂性为O（km）．实验表明，在大规模情形下，相对于修正的先进先出算法，该算法具有显著的竞争优势.

算法；Bellman⁃Ford算法；先进先出；固定序；最短路问题

自1958年以来，Bellman⁃Ford算法一直被公认为是求解负权最短路问题最好的强多项式算法，它的研究历程可概括为3个发展阶段［1-3］：第1阶段，动态规划模式阶段，即原始的Bellman⁃Ford算法；第2阶段，基本改进阶段，在第1阶段的每次迭代中所有点都要参与计算，而在第2阶段中只有在上次迭代中距离标号改变的点才参与下一次迭代，从而使得计算效率显著提高，迭代次数明显减少［4-8］；第3阶段，加速技术阶段，主要体现为上次迭代中距离标号改变的点并不全部参与下一轮迭代计算，因而还可进一步提高计算效率.第3阶段的算法一般以第2阶段的算法为基础，因而第2阶段的算法也称为Bellman⁃Ford算法的基本改进算法.目前，主要有5类基本改进算法，即先进先出算法［4，8］、后进先出算法［8］、Yen算法［9］、快速算法［10］和固定序算法［1-2］等.第3阶段的主要工作有1993年Goldberg等［11］提出的拓扑序技术，1981年Tarjan［12］提出的装配子树技术，以及1985年Glover等［13-14］提出的门槛技术等，1996年Cherkassky等［4，8］提出的父点技术等.需要指出的是，尽管第2、3阶段的算法都具有很高的效率，但由于最短路径中的边数可能会多于k条，因而均不能解决边数不大于k的最短路问题（或边数≤k的最短路问题），为此文献［2］对先进先出算法进行了修正．本文将对固定序算法进行修正，使得修正后的算法能够解决有边数限制的最短路问题，并将该算法与已有的先进先出算法进行比较，用实验说明它在大规模情形下具有显著的竞争优势．

1 固定序算法及其修正

对于一个具有n个点、m条边的有向图G（V，E），n个点分别编号为1，2，…，n，且规定点1为源点，用w（i，j）表示有向边（i，j）的权．定义d（i）为点i的距离标号，h为迭代次数．固定序算法如下：

Step 1 初始化.令d（1）＝0，d（i）＝＋∞，2≤i≤n．把点1加入集合A．对h赋值为1．

Step 2 在第h次迭代中，按照编号顺序对A中的各点i进行计算

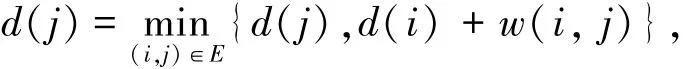
如果d（j）变小，则当j∉A时，把点j加入集合A．从集合A中去除点i．

Step 3 如果集合A为空集，则算法结束，d（i）就是从点1到点i的最短距离；当集合A非空且h＝n-1时，可判定存在负循环，算法结束；当集合A非空且h＜n-1时，执行Step 4.

Step 4 令h＝h＋1，转到Step 2.

尽管固定序算法在求解负权最短路问题上具有较高的计算效率，但由于求得的是最短路径，而最短路径中可能会多于k条边，因而它也无法直接求解边数≤k的最短路问题，必须对它加以修正．

在对固定序算法修正以前，需要引入一些新的定义和符号：1）定义d0（i）为上次迭代完成后点i的距离标号；2）在修正的算法中，定义集合A为上轮迭代中距离标号变小的点的集合，定义集合B为本轮迭代中距离变小的点的集合．修正后的固定序算法如下：

Step 1 初始化.令d（1）＝0，d（i）＝＋∞，2≤i≤n，把点1加入集合A．迭代次数h赋初值为1，则第0次迭代的距离标号分别为

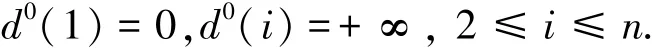
Step 2 在第h次迭代中，按照编号顺序对A中的各点i进行计算

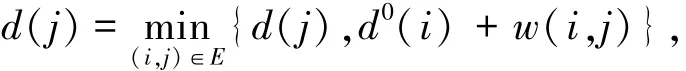
如果d（j）＜d0（j），且当点j∉B时，把点j加入集合B．从集合A中去除点i．

Step 3 如果集合B为空集或h＝k时，则算法结束，d（i）就是从点1到点i的最短距离；当集合B非空且h＜k时，执行Step 4.

Step 4 清空集合A，并把集合B中的元素转到集合A，再清空集合B，同时对任意的点i（1≤i≤n），令

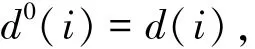
再令h＝h＋1，转到Step 2.

2 修正的先进先出算法

文献［2］对基于先进先出序的Bellman⁃Ford算法进行了修正，使之能够解决边数不大于k的最短路问题，特称为修正的先进先出算法.作为Bellman⁃Ford算法的一种基本改进算法，先进先出算法被公认为是解决负权最短路问题最快、最有影响力的算法，第3阶段的加速算法都是以它为基础进行改进的.在文献［2］中，修正的先进先出算法不仅可以求解边数≤k的最短路问题，而且显示出了卓越的计算效率，相对于原始的Bellman⁃Ford算法效率可提高近30倍.需要指出的是，原始的Bellman⁃Ford算法可以求解边数≤k的最短路问题，但第2、3阶段的改进算法均不可以.

修正的先进先出算法仍然采用相应固定序算法的问题描述和符号，算法如下：

Step 1 初始化．令d（1）＝0，d（i）＝＋∞，2≤i≤n，把点1加入集合A．迭代次数h赋初值为1，则第0次迭代的距离标号分别为

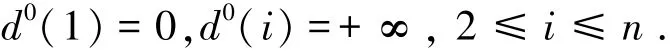
Step 2 在第h次迭代中，按照进入顺序对A中的各点i进行计算

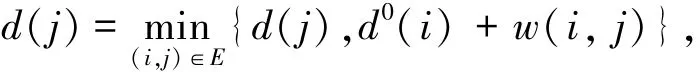
如果d（j）＜d0（j），且当点j∉B时，把点j加入集合B．从集合A中去除点i．

Step 3 如果集合B为空集或h＝k时，则算法结束，d（i）就是从点1到点i的最短距离；当集合B非空且h＜k时，执行Step 4.

Step 4 清空集合A，并把集合B中的元素转到集合A，再清空集合B，同时对任意的点i（1≤i≤n），令

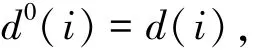
再令h＝h＋1，转到Step 2.

需要指出的是，本文对文献［2］中的修正的先进先出算法的表述错误进行了纠正，即把d（j）＝修正为d（j）＝

比较两种修正算法，可以看出两种算法仅仅在Step 2有微小的差别，也就是修正的先进先出算法参与计算的点按照先进先出的顺序，而修正的固定序算法则按照事先给定的编号顺序.两个算法满足如下定理.

定理1 对于同一个问题，修正的先进先出算法和修正的固定序算法不仅具有相同的迭代次数，而且每一次迭代使用的集合A和迭代后形成的集合B也是相同的．

证明 两个算法仅仅在Step 2存在一定的差别，其他步骤都是一样的.在Step 2中，修正的先进先出算法按照先进先出的顺序对A中的点进行计算，而修正的固定序算法按照给定的顺序对A中的点进行计算．如果每一次迭代使用的集合A是相同的，而且得到的计算结果也是相同的，那么两个算法无疑具有同样的迭代次数．

定理1间接说明，本文的算法确实可以求解边数≤k的最短路问题．也进一步表明，修正的先进先出算法和修正的固定序算法应该具有同样的计算复杂度．由文献［2］，有如下引理．

引理1 算法在k次迭代后，如果d（i）＜＋∞，那么可得到从点1到点i的边数不大于k的一条最短路径，这条路径的长度恰为d（i）．

证明 参见文献［2］的定理1.

定理2 修正的先进先出算法和修正的固定序算法最坏情形下的计算复杂度为O（km）．

证明 在每次迭代中，由于每一条边参与Step 2的计算过程最多一次，因而每一次迭代的计算复杂度为O（m）．根据引理1，对于求解边数≤k的最短路问题，迭代次数不会超过k．因而，两个算法最坏情形下的计算复杂度为O（km）．

需要指出的是，文中提到的3个阶段的Bellman⁃Ford算法最坏情形下的计算复杂性均为O（nm）．

3 算法的实验评估

由于修正的先进先出算法、修正的固定序算法两种算法具有相同的、最坏情形的计算复杂度，因而只能通过实验来比较两个算法的计算效率．本文将进行两个实验：1）设定最短路径中的边数上限k为n／4，对两种算法在多种稀疏程度、多个规模水平下进行评估，以测试稀疏程度和计算规模两个因素对两个算法的影响，这里n为有向图的点数；2）给定计算规模，针对不同的k对两种算法进行评估，以测试不同k对算法的影响．实验所用有向图的权重服从均匀分布，可取1～100 000之间的任一整数.每种图实验10 000个例子.实验用的计算机为联想ThinkPad笔记本，CPU为Intel i5-2410M 2.30 GHz，内存为2.0 G.算法的比较都使用相同的例子.算法程序均采用结构化语言Delphi7.0.

3.1 稀疏程度和计算规模的影响实验

本文用边数与点数之比来表示图的稀疏程度.在每种图中，设计了10、50、200和1 000等4种稀疏情形进行评估，主要原因是它们代表了4种典型的稀疏程度，即：1）当稀疏程度≤10时，一般认为是超稀疏的；2）当稀疏程度≤log n时，一般认为是稀疏的，按照本文的实验规模，50接近于这个水平；3）当稀疏程度接近于n 时，一般认为是超稠密的，按照本文的实验规模，1 000接近于超稠密水平，而200可认为是稠密的水平．之所以不选择更大的稀疏程度进行实验，根本原因是：如果稠密程度＞2 000时，无法在＞100 000个点的规模水平下开展实验，将发生内存溢出，不能形成完整的实验结果以进行对比分析．

本文同时选择了12类规模水平进行试验评估，其中小规模水平（点数＜10 000的图）4种、中规模水平（点数介于10 000～100 000的图）4种、大规模水平（点数＞100 000的图）4种．k取值为n／4．之所以设定最短路径中的边数上限k为n／4，主要是保证尽可能多的迭代次数．相关评估结果如表1～12所示．

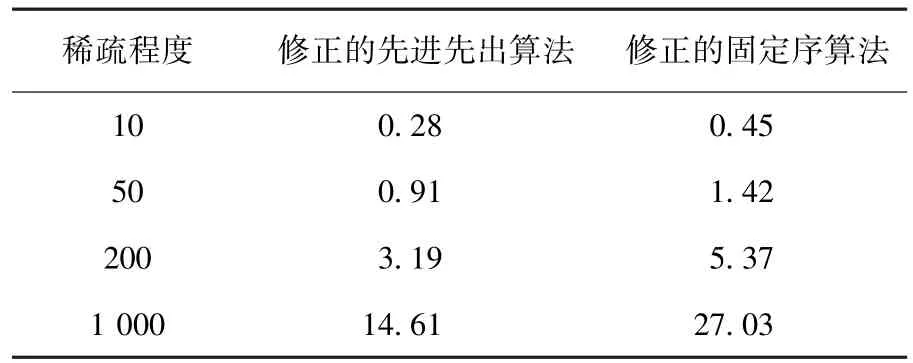
表1 2 000个点下的平均计算时间ms

表2 4 000个点下的平均计算时间ms

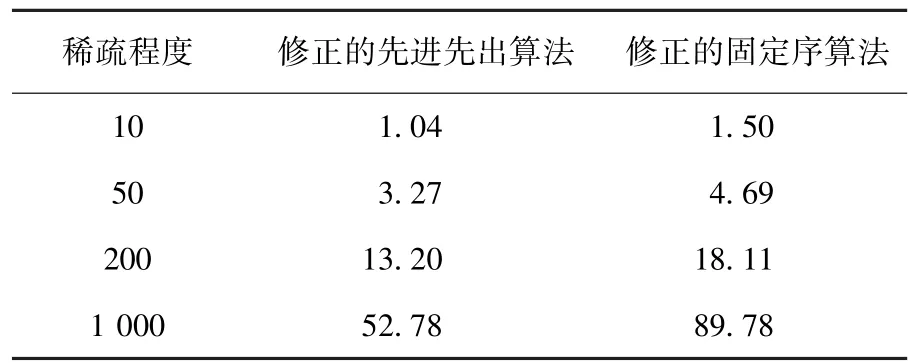
表3 6 000个点下的平均计算时间ms

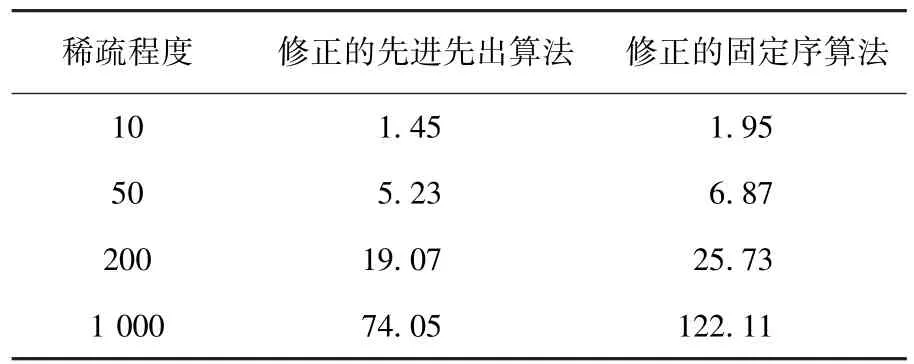
表4 8 000个点下的平均计算时间ms

表5 20 000个点下的平均计算时间ms

表6 40 000个点下的平均计算时间ms

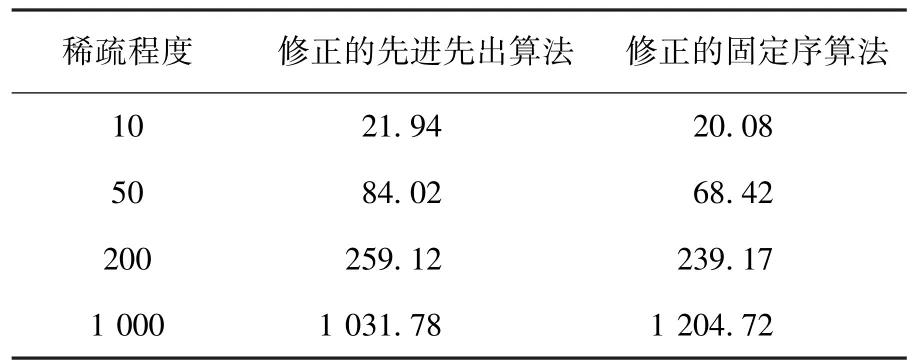
表7 60 000个点下的平均计算时间ms

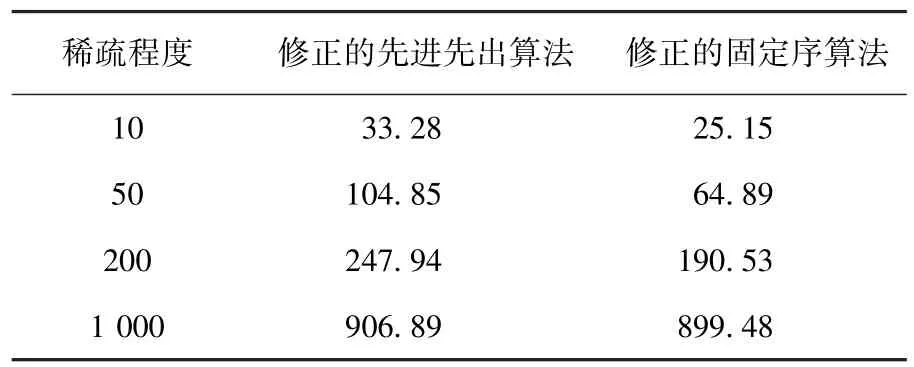
表8 80 000个点下的平均计算时间ms

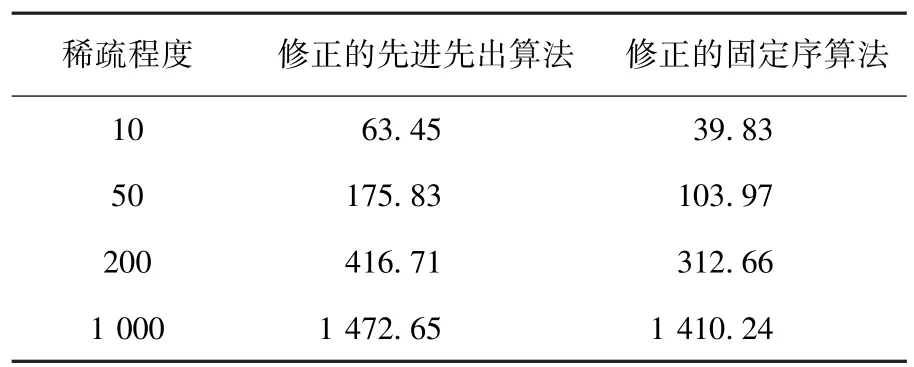
表9 120 000个点下的平均计算时间ms

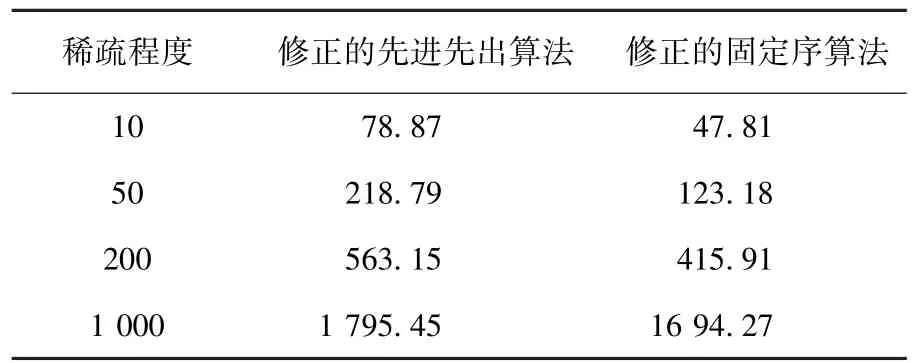
表10 140 000个点下的平均计算时间ms

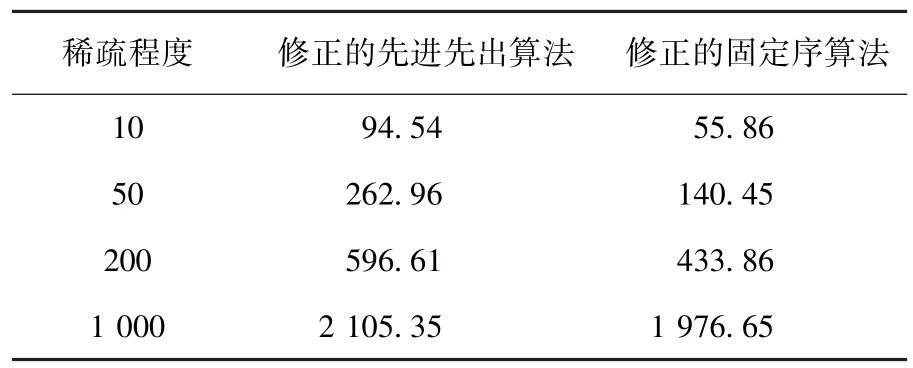
表11 160 000个点下的平均计算时间ms

表12 180 000个点下的平均计算时间ms

根据表1～12的实验数据，可得如下结论：

1）相对于修正的先进先出算法，在既定的规模水平下，随着稀疏程度的增加，修正的固定序算法的竞争优势将越来越不显著甚至丧失.如在6 000个点的规模水平下，修正的固定序算法在稀疏程度为10时具有更快的计算效率，但当稀疏程度增加为1 000时却丧失了竞争优势.

2）相对于修正的先进先出算法，在既定的稀疏程度下，随着规模水平的增大，修正的固定序算法的竞争优势将越来越显著.如在稀疏程度为10的情形下，当规模水平为2 000个点时，修正的固定序算法比修正的先进先出算法计算效率平均慢60.7%，而当规模水平为180 000个点时，修正的固定序算法反而比修正的先进先出算法计算效率平均快75.6%.

3）相对于修正的先进先出算法，当规模水平足够大时，在所有的稀疏程度下，修正的固定序算法将具备完全的竞争优势.如当规模水平＜10 000个点时，修正的固定序算法在4种稀疏程度情形下均处于劣势，而当规模水平＞80 000个点时，这个算法在所有情形下均赢得了优势.

3.2 k的影响实验

首先选择20 000个点和160 000个点两个规模水平，k分别取值为5、10、15和n／4进行实验，如表13～15所示．鉴于k为5、稀疏程度为10时，计算结果出现异常，又增加了两个规模水平（即60 000个点和100 000个点）进行实验，以给出稳定的规律，如表16所示．

根据表13～16，可得如下结论：

1）由表15可以看出，修正的固定序算法在大规模情形下具有压倒性的竞争优势，16种情形下仅当k为5、稀疏程度为10时弱于修正的先进先出算法．

2）由表15还可以看出，在给定的规模水平和稀疏程度情形下，当k取适当值时对修正的固定序算法非常有利，但当k进一步变大或变小时这种有利现象将减弱或消失．如在规模水平为160 000个点、稀疏程度为10的情形下，k为10时最为有利．

3）由表16可以看出，当k和稀疏程度同时较小时，修正的先进先出算法具有绝对的竞争优势，并随着规模的增大优势愈加突出.需要指出的是，在表16中出现了一个反常值，即计算时间值0.78，但从两个算法的计算时间比来看，规律是十分明显的.

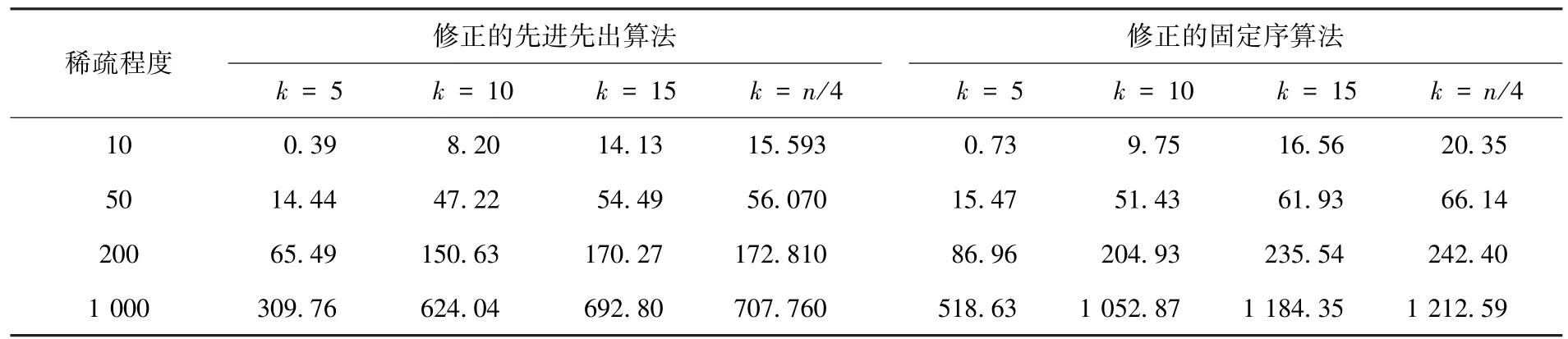
表13 20 000个点、不同k下的平均计算时间ms

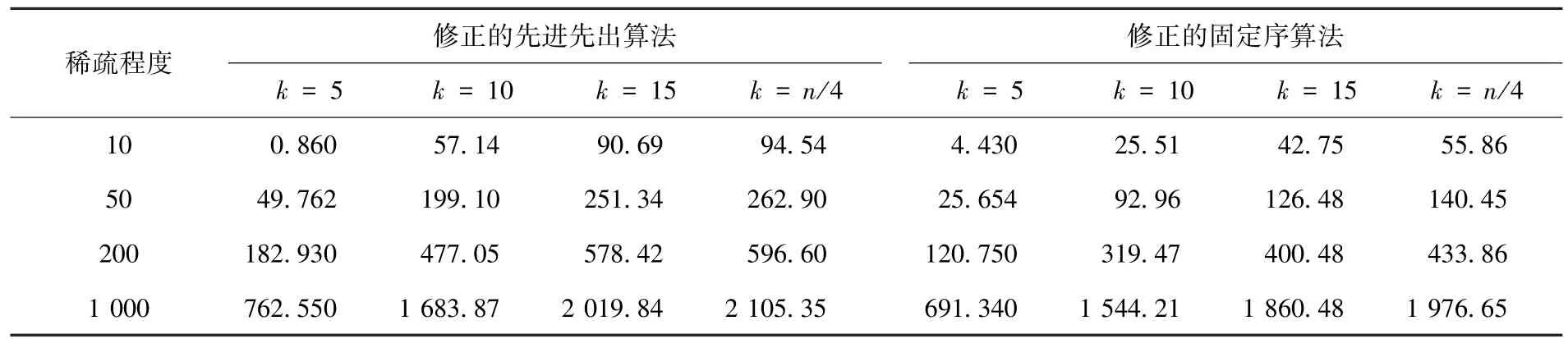
表14 160 000个点、不同k下的平均计算时间ms

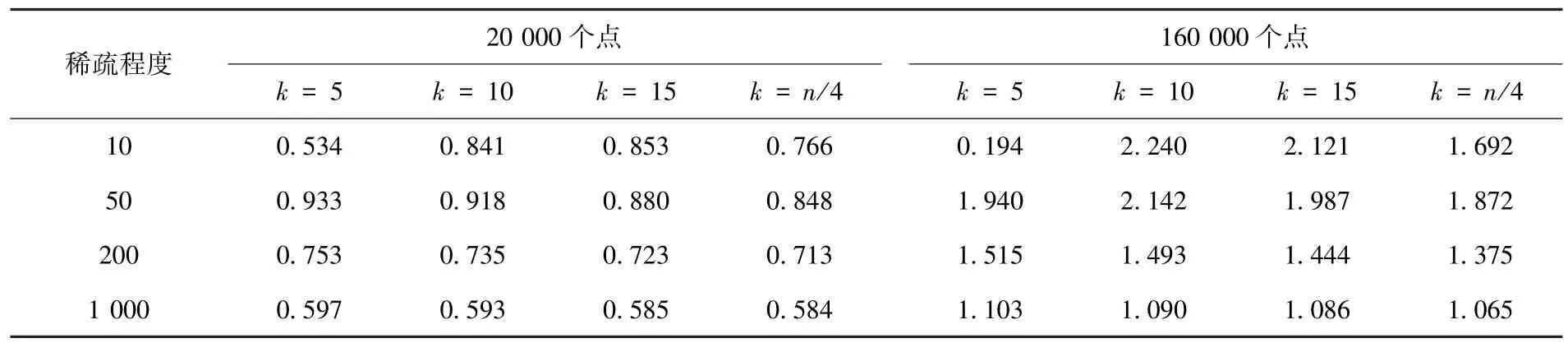
表15 修正的先进先出算法与修正的固定序算法计算时间之比

表16 k为5、稀疏程度为10、不同规模水平下的平均计算时间ms

由上述两个实验可以看出，尽管两个算法具有同样的计算复杂性，但是在不同参数、稀疏程度和规模水平下却体现了不同的计算效率.因为两个算法在Step 2中分别采取了不同的数据结构，其中修正的先进先出算法采用了优先队列来存储参与迭代的点，而修正的固定序算法则是逐一判断各点是否可参与迭代.后者相对简单，易于实现，又能在大规模情形下体现出明显的竞争优势，因而具有一定的理论和实践价值.

4 结 论

1）本文通过对固定序Bellman⁃Ford算法进行修正，获得了一种求解边数≤k的最短路问题的新算法——修正的固定序算法.

2）在大规模情形下，相对于文献［2］提出的修正的先进先出算法，修正的固定序算法相对简单、易于实现，实验表明它具有显著的竞争优势，仅仅在少数情形下处于落后状态.

［1］韩伟一，王铮.负权最短路问题的新算法［J］.运筹学学报，2007，11（1）：111-120.

［2］韩伟一.经典Bellman-Ford算法的改进及其实验评估［J］.哈尔滨工业大学学报，2012，44（7）：74-77.

［3］BELLMAN R E.On a routing problem［J］.Quarterly of Applied Mathematics，1958，16（1）：87-90.

［4］CHERKASSKY B V，GEORGIADIS L，GOLDBERG A V，etal.Shortest⁃pathfeasibilityalgorithm：an experimentalevaluation［J］.ACMJournalof Experimental Algorithmics，2009，14（2）：1-37.

［5］HUNG M S，DIVOKY J J.A computational study of efficient shortest path algorithms［J］.Computer＆Operations Research，1988，15（6）：567-576.

［6］LEWANDDOWSKI S.Shortest paths and negative cycle detection in graphs with negative weights［R］.Stuttgart：Technical Report，Stuttgart University，2010.

［7］CHERKASSKY B V，GOLDBERG A V.Negative⁃cycle detection algorithm［J］.Mathematical Programming，1999，85（2）：277-311.

［8］CHERKASSKY B V，GOLDBERG A V.Shortest paths algorithms：theory and experimental evaluation［J］. Mathematical Programming，1996，73（2）：129-174.

［9］YEN J Y.An algorithm for finding shortest routes from all source nodes to a given destination in general networks［J］.Quarterly of Applied Mathematics，1970，27：526-530.

［10］段凡丁.关于最短路径的SPFA快速算法［J］.西南交通大学学报，1994，29（2）：202-212.

［11］GOLDBERG A V，RADZIK T.A heuristic improvement of the Bellman-Ford algorithm［J］.Applied Mathematics Letters，1993，6（3）：3-6.

［12］TARJAN R E.Shortest paths［R］.Murray Hill，NJ：AT＆T Bell Laboratories，1981.

［13］GLOVER F，KLINGMAN D D，PHILLIPS N V.A new polynomially boundedshortestpathalgorithm［J］. Operations Research，1985，33（1）：65-73.

［14］GLOVER F，KLINGMAN D D，PHILLIPS N V，et al. Newpolynomialshortestpathalgorithmsandits computational attributes［J］.ManagementScience，1985，31（9）：1106-1128.

（编辑 张 红）

An improvement on fixed order Bellman⁃Ford algorithm

HAN Weiyi

（School of Economic and Management，Harbin Institute of Technology，150001 Harbin，China）

In the paper，Bellman⁃Ford algorithm with fixed order is modified in order to solve the shortest path problem with not more than k edges.After the k⁃th iteration，each path must own no more than k edges by modifying the labeling process of the origin algorithm.The modified algorithm proves true and its worst⁃case complexity is O（km）．In contrast to the modified Bellman⁃Ford algorithm with FIFO order，experiments show that the algorithm has the significant competitive advantage in the large⁃scale case.

algorithm；Bellman⁃Ford algorithm；FIFO order；fixed order；the shortest path problem

TP301.6

：A

：0367-6234（2014）11-0058-06

2004-03-02.

国家自然科学基金（71101037）；中央高校基本科研业务费专项资金（HIT.HSS.201406）.

韩伟一（1974—），男，讲师，硕士生导师.

韩伟一，wyhan＠hit.edu.cn.