细长体出水过程中阻尼系数变化分析

陈海龙，倪宝玉，孙士丽，孙龙泉

（哈尔滨工程大学船舶工程学院，150001哈尔滨）

细长体出水过程中阻尼系数变化分析

陈海龙，倪宝玉，孙士丽，孙龙泉

（哈尔滨工程大学船舶工程学院，150001哈尔滨）

针对细长体出水过程中黏性阻尼系数和兴波阻尼系数的变化，采用弹性体振动理论和流体势流理论相结合的方式对其进行研究.对于黏性阻尼项，建立简化的涡激振动模型，将涡激振动的阻力和升力项考虑到结构振动方程中，获得考虑涡激振动后的阻尼系数增量.对于兴波阻尼项，采用时域格林函数法，首先计算规则球体振动问题，并将计算结果与相关文献对比，发现二者吻合良好.在验证算法的基础上，采用细长体模型，分别计算不同振动频率和不同出水高度对于兴波阻尼系数的影响.计算结果表明：涡激振动引起的黏性阻尼增量随着洋流增大、波浪增高或者空泡长度减短而增加；兴波阻尼和细长体的出水高度、固有振型和振动频率密切相关，所对应的细长体在头部出水、振动频率0.5 Hz左右诱发的兴波阻尼最大.一阶和二阶弹性振动诱发的兴波阻尼系数较小，工程中可忽略.

细长体；振动；粘性阻尼；兴波阻尼

细长型物体在水中运行和出水过程中，会在波浪、漩涡脱落等周期性外载荷下做有阻尼强迫振动.振动过程中对应的阻尼力可能包含材料和结构内阻尼［1］，流体黏性阻尼［2］，附加质量变化引起的阻尼［3］以及兴波阻尼［4］等.材料和结构内阻尼属于材料和结构的自身属性，对于一定结构而言，其材料和结构内阻尼是固定的.对于附加质量变化引起的阻尼，与初始水深、运动速度和物体自身振动形式有很大关系，倪宝玉等［3］曾就细长体落水为例，详细推导并讨论了附加质量变化率对结构振动方程的影响，发现附加质量不仅会影响质量阵，变化的附加质量还会影响结构阻尼阵，并给出了对应主阻尼系数的增量.鉴于此，本文主要讨论细长体出水过程中流体黏性阻尼和兴波阻尼两部分的变化情况.

陶昉敏等［5］采用结构振动方程求解了物体出水过程中振动响应分析，其中考虑了附加质量和弹体结构阻尼.袁振伟等［6］考虑了横向振动圆柱体在流体中的动力学特性，总结得到流体对于圆柱体的力主要表现为动力附加质量和动力附加阻尼，即流体黏性阻尼，并进一步分析了流体黏度等因素的影响.郑帮涛［7］总结了潜射导弹出水过程中水弹道和流体动力的研究进展，包括艇速和波浪等因素的影响.应用频域和时域格林函数计算船舶运动的附加质量和兴波阻尼的算法在不断进展，但是计算水下高频振动细长体的兴波阻尼还是存在一定难度，尤其考虑到波浪、洋流和空泡溃灭载荷等多种环境因素的影响.精确而快速的求解时域Green函数及其空间导数是求解问题的关键.黄德波［8］用造表插值方法成功的解决了时域Green函数兴波部分的数值计算问题.但用该方法解决斜壁出水问题会产生不收敛现象，这是因为自由面附近的时域兴波Green函数没有考虑到自由面的张力和黏性，不符合实际情况，结果是发散的.文献［9-10］将张力和黏性引入到时域Green函数，从而消除了兴波格林函数的奇异现象.

目前关于细长体出水阻尼系数的研究中，对于黏性阻尼的考虑中很少考虑涡激振动的影响；涉及兴波阻尼系数的相关文献研究较少.为此，本文首先分析涡激振动对于黏性阻尼系数的影响；其次分析兴波阻尼的求法并与相关文献进行对比；最后进行多种算例分析各类因素如空泡、洋流、波浪或振动频率和出水高度的影响.

1 涡激振动诱发的黏性阻尼系数变化

如图1所示，定义一个随体笛卡尔坐标系O-χyz，原点O位于物体质心位置，z轴竖直向上．细长体总长为L，直径为D，附带有长度为c的肩空泡．物体顶点距离静水面高度H也称为出水高度，在本文中有H≥0．假设速度大小为u的均匀洋流来流方向沿y轴正向，入射波运动方向也沿y轴正向，与洋流同向．简化圆柱体振动模型的横剖面如图2所示，柱体在χ和y方向振动的速度分别为.χ和.y，在随体坐标系中观察来流速度，则合成的来流速度ur满足

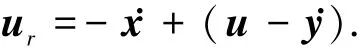
对应的攻角满足α＝arctan［-.χ／（u-.y）］．对于典型细长体，当流体绕过其截面积时，将产生漩涡脱落并发生所谓的“涡激振动”．结构单位长度上沿流向的阻力FD和垂直流向的升力FL可表达为

式中CD、CL分别为对应的阻力系数和升力系数．将二者转化随体坐标系O-χyz中，则有

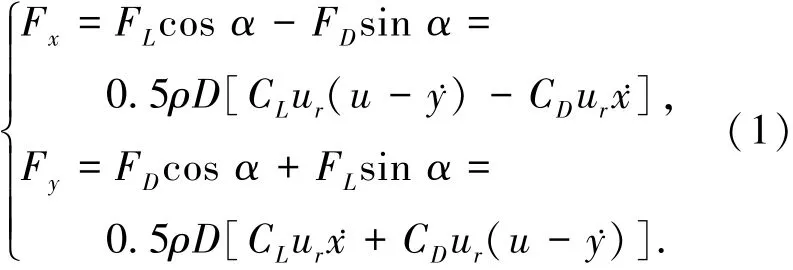
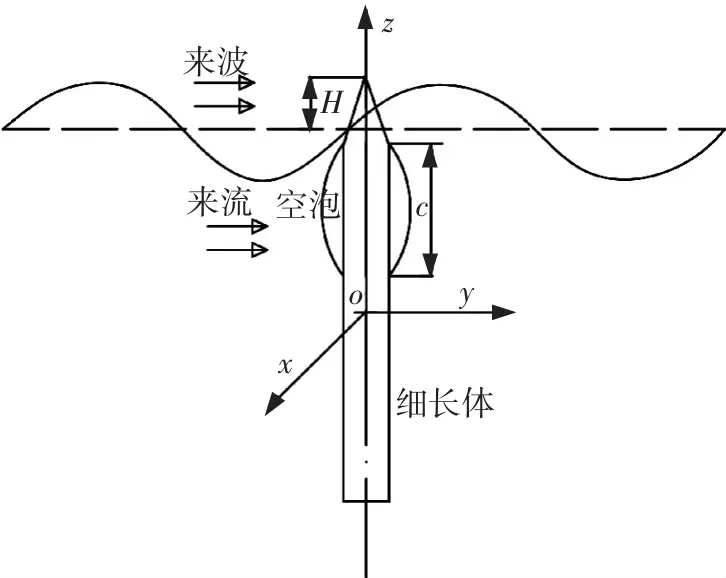
图1 细长体出水运动示意

图2 简化圆柱振动模型的横剖面

将流体力Fχ和Fy作用在细长体结构弹性振动方程中，有

式中：EI为细长体的弯曲刚度；ms为细长体单位长度分布质量；Cs为黏性外阻尼系数，这里没有考虑结构内阻尼的影响．将式（1）代入到式（2）中，并整理有

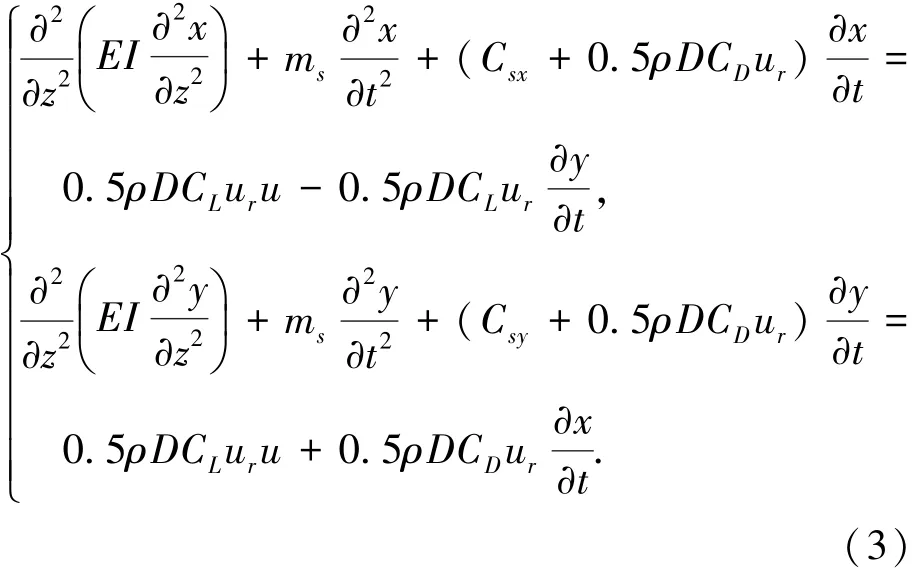
现以细长体沿流向y方向的振动为例，在主坐标系中求解细长体弹性振动方程.设y＝为细长体第j阶干模态振型，为其对应的y向分量；qj为细长体广义坐标矢量．代入式（3），方程两边同时乘以沿长度方向进行积分，考虑到正交条件，整理有

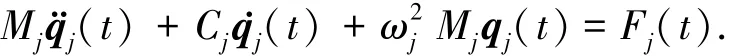
式中：ωj为细长体第j阶谐调无阻尼振动的固有频率；dl，其中ˉL＝L-c-H为有效湿表面积对应的长度，这里仅考虑空泡的存在对于物体湿表面积的影响，简单地认为空泡覆盖区物体表面积为干表面积，忽略了空泡自身运动如膨胀、脱落等引起的黏性阻尼变化．这里引入阻尼系数为

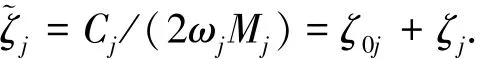
2 兴波阻尼系数变化

振动的物体在逼近自由液面以及穿越水面过程中，均会因兴起波浪而产生兴波阻尼.兴波阻尼系数与物体的振动频率和出水高度等均有关系.这里假设结构在规则波作用下做微幅简谐运动（振动），基于流体的势流理论［4］和结构的干模态法［2］推导兴波阻尼系数.仍将细长体结构视为连续弹性体，细长体位移和含义同上．第j阶模态的广义力为［2］

式中：SI为有效湿表面积；为第j阶模态的法向分量；p（χ，y，z，t）为流固耦合交界面处的流体压力．在微幅运动（振动）的假设下，忽略二阶项，仅保留伯努利方程中［4］中线性项为

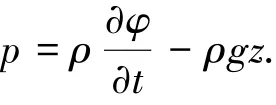
式中：ρ为流体密度；g为重力加速度；t为时间；φ为速度势．

当结构在规则波作用下做微幅简谐运动（振动），按线性叠加原理，满足Laplace方程和边界条件的速度势φ可分解如下［4］

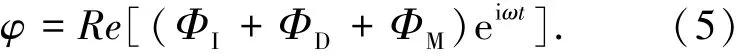
式中：ΦI为入射速度势，即当结构物不存在时的入射波引起的速度势；ΦD为绕射速度势，此为假定结构物为刚体且固定不动时波浪所引起的速度势；ΦM为辐射速度势，由于结构物运动或振动引起的速度势，ω为圆频率．设主坐标稳态解qj为

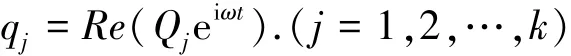
式中Qj为复数，则结构z向位移满足

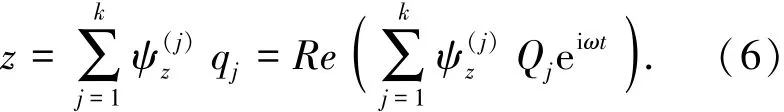
式中ψ（j）z为第j阶模态的z向分量．设辐射速度势φM为

式中φj为对应于第j阶干模态的速度势，满足边界条件

将式（5）～（7）带入式（4）中整理有

或

Lj为广义波浪激励矢量L的元，即L＝；Mjs，Bjs和Sjs分别为附加质量阵Mf，兴波阻尼阵Bf和附加刚度阵Sf的元，即Mf＝［Mjs］，Bf＝［Bjs］，Sf＝［Sjs］．由于Bjs和物体运动或振动的速度成正比，故被称为兴波阻尼系数．关于格林函数的具体计算方法详见文献［4，11］．

3 算例分析

3.1 数值有效性验证

基于势流理论，本文采用时域格林函数，开发三维计算程序，计算细长体前两阶湿模态下兴波阻尼系数的变化规律.在探讨规律之前，先通过简单的圆球体运动验证本文程序的有效性.如图3所示，选取半径为1 m的圆球，令其初始球心位于自由面上，分别令其做微幅垂荡（z方向，也定为3方向）和纵荡（y方向，也定为2方向）运动，计算不同频率（波数）条件下对应的兴波阻尼系数，并与文献［12］中Hulme的计算结果对比，如表1所示，对于无限水深，波数KR＝ω2／g＝（2πf）2／g，ω和f分别为振动的圆频率和频率．

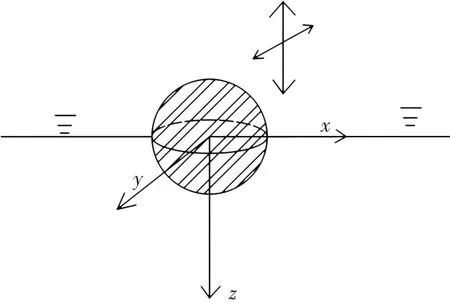
图3 圆球自由面振动模型

表1 兴波阻尼系数对比表

表1中B33＿H和B22＿H分别表示文献［12］中Hulme计算的垂荡和纵荡的阻尼系数，B33和B22分别表示本文时域格林函数得到的阻尼系数，误差＝｜Bii-Bii＿H｜／Bii＿H×100%（i＝2，3）．从表1中对比可以看出，时域法求解垂荡兴波阻尼B33的最大误差为8.68%，最小误差为0.45%；时域法求解纵荡兴波阻尼B22的最大误差为7.89%，最小误差为0.18%．可见最大误差均不超过10%，说明本文数值有较高的精度，验证了本文数值模型计算振动物体兴波阻尼的正确性和有效性．此外，容易发现兴波阻尼并非随振动频率单调变化的，而是先增大后减小．

3.2 不同环境条件下黏性阻尼系数变化

图4为静水中，在不同空泡长度条件下，细长体在一阶和二阶固有频率下振动时阻尼系数的变化情况.可见随着空泡长度增加，物体湿表面面积减小，阻尼系数减小.一阶和二阶的弹性振动阻尼系数均在0.06左右，变化范围较小.对比一阶和二阶固有频率下阻尼系数的变化，发现二阶固有频率下阻尼系数变化的幅度更小，说明二阶固有频率下阻尼系数对于湿表面积的变化更不敏感.

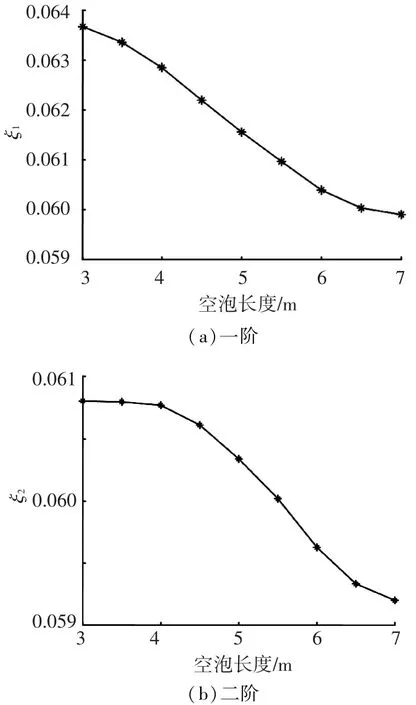
图4 静水中黏性阻尼系数随空泡长度变化情况

图5 为有均匀来流、无波浪条件下，细长体在一阶和二阶固有频率下振动时阻尼系数的变化情况.选取均匀来流变化范围u＝0～3 m／s，图5中阴影对应的上下限分别为空泡长度c为3 m和7 m的工况.可见随着来流速度增加，一阶和二阶固有频率下阻尼系数均基本呈线性增大趋势，但曲线斜率较小，即其随来流速度变化缓慢.

图6为无来流、有规则波浪条件下，细长体在一阶和二阶固有频率下振动时阻尼系数的变化情况.选取艾里波模型，令波高变化范围0～6 m，图6中数据点的上下限同上，阴影区域的曲线是通过数据点最小二乘法拟合得到的.可见随着波高增加，细长体阻尼系数将呈现非线性增大趋势，且相对于空泡和洋流的影响，波浪对于阻尼系数的影响更加明显.

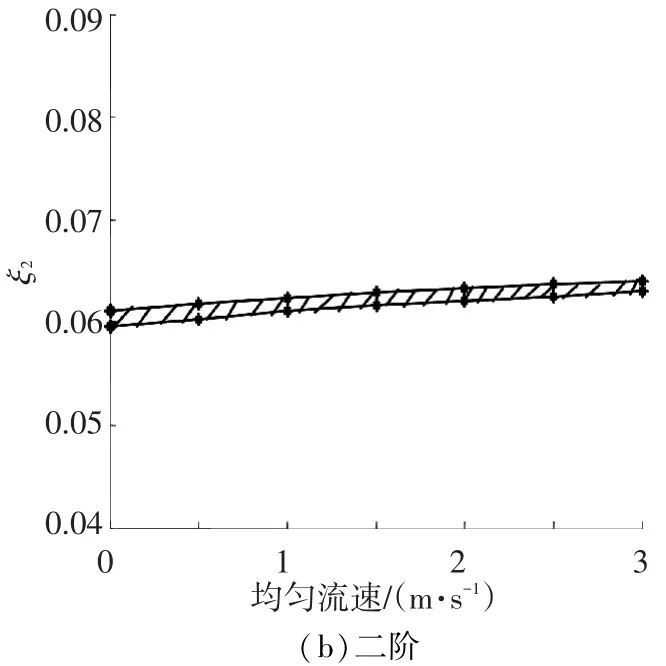
图5 均匀流下黏性阻尼系数变化情况

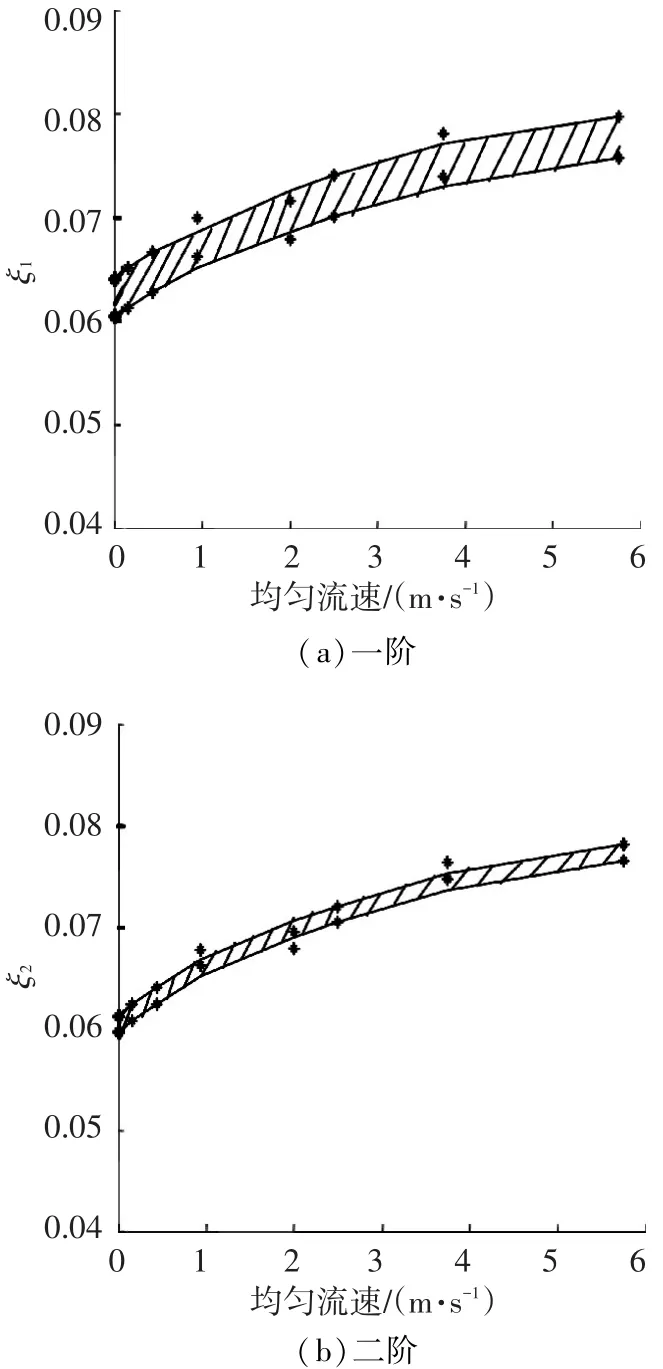
图6 规则波下阻尼系数变化情况

3.3 不同频率和出水高度下兴波阻尼系数变化

为了考虑振动频率f对于兴波阻尼系数的影响，本文取出水高度H＝1 m，细长体沿y方向以不同频率f做微幅振动，环境条件取为无流、无浪和无空泡的静水．图7为兴波阻尼系数随振动频率的变化曲线，从图7中可见，兴波阻尼对于频率的变化十分敏感：当f＜0.5 Hz时，兴波阻尼系数随频率增加而增大；当f＞0.5 Hz后，兴波阻尼迅速减小；当f＞1.5 Hz后，兴波阻尼系数逐渐趋近于0．0.5 Hz对应的最大阻尼系数接近0.2．可见，频率只有在很小的情况下会对兴波阻尼造成影响；频率较大后，可以近似忽略兴波阻尼效应．

图7 兴波阻尼系数随振动频率变化曲线

为了考虑出水高度H对于兴波阻尼系数的影响，本文取细长体一阶和二阶弹性振动固有频率，改变出水高度H＝0～14 m.环境条件取为无流、无浪和无空泡的静水.图8（a）、（b）分别为不同出水高度下细长体在一阶和二阶固有频率下振动引起的兴波阻尼系数.从图8中可见细长体未露出水面时，弹性振动引起的兴波阻尼很小，基本接近于0，所以细长体未露出水面之前，弹性振动引起的兴波阻尼可以忽略不计.当H＝1 m时，弹性振动引起的兴波阻尼达到峰值，当H继续增大，物体继续出水时，兴波阻尼系数反而迅速下降，在很小的幅值范围内波动.兴波阻尼系数的峰值位置和波动趋势与细长体的固有振型有关，一阶和二阶弹性振动诱发的兴波阻尼系数有类似的趋势，只是二阶兴波阻尼系数较之一阶小得多.从图8中可见，一阶和二阶固有频率下兴波阻尼系数的量值均很小，工程计算中可忽略因细长体弹性振动而引起的兴波阻尼.

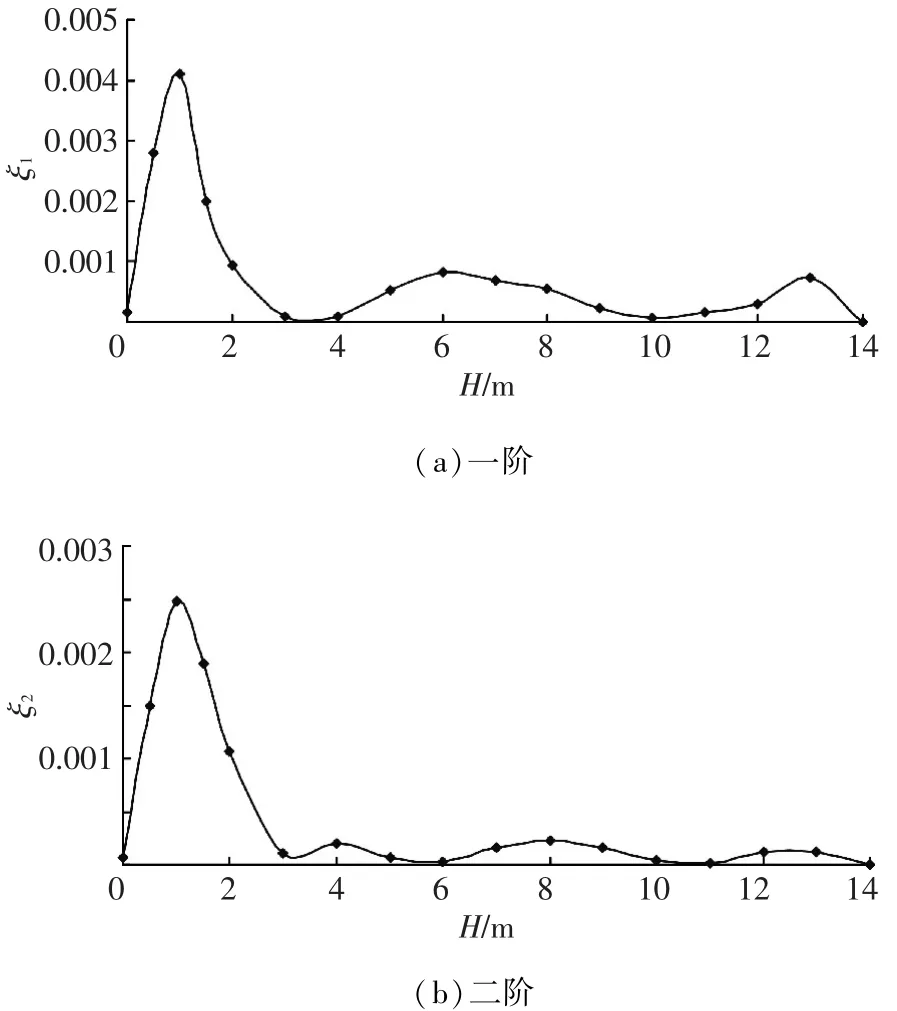
图8 不同出水高度下弹性振动兴波阻尼系数

4 结 论

1）涡激振动引起的黏性阻尼增量与细长体出水的海洋环境关系密切，洋流越大、波浪越大或者空泡长度越短，均导致涡激振动引起的黏性阻尼增量增加.

2）兴波阻尼对细长体的振动频率十分敏感，仅在振动频率很低时（1.5 Hz以内）兴波阻尼有较大影响，振动频率趋近0或者大于1.5 Hz后，兴波阻尼几乎为0.

3）兴波阻尼和细长体出水高度和固有振型有关，在本文研究的细长体模型中，头部出水时刻诱发的兴波阻尼最大；一阶和二阶弹性振动诱发的兴波阻尼系数量值均较小，在工程中可忽略该项阻尼系数.

［1］姚熊亮.船体振动［M］.哈尔滨：哈尔滨工程大学出版社，2004.

［2］姚熊亮.舰船结构振动冲击与噪声［M］.北京：国防工业出版社，2007.

［3］倪宝玉，孙士丽，孙龙泉，等.弹体落水过程中附加质量变化影响研究［J］.振动与冲击，2012，31（14）：171-176.

［4］戴遗山，段文洋.船舶在波浪中运动的势流理论［M］.北京：国防工业出版社，2008.

［5］陶昉敏，孙雁，刘正兴.潜射导弹出水过程响应分析［J］.上海力学，1998，19（2）：99-108.

［6］袁振伟，褚福磊，王三保.横向振动圆柱体在流体中的动力学特性［J］.工程力学，2006，23（8）：49-52.

［7］郑帮涛.潜射导弹出水过程水弹道和流体动力研究进展［J］.导弹与航天运载技术，2010（5）：8-11.

［8］黄德波.时域Green函数及其导数的数值计算［J］.中国造船，1992（4）：16-25.

［9］CHEN X B，DUAN W Y.Capillary⁃gravity waves due to an impulsive disturbance［C］／／Proceedings of 18th International Workshop on Water Waves and Floating Bodies.Carry⁃Le⁃Rouet.France：［s.n.］，2003：29-32.

［10］CHEN X B，DUAN Wenyang，LU Dongqiang.Gravity waves with effect of surface tension and fluid viscosity［J］.Journal of Hydrodynamics，Ser B，2006，18（3）：171-176.

［11］张阿漫，姚熊亮.近自由面水下爆炸气泡的运动规律研究［J］.物理学报，2008，57（1）：339-353.

［12］HULME A.The wave acting on a floating hemisphere undergoing forced periodic oscillations［J］.Journal of Fluid Mechanics，1982，121：443-463.

（编辑 张 红）

Variation of the damp coefficients of a slender body during water exit

CHEN Hailong，NI Baoyu，SUN Shili，SUN Longquan
（College of Shipbuilding Engineering，Harbin Engineering University，150001 Harbin，China）

To study the variation of the damp coefficients of a slender body during water exit，the vibration theory of an elastic body and the potential flow theory of fluid are adopted.For viscous damp coefficient，vortex induced vibration（VIV）model is introduced and the lift and drag forces are included in the structure vibration equation.The increment of damp coefficient by VIV is therefore obtained.For wave⁃making damp coefficient，time⁃domain Green Function is adopted.The problem of a sphere oscillating on the free surface is calculated first and compared with the published paper，and the results agree well with each other，which validates the numerical model and procedure in this paper.Based on this，the wave⁃making damp coefficient of a slender body under different vibration frequencies and different lengths during water exit are calculated and analyzed.The results show that the increment of damp coefficient by VIV rises with the increase of current，wave and the reduction of cavitation，while the wave⁃making damp coefficient is closely related to the length of water exit，the natural vibration mode and the vibration frequency of the slender body.For the case studied in this paper，the wave⁃making damp coefficient peaks when the head of the body comes out of the water and the vibration frequency is around 0.5 Hz，and the wave⁃making damp coefficient induced by the first and second order elastic vibration respectively is quite small，which can be neglected in the engineering application.

slender body；vibration；viscous damping；wave⁃making damping

U664.113

：A

：0367-6234（2014）11-0084-06

2014-02-24.

中国博士后科学基金（2013M540272）；高等学校博士学科点专项基金（20132304120027，20132304120028）；中央高校基本科研业务费专向资金（HEUCF140116）；海洋工程国家重点实验室（上海交通大学）开放课题（1309），黑龙江省博士后基金（LBH-Z13051）.

陈海龙（1980—），男，博士，副教授.

倪宝玉，nibaoyu＠hrbeu.edu.cn.