亲电取代反应中活性位点预测方法的比较

付 蓉 卢 天 陈飞武

(北京科技大学化学与生物工程学院化学与化学工程系,北京100083)

1 引言

亲电取代反应是有机化学反应中最基本的反应类型之一.芳香族化合物的亲电取代反应是其典型的代表.常见的包括硝化、卤化、磺化等反应.不同类型和不同条件下亲电反应的具体机理存在一定差异并且存在争议.由于量子化学研究手段的不断更新,常常有新的观点被提出来.1-4目前被广为接受的亲电反应的基本过程可以描绘成图1.5显正电性的亲电试剂会首先进攻电子丰富的芳环,形成π络合物.在经历较高势垒后,它与芳环上的一个碳原子成键而构成σ络合物.这也被称为Wheland中间体,它是一种碳正离子中间体.最后,质子从这个碳上脱去,从而结束整个反应过程.由于不同位点形成σ络合物的难易程度存在差异,芳香亲电取代反应具有明显的区域选择性.这是由芳香化合物的电子结构特点所决定的.对于取代苯体系而言,取代基的特征会显著影响苯环的电子结构,因此不同取代基会产生不同的定位效应.除了化合物自身的电子结构特点外,亲电试剂类型、位阻效应、溶剂、反应温度等诸多因素也会影响各个位点发生亲电取代的难易程度,但这些效应往往相对次要.

通过理论方法预测芳环上发生亲电反应的位点,不仅是理论化学上的一个重要课题,对于实际应用也具有重大意义.若能可靠地预测出不同位点反应活性的高低,由此论证反应的可行性,评估副产物产率,对有机合成路线的设计将起到重要的指导作用,在化工生产上也能防止不必要的浪费而获得经济效益.理论上预测反应位点最为准确可靠的方法是做从头算动力学模拟,6它可以将各种影响反应过程的效应全面地考虑.然而从头算动力学计算过于耗时,很难用于实际问题的讨论.另一种分析方法是基于过渡态理论进行计算,1-3通过反应势垒考察在不同位点上反应的难易,但这种研究方式较为复杂繁琐.还有一大类方法完全基于反应物自身性质来对反应位点进行预测,可以直接指出不同位点发生反应的难易,在计算和分析上都非常快捷方便,这正是本文所要讨论的方法.这类方法数目众多,原理各有不同,包括前线轨道理论、7福井函数、8双描述符、9静电势、10原子电荷、11平均局部离子化能12等.虽然这类方法得到了广泛应用,但是它们的可靠性一直以来缺乏系统的检验和对比,各自的优缺点不甚明确.因此面对新体系时,化学工作者往往难以选择出最合适的方法来对反应位点进行预测.

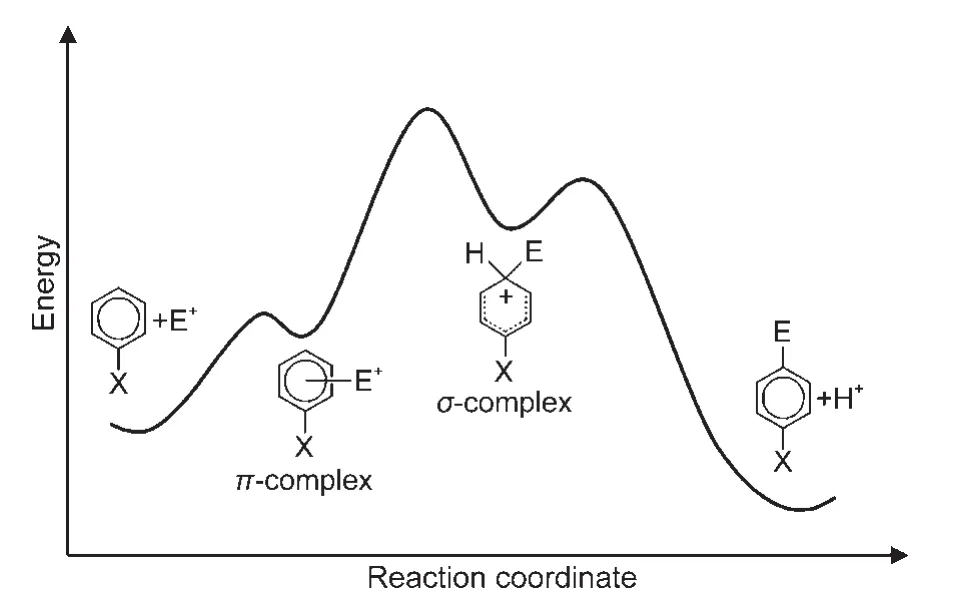
图1 芳香亲电取代过程的能量变化示意图Fig.1 Energy profile for an aromatic electrophilic substitution process

取代苯是亲电取代反应最常涉及的反应物,种类丰富,而且不同位点发生反应的产率数据易于获得,因此是十分理想的测试体系.本文选择大量的取代苯体系作为测试集,分析对比各种最常用的预测亲电位点方法的结果,并评估它们的可靠性.

2 预测反应位点的方法

2.1 静电势

静电势描述了位于某一点r的单位正电荷与当前体系的相互作用能10,13-15

其中Z是原子A的核电荷,R代表原子核坐标,ρ是电子密度.由式(1)可见,静电势由原子核电荷和电子密度两部分组成,前者贡献正值,后者贡献负值.静电势为正(为负),说明此处静电势由核(电子)的电荷所主导.在原子核附近静电势总为正值,而在离核较远处静电势可正可负,这与体系的电子结构特点直接相关.分子范德华表面上的静电势分布长期以来被用于预测亲电和亲核反应位点,14-19静电势越正(越负)的区域被认为越有可能吸引亲核(亲电)试剂进攻而发生反应.通常所选用的范德华表面是由Bader所定义,即电子密度为0.001 a.u.的等值面.20考察分子表面静电势分布的常见方法是将静电势根据数值以不同颜色投影到分子表面上,这样的图形化分析十分直观.但如果想将讨论提升到定量层次,可以利用定量分子表面分析算法.21该方法可以确定出静电势或平均局部离子化能等实空间函数在分子范德华表面上的极大点和极小点.通常认为距离分子表面上静电势最小点(最大点)位置最近的原子将是最可能发生亲电(亲核)反应的位点.

对于苯衍生物,由于芳环上的原子基本处在同一个平面上,所以也可以计算每个碳原子在垂直于环平面方向上0.16 nm处(约为碳原子的范德华半径)的静电势,并相互比较大小.22静电势越负的碳原子越可能参与亲电反应.

2.2 平均局部离子化能

平均局部离子化能(ALIE)早在1990年就被提出,23但近年来才广泛流行.12,24它的定义为

其中ρ代表总密度,ρi代表第i个占据的分子轨道所对应的电子密度,εi代表第i个分子轨道的能量.一般意义的电离能是整个体系的性质,而Iˉ(r)则体现了局部位置上电子的电离能.Iˉ(r)具有广泛的应用价值,例如展现原子壳层结构、衡量电负性、预测pKa、表现局部极化率等,而它最重要的应用则是预测反应位点.12,24Iˉ(r)数值越低,表明此处的电子被束缚得越弱,因此活性越高,越容易参与亲电或自由基反应.利用定量分子表面分析技术,可以获得Iˉ(r)在分子表面上的极小点位置和数值.12,21若某原子处在数值越小的极小点附近,则该原子的反应活性越高.若原子附近的分子表面上没有Iˉ(r)极小点出现,则表明此原子参与反应的可能性很小.

类似于分析静电势,对于苯衍生物也可以计算每个碳原子在垂直于环平面方向上0.16 nm处的Iˉ(r),22数值越小的碳原子越可能参与亲电或自由基反应.

2.3 原子电荷

原子电荷是对化学体系中电荷分布最简单、最直观的描述方式之一.容易理解,电荷越负(越正)的原子越有可能吸引亲电(亲核)试剂进攻而发生反应.计算原子电荷的方法极多,常见的如Mulliken、25CHELPG、26NPA、27Hirshfeld、28ADCH、29AIM.30不同方法计算的原子电荷特点不同,往往有较大数值差异,在文献11中有详细的对比讨论.在本文中我们将检验其中常用的几种原子电荷预测亲电位点的能力.

2.4 前线分子轨道理论

福井谦一31提出的前线轨道理论认为,体系的最高占据轨道(HOMO)和亲电反应有关,体系的最低空轨道(LUMO)和亲核反应有关.根据HOMO或LUMO的轨道成分多少可以判断发生亲电反应或亲核反应的位点.分析HOMO(LUMO)的轨道成分等同于考察这个轨道(设为第i个轨道)的电子密度(ρi=|φi|2))在各原子附近分布的总量.有多种方法都可以计算分子轨道中原子的成分,例如Mulliken方法、AOIM方法、Hirshfeld方法.文献32对此有详细的介绍和讨论.本文分析HOMO成分使用的是基于自然原子轨道概念(NAOMO)的方法.32这种方法计算速度快,结果合理,而且基组依赖性很小,十分适合分析占据轨道的成分.NAOMO的缺点是不适合分析LUMO的成分.

2.5 福井函数

1984年Parr和Yang提出的福井函数是概念密度泛函理论框架中的一个重要概念,8,33,34已被广泛地用于预测反应位点.通常认为,福井函数越大的位点,其相应的反应活性也越大.福井函数定义为

其中N代表当前体系中的电子数,μ是体系化学势.ν(r)代表原子核对电子产生的吸引势,由体系的几何结构所决定.电子密度相对于N的偏导数在N为整数时是不连续的,因而式(3)无法直接计算.通过有限差分近似来计算它的左导数、右导数以及二者的平均值,福井函数可以分别与三种类型反应联系起来,即

式中ρN、ρN+1和ρN-1分别代表体系在原始状态(N电子)、结合一个电子状态(N+1电子)和电离掉一个电子状态(N-1电子)下的电子密度.值得注意的是,由于式(3)要求外势不变,因此,采用式(4)计算ρN-1(r)、ρN(r)和ρN+1(r)时,体系的几何结构应当都一样.

由式(4)可看出,f-展现的是当体系因受到亲电试剂进攻而电子转移走时各个位置上电子密度的变化程度,这体现出不同区域的电子参与亲电反应的能力.式(4)也显示了如果忽略掉轨道的弛豫效应,福井函数就还原到前线轨道理论.换句话说,前线轨道理论是在轨道弛豫效应不显著的情况下对福井函数的一个合理的近似.

最直观方便的考察福井函数分布的方式是观察它的等值面.被福井函数等值面涵盖程度越大的原子越可能发生相应类型的反应.所谓的简缩福井函数(CFF)35是将福井函数收缩到原子上.这样,每个原子具有一个确切数值,便于在定量层面上比较不同位点上福井函数的大小.因此,CFF可以基于原子电荷来计算

值得注意的是基于不同种类原子电荷所得到的CFF往往存在较大差异,从而影响活性位点的判断结果.哪种原子电荷最适合计算CFF并不明确,Mulliken、CHELPG、ADCH等计算原子电荷的方法都曾被用来获得CFF.35-38本文在计算CFF时基于Hirshfeld原子电荷,这种做法的合理性已经过检验.38

2.6 双描述符

2005年由Morell、Grand和Toro-Labbé提出的双描述符(DD)也是在概念密度泛函理论框架下定义的一种实空间函数.9它与福井函数有密切的关系33

其中η是体系的化学硬度.通过有限差分近似,可以得到双描述符的具体计算公式

原文指出DD为负值的区域易受亲电进攻,为正值的部分易受亲核进攻.然而在我们的实际研究中发现这个结论并非总是合理,一些易于发生亲电反应位点的DD也可能为正值,但数值通常小于不易发生亲电反应的位点.我们通过DD讨论分子内各个位点的相对活性时遵循的规则是:DD数值越负的区域越可能是亲电位点,数值越正则越容易遭受亲核进攻.

双描述符与福井函数的一个明显差异是,双描述符可以同时展现亲核与亲电反应位点而不需要分别考察f+和f-,因此更为便利.即使只讨论亲电反应,由于双描述符还引入了N+1状态下的电子结构信息,因此结论与f-也会有所不同.

类似于福井函数,双描述符的分布通常以等值面图的方式来考察,但也可以计算简缩双描述符(CDD)以便于定量比较每个位点上DD的大小

和计算CFF时一样,计算CDD时也采用Hirshfeld电荷.

2.7 pz轨道布居数

芳环上的π电子及相应的π轨道与各个位点的亲电反应活性关系最为密切.这些轨道由垂直于苯环的p型原子轨道构成.若芳环处于XY平面,则这些原子轨道就是pz轨道.pz轨道布居数越大的原子,由于其具有越丰富的π电子,越可能参与亲电反应,因此,我们提出以pz轨道布居数的大小来预测亲电反应的活性位点.这种预测方法与原子电荷最主要的区别是完全排除了σ电子的影响.由于σ电子对于亲电反应的影响远不及π电子直接,所以,将σ电子的干扰排除后将有可能提升预测能力.

由于使用扩展基的量子化学计算中,并没有明确的原子轨道的概念,32所以需要先还原出原子轨道才能得到其布居数.本文中,我们采用自然布居分析方法(NPA)27来计算价层pz自然原子轨道的布居数,而缺乏化学意义且占据数极低的里德堡型pz轨道则完全被忽略.

Pearson的硬软酸碱理论(HSAB)认为,较硬的路易斯酸容易与较硬的路易斯碱相互作用,较软的路易斯酸容易与较软的路易斯碱相互作用.39硬-硬相互作用中静电作用作为主导,反应物的电子结构变化较小.而对于软-软作用,则是轨道相互作用为主导,会产生电子云的明显极化或电荷转移.在亲电反应过程中,电子丰富的底物和缺乏电子的亲电试剂分别对应于路易斯碱和路易斯酸.基于HSAB的观点,我们可以将前述一系列预测反应位点的方法从原理上分为两大类.一类方法主要是基于静电效应来进行预测,包括静电势、原子电荷、pz轨道布居数,它们着重表现的是不同位点的硬度;而其余的方法,诸如Iˉ(r)和福井函数,它们都体现了不同区域因电子密度发生变化而参与反应的能力,故都可以认为是对局部软度的描述.注意Yang和Parr40曾经将局部软度的计算方法具体地定义为福井函数与全局软度的乘积,而本文在涉及到局部软度时则指的是一种概念,而非特定的计算方式.

形成σ络合物的过程可以假定分为两个阶段.第一阶段的重点是通过静电吸引将亲电试剂拉到反应位点,第二阶段是电子发生转移并伴随着新键生成.因此,体现静电效应和体现局部软度的两大类预测方法在一定程度上是互补的,有人建议相互结合使用.24但是,当二者的预测结果相互冲突时,将难以判断各个位点发生反应的优先顺序.有鉴于此,探寻预测能力最佳的单一方法仍是很有必要的.

除本节介绍的方法之外,还有其它一些手段可以预测和解释不同位点发生亲电取代活性的大小,例如相对亲核/亲电性、41Parr函数、42电子定域化函数、43,44电子密度拉普拉斯函数、45,46亲电体亲合力、47活化硬度、48局部极化能、22局部极化率.49但由于这些方法使用较少或者不很适合本文所研究的体系,在本文中不做讨论.

3 测试集和计算方法

本文的测试体系由14个单取代苯和8个双取代苯组成.在单取代苯当中,8个带有邻对位定位基,包括 O-、OH、NH2、CHCH2、NHCOCH3、F、Cl和CH3;其余6个带有间位定位基,包括CN、CHO、NO2、SO3H、COCH3和CF3.双取代苯已在图2中列出,S1至S4所携带的两个取代基的定位效应是协同的,定位效应能够相互增强.而C1至C4所携带的两个定位基定位效应是冲突的,定位效应会在一定程度上相互抵消.测试集分子的实验产率数据从文献50-54中获得,对应于普通反应条件下的硝化反应.由于硝化反应是最具有代表性的亲电取代反应类型,所以将它的产率数据作为参考是理想的选择.

仅仅预测出体系的首要反应位点是不够的,我们还考察各种预测方法是否能将各个位点之间的反应活性大小的相对差异正确重现,因为只有达到这个要求的预测方法才有可能对实验的产物比例进行估计,并产生实际的应用价值.至于分子间反应活性的相对差异则不属于本文的讨论范畴.为了使计算结果明确直观,我们采用“>>”、“>”、“≥”和“≈”这四种符号表示各个位点之间活性的相对大小,它们分别表示“远远大于”、“大于”、“大于等于”和“约等于”.我们还根据预测结果与实验结果的差异对预测结果进行打分.打分的基本原则是:如果预测的结果与实验结果几乎完全一致,将会给10分;如果有一定差异,但是能将取代基的基本定位效应表现出来,将会给7分左右;如果预测结果与实验结果相差极大而没有任何意义,则给0分.由于实际情况较为复杂,分值是根据预测结果的合理程度进行酌情调整的.

图2 测试集中的双取代苯体系Fig.2 Disubstituted benzenes in the test set

对于单取代体系,邻位的两个碳以及间位的两个碳都是化学等价的,但由于受到基团的朝向影响,在分子的最稳定结构下它们并非完全等价,因此分析结果也并不完全一致.我们在计算时将等价的碳的计算结果取平均来解决此问题.为了使预测结果与实验结果有可比性,实验测定的邻位、间位取代的产率都已被除以2.对于双取代体系,化学等价的碳的计算结果也同样被取平均,并且以符号≡注明等价性.

预测亲电位点的方法既包含体现局部软度的方法,也包含基于静电效应的方法.体现局部软度的方法我们将检验以下7种,它们在下文中被统称为第一类方法.冒号前标注的是它们在后文中的缩写.

(1)FF:福井函数等值面;

(2)CFF:基于Hirshfeld电荷计算的简缩福井函数;

(3)DD:双描述符等值面;

(4)CDD:基于Hirshfeld电荷计算的简缩双描述符;

(5)HOMO:由NAOMO方法计算的HOMO轨道成分;

(6)ALIEmin:分子范德华表面平均局部离子化能的极小点和数值;

(7)ALIE(1.6):原子在垂直于环平面上方0.16 nm处的平均局部离子化能数值.

基于静电效应的方法,我们也考虑7种,它们在下文中被统称为第二类方法.这些方法如下:

(1)ESPmin:分子范德华表面静电势极小点的分布和数值;

(2)ESP(1.6):原子在垂直于环平面上方0.16 nm处的静电势数值;

(3)pz-pop:垂直于苯环平面的p型原子轨道的布居数;

(4-7)Hirshfeld、CHELPG、Mulliken、NPA:表示这些方法计算的原子电荷.

本文中电子波函数的获得以及几何结构的优化都是通过Gaussian 03程序完成的.55计算过程使用B3LYP杂化泛函56结合6-31+G*基组.57-59除了CHELPG电荷、NPA电荷以及pz轨道布局数(pz-pop)采用Gaussian 03程序计算外,其它的计算包括图像的绘制都是通过我们开发的Multiwfn多功能波函数分析程序完成的.此程序可以免费下载.60,61注意由于Mulliken方法对基组的敏感性极高,特别是存在弥散函数时难以得到有意义的结果,11,32在计算Mulliken电荷时使用的基组改为6-31G*,而几何结构依然是在B3LYP/6-31+G*级别下优化得到的.

4 结果与讨论

在本节中,我们依次对第3节中介绍的含有单个邻对位定位基的取代苯体系、含有单个间位定位基的取代苯体系,以及同时含有两个定位基的取代苯体系,采用第2节介绍的方法来计算相应苯环上的反应活性位点,并比较和分析每个方法的可靠性.

4.1 含有单个邻对位定位基的体系

第一类方法和第二类方法对于含有单个邻对位定位基的体系的预测结果分别列于表1和表2,以实验产率为参照所给出的打分同时列于表中.为了便于横向比较不同方法的整体预测能力以及稳健性,在最后两行也给出了每种方法的平均分和最低分.

由表1可以看出,第一类方法,即各种表现局部软度的方法都能较好地预测出各个位点亲电活性的相对大小,即邻对位活性最大,间位活性最小.在所有这些方法中,福井函数表现最为出色,对所有分子给出的各位点反应活性顺序都与实验结果几乎完全一致.前线轨道理论的预测结果与福井函数极为相符.双描述符的结果相较其它方法稍逊一筹.若改用基于Hirshfeld电荷计算的简缩双描述符函数来考察,则结果会有一定改善.两种基于ALIE的方法虽然在分析方式上有所不同,但结果并无显著差别.若取代基为甲基时,它们的计算结果都没有正确地反映邻位和对位的相对活性大小.

从表2可见,对于含有单个邻对位定位基的取代苯体系,基于静电效应的第二类方法的预测结果整体不理想,平均分显著低于第一类方法,都出现了至少一次完全预测失败的情况.在这些方法中,分子表面静电势极小点分析方法结果最差,并且存在两个主要问题.一个问题是极小点只出现在对位的碳上,这样,既无法正确体现邻位定位效应,也无法讨论邻位反应活性.例如图3(a)所示的苯酚体系.另一问题是极小点往往出现在不合适的位置而导致无法判断哪个位点更可能参与反应.例如对于取代基是O-的情况,极小点恰出现在苯环中心处.而对于苯乙烯,极小点则恰出现在邻位与间位碳之间,以及间位与对位碳之间,如图3(b).若改用环平面上方0.16 nm处的静电势来讨论,结果仍然很不理想.四种计算原子电荷的方法中,Mulliken电荷结果最差,Hirshfeld和NPA电荷的预测能力基本相当.但对于取代基为CHCH2的情况,这三种方法都错误地高估了间位的反应活性,没能正确地预测出邻对位基的定位效应.

表1 第一类预测方法对含有单个邻对位定位基体系的结果及打分aTable 1 Results and scores of the first kind of prediction methods for the systems containing single ortho-para directing groupa

表2 第二类预测方法对含有单个邻对位定位基的体系的结果及打分aTable 2 Results and scores of the second kind of prediction methods for the systems containing single ortho-para directing groupa

4.2 含有单个间位定位基的体系

表3和表4给出的分别是第一类和第二类预测方法用于含有单个间位定位基的体系的预测结果和打分.

相对于邻对位定位基的情况,第一类方法的得分普遍大幅下滑.特别是FF及CFF,虽然它们用于邻对位定位基非常理想,用于间位定位基时却经常完全失败.结果最差的是前线轨道理论,各个测试体系中HOMO分布最大的位点几乎都是在邻位,对于氰基取代的情况则是在对位,完全不能表现出间位定位效应.另外,我们发现,利用HOMO分布来预测活性位点还存在两方面局限性.一方面是HOMO有时主要分布在取代基上而非苯环上,如图4(a)和图4(b)所示的苯甲醛和乙酰苯体系.对这种情况,通过HOMO不可能区分开苯环上不同位点的反应活性高低.另一方面,HOMO和HOMO-1的能量差异有时很小,忽视HOMO-1或更低分子轨道的作用是不合理的.例如苯磺酸的情况,HOMO和HOMO-1的能量分别为-7.837和-7.898 eV,仅相差0.061 eV.

图3 静电势极小点在苯酚(a)和苯乙烯(b)范德华表面上的分布Fig.3 Distribution of electrostatic potential minima on the van der Waals surfaces of phenol(a)and styrene(b)

表3 第一类预测方法对含有单个间位定位基的体系的结果及打分Table 3 Results and scores of the first kind of prediction methods for the systems containing single meta directing group

表4 第二类预测方法对含有单个间位定位基的体系的结果及打分Table 4 Results and scores of the second kind of prediction methods for the systems containing single meta directing group

虽然CDD的结果不理想,但是,通过直接考察双描述符的等值面,可以正确预测出基团的间位定位效应,并且对于一些体系还能正确表现出邻位和对位的活性差异.类似于分子表面静电势极小点分析,分子表面ALIE极小点分析暴露出了同样的问题.由于极小点位置常常不在碳原子附件,干扰了活性位点的判断.例如,对于含有CN、CHO和COCH3基团的体系,ALIE极小点都恰好出现在了邻位和间位碳分界处.若分析方式改为讨论每个原子在苯环上方0.16 nm处的ALIE数值则可以避免这一问题,而且预测结果良好.

从表1和表2列出的邻对位定位基的情况来看,第一类方法明显优于第二类方法.表3和表4列出了两类方法对间位定位基的预测结果.尽管两类方法的预测准确度和可靠性普遍都不很高,整体来看第二类方法还是略优于第一类方法.例如对苯甲腈,第一类方法中只有2个方法预测出活性位点在间位,而第二类方法中则有5个预测正确.由表4看出,第二类方法中表现最好的是pz-pop和NPA电荷,平均分最高,而且最低分也不低于7.对于分子表面静电势方法,由于极值点出现的位置总是不合适,对诸多情况无法作出判断,缺乏使用价值.另一方面,苯环上方0.16 nm处的静电势则可以正确地表现出间位定位效应.Hirshfeld电荷虽然平均分较高,但是对于三氟甲基取代的体系却预测错了.CHELPG电荷和Mulliken电荷对于含间位定位基的体系表现都很差.

图4 苯甲醛(a)和乙酰苯(b)的HOMO电子密度等值面图Fig.4 Isosurface map of electron density of HOMO of benzaldehyde(a)and acetophenone(b)

第一类方法和第二类方法分别适合含有邻对位取代基和间位取代基的情况,展现出一定互补性,这和这两类基团对苯环电子密度的影响有一定联系.邻对位取代基除了卤素等少数外,都表现出给电子特征,增加了苯环上的整体电子密度.尽管卤素电负性大,通过诱导效应能够显著吸电子,但也同时具有给电子共轭效应.在我们测试的含邻对位定位基的体系中,邻位和对位碳的pz轨道布居数都明显大于1.0.间位取代基则完全表现出吸电子特征,明显降低了苯环上整体的电子密度.即便是间位碳,其pz轨道布居数值也都没有超过1.0.苯环上电子越丰富,不仅亲电反应越容易发生,同时电子也越容易极化、转移,软-软相互作用越占主导,而反应的区域选择性对静电效应越不敏感.这是为什么描述局部软度的方法比基于静电效应的方法更适合邻对位取代基的情况.反之,当苯环上电子相对缺乏时,电子云被原子核电荷束缚得较强而不易极化或转移,硬-硬相互作用的地位开始凸显,静电效应就成为了决定反应位点的主要因素,这正是描述静电效应的预测方法在含有间位取代基的情况下表现较好的原因.

4.3 含有双取代基的体系

对于含有双取代基的情况,第一类预测方法的结果列于表5.从平均分来看,所有方法表现较好,特别是CFF和CDD.福井函数、双描述符和HOMO成分分析仅对于C2(4-氯甲苯)结果不佳.其余两种方法,即分子表面ALIE极小点分析以及环平面上方0.16 nm处ALIE数值分析,结果很相似并且多数情况下给出了很满意的预测结果,但是对于C4(3-羟基苯甲醛)却没有正确预测出首要反应位点.

表5 第一类预测方法对双取代苯的结果及打分Table 5 Results and scores of the first kind of prediction methods for disubstituted benzenes

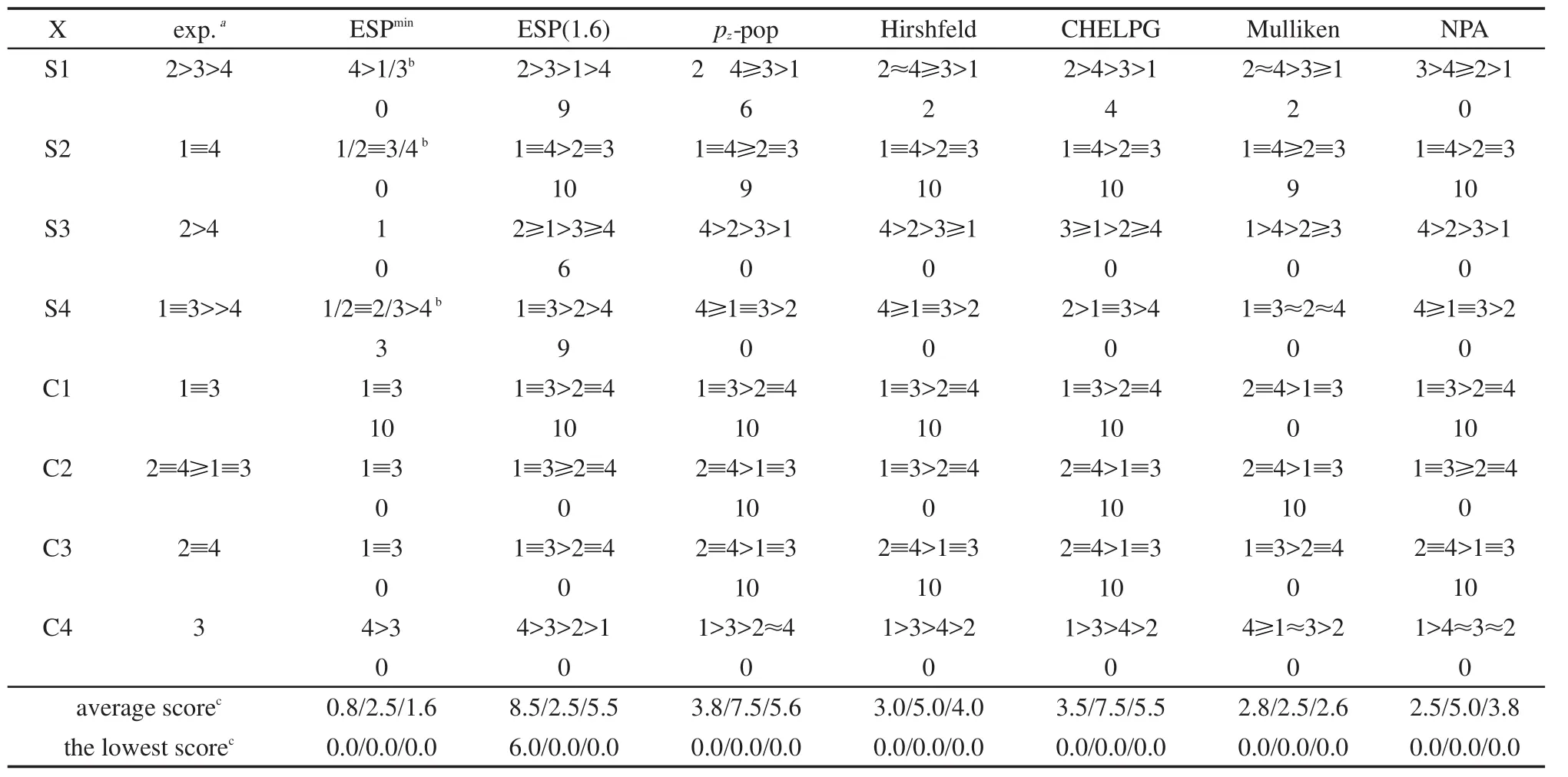
表6 第二类预测方法对双取代苯的结果及打分Table 6 Results and scores of the second kind of prediction methods for disubstituted benzenes

在测试的8个双取代体系当中,S1-S4中的两个取代基的定位效应是协同的,而C1-C4则是冲突的.因此,原则上来说预测后者的位点活性顺序应当更为困难.但是从实际结果来看预测的准确度并无太大差异.

由表6可见,第二类方法整体来说很不适合预测双取代苯的活性位点,平均分都较低,而且每种方法都出现了多个零分.这和测试体系中取代基大部分为邻对位定位基也不无关系.相对而言,环平面上方0.16 nm处静电势分析适合预测定位效应相协同的体系,而pz-pop和CHELPG电荷更适合定位效应相冲突的体系,但整体来看它们都有近一半的体系完全预测失败.表现最差的是分子表面静电势极小点分析,此时已完全没有使用价值,仅对于C1(对甲基苯酚)预测对了反应位点.尽管NPA在原理上与pz-pop有较大关联,但表现明显更差.pz-pop的相对优势在一定程度上表明排除σ电子的影响有助于提高预测能力.

5 结论

预测亲电反应的活性位点具有重要的理论和实际意义.本文系统地介绍了各种常用的亲电位点预测方法的原理,并通过14个单取代苯和8个双取代苯体系对它们进行了测试.得到如下结论:

(1)描述电子局部软度的方法十分适合含有单个邻对位定位基的情况.在这些方法中,福井函数(包括简缩福井函数)表现最好,预测准确度很高.它不仅可以预测邻对位定位效应,通常还可以正确反映出邻位和对位之间相对反应活性的大小.双描述符(包括简缩双描述符)、平均局部离子化能、HOMO轨道成分分析也有很好的预测能力.不过,这类方法大多不适合用于含有单个间位定位基的情况,特别是福井函数此时表现很差,而双描述符却依然适用.

(2)多数描述静电效应的预测方法对于含有单个邻对位定位基的情况表现较差,但对于含单个间位定位基的情况,其表现稍好于描述局部软度的方法.尽管如此,这类方法的准确度和可靠性依然不是特别理想.在这些方法中,pz-pop的表现是最为出色的.尽管CHELPG电荷是通过拟合分子表面静电势得到的,从原理上讲,其对静电效应的表现应该比其它原子电荷更好,但是从活性位点预测能力上看,CHELPG电荷并不占优势.Mulliken电荷是最为常用的原子电荷模型,然而预测能力却非常差,应当避免使用.

(3)对于含有双取代基的体系,描述电子局部软度的方法整体上比描述静电效应的方法明显更可靠.

(4)对取代苯体系,利用分子表面静电势的极小点或ALIE的极小点来分析各位点的反应活性,从实际效果上看,还不如直接比较环平面上方0.16 nm处的静电势和ALIE的数值大小.

(5)综合来看,考察双描述符等值面是最可靠的预测各个位点的反应活性大小的方法.尽管此方法并非总是表现得最好,但对于各种测试体系来说,它至少能正确预测出首要反应位点.

虽然本文讨论的方法只考虑了反应物自身的电子结构,而忽略了亲电试剂特征、位阻效应、溶剂以及反应温度等诸多因素,但是对于当前的测试体系,这些方法对各位点的反应活性顺序仍然给出了较准确的预测.由此看来,这些因素是相对次要的,不是起决定作用的.但是在某些情况下它们的影响将不可忽略,尤其是位阻效应.这就需要对现有预测方法进行适当的改进.这样,改进后的方法不仅能定性预测出不同位点反应活性的次序,还有可能定量地预测出各种产物产率的相对大小.

本文测试体系只考察了取代苯体系,这是亲电取代反应中最简单的一类分子.亲电取代反应还可以发生在杂环及取代杂环体系(如吡咯、吡啶)、多环芳烃及衍生物(如萘、马兜铃酸)、多环且含杂原子的体系(如胞嘧啶).这些体系可能会给预测亲电反应位点的方法带来更大的挑战,我们将在后续工作中进一步检验.另外,不同位点上发生亲电反应的势垒和实验产率必定有密切关系,反应势垒与各种预测方法结果的相关性是很值得研究的问题,我们也将在未来进行考察。

(1) Koleva,G.;Galabov,B.;Kong,J.;Schaefer,H.F.;Schleyer,P.v.R.J.Am.Chem.Soc.2011,133,19094.doi:10.1021/ja201866h

(2) Kong,J.;Galabov,B.;Koleva,G.;Zou,J.J.;Schaefer,H.F.;Schleyer,P.v.R.Angew.Chem.Int.Edit.2011,50,6809.doi:10.1002/anie.201101852

(3) Esteves,P.M.;de Carneiro,M.J.W.;Cardoso,S.P.;Barbosa,A.G.H.;Laali,K.K.;Rasul,G.;Prakash,G.K.S.;Olah,G.A.J.Am.Chem.Soc.2003,125,4836.doi:10.1021/ja021307w

(4) Hadzic,M.;Braïda,B.;Volatron,F.Org.Lett.2011,13,1960.doi:10.1021/ol200327s

(5) Xing,Q.;Xu,R.;Zhou,Z.;Pei,W.Basic Organic Chemistry,2nd ed.;Higher Education Press:Beijing,1993.[邢其毅,徐瑞秋,周 政,裴基础.基础有机化学.第二版.北京:高等教育出版社,1993]

(6) Marx,D.;Hutter,J.Ab Initio Molecular Dynamics-Basic Theory and Advanced Methods;Cambridge University Press:Cambridge,2009.

(7) Jensen,F.Introduction to Computational Chemistry,2nd ed.;John Wiley&Sons:West Sussex,2007;pp 487-492.

(8) Parr,R.G.;Yang,W.J.Am.Chem.Soc.1984,106,4049.doi:10.1021/ja00326a036

(9) Morell,C.;Grand,A.;Toro-Labbé,A.J.Phys.Chem.A2004,109,205.

(10) Murray,J.S.;Politzer,P.Electrostatic Potentials:Chemical Applications.InEncyclopedia of Computational Chemistry;Schleyer,P.v.R.Ed.;John Wiley&Sons:West Sussex,1998;Vol.2,pp 912-920.

(11) Lu,T.;Chen,F.W.Acta Phys.-Chim.Sin.2012,28,1.[卢 天,陈飞武.物理化学学报,2012,28,1.]doi:10.3866/PKU.WHXB2012281

(12) Politzer,P.;Murray,J.;Bulat,F.J.Mol.Model.2010,16,1731.doi:10.1007/s00894-010-0709-5

(13) Murray,J.S.;Politzer,P.WIREs:Comp.Mol.Sci.2011,1,153.doi:10.1002/wcms.19

(14) Politzer,P.;Murray,J.S.Molecular Electrostatic Potentials and Chemical Reactivity.InReviews in Computational Chemistry;Lipkowitz,K.B.,Boyd,D.B.Eds.;John Wiley&Sons:New York,1991;Vol.2,pp 273-312.

(15) Politzer,P.;Murray,J.S.The Electrostatic Potential as a Guide to Molecular Interactive Behavior.InChemical Reactivity Theory:A Density Functional View;Chattaraj,P.K.Ed.;CRC Press:Boca Raton,2009.

(16) Geerlings,P.;Langenaeker,W.;Proft,F.D.;Baeten,A.Molecular Electrostatic PotentialsvsDFT Descriptors of Reactivity.InMolecular Electrostatic Potentials:Concepts and Applications;Murray,J.S.,Sen,K.Eds.;Elsevier Science B.V:Amsterdam,1996.

(17) Politzer,P.;Murray,J.S.;Concha,M.C.Int.J.Quantum Chem.2002,88,19.

(18) Politzer,P.;Laurence,P.R.;Jayasuriya,K.Environ.Health Perspect.1985,61,191.doi:10.1289/ehp.8561191

(19) Sjoberg,P.;Politzer,P.J.Phys.Chem.1990,94,3959.doi:10.1021/j100373a017

(20) Bader,R.F.W.;Carroll,M.T.;Cheeseman,J.R.;Chang,C.J.Am.Chem.Soc.1987,109,7968.doi:10.1021/ja00260a006

(21) Lu,T.;Chen,F.W.J.Mol.Graph.Model.2012,38,314.doi:10.1016/j.jmgm.2012.07.004

(22) Murray,J.S.;Peralta-Inga,Z.;Politzer,P.;Ekanayake,K.;LeBreton,P.Int.J.Quantum Chem.2001,83,245.

(23) Sjoberg,P.;Murray,J.S.;Brinck,T.;Politzer,P.Can.J.Chem.1990,68,1440.doi:10.1139/v90-001

(24) Politzer,P.;Murray,J.S.TheAverage Local Ionization Energy:Concepts andApplications.InTheoretical Aspects of Chemical Reactivity;Toro-Labbé,A.Ed.;Elsevier:Amsterdam,2007;pp 119-137.

(25) Mulliken,R.S.J.Chem.Phys.1955,23,1833.doi:10.1063/1.1740588

(26)Breneman,C.M.;Wiberg,K.B.J.Comput.Chem.1990,11,361.

(27) Weinhold,F.Natural Bond Orbital Methods.InEncyclopedia of Computational Chemistry;Schleyer,P.v.R.Ed.;John Wiley&Sons:West Sussex,1998;Vol.2,pp 1792-1811.

(28) Hirshfeld,F.L.Theor.Chem.Acc.1977,44,129.

(29) Lu,T.;Chen,F.W.J.Theor.Comp.Chem.2012,11,163.doi:10.1142/S0219633612500113

(30)Bader,F.W.Atoms in Molecules:A Quantum Theory;Oxford University Press:New York,1994.

(31) Fukui,K.Theory of Orientation and Stereoselection.InOrientation and Stereoselection;Springer:Berlin,1970;Vol.15/1,pp 1-85.

(32) Lu,T.;Chen,F.W.Acta Chim.Sin.2011,69,2393.[卢 天,陈飞武.化学学报,2011,69,2393.]

(33) Liu,S.B.Acta Phys.-Chim.Sin.2009,25,590.[刘述斌.物理化学学报,2009,25,590.]doi:10.3866/PKU.WHXB20090332

(34)Mohamed Imran,P.K.;Subramani,K.Acta Phys.-Chim.Sin.2009,25,2357.[Mohamed Imran,P.K.;Subramani,K.物理化学学报,2009,25,2357.]doi:10.3866/PKU.WHXB20091131

(35)Yang,W.;Mortier,W.J.J.Am.Chem.Soc.1986,108,5708.doi:10.1021/ja00279a008

(36)Jin,J.L.;Li,H.B.;Lu,T.;Duan,Y.A.;Geng,Y.;Wu,Y.;Su,Z.M.J.Mol.Model.2013,19,3437.doi:10.1007/s00894-013-1845-5

(37) Manzetti,S.;Lu,T.J.Phys.Org.Chem.2013,26,473.doi:10.1002/poc.v26.6

(38) Oláh,J.;VanAlsenoy,C.;Sannigrahi,A.B.J.Phys.Chem.A2002,106,3885.

(39) Pearson,R.G.J.Am.Chem.Soc.1963,85,3533.doi:10.1021/ja00905a001

(40) Yang,W.;Parr,R.G.Proc.Natl.Acad.Sci.U.S.A.1985,82,6723.doi:10.1073/pnas.82.20.6723

(41) Roy,R.K.;Krishnamurti,S.;Geerlings,P.;Pal,S.J.Phys.Chem.A1998,102,3746.doi:10.1021/jp973450v

(42) Domingo,L.R.;Perez,P.;Saez,J.A.RSC Adv.2013,3,1486.doi:10.1039/c2ra22886f

(43) Fuster,F.;Sevin,A.;Silvi,B.J.Phys.Chem.A2000,104,852.doi:10.1021/jp992783k

(44) Lu,T.;Chen,F.W.Acta Phys.-Chim.Sin.2011,27,2786.[卢 天,陈飞武.物理化学学报,2011,27,2786.]doi:10.3866/PKU.WHXB20112786

(45) MacDougall,P.J.;Henze,C.E.Theor.Chem.Acc.2001,105,345.doi:10.1007/s002140000225

(46)Bader,R.F.W.;Chang,C.J.Phys.Chem.1989,93,2946.doi:10.1021/j100345a020

(47) Koleva,G.;Galabov,B.;Wu,J.I.;Schaefer,H.F.,III;Schleyer,P.v.R.J.Am.Chem.Soc.2009,131,14722.

(48) Zhou,Z.;Parr,R.G.J.Am.Chem.Soc.1990,112,5720.doi:10.1021/ja00171a007

(49)Ehresmann,B.;Martin,B.;Horn,A.C.;Clark,T.J.Mol.Model.2003,9,342.

(50) Bruice,P.Y.Organic Chemistry,4th ed.;Prentice Hall:New Jersey,2004.

(51) McMurry,J.Organic Chemistry,7th ed.;Thomson Higher Education:Belmont,2008.

(52) Morrison,R.T.;Boyd,R.N.Organic Chemistry,6th ed.;Prentice Hall,Inc.:New Jersey,1992.

(53)Wang,J.T.;Hu,Q.M.;Zhang,B.Z.;Wang,Y.M.Organic Chemistry,2nd ed.;Nankai University Press:Tianjin,1993.[王积涛,胡青眉,张宝申,王永梅.有机化学.第二版.天津:南开大学出版社,1993.]

(54) Geerlings,P.;Langenaeker,W.;Proft,F.D.;Baeten,A.Molecular Electrostatic PotentialsvsDFT Descriptors of Reactivity.InMolecular Electrostatic Potentials:Concepts and Applications;Murray,J.S.,Sen,K.Eds.;Elsevier Science:Amsterdam,1996;pp 587-617.

(55) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03,Revision B.02;Gaussian Inc.:Wallingford,CT,2003.

(56) Becke,A.D.J.Chem.Phys.1993,98,1372.doi:10.1063/1.464304

(57) Hariharan,P.C.;Pople,J.A.Theor.Chem.Acc.1973,28,213.

(58) Frisch,M.J.;Pople,J.A.;Binkley,J.S.J.Chem.Phys.1984,80,3265.doi:10.1063/1.447079

(59) Hehre,W.J.;Ditchfield,R.;Pople,J.A.J.Chem.Phys.1972,56,2257.doi:10.1063/1.1677527

(60) Multiwfn.http://Multiwfn.codeplex.com(accessed Oct 10,2013).

(61) Lu,T.;Chen,F.W.J.Comput.Chem.2012,33,580.doi:10.1002/jcc.v33.5