舷侧板架与冰体碰撞数值仿真及模型试验研究

张 健，万正权，黄进浩，尹 群

（1江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2中国船舶科学研究中心，江苏 无锡 214082）

舷侧板架与冰体碰撞数值仿真及模型试验研究

张 健1，万正权2，黄进浩2，尹 群1

（1江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2中国船舶科学研究中心，江苏 无锡 214082）

文章利用数值仿真及模型试验两种方法对船体舷侧板架与冰体碰撞进行研究。首先建立了舷侧板架的缩尺比有限元模型，计算冰体碰撞载荷作用下板架结构响应；进而制作了与有限元仿真相同的舷侧板架模型，进行冰体碰撞模型试验，分别获得冰体对板架结构的碰撞力、板架应力分布、板架变形等结果，最后将试验结果与数值仿真结果进行了比较，两者基本吻合。研究结果揭示了冰载荷作用下船体板架结构的响应规律。

冰载荷；船体板架；模型试验；数值仿真

1 引 言

随着北极航道的开发日益受到各国的重视，船—冰碰撞的相关研究逐渐成为国内外学者的研究热点。我国作为近北极的航运大国，北极航线的开辟对于我国航运业的发展具有重大而深远的意义。国外学者针对船—冰碰撞做了一定的研究工作，Gagnon[1-2]等人对冰山碰撞问题同时进行了实验和数值两种方法的研究，在加拿大纽芬兰北部海域实施了冰山碎片与船舶的碰撞试验，然而，由于碰撞能量较小，试验研究中没有提及结构的损伤。挪威科技大学的Liu Zhenhui[3]应用简化的公式来获得船舶与冰山碰撞的能量耗散模式，并对船-冰碰撞进行数值模拟。韩国Lee Sang Gab[4]进行了圆柱形冰体与板架结构的碰撞实验，着重研究了冰体的破坏规律。综上所述，国外学者虽然对钢制结构与冰体碰撞进行过试验研究，但还很不充分。由于我国在这一领域的研究起步较晚，目前的研究成果非常匮乏，针对船-冰碰撞的试验研究更是处于空白状态。本文利用数值仿真及模型试验两种方法对船体舷侧板架与冰体碰撞进行研究，以揭示冰载荷作用下船体板架结构的响应规律。

2 数值仿真研究

2.1 模型尺寸及计算方案

为了与后续的模型试验结果进行对比，船舶舷侧板架根据某油船的舷侧实际结构进行简化及缩尺后得到，缩尺比模型的构件尺寸及板厚根据相似性原理获得。图1为某船实际舷侧板架结构图，取作研究对象的板架结构为方框内部分板架。图2为根据相似性原理缩尺后获得的舷侧板架模型。

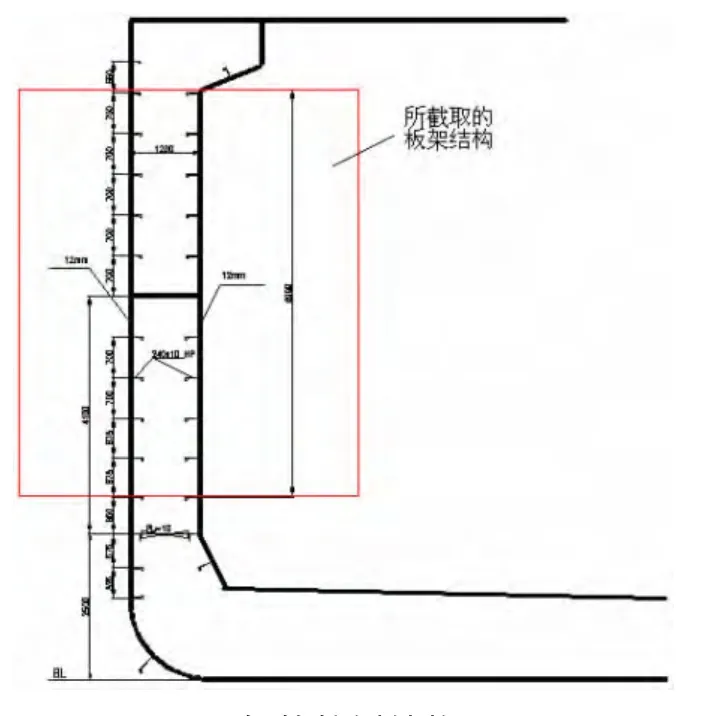
图1 船舶舷侧结构图Fig.1 The figure of ship side structure

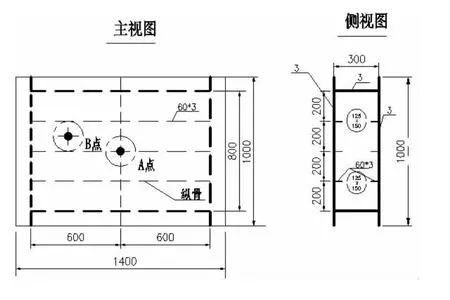
图2 缩尺比舷侧板架结构模型图Fig.2 The reduced scale model figure of side grillage structure

模型尺寸为1 400 mm×1 000 mm的双层板架结构，内外舷之间由两块舷间隔板支撑，舷侧普通肋骨简化为等效厚度，骨架保留水平方向的3根舷侧纵骨及1根竖向的舷侧强肋骨，骨架尺寸根据相似性原理计算得到。

为了探究撞击点位置的不同对板架结构响应的影响，本文进行两种位置处的冰体-结构碰撞有限元数值仿真，冰体质量为60 kg。分别计算冰体碰撞于这两个撞击点时冰体对板架的碰撞力、板架的结构应力、板架的变形量等，A点—强肋骨与舷侧纵骨交叉处，即本模型的几何中心点处；B点—两舷侧纵骨之间的板架中点处，撞击点位置见图2的主视图。

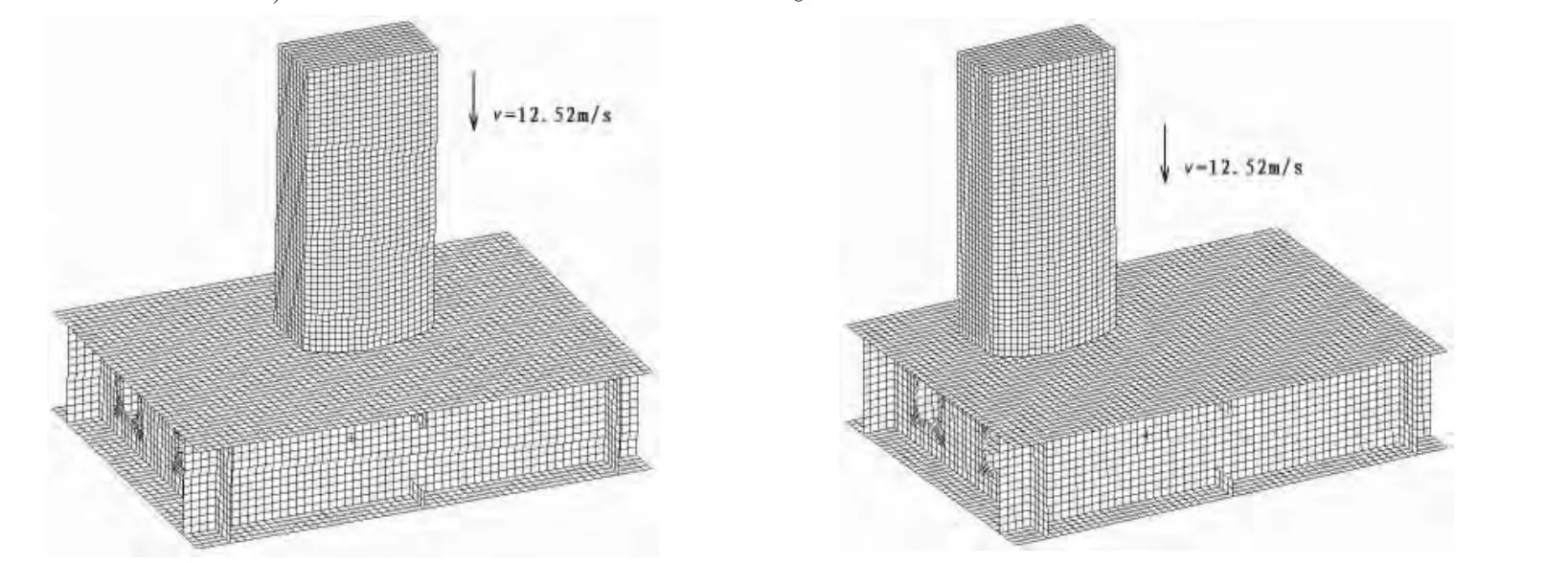
图3 冰体与板架位置关系图Fig.3 Positional relationship between ice and grillage

2.2 有限元模型

冰体模型的长×宽×厚为900mm×400 mm×200 mm，网格大小为20 mm，将冰底部建成圆弧状，目的是减小冰体端面与结构的接触范围。舷侧板架结构网格特征长度为25 mm。模拟冰体从8 m高度处自由落体撞击在板架结构上，此时，撞击速度为v=12.52 m/s，冰体与板架结构的位置关系如图3所示。

2.3 数值仿真计算结果

（1）碰撞加速度

在冰模型的最上方选取一点为输出点，通过仿真计算得出冰在不同撞击位置处的碰撞加速度，计算结果表明，加速度曲线总体趋势波动较为剧烈，A模型的碰撞加速度最大值为2 103 m/s2，而B模型的加速度最大值为1 861 m/s2，均出现在碰撞刚开始的一段时间区间内。

（2）板架结构应力

为便于与试验结果相比较，在有限元模型A上设置与试验时对应相同的编号，编号分别为#1、#6、#7、#8和#9，B模型上同样选取与试验位置相同的5个点，编号分别为#1、#2、#3、#4和#5，如图4所示。

图4 A、B模型上的测点示意图Fig.4 The sketches of test points on models A and B

图5为碰撞后应力云图，图6为两模型数值仿真的应力值比较，从图中可以看出，B模型试验时板架上各点的应力大于A模型试验时各点的应力值，这是因为A、B两点处的板架结构强度不同造成的，较弱的结构产生的应力响应较大，这一结果与A、B两点处的强度差别相吻合。

图5 两模型的应力云图Fig.5 The stress nephograms of two models

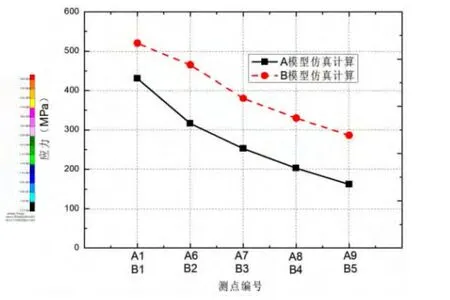
图6 A、B两次碰撞试验各点应力比较Fig.6 The stress comparison with tests of A and B

（3）板架变形

通过仿真计算，得出在A和B两模型的变形云图，见图7，可以看出，变形分布均为从中间往四周逐渐减小。两次数值仿真的各点处的变形值见表1，图8为根据表1数据绘制A、B模型的变形值比较图。

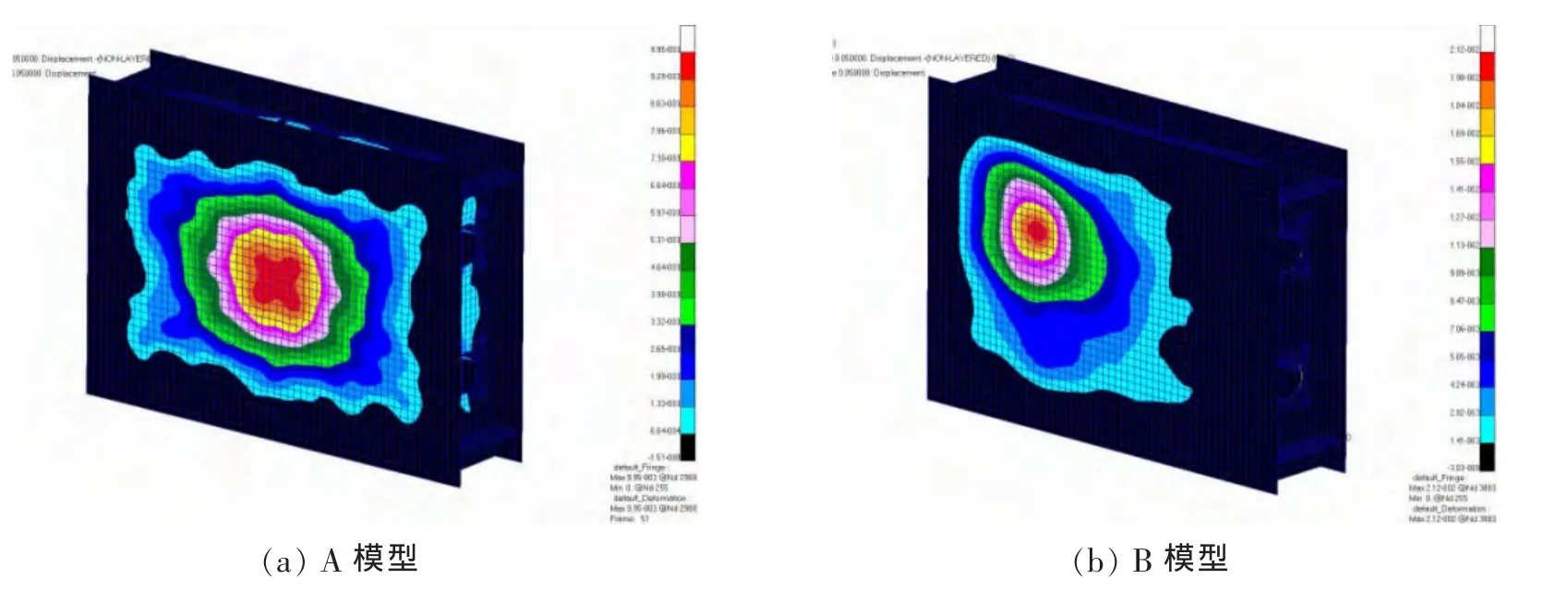
图7 两个板架模型的变形云图Fig.7 The deformation nephograms of two grillage models

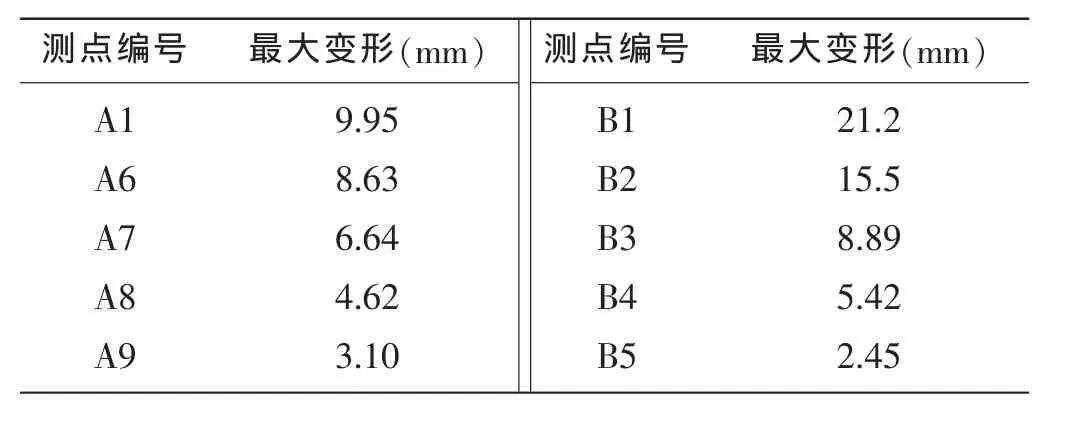
表1 两模型各点处的变形值Tab.1 The deformation value

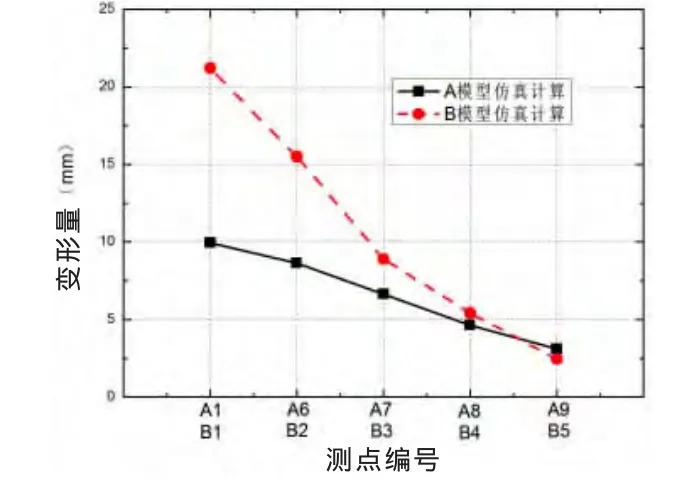
图8 数值仿真变形结果比较Fig.8 The deformation comparison

从图8可以看出，B模型变形量较A模型大，这与B模型撞击点位于板格中心，而A模型撞击点位于板架中心的骨材交叉处结构较强有关。另外，A模型试验中各点的变形量变化基本成线性分布且较为均匀，这是因为A模型的撞击点处有骨架结构，骨架结构的支撑作用可以使整个结构的变形量较为均匀；B模型在第3点处有一定的突变，这是因为B模型的第3点处为骨材经过区域，造成局部的强度提高而使变形量减少。

3 模型试验研究

3.1 试验目的

进行本试验主要测量以下数据：（1）冰体撞击板架结构过程中的加速度变化，进而得到冰体—板架碰撞过程中的碰撞力；（2）碰撞过程中板架结构各部位的应变值，进而计算得到板架结构的应力分布；（3）碰撞试验后板架的变形值。

3.2 试验方案

为了使试验结果与有限元结果具有可比性，模型结构及尺寸与数值仿真所建模型完全一致，模型材料为普通低碳钢Q235，两个完全相同的板架模型分别命名为A模型和B模型。将三向应变片粘贴于模型的舷侧外板的内表面，应变片编号及粘贴位置与数值仿真中的测点一致，见图9，A模型的5只应变片分别为 A1、A6、A7、A8和 A9；B 模型 5只应变片分别为 B1、B2、B3、B4和 B5。 试验所用冰块与数值仿真的冰体尺寸及质量完全相同，冰块自距离板架模型8m的高度自由落体垂直落下，分别撞击A模型中的“A点”及B模型中的“B点”，试验示意图见图10所示。

3.3 试验结果及分析

3.3.1 加速度测量及碰撞力计算

（1）加速度测量及分析

图9 A、B模型的应变片位置示意图Fig.9 Positional sketches of stress section on models A and B

图11 冰体—板架碰撞冰体破碎状态图Fig.11 The ice broken state diagram of ice-grillage collision

图12 冰体与A模型碰撞加速度的时变曲线（0.8 s）Fig.12 The curve of collision acceleration-time under the collision between ice and model A(0.8 s)

不同时刻的冰体破碎状态如图11所示。通过安装在冰体上的加速度传感器测量冰体碰撞A模型过程中的加速度，采样频率0.000 1 s，测量结果如图12所示，该图截取了8.55 s到9.4 s之间共0.85 s的时间区间。

结合试验过程中的高速录像对比分析，可以断定第一次峰值区为冰与板架开始接触即碰撞开始到冰体持续破碎，冰体在破碎过程中加速度产生剧烈变化，第一次峰值区结束后，中间一段加速度几乎为0的阶段是由于后部冰体还未与板架发生碰撞即发生了大破裂，使冰体裂为几块较大体积的冰块，嵌入冰体中的钢棒（加速度传感器安装在钢棒上）从冰体中脱离出来处于短暂的自由漂浮状态，钢棒与冰体分离后不再承受来自冰体的作用力，所以加速度变为0，接下来在9.13 s左右的时刻钢棒在自身重力的作用下掉落在板架上，与板架发生碰撞，由于加速度传感器安装于钢棒上，因而测到了第二次加速度峰值区。B模型的加速度曲线如图13所示，经过与A碰撞模型的对比，发现冰体与B模型碰撞时冰体的最大加速度比A模型碰撞时小。造成该现象的原因，是因为板架上的A点处的结构较B点处强，当冰体分别撞击该点时，较强的结构给予冰体较大的反作用力，致使A点处的最大加速度值较B点大。

综合观察两次碰撞试验的结果，均可发现冰—钢碰撞及钢-钢碰撞不同[5-6]，冰体与板架碰撞除了会在板架上产生碰撞力载荷外，还会对板架结构产生另一种形式的载荷—振动，这是由于冰体的每一次破碎或断裂都会引起与其发生碰撞的结构物上所承受载荷的剧烈变化，这种剧烈变化引起的结构的振动，即为冰激振动，冰激振动效应在海洋平台的立柱与冰体发生碰撞时尤为常见。

图13 冰体与B模型碰撞加速度的时变曲线（0.8 s）Fig.13 The curve of collision acceleration-time under the collision between ice and model B(0.8 s)

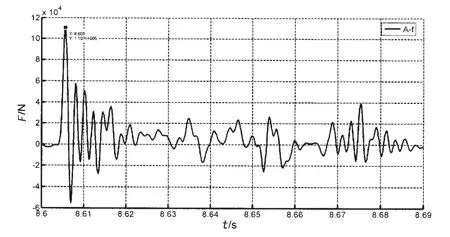
图14 冰体与A模型碰撞时碰撞力的时变曲线Fig.14 The curve of collision force-time under the collision between ice and model A

图15 冰体与B模型碰撞时碰撞力的时变曲线Fig.15 The curve of collision force-time under the collision between ice and model B

（2）碰撞力计算及分析

根据F（t）=m（t）·a（t）的函数关系[6]，计算获得冰体在板架上产生的碰撞力，绘制变化曲线如图14及图15所示。从碰撞力曲线可以发现两个特点：（1）碰撞载荷的瞬时性，碰撞力在碰撞起始时刻最为严重，进而快速衰减。（2）碰撞载荷的振动特性。

3.3.2 应变测量及应力计算

根据试验测得的应变值，即可计算出板架上对应点的Von Mises应力，图16及图17为A、B模型试验中测点的应力变化曲线。从图中可以看出：（1）除个别点外，应力变化趋势基本按照各点到撞击点的距离有规律分布，即由近及远应力依次变小，各个点在碰撞过程中产生的最大应力尤其具有这样的规律，各点的最大应力值见表2。（2）就某一个点随时间的变化情况，可以看出，冰与板架结构碰撞过程中，应力变化与钢结构对钢结构的碰撞不同，结构上的应力在接触瞬间首先产生一个峰值后立刻有较大幅度的下降，然后呈振动形态上下波动，直至碰撞结束，应力才趋于稳定。之所以产生这种现象，是因为碰撞开始的一瞬间冰体重量为最大状态，冰体在碰撞力的作用下迅速而逐渐破碎，重量逐渐下降，冲击力也逐渐下降，因而引起碰撞力随着时间而逐渐下降；应力之所以以振动形态上下波动是由于冰体属脆性材料，而且冰体的失效是不均匀的，碰撞开始初期，接触碰撞使得碰撞力瞬时升高，在巨大碰撞力的作用下冰体中最先接触到板架的那一部分首先产生破碎，冰体破碎给予后面的冰体一部分向下运动的自由空间，因而造成了短时间的卸载现象，在惯性作用下，随着后面冰体的继续向下运动，未破碎的冰体继续对板架产生冲击，因此使得板架上的应力再一次升高，如此反复，形成了板架上上下波动的应力分布曲线，随着冰体破碎殆尽，应力值最终基本趋于平稳。

图16 A模型各点处的Mises应力曲线Fig.16 The curve of Mises stress at each point of model A

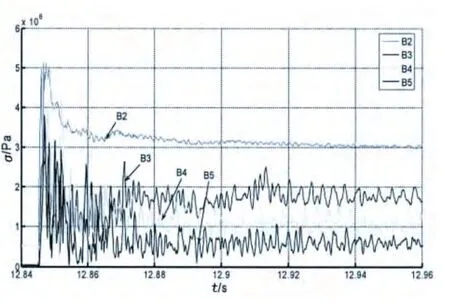
图17 B模型各点处的Mises应力曲线Fig.17 The curve of Mises stress at each point of model B

3.3.3 变形测量结果及分析

测量各个测点处的变形值，结果列于表3及表4中，从表中可知，两个模型中变形最大值均发生在撞击点处，变形量变化的规律都由撞击点向周围呈辐射状渐减，A模型最大变形量为1.21 cm，B模型最大变形量为1.60 cm，该结果与数值仿真结果具有相同的规律且数值基本吻合。因为B模型的撞击点较A模型的撞击点处的结构弱，虽然A点处测得的撞击力较B点大，但是由于结构强度的差别，仍然导致B点处有较大的变形量，说明在冰体与板架结构碰撞过程中，和船-船碰撞一样，撞击点处结构的强弱仍是导致变形量大小的根本原因。利用MATLAB对数据进行处理，获得板架变形三维模拟图，见图18。

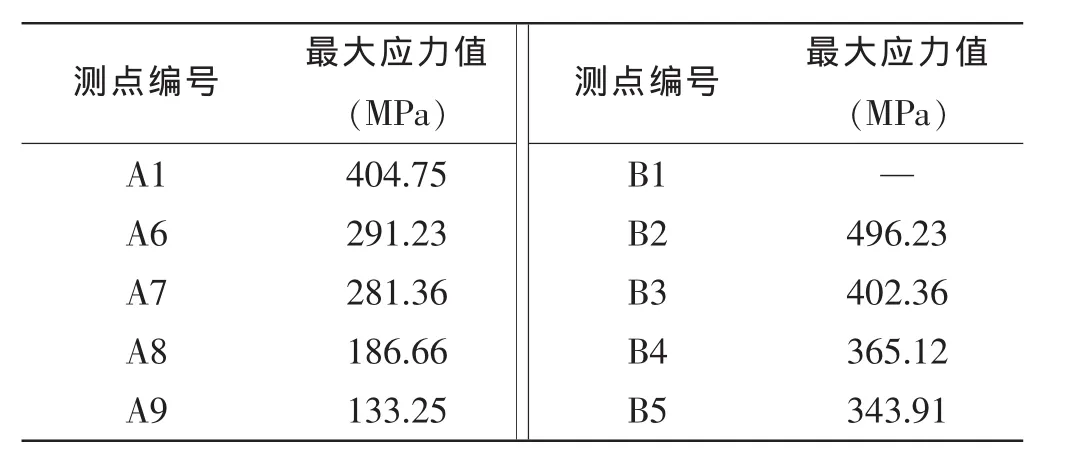
表2 两次碰撞试验各点处的最大应力值Tab.2 The maximum stress at each point of two collision tests

表3 冰体碰撞后A模型变形值（注：A6、B5为碰撞中心点）Tab.3 The deformation value of model A after ice collision(A6 and B5 are collision center points)

表4 冰体碰撞后B模型变形值（注：C5、D5为碰撞中心点）Tab.4 The deformation value of model B after ice collision(C5 and D5 are collision center points)

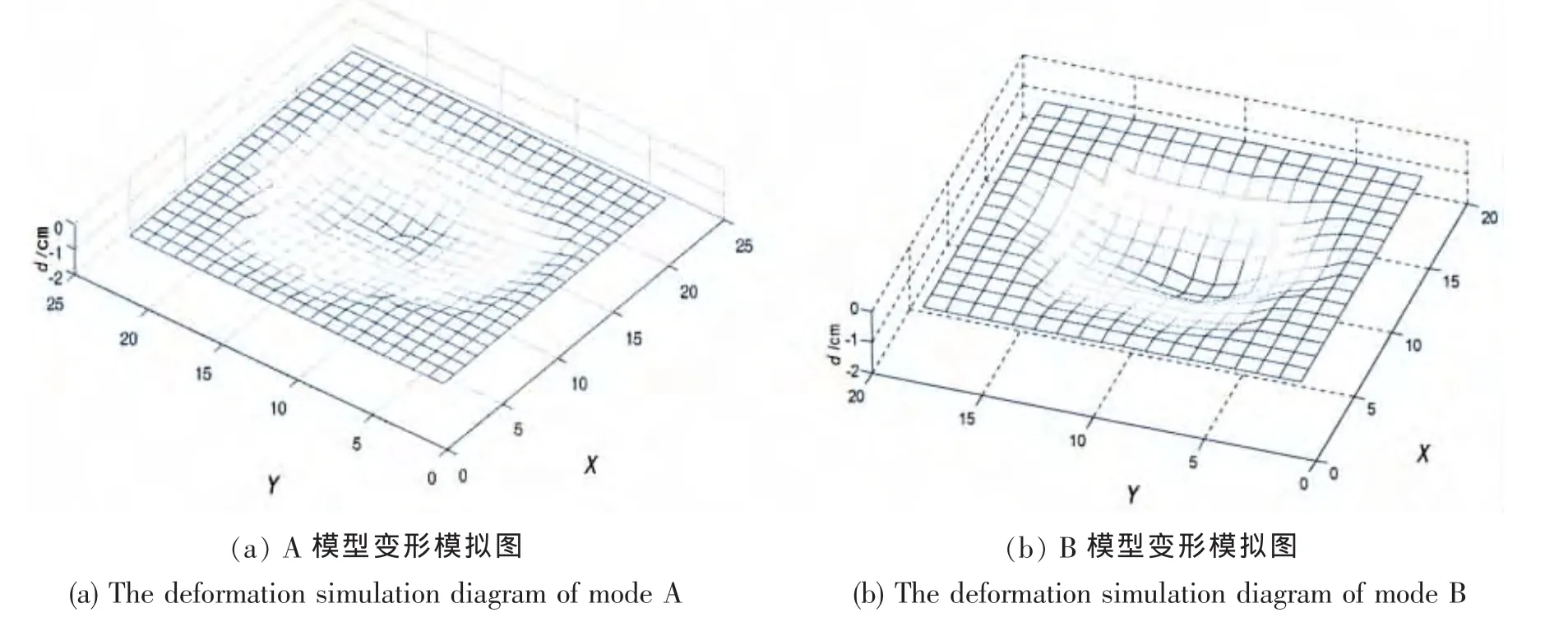
图18 碰撞试验变形三维模拟图（放大6倍）Fig.18 Three-dimensional simulation diagram of the collision test deformation(magnify 6 times)

4 数值仿真及模型试验结果比较

4.1 最大加速度比较

数值仿真及模型试验的加速度最大值比较见表5，可以看出，两种研究方法所得结果比较吻合，但数值仿真结果较模型试验结果略大。分析其原因，主要是因为数值仿真与模型试验涉及的因素较多，再加上数值仿真过程中所建立的冰体模型为理想材料模型，势必会导致两者之间存在一定的误差，误差约为15%，尚在可接受范围。

表5 数值仿真及模型试验的加速度最大值比较Tab.5 The comparison for the maximum acceleration value of numerical simulation and model test

4.2 应力值比较

比较A模型及B模型上对应点处的应力值，如图19所示。

A模型中数值仿真及试验值的最大误差为21.5%，最小误差为6.5%；B模型中数值仿真及试验值的最大误差为16.6%，最小误差为5.47%。产生误差的可能原因主要有两个：一是试验所用的冰体材料与数值仿真所建立的冰体材料模型存在一定的力学性能的差异，温度、凝结方式、水质、凝结时间、内部杂质、气泡等诸多因素均会对试验所用的冰体的力学性能产生影响，而数值仿真模型是理想的冰体材料；二是试验过程中利用应变片测量应变过程中存在系统误差，进而导致计算得到的应力产生误差，应变的误差是因为模型在建造过程中本身存在残余应力以及应变片的测量精度等原因造成的。

图19 数值仿真及模型试验的应力结果比较Fig.19 The comparison for the stress of numerical simulation and model test

4.3 变形量比较

根据前文获得数据绘制数值仿真及模型试验变形曲线，如图20所示。

图20 数值仿真及模型试验的变形量结果比较Fig.20 The comparison for the deformation of numerical simulation and model test

从图20中可以看出，利用数值仿真方法和模型试验方法得到的A、B两个模型的变形规律是一致的，即都以撞击点为中心向外围变形量逐渐减小，这一规律在A模型中更为明显，因为A模型的撞击点为板架正中心，同时也是结构的对称中心，冰体撞击到舷侧下部的交叉骨架后，骨架整体变形，形成较为规则的凹陷。由于B模型中的撞击点位于两个骨材中间的板格中心，在受到撞击后板格中心的钢板变形明显，在向外围扩展过程中遇到骨材的约束，因此，使其变形规律发生变化，形成沿板格方向较长的凹陷、板格宽度方向较小的凹陷。利用两种方法获得的变形最大值虽然存在一定误差，但尚可接受。

5 结 论

利用数值仿真及模型试验两种方法对冰-板架碰撞进行研究，并对两种结果进行比较。可以得出如下结论：

（1）模型试验所获得的碰撞加速度、板架结构应力、板架变形等结构响应与数值仿真结果具有同样的规律及趋势，且数值吻合较好，两者相互验证，说明利用数值仿真方法进行船-冰碰撞结构响应研究的可行性。

（2）冰—板架结构的碰撞模型试验及数值仿真计算结果表明，冰—钢碰撞与钢—钢碰撞产生的结构响应不同，冰-钢碰撞产生的碰撞力曲线总体上呈振动衰减形态，冰体除了对板架形成碰撞瞬时冲击力载荷外，冰体的破碎还会对结构产生振动载荷。

（3）通过对A、B两个模型的碰撞试验结果的比较，不同的碰撞位置对船体板架的加速度、最大应力、最大变形量等结构响应的影响明显，这主要与不同位置处的结构强度差异有关。

[1]Gagnon R.Analysis of laboratory growler impact tests[J].Cold Region Science and Technology,2011,39(1):1-17.

[2]Gagnon R.First results of numerical simulations of bergy-bit collisions with the CCGS terry fox icebreaker[C]//Proc.of the 18th Int.Ass.for the Hydo-Enviroment Eng.and Research(IAHR)on Ice,Aug.28-Sep.1,2006.Sapporo,Japan,2006.

[3]Liu Zhenhui,Amdahl J,Løset S.Integrated numerical analysis of an iceberg collision with a foreship structure[J].Marine Structures,2010,22(2):1-19.

[4]Lee Sang Gab,Lee J S,Baek Y H,Paik J K,Kim B J.Structural safety assessment in membrane-type CCS in LNGC under iceberg collision[C].ICSOT 2009:Ice Class Vessels.Busan,Korea,2009.

[5]Liu Junjie,Wan Zhengquan,et al.Numerical simulations of the damage process of double cylindrical shell structure subjected to an impact[J].Journal of Ship Mechanics,2010,10(6):660-669.

[6]朱新阳.潜艇典型结构在撞击载荷作用下动态响应的试验研究[J].船海工程,2009,38(4):88-91.

Research on numerical simulation and model test of collision between side grillage and icebergs

ZHANG Jian1,WAN Zheng-quan2,HUANG Jin-hao2,YIN Qun1

(1 School of Navy architecture and Ocean Engineering,Jiangsu University of Science and Technology,
Zhenjiang 212003,China;2 China Ship Scientific Research Center,Wuxi 214082,China)

Both numerical simulation and model test method were carried out to research the collision between side grillage and icebergs.The finite element model of side grillage considering scale factor was built,the response of grillage structure under ice load was calculated;and then the same entity of side grillage as the finite element model was made,iceberg collision test was conducted,the results such as impact force,strain and deformation of grillage model were obatined respectively,Finally,The results of model test and numerical simulation are compared,the two agreed basicly.The response law of grillage structure under ice load is revealed by research results.

ice load;hull grillage;model test;numerical simulation

U661.4

A

10.3969/j.issn.1007-7294.2014.04.010

1007-7294（2014）04-0424-10

2013-12-08

江苏省船舶先进设计制造技术重点实验室开放研究基金（CJ1206）；江苏省高校优势学科建设工程资助

张 健（1977-），男，博士，江苏科技大学船舶与海洋工程学院副教授，E-mail:justzj@126.com；

万正权（1962-），男，中国船舶科学研究中心研究员，博士生导师。