基于非线性有限元法的橡胶隔振器构型优化

刘文玺，周其斗

（海军工程大学 舰船工程系，武汉430033）

基于非线性有限元法的橡胶隔振器构型优化

刘文玺，周其斗

（海军工程大学 舰船工程系，武汉430033）

设计一种用于连接两板的橡胶隔振器。以Mooney-Rivlin模型为基础，对橡胶材料进行静态特性的试验研究，得到了材料模型参数。根据实际的使用要求，设计隔振器的参数、基本尺寸，以此为基础，采用优化计算法，以隔振器的尺寸、预紧力、两板间距、橡胶的最大应力为变量，以隔振器刚度为目标，同时，满足隔振量的要求，用非线性有限元法进行数值计算，得到满足要求的隔振器。

构型优化；Mooney-Rivlin；橡胶隔振器；非线性有限元法

1 引 言

在一些海洋结构物（如潜器等）内部，有些声学装置、电声器件被安放在甲板或平台板上[1]，为了避免无关的外界振动的干扰，常要采取一些隔振措施，在甲板或平台板下面安放隔振器，隔振器的下端与基座板相连，这样使得平板及其上面的设备整体隔振，如图1所示；一些小型的水下结构物，为了减弱动力设备工作时引起的结构振动对其他舱室的仪器和设备的干扰，可以将动力设备所在的一段舱室的两端用多个隔振器与这段舱室两端的其他结构相连，这样使得两端的其他舱室得到整体的隔振效果，如图2所示。

图1 平板及其上面设备的整体隔振Fig.1 Vibration-isolation of the plate and machines

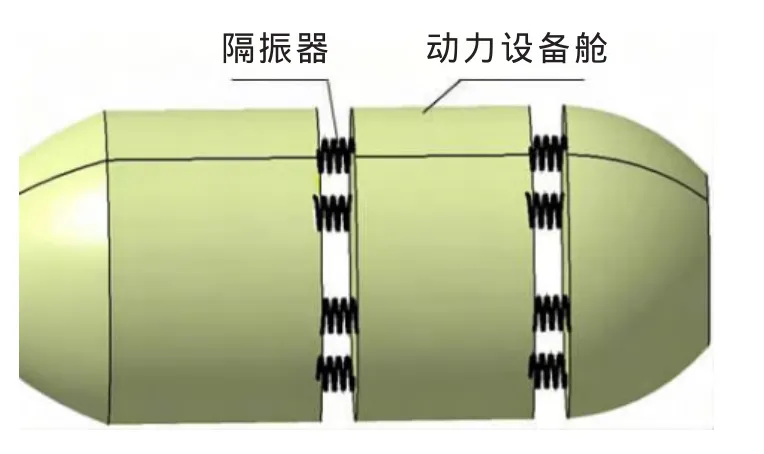
图2 舱室的整体隔振Fig.2 Vibration-isolation of the cabin

工程实际中，需要满足类似于上述隔振效果的情况还很多，为了达到上述隔振目的，设计一种用于连接两板的隔振器，本文将其称作板间隔振器，这种隔振器由橡胶件与金属件组装而成，用螺栓将隔振器与被连接板固定在一起，有如下特点：

（1）结构简单，占用的空间小；

（2）板间隔振器结构考虑安装拆卸的方便，橡胶弹性元件与金属件不要粘接在一起，同时，橡胶弹性元件采用统一的结构以方便备件的存储和更换；

（3）安装板间隔振器时，螺栓施加预紧力的大小应使隔振器工作时被连接板、金属垫片与弹性元件不脱开，弹性元件之间也不发生分离；

（4）两块板通过板间隔振器连接在一起，一块板的振动经过弹性元件的衰减传递到另一块板，达到隔振的目的；

（5）一般情况下，隔振器的结构、材料很复杂，其性能只有通过试验才能确定，而板间隔振器的性能可以通过数值计算的方法确定，缩短了设计周期，降低了成本。

根据板间隔振器的上述特点和实际的使用要求，设计隔振器。以Mooney-Rivlin模型为基础，对选用的氯丁橡胶材料进行静态特性的试验研究，得到了材料模型参数。设计隔振器的参数、基本尺寸，以此为基础，采用优化计算法，以隔振器的尺寸、预紧力、两板间距和橡胶的最大应力为变量，以隔振器刚度为目标，同时，满足隔振量的要求；由于板间隔振器安装时会产生较大的变形，橡胶材料是非线性的，应按大变形计算，因此采用非线性有限元法进行数值计算，得到满足要求的隔振器。

2 橡胶材料的弹性常数及试验测定

氯丁橡胶弹性较好，因此，在橡胶隔振器设计中，优先选择氯丁橡胶，本文板间隔振器的设计中，采用该种橡胶。

取邵氏A硬度70的氯丁橡胶（40%的氯丁和60%的烟片胶），由国际橡胶硬度等级与杨氏弹性模量间的关系[2]，小变形时的杨氏弹性模量E≈6 MPa，泊松比ν≈0.5，基本上为体积不可压缩。

由于板间隔振器安装时产生较大的变形，应按大变形计算。

橡胶是一种各向同性的体积近似不可压缩超弹性材料（外力做功与变形路径无关的弹性材料称之为超弹性材料），超弹性材料的特征是存在一个应变能函数W，其非线性弹性本构模型可以用应变能函数描述[3]，

式中：σ是Cauchy应力张量，p是静水压力，I是单位矩阵，B是Cauchy-Green变形张量，其三个应变不变量是

对于不可压缩橡胶材料I3=1，W=W（ I1, I2）是应变能函数，目前得到广泛承认并在工程中大量应用的是Mooney-Rivlin模型，其应变能函数表达式如下：

式中：C10和C01为Mooney-Rivlin系数，由材料试验数据拟合确定，与小变形下（初始状态）的弹性常数间有如下关系：

式中：μ，K分别为剪切弹性模量和体积弹性模量，它们与杨氏弹性模量E和泊松比ν有如下关系：

由橡胶拉伸试验[4-6]可以得到应力—应变曲线，通过曲线拟合得到Mooney-Rivlin材料参数C10、C01分别为C10=0.499 7 MPa，C01=0.451 7 MPa，橡胶材料的体积弹性模量由试验测定是很困难的，若不知道体积模量，可假定其为 1 400 MPa，由此通过（4）式得 d=1.43×10-31/MPa。

3 板间隔振器设计计算

3.1 隔振器的参数设计

在进行隔振器的具体设计之前，根据使用要求，设计隔振系统的动刚度、静刚度[7-8]和隔振器的基本结构。

根据前述的板间隔振器的特点和使用要求，初步设计了板间隔振器的基本结构形式，如图3所示。

本文设计的隔振器沿竖直方向安装，连接板2在下面，是基座板，固定在其它结构上；连接板1在上面，板1及其上面的设备被整体隔振，只通过隔振器与连接板2相连接，且满足下面的要求：

（1）根据安装空间，隔振器的外径不超过150 mm，高度不超过75 mm；

（2）隔振器的内径大小应满足在正常工作状态下，橡胶件与螺杆不接触；

（3）位移或力的传递率小于0.3；

（4）作用在上板的激振力频率大于40 Hz，隔振系统的固有频率小于激振力频率的二分之一，即小于20 Hz；

（5）隔振器的橡胶件与金属件均满足强度要求。

图3 板间隔振器的基本结构形式Fig.3 Basic structure of the rubber isolator

在螺栓预紧力的作用下，隔振器产生预紧变形。在预紧状态下，连接板1上受到正弦扰动力F=F0sin（ ωt）的作用，隔振系统做小幅振动，系统固有频率fn（角频率 ωn=2πfn），阻尼比 ζ，通过隔振器作用在基座板上力F′=F0′sin ω（）t，对于这一弹性安装的隔振系统来说，动力传递率TA表示为

由前述可知，TA＜0.3，所以由（7）式及隔振系统的固有频率小于20 Hz的要求，系统固有频率fn取18.6 Hz，连接板1及其上面设备总质量M=100.4 kg，因此，整个隔振系统的垂向动刚度Kd=M（ 2π fn）2=1 364.9 N/mm，根据经验，动刚度大约是静刚度的1.3～1.5倍，这里，静刚度取Ks=Kd/1.3=1 050.0 N/mm

3.2 板间隔振器结构优化设计和刚度特性数值计算

数值计算的过程是通过优化计算[9]确定隔振器的形状和尺寸，使隔振系统的刚度等于设计值。由于板间隔振器安装时产生较大的变形，橡胶材料是非线性的，应按大变形计算，因此采用非线性有限元法进行数值计算。

优化设计按如下三步进行：

（1）优化计算，确定静刚度：计算在螺栓预紧状态下隔振系统的静刚度。以橡胶件外径Dout、内径Din、预紧力Fpre、橡胶件沿垂向的压缩率ε和两个连接板间距Ldis为变量，以隔振器静刚度值为目标，同时，满足橡胶、金属的强度要求，用非线性有限元法进行数值计算，得到满足要求的隔振器。在计算模型中，橡胶元件与金属件之间通过接触关系连接，通过接触算法来确定它们之间的关系[10]；

（2）计算隔振系统垂向振动固有频率；

（3）计算隔振系统垂向动刚度值。

一般地，动刚度值与设计值会有差异可采取如下措施进行修改：首先，保持动刚度值不变，调整静刚度值，或者动刚度值和静刚度值均保持不变，然后，根据差异情况，调整预紧力大小和隔振器尺寸，重复步骤（1）到（3）的计算，直至得到满意的结果。优化设计的过程如图4所示。

将图3所示的板间隔振器的基本结构形式优化后，得到如图5所示的优化结构形式，其中（i）是隔振器数值计算的有限元模型，（ii）表示是隔振器详细尺寸，（iii）是橡胶弹性元件。

图4 板间隔振器优化设计过程Fig.4 Process of the optimizing design of the tween plate isolator

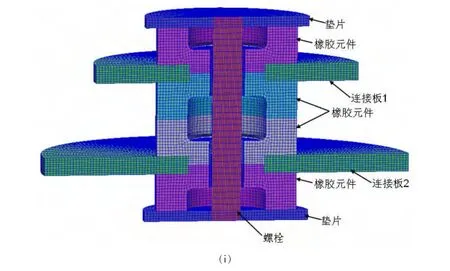
图5 板间隔振器的优化结构形式Fig.5 Optimizing structure of the rubber isolator

经过上述的优化计算可知，螺栓的预紧载荷为4 400 N，隔振器垂向预紧变形为8.8 mm，弹性元件整体的压缩率达8.8%，在预紧状态下，连接板1上受到垂向静载荷是983.7 N，连接板1在整个加载历程中的垂向位移如图6所示，其中，预紧力加载的时间历程是横轴的0～1.0，垂向静载荷加载的时间历程是横轴的1.0～2.0，在垂向静载荷作用下，两连接板之间的垂向相对位移为0.958，板间隔振器在垂向静载荷作用时的垂向静刚度为：Ks=983.7/0.958=1 026.8 N/mm。

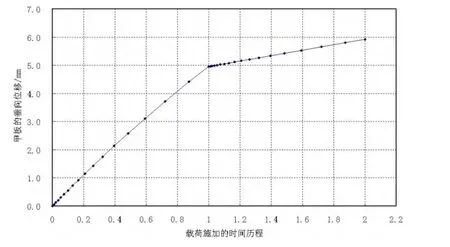
图6 连接板1在整个加载历程中的垂向位移Fig.6 Vertical displacement of the upper plate during loading

隔振器固有频率的设计值是18.6 Hz，计算隔振器在预紧状态下的固有频率，得到隔振器的垂向振动一阶固有频率是17.8 Hz，振型图如图7所示。

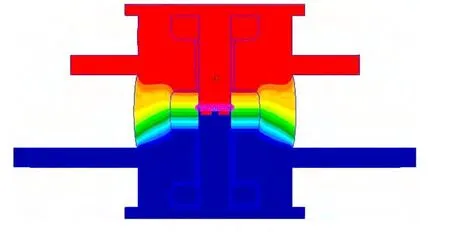
图7 隔振器垂向振动一阶振型图Fig.7 First-order natural frequency vibration model of isolator in vertical direction

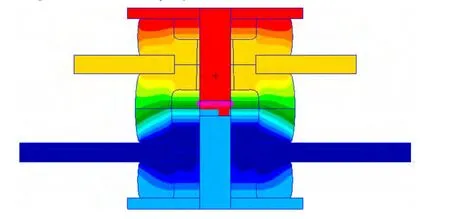
图8 板间隔振器在预紧力、垂向静载荷作用下的变形图Fig.8 Deformation of the isolator under the action of preload and vertical static load

图9 板间隔振器在预紧力、垂向静载荷作用下的VON MISES应力云图Fig.9 Von Mises stress fringe of the isolator under the action of preload and vertical static load

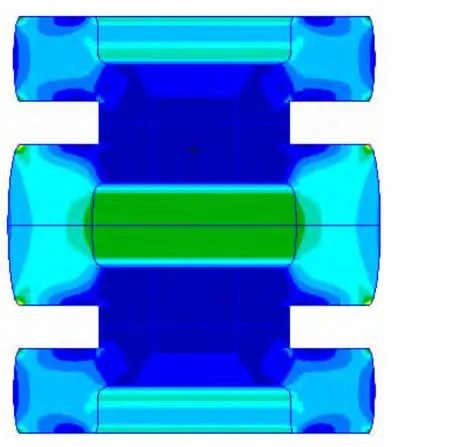
图10 板间隔振器在预紧力、垂向静载荷作用下橡胶件的Von Mises应力云图Fig.10 Von Mises stress fringe of the rubber under the action of preload and vertical static load

由动刚度 ，而Kd=M（ 2π fn）2，而fn=17.8 Hz，因此隔振系统动刚度Kd=M（ 2π fn）2=1 250.0 N/mm，与设计值相差不大。

图11 板间隔振器在预紧力、垂向静载荷作用下橡胶件与金属件的接触状态Fig.11 Touching state between rubber and metal component under the action of preload and vertical static load

板间隔振器在4 400 N的预紧力和983.7 N垂向静载荷作用下的变形如图8所示。Von Mises应力云图如图9所示，钢的最大Von Mises应力为112.0 MPa，橡胶的应力远小于钢的应力，橡胶的Von Mises应力云图如图10所示，最大应力为2.89 MPa，出现在接触的角点处。钢材的屈服极限是590 MPa，氯丁橡胶的屈服极限是15～20 MPa，因此计算结果满足强度要求。

板间隔振器在预紧力、垂向静载荷作用下橡胶件与金属件的接触状态如图11所示，其中高亮显示的区域表示接触，可以看出，橡胶件与垫片、钢板一直处于接触状态，且基本上没有滑移，与螺栓不接触，最大间隙距离为2.0 mm。

4 结 论

（1）从计算结果可以看出，本文设计的板间连接隔振器满足设计的要求，能够正常工作，隔振器工作时被连接板、金属垫片与弹性元件不脱开，弹性元件之间也不发生分离。

（2）对于橡胶金属隔振器，用文中所提出的基于非线性有限元法的优化设计方法，可以实现通过数值计算的方式进行设计，缩短了设计的周期，提高了效率。

[1]朱石坚,何 琳.船舶机械振动控制[M].北京:国防工业出版社,2006:20-59.

[2]张立群.橡胶工程:如何设计橡胶配件[M].北京:化学工业出版社,2002:15-60.

[3]Treloar L R G.The physics of rubber elasticity[M].Third edition.Oxford:Clarendon Press,1975.

[4]林 松,张 鲲.橡胶隔振器动态特性的本构研究[J].振动冲击,2011,30(3):177-210.

[5]叶 伟,何 琳,等.肘形橡胶软管平衡性能研究[J].船舶力学,2009,13(2):285-289.

Ye Wei,He Lin,et al.Study on equilibrium performance of rubber hose elbow[J].Journal of Ship Mechanics,2009,13(2):285-289.

[6]韩德宝,宋希庚.橡胶隔振器刚度和阻尼本构关系的试验研究[J].振动冲击,2009,28(1):156-160.

[7]闫 辉,姜洪源.金属橡胶隔振器随机振动加速度响应分析[J].物理学报,2010,59(6):4065-4070.

[8]吴礼刚,段小成.半主动液阻型橡胶隔振器动态性能测试与计算分析[J].振动冲击,2011,30(4):33-37.

[9]Li Liangwei,Zhao Yao,Li Tianyun,et al.Parameters optimization of the dynamic absorber to control the axial vibration of marine shafting system[J].Journal of Ship Mechanics,2012,16(3):307-319.

[10]张平豪,吴新跃.基于接触算法的气囊隔振特性分析及简化[J].船舶力学,2011,15(7):799-805.

Zhang Pinghao,Wu Xinyue.Vibrating characteristic analysis and model simlification of air bag based on contact algorithm[J].Journal of Ship Mechanics,2011,15(7):799-805.

Study on configuration optimization of rubber isolator by nonlinear FEM

LIU Wen-xi,ZHOU Qi-dou

(Dept.of Naval Achitecture Engineering,Naval University of Engineering,Wuhan 430033,China)

The Configuration Optimization of tween plate isolator is studied.In order to obtain the model’s parameters,the static characteristics of the rubber are studied experimetally on the basis of the Mooney-Rivlin model.For meeting the requirement of engineering practice,the basic parameters and the basic dimensions are designed,and then an optimization algorithm is adopted for detailing the rubber isolator,in which the dimensions of the isolator,the preload,the distance between the two plates and the maximum stress are considered as the design variables,and the stiffness is considered as the objective function.In the condition of satisfying the vibration-isolation effect,the numerical calculation is made by the nonlinear finite element method(FEM),and the rubber isolator is designed successfully.

configuration optimization;Mooney-Rivlin;rubber isolator;nonlinear FEM

TB535+.1

A

10.3969/j.issn.1007-7294.2014.04.011

1007-7294（2014）04-0434-07

2013-06-01

*****演示验证项目（*2011001/101）

刘文玺（1977-），男，博士后，E-mail:wxliu777@yahoo.com.cn；

周其斗（1962-），男，海军工程大学教授，博士生导师。