潜艇围壳线型优化抑制脉动压力与流激噪声的数值模拟研究

张 楠，吕世金，沈泓萃，谢 华

（中国船舶科学研究中心，江苏 无锡 214082）

潜艇围壳线型优化抑制脉动压力与流激噪声的数值模拟研究

张 楠，吕世金，沈泓萃，谢 华

（中国船舶科学研究中心，江苏 无锡 214082）

潜艇脉动压力与流激噪声的数值预报与分析已经成为流声耦合研究领域的重要课题。文章对于潜艇围壳进行了前缘加装填角以及三维座舱型围壳的线型优化，并采用大涡模拟与声学类比方法对于原围壳、带填角围壳与三维围壳的涡旋流场（马蹄涡）和声学特征进行了数值计算评估，分析了围壳线型优化对于壁面脉动压力和流激噪声的定量影响与抑制效果，研究表明直立型围壳加装填角或者进行三维流线型设计，可以明显改善围壳区域特别是围壳与艇体交接部的流动品质，使得脉动压力与流激噪声显著下降。文中工作有益于潜艇流声耦合学术研究以及未来新型潜艇设计。

围壳；线型优化；马蹄涡；脉动压力；流激噪声；大涡模拟；声学类比

1 引 言

当火箭、飞机、导弹等飞行器在空气介质中运动，或舰船、潜艇、鱼雷等航行体在水介质中运动时，它们的外表面都会形成边界层。边界层内的脉动速度诱导产生物面上的脉动压力（pressure fluctuations或者wall pressure fluctuations），进而产生远场流激辐射噪声。边界层中的脉动压力特性是湍流研究中的基础性问题。由于脉动压力是湍流非定常特性的重要表征，而且是流激噪声的重要来源，所以在流体诱发振动与噪声的许多工程应用问题中脉动压力都备受关注[1-5]。一般认为，在水下噪声问题中，边界层脉动压力的重要性主要表现在两方面[4-5]：第一、它是声纳设备自噪声的主要来源。第二、它激励载体的壁面和其他构件振动，一方面向周围介质辐射噪声，另一方面也在载体内部产生舱内噪声。

由于以上原因，研究湍流边界层脉动压力的特性及其抑制方法具有十分重要的实际意义。在早期，大量有关湍流脉动压力的研究都是在平板边界层或管路边界层中开展的，试验测量是一个主要的研究手段，当时要做到精确的测量也比较困难，主要在于脉动压力对于传感器的形式和尺寸较敏感，而且脉动压力具有非常广泛的时间与空间尺度，目前，由于压力传感器的更新换代，试验研究又有了广泛且深入的进展。

利用数值模拟手段计算壁面脉动压力与流激噪声是当前该领域的研究热点，对于简单几何形式的物体，国外已有应用直接数值模拟的研究，但限于计算条件，多年来进展并不明显，对于复杂几何形式的物体，还是趋向于大涡模拟（LES）方法[6-14]。LES方法本身的特点就在于可以求解非定常的精细湍流特征，这种非定常的内涵是LES与RANS最大的区别。2007年剑桥大学出版社出版了一部由三十位学者合作完成的专著—《声学中的大涡模拟》[15]，在这本书中，作者们明确指出，用大涡模拟方法计算非定常流场，在此基础上，进而计算壁面脉动压力与流激辐射噪声，是大涡模拟方法真正的用武之地。目前，大涡模拟在声学计算中已经崭露头角，将来更要发挥举足轻重的作用。而要建立有工程实用价值的大涡模拟方法，就必须需要可靠的试验数据来做验证，近年来，中国船舶科学研究中心在拖曳水池、低速风洞、循环水槽、低噪声直流小风洞和小型多功能高速空泡水筒中进行了大量湍流脉动压力的模型试验，测试模型涵盖平板、翼型、回转体、小突体等基础模型以及潜艇、舰船、流水孔、声呐罩等实际模型，同时在循环水槽中也进行了大量流激噪声测量，为深入分析湍流脉动压力与流激噪声特性与规律，以及验证CFD数值模拟方法在计算流动非定常特征方面的能力提供了坚实的技术支撑。

潜艇指挥台围壳无疑是潜艇脉动压力和流激噪声的最主要来源之一。潜艇指挥台围壳是一流线型的导流罩，其对那些需要经常接触水面的作战系统起到保护作用，这些被围壳包围在内的作战系统包括：潜望镜、通信天线、通气管设备、声呐阵、舰桥出入舱口、导航设备以及其他装置等。自从上世纪四十年代开始，潜艇围壳形状与尺寸就已基本固定，一直沿用至今，并无根本性改变，其设计思路为：先选择一个低阻力的母型，将所需作战系统全部包围在内，然后不断改型，尽量达到最小体积最小阻力的要求，这种设计约束直接导致翼型围壳的诞生，并首先在美国潜艇上应用，被其他各国沿袭至今。

围壳外型与尺寸对潜艇阻力、流场、脉动压力与流激噪声有重要影响。多年来，为了进一步提高潜艇的水动力性能与噪声性能，人们一直致力于改变围壳外型与尺寸，甚至尝试过移除围壳的探索研究。在早期，围壳外型优化焦点集中在如何降低围壳尾流对潜艇桨盘面入流的影响，改善桨盘面入流品质，进而降低螺旋桨低频线谱噪声。近年来的研究热点集中在如何抑制或消除围壳与主艇体接合部马蹄涡及其所诱发的流激噪声。美国海浪级与弗吉尼亚级潜艇都在围壳前缘加装了填角，流场品质得到很大改善，研究表明在围壳前缘与主艇体结合部加装不同形式的填角对抑制围壳结合部马蹄涡都有较好的作用。近年来，在复合材料和复杂构型技术的支撑下，国外还兴起了研究三维座舱型围壳的热潮，旨在降低潜艇阻力和流激噪声并提高潜艇桨盘面入流均匀性，美国水面武器研究中心的Carderock分部（NSWCCD）致力于潜艇水动力、结构与噪声的综合研究，专门设立了先进围壳研发计划（Advanced Sail Project）[16]，从流体动力、结构强度、水动力噪声、设计技术、复合材料等全方位对三维围壳进行深入研究。

为了加快研究进度并减小设计成本，1997年美国先进潜艇研发部（Advanced Submarine R&D Office）专门成立了CFD计算团队来用数值模拟手段承担三维围壳设计研制中的大量评估问题，支撑项目代号NAVSEA（SEA93R）。迄今为止，这一团队发挥了巨大的作用,节省了大量物理模型试验，并给出了可靠的精细流场与流噪声信息[16]。数值模拟研究主要分两步走，第一步，对于弗吉尼亚级潜艇模型进行系统的阻力、流场和噪声试验，为验证CFD方法提供详细的模型试验数据，利用CFD工具对于上述物理量进行全面模拟，并与试验结果对比，不断改进计算方法，提高计算精度，直到达到设计要求的可接受的计算精度为止；第二步，利用已经验证的CFD方法来指导三维围壳设计，从1998年至今已经进行了大量计算，在此基础上，产生了大尺度模型（LSV1），在实艇制造之前进行相关各项性能的试验验证。LSV1是自主式1/4尺度的海浪级（SSN21）潜艇模型，采用三维围壳，NSWCCD声学研究分部（Acoustic Research Detachment）对此模型进行了大量试验，并利用大涡模拟方法（LES）进行大量计算评估，试验与计算研究表明三维围壳可以显著降低脉动压力和流激噪声。可以讲，目前潜艇线型设计优化重点已经由降低阻力和改善桨盘面流场逐步走向降低脉动压力和流激噪声，数值优化方法也由RANS发展为LES。

脉动压力与流激噪声属于流体力学与声学的学科交叉研究领域，是流声耦合研究的关键所在，近年来，课题组进行了大量系列数值计算[10-14]，目前已基本建立了脉动压力与流激噪声的数值预报方法。在潜艇线型优化与流动控制需求的推动下，本文对于某假想潜艇围壳进行了前缘加装填角以及三维座舱型围壳的线型优化，并采用大涡模拟方法进行了数值计算评估，分析了围壳线型优化对于马蹄涡、脉动压力与流激噪声的定量影响与抑制效果，为新型潜艇的声学设计与水动力设计提供技术支撑。

2 数值模拟方法

2.1 大涡模拟方程

滤波的连续性方程和NS方程可以表示为：

其中：σij为分子粘性引起的应力张量，τij为亚格子应力，需用亚格子涡模型进行模拟：

其中：第一项称作Leonard项，也称作外散射项（outscatter term），代表两个大涡间的相互作用，以产生小尺度湍流；第二项称作交叉项（cross term），代表大、小涡间的相互作用，其间能量可以从大涡向小涡传递，也可以反向传递，从小涡传向大涡，但总体平均起来，能量还是以从大涡向小涡传递为主；第三项称作反散射项或逆散射项（backscatter term），代表小涡间的相互作用以产生大涡，并带来能量从小涡到大涡的传递。过去曾认为，既然各项的物理意义不同，应该分别用不同模型去近似它们，但是由于模化技术尚未完善，分别模化未必准确，所以意义不大，还是倾向于合在一起作总体上的模化[17]。

本文采用动态Smagorinsky模型对亚格子应力进行模拟。这种模型是Germano在1991年提出的[18]，通过动态计算涡粘性系数来尽可能地反映实际流动情况。通过对最小可解尺度的信息进行采样，然后利用这些信息来模拟亚格子尺度应力。此模型在接近壁面边界时给出了正确的渐近特性，而且并不需要阻尼函数或者间歇函数。此模型还能够考虑逆散射的影响。Lilly（1992）[19]利用最小二乘法对此模型进行了改进。详细的公式推导与含义请见文献[11]。

2.2 声学类比方程

Ffowcs Williams与Hawkings声学类比方程，即FW-H方程表达如下：

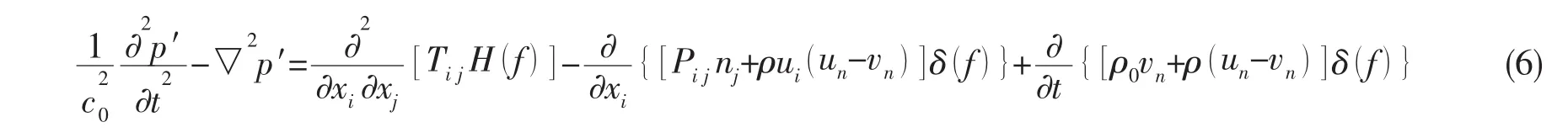
其中：ui为xi方向的流体速度分量；un为垂直于物体表面（f＝0）的流体速度分量；vi为xi方向的物体表面速度分量；vn为物体表面法向速度分量；δ（f）为Dirac delta函数；H（f）为Heaviside阶跃函数。p′为远场声压。f=0表示物体表面，f＞0表示外部无界的自由空间。ni为物面外法线，指向流体内部。c0为远场声速，ρ0为远场密度，Tij为 Lighthill应力张量。

利用自由空间格林函数δ（g）/4πr，可得远场解，本文实际使用的是结合Kirchhoff积分与可渗透表面的渗流FW-H方法。远场声中包含单极子噪声pT′（x,t），偶极子噪声pL′（x,t）以及四极子噪声pQ′（x,t）。

2.3 流激噪声计算特点

Crighton（1988）[22]曾经指出，相对于一般的计算流体力学问题而言，计算流动产生的声要面临更多的挑战。近年来，这一问题又被Colonius与Lele（2004）[23]加以详细地讨论。

首先，产生噪声的流动一定是非定常的，因此不能使用定常计算方法，而非定常的RANS方法又难以达到足够的计算要求，因而对于非定常流动发声问题的模拟而言，应采用诸如DNS、LES、DES这样的现代湍流模拟技术，但它们的计算花费也是巨大的，一般都要在高性能并行计算机上进行。LES和DES都包含不同尺度流动的模拟与近似，这种处理对于流动噪声预报的影响，是一个具有相当理论深度的难题，迄今为止，没人能给出透彻的检验与解释。

其次，流体力学与声学的扰动幅值和特征尺度存在巨大的差异，除了包含激波的高速流动等少数情况之外，只有很小部分的流体能可以在远场转化为声能。在直接方法（CAA）中，声与流动是同时被求解的，这就对数值差分格式有了非常严格的要求。在混合方法（CFD+声学类比）中，流动与声是分别计算的，数值精度也要达到合理的水平，而且所用声源的表达式必须忠实于其实际的辐射特性。

流与声的尺度分离是流动声学中的突出问题，它既带来了计算上的挑战，同时也带来了计算上的简化，关键取决于研究者所选择的方法。在无限区域，声波与流体动力源的时间尺度是相匹配的，其波长λ与源（涡）尺度l之间通过马赫数M而近似表达为λ＝l/M。在水中低马赫数流动中，M＜＜1，这就产生了l与λ之间的巨大差异，使得直接计算声变得十分困难。另一方面，尺度上的巨大差异却使混合方法成为合理而简便的实用方法，即假设声能很小，难以对流体运动产生有效的影响，所以可以先解算出流动信息，然后再代入声学方程解算出声。

2.4 边界条件

速度入口：潜艇首部向前2L，设定来流速度的大小与方向。

压力出口：潜艇尾部向后4L，设定相对于参考压力点的流体静压值。

壁 面：潜艇外表面，设定无滑移粘附条件。

外 场：距潜艇表面约2L，速度为未受扰动的主流区速度。

其中：L指潜艇长度。声学边界处理方法取自文献[20]。

2.5 数值求解

时间项采用二阶隐式格式离散，动量方程采用限界中心差分格式离散，压力速度耦合采用SIMPLE算法。利用代数多重网格方法加速收敛。计算中时间步长Δt=1×10-5s。壁面y+≈1。采用FFT结合Hanning窗处理非定常信号时间序列。

Hanning窗表达式为：

本文所用FFT算法简述如下：

设x（n）为N点序列，N为2的整数次方（4，8，16，……，1 024，……），将序列按偶数点与奇数点分解为两个N/2点的序列：

这样分组后，计算过程变为先计算两个N/2长度的序列DFT，然后求其线性组合。后两个公式表示了一种蝶形运算的流程。分组后的计算量大约是N2/2次复乘，比原来减少一半。分组后的两部分，还可再各自分为两组进行类似的简化，最后分解到每组只有两个点为止。计算量大为减少，计算效率大为提高。上面介绍的FFT算法是对序列分解到只有两个点，逐级采用蝶形运算，故又称为以2为基的FFT算法。为了提高计算速度和减少所需存储容量，人们还研究了其他基以及混合基的各种算法，其中被公认为有效的快速算法是由Winograd提出来的，该算法是将点数N分解为互为质数的因子的乘积，该算法效率高、效果好，本文就采用这种算法。

3 计算方法验证

验证算法所用计算模型为用于基础性研究的围壳，长约2 m。对于水速V=6 m/s的脉动压力与流激噪声进行了计算，基于围壳长度雷诺数为Re=1.2×107，并将计算结果与试验结果对比，验证了计算方法有效性。计算网格与脉动压力测点位置见图1。流激噪声已折算为等效声源级，全计算域都采用结构化网格离散，网格总数为9.6×106。水中参考声压pref_water=1×10-6Pa。本文所有算例都是在无锡超级计算中心采用并行计算完成的，总的计算时间为2个月。

图1 模型表面网格与脉动压力传感器位置Fig.1 Mesh on model surface and position of sensor

图2 w1点脉动压力计算与试验对比Fig.2 Comparison of computed pressure fluctuations with measurement(w1)

图3 w2点脉动压力计算与试验对比Fig.3 Comparison of computed pressure fluctuations with measurement(w2)

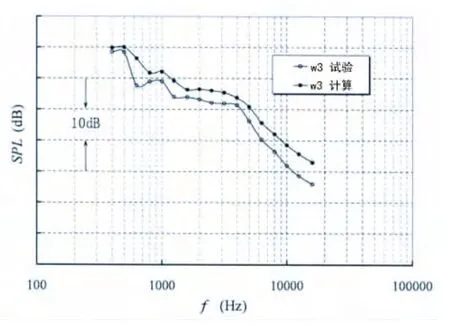
图4 w3点脉动压力计算与试验对比Fig.4 Comparison of computed pressure fluctuations with measurement(w3)

图5 w4点脉动压力计算与试验对比Fig.5 Comparison of computed pressure fluctuations with measurement(w4)

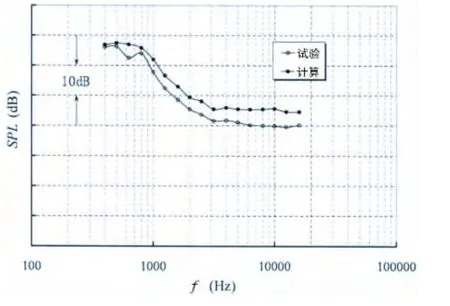
图6 流激噪声计算与试验对比Fig.6 Comparison of computed flow induced noise with measurement

围壳表面四个测点位置的湍流脉动压力计算结果与试验结果的对比见图2～5。首先，从谱型来看，计算得到的脉动压力谱型与试验吻合，随频率增加，脉动压力衰减明显；其次，从幅值来看，在测试频率范围内，计算误差在2～6 dB之内，高频计算误差比低频计算误差大；最后，计算分析总声级可知，围壳脉动压力总声级计算误差在1.5～3.2 dB之内。综上所述，围壳脉动压力计算结果是可靠的。

流经围壳的三维流动会产生宽带噪声，涡旋的形成与演化以及其与壁面的相互作用是流动辐射噪声产生的根源，请见文献[14]。图6给出了围壳流激噪声计算与试验对比。首先，从谱型来看，计算得到的流激噪声谱型与试验吻合，随频率增加，噪声降低，8 kHz以上，谱型趋于稳定无明显变化；其次，从幅值来看，在测试频率范围内，计算误差在3～6 dB之内，高频计算误差比低频计算误差稍大；最后，计算分析总声级可知，围壳流激噪声总声级计算误差为3.1 dB。综上所述，围壳流激噪声计算结果与试验结果也是吻合较好的，这也证明数值计算方法是可靠的。

4 围壳线型优化计算结果分析

本文针对某假想潜艇的直立型围壳进行线型优化，首先设计了前缘带填角围壳与三维座舱型围壳，以期用这些措施来消弱结合部马蹄涡并抑制脉动压力，然后采用已经过验证的大涡模拟方法计算三种类型围壳的涡流场，主要研究马蹄涡的变化情况，同时分析了直立型围壳、前缘带填角围壳与三维座舱型围壳对于壁面脉动压力和流激噪声的定量影响，评估了线型优化效果。各围壳模型主尺度与网格数见表1。计算模型表面网格划分与8个脉动压力采样点位置见图7，三个围壳上采样点相对于主体的位置相同，其上的脉动压力变化情况具有可比性。模型主体长L≈5 m，取水速V=6 m/s，模型长度雷诺数为 Re≈3.0×107。

图7 模型表面网格与脉动压力传感器位置Fig.7 Mesh on model surface and position of sensor

表1 围壳模型主尺度与网格数量Tab.1 Characteristic of fairwater model and number of cell

4.1 马蹄涡计算结果分析

三种围壳与主体结合部马蹄涡计算结果见图8，图中涡面是利用Q涡判据表达的等涡面（Q=3 000），Q取其他数值不改变三种围壳马蹄涡之间的相互关系。

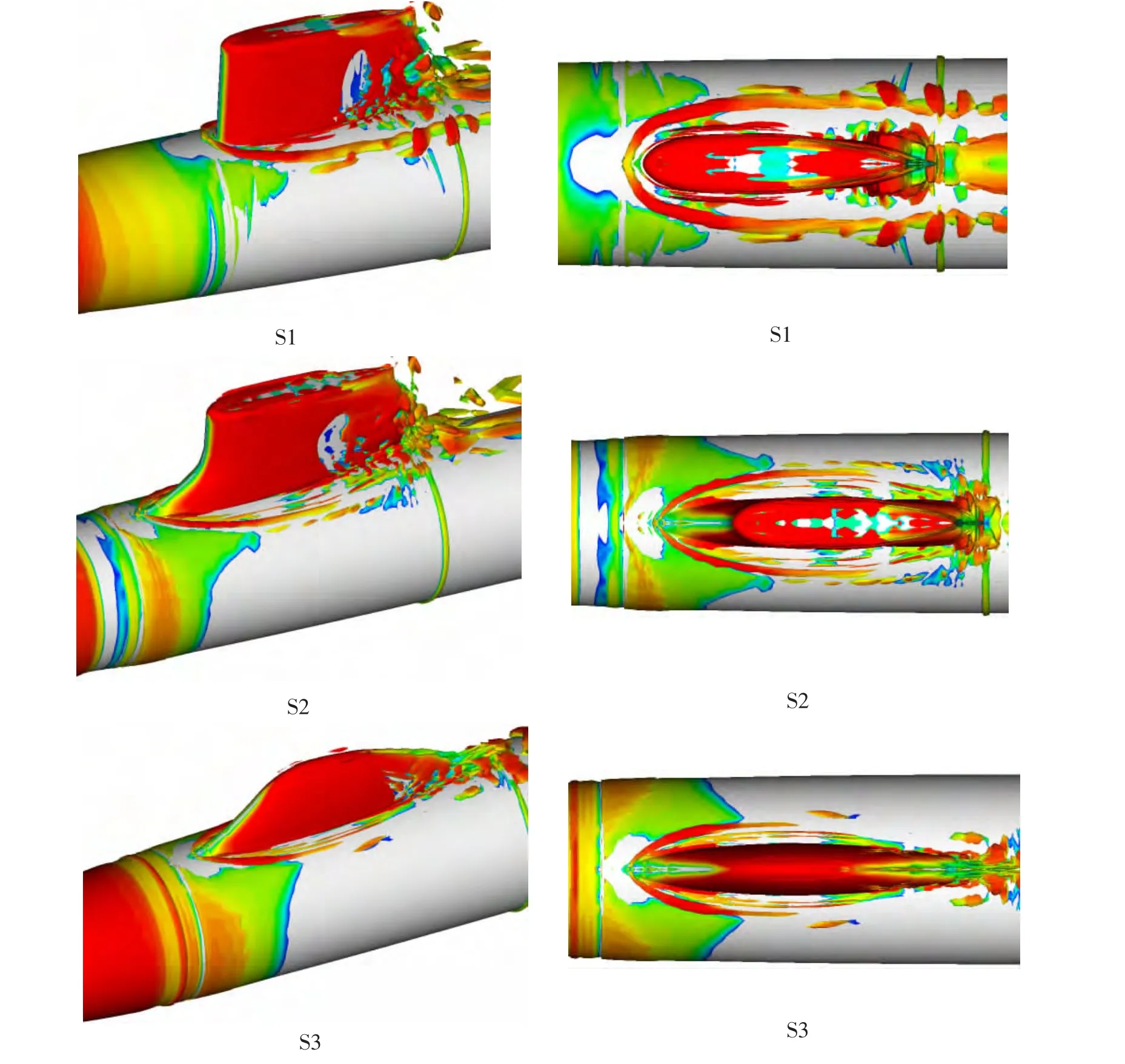
图8 三种围壳与主体结合部马蹄涡计算结果Fig.8 Computed horse-shoe vortex around three fairwater models

从图8可知，原方案直立型围壳马蹄涡呈现明显的“U”型结构，在向围壳下游发展的过程中涡面保持稳定且耗散较慢，能够维持到围壳尾流之中，马蹄涡的涡腿是“粗壮”的，而且通过计算发现其表面上的脉动压力幅值较大；围壳加装填角之后，填角起到了很好的导流作用，与原方案相比，马蹄涡明显得到弱化，涡腿比原方案缩减很多，且马蹄涡在向围壳下游发展的过程中涡面耗散较快，文献[21]曾指出填角能够将近壁面高涡量流动向外排挤和抬升，从而起到抑制涡旋作用，其表面上的脉动压力幅值比原围壳有所减小；三维座舱型围壳对马蹄涡的抑制作用最为明显，与原方案相比，马蹄涡显著得到弱化，涡腿比原方案缩减很多，马蹄涡的涡腿是最为“纤细”的，且马蹄涡在向围壳下游发展的过程中涡面耗散最快，其表面上的脉动压力幅值最小。综上所述，直立型围壳加装填角或者进行三维流线型设计，可以明显改善围壳区域流动品质，使得马蹄涡得到有效抑制。

4.2 脉动压力计算结果分析

三种围壳表面8个采样点位置上的脉动压力三分之一倍频程计算结果见图9。由图可知，与原方案围壳相比，带填角围壳与三维座舱型围壳的脉动压力频谱幅值都有不同程度的下降，而且首部P1、P5两点下降最多，频谱低频段比高频段减幅更明显。围壳加装填角之后，P1点脉动压力降低1～26.7 dB，P2点降低1～11.5 dB，P3点脉动压力降低2～10.7 dB，P4点脉动压力降低1～8.8 dB，P5点脉动压力降低1～31.5 dB，P6点脉动压力降低1～16.6 dB，P7点脉动压力降低2～24.4 dB，P8点脉动压力降低1～3.8 dB；三维座舱型围壳与原围壳相比，P1点脉动压力降低1～25.6 dB，P2点降低1～17.5 dB，P3点脉动压力降低1～21.6 dB，P4点脉动压力降低2～22.5 dB，P5点脉动压力降低2～31.8 dB，P6点脉动压力降低 1～14.8 dB，P7点脉动压力降低 5～25.9 dB，P8点脉动压力降低 1～27.8 dB。

经计算12.5 Hz～10 kHz频段内三种围壳脉动压力总声级可知，与原方案围壳相比，围壳加装填角之后，脉动压力总声级下降2～14 dB，三维围壳使得脉动压力总声级下降2～21 dB。这说明，围壳的优化设计改善了流动特征，弱化了马蹄涡，从而收到了抑制脉动压力的良好效果。

图9 不同围壳表面脉动压力计算结果对比Fig.9 Comparison of computed pressure fluctuations of three fairwater models

4.3 流激噪声计算结果分析

在流激噪声计算中，声压接收器取在远场，然后将计算结果折算为距离等效声中心1 m处的声源级，再进行不同围壳之间的相互比较。计算得到的三分之一倍频程声源级见图10。由图可知，与原方案围壳相比，带填角围壳与三维座舱型围壳的流激噪声频谱幅值都有不同程度的下降，在100 Hz～1 kHz频段，带填角围壳下降2～7 dB，三维座舱型围壳下降 3～9 dB；在 1 kHz～10 kHz频段，带填角围壳下降1～8 dB，三维座舱型围壳下降2～5 dB。经计算100 Hz～10 kHz频段内三种围壳流激噪声总声级可知，与原方案围壳相比，围壳加装填角之后，流激噪声总声级下降4 dB，三维围壳使得流激噪声总声级下降6 dB。计算方法在前面章节得到验证，三个算例的计算精度基本相同，降噪效果为三个围壳之间相互比较的结果，应是可信的。

综上所述，直立型围壳加装填角或者进行三维流线型设计，可以明显改善围壳区域流动品质，使得脉动压力总声级与频谱幅值以及流激噪声总声级与频谱幅值都显著下降。

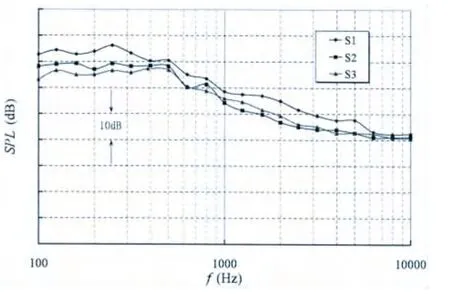
图10 不同围壳流激噪声计算结果对比Fig.10 Comparison of computed flow induced noise of three fairwater models

5 结 语

利用数值模拟方法来对潜艇进行优化设计已是近年来的研究热点。在潜艇线型优化与流动控制需求的推动下，作者从抑制马蹄涡并降低脉动压力与流激噪声的优化目的出发，对于潜艇围壳进行了前缘加装填角以及三维围壳的线型优化，并采用大涡模拟方法对于原围壳、带填角围壳与三维座舱型围壳的涡旋流场与壁面脉动压力以及流激噪声进行了数值计算评估，分析了围壳线型优化对于脉动压力与流激噪声的定量影响与抑制效果，研究表明直立型围壳加装填角或者进行三维流线型设计，可以明显改善围壳区域流动品质，使得马蹄涡得到有效抑制，并使得脉动压力总声级与频谱幅值显著下降，围壳加装填角之后，脉动压力总声级下降2～14 dB，三维围壳使得脉动压力总声级下降2～21 dB，围壳加装填角之后，流激噪声总声级下降4 dB，三维围壳使得流激噪声总声级下降6 dB。本文可为未来新型潜艇的声学设计与水动力设计提供技术支撑。另外，脉动压力与流激噪声的研究属于流体力学与声学的交叉领域，开展相应的理论分析、模型试验和数值计算研究是十分必要的，研究脉动压力与流动发声之间的定量关系是今后重要发展方向。

[1]Blake W K.Mechanics of flow-induced sound and vibration[M].Academic Press.INC,New York,1986.

[2]Ross D.Mechanics of underwater noise[M].Peninsula Publishing,Los Altos,California,U.S.A.,1987.

[3]Skelton E A,James J H.Theoretical acoustics of underwater structures[M].Imperial College Press,1997.

[4]汤渭霖.水下噪声学原理[G].上海交通大学讲义,2004.

[5]朱锡清.船舶流体动力噪声原理[G].无锡:中国船舶科学研究中心讲义,2006.

[6]Chisachi Kato,Yoshinobu Yamade et al.Numerical prediction of sound generated from flows with a low Mach number[J].Computers&Fluids,2007,36:53-68.

[7]Khalighi Y,Mani A,Ham F,Moin P.Prediction of sound generated by complex flows at low Mach number regimes[G].Center for Turbulence Research,Stanford University,Annual Research Briefs 2008,2008:313-324.

[8]Ask J,Davidson L.A numerical investigation of the flow past a generic side mirror and its impact on sound generation[J].Journal of Fluids Engineering,2009,131:061102-1～061102-12.

[9]Gand F,Deck S.Flow dynamics past a simplified wing body junction[J].Physics of Fluids.2010,22:115111.

[10]Zhang Nan,Shen Hongcui,Yao Huizhi.Numerical investigation of the flow induced noise of submarine[C]//8th International Conference on Hydrodynamics(ICHD2008).Nantes,France,2008:591-599.

[11]张 楠.孔腔流动和流激噪声机理及耦合计算方法研究[D].无锡:中国船舶科学研究中心,2010.

[12]Zhang Nan,Shen Hongcui,Yao Huizhi.Numerical simulation of cavity flow induced noise By LES And FW-H acoustic analogy[C]//9th International Conference on Hydrodynamics(ICHD2010).Shanghai,China,2010:242-247.

[13]张 楠,沈泓萃,朱锡清,姚惠之,谢 华.三维孔腔流激噪声的大涡模拟与声学类比预报与验证研究[J].船舶力学,2010,14(1-2):181-190.

Zhang Nan,Shen Hongcui,et al.Validation and prediction of flow induced naise of 3-dimensional cavity with large eddy simulation and acoustic analogy[J].Journal of Ship Mechanics,2010,14(1-2):181-190.

[14]张 楠,张胜利,沈泓萃,谢 华.翼/板结合部涡旋流动结构与壁面脉动压力的大涡模拟研究[J].船舶力学,2013,17(7):729-740.Zhang Nan,Zhang Shengli,et al.Large eddy simulation of vortical flow structure and wall pressure fluctuations around wing-plate junction[J].Journal of Ship Mechanics,2013,17(7):729-740.

[15]Wagner C,Huttl T,Sagaut P.Large eddy simulation for acoustics[M].Cambridge,UK:Cambridge University Press,2007.

[16]Stout M C,Dozier D F.Advanced Submarine Sail[G].Carderock Division,NSWC-Technical digest,2011.

[17]刘应中,缪国平.高等流体力学[M].上海:上海交通大学出版社,2000.

[18]Germano M,Piomelli U,Moin P,Cabot W H.A dynamic subgrid-scale eddy viscosity model[J].Phys.Fluids A.1991,3(7):1760-1765.

[19]Lilly D K.A proposed modification of the Germano Subgrid-scale closure method[J].Phys.Fluids A.1992,4(3):633-635.

[20]Brun C,et al.(Eds.)Numerical simulation of turbulent flows&noise generation[M].Springer-Verlag Berlin Heidelberg.2009.

[21]张 楠,沈泓萃,姚惠之.潜艇阻力与流场的数值模拟与验证及艇型的数值优化研究[J].船舶力学,2005,9(1):1-13.

Zhang Nan,Shen Hongcui,et al.Validation of numerical simulation on resistance and flow field of submarine and numerical optimization of submarine hull form[J].Journal of Ship Mechanics,2005,9(1):1-13.

[22]Crighton D G.Goals for computational aeroacoustics[M].In Computational Acoustics:Algorithms and Applications,Amsterdam:Elsevier-North Holland.1988:3-20.

[23]Colonius T,Lele S K.Computational aeroacoustics:Progress on nonlinear problems of sound generation[J].Prog.Aerospace Sci.,2004,40(6):345-416.

Numerical simulation on the effect of fairwater optimization to suppress the wall pressure fluctuations and flow induced noise

ZHANG Nan,LÜ Shi-jin,SHEN Hong-cui,XIE Hua

(China Ship Scientific Research Center,Wuxi 214082,China)

Numerical simulation of wall pressure fluctuations and flow induced noise of submarine has become vigorous in the field of flow-acoustic coupling.The fairwater of a submarine is optimized by two shapes,one is the fairwater with fillet,and another is three-dimensional canopy-like fairwater.Numerical investigation by LES and acoustic analogy is carried out to analyze the vortical flow fields(horse-shoe vortex)and acoustic characteristics of the three fairwaters,and the effect of optimization is studied to describe the quantitative change of pressure fluctuations and flow induced noise.This study shows that the optimization of fairwater is able to improve the flow quality around fairwater especially in the junction of fairwater and hull,and the wall pressure fluctuations and flow induced noise can be suppressed obviously.The work is beneficial to the research in the field of flow-acoustic coupling and the design of the submarine with a new type.

fairwater;shape optimization;horse-shoe vortex;pressure fluctuations;flow induced noise;large eddy simulation(LES);acoustic analogy

U661.3

A

10.3969/j.issn.1007-7294.2014.04.013

1007-7294（2014）04-0448-11

2014-03-04

自然科学基金资助项目（51079133）；江苏省自然科学基金资助项目（BK2010162）

张 楠（1977-），男，博士，中国船舶科学研究中心高级工程师，E-mail:zn_nan@sina.com；

吕世金（1973-），男，中国船舶科学研究中心研究员。