大直径棒材二辊矫直机辊形研究

张 将，马立东，朱 琳，桂海莲，褚艳涛

(太原科技大学 山西省现代轧制工程中心，太原 030024)

随着国内机械工业的发展，对大棒材的需求量逐年增加，同时对其质量要求也将会越来越高，大棒材精整线也将显得越来越重要。二辊矫直机因具有矫直精度高[6]，结构简单的优点已被广泛采用。以往有很多学者对二辊矫直机做了多方面的研究，马立东等[1]利用大型非线性有限元软件对二辊矫直过程进行数值模拟，得到矫直过程棒材对矫直辊作用力随时间的变化规律；杜晓钟等[2]利用共轭旋转曲面原理，分析了线棒材矫直过程中确定矫直辊辊型曲线的解析方法；刘志亮[3]通过对金属变形理论、矫直工艺及矫直机械的设计制造进行深入研究，给出了二辊矫直机辊形参数的确定方法；敖列伟[4]导出了辊型曲线与矫直精度的关系；日比野文雄[7]提出矫直辊辊形是双曲线辊形加圆柱辊；N K Das Talukder[8-9]对二辊矫直过程中的力能参数进行了理论分析；赖兴涛，刘玉文等[10]对棒材与管材矫直辊辊型进行了研究。但这些理论对于小型棒材较为实用，对于大直径棒材来说还难以在实际生产中得到推广。在此，这种设计方法可为理论研究和实际生产提供参考。

本文通过结合实际大直径棒材二辊矫直机的生产状况，将瞬间冲压模型与二辊矫直过程相结合，对矫直辊进行合理的辊形设计，能够为二辊矫直机国产化和实际生产提供指导。

1 二辊矫直机工作原理

二辊辊矫直机工作原理在斜辊矫直理论中独具特点，它对工件的矫直作用不是依靠各辊之间的交错压弯使工件产生塑形弯曲变形，而是依靠一对辊缝内部弯曲曲率的变化而达到，即采用旋转反弯矫直原理，由于圆材的原始弯曲是多方位的，因此，在矫直时要使圆棒材绕轴线旋转，并在旋转的同时能使其反弯程度由小到大，再由大到小连续变化，才能使任何方位的原始弯曲都能得到可靠的反弯矫直，二辊矫直机的作用是强迫圆材在反弯状态下旋转前进，达到矫直的目的[6]。二辊矫直凹凸辊辊形的组成如图1所示，凹凸辊辊形由辊腰、辊腹、辊胸、过渡圆角组成，且关于辊腰的垂直中心线左右对称。

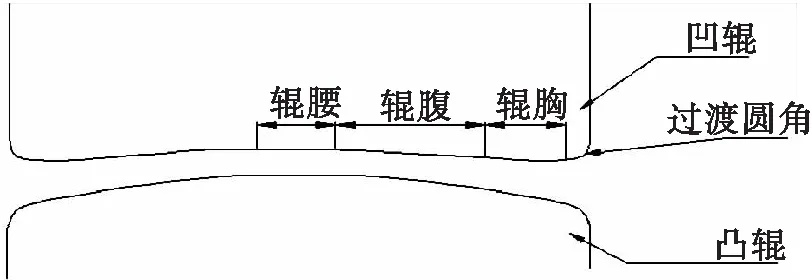
图1 凹凸辊辊形的组成Fig.1 The components of the concave and convex roll-shape

2 大直径棒材二辊矫直机凹凸辊辊形设计

棒材的导程t=πdtanα，其中d为大直径棒材直径(Φ180～Φ300)，α为棒材轴线与凹(凸)辊轴线之间的夹角，一般不超过25°，选取辊身长L≈8t+2q，其中q为凹凸辊辊形末端的过渡圆半径，凹辊辊腰直径Dg1=L/2[6]。

二辊矫直机矫直大直径棒材，其弯曲过程与轧件在冲压模型[5]中的弯曲极为相似，因此，将每一时刻的矫直模型简化为瞬间冲压模型，如图2所示。

图2 瞬间冲压模型Fig.2 The model of instant stamping

结合图1，由图2可以看出：在凹凸辊辊腰处，棒材变形达到最大，但此变形为瞬间最大变形，即棒材在最大变形处的横截面上只有A点变形最大，棒材在螺旋前进过程中依次连续达到最大变形。为了减轻该缺陷对矫直效果的影响，凹凸辊辊形按照以下方法进行设计。

假设在矫直过程中，凹凸辊全身与按规定形状弯曲的棒材全接触[5]，忽略所选截面A(图3)处的棒材断面以及轧辊断面的椭圆半轴差。

二辊矫直机凹凸辊布置形式如图3所示，截面几何如图4所示。

图3 凹凸辊布置图Fig.3 Layout diagram of the concave and convex roll

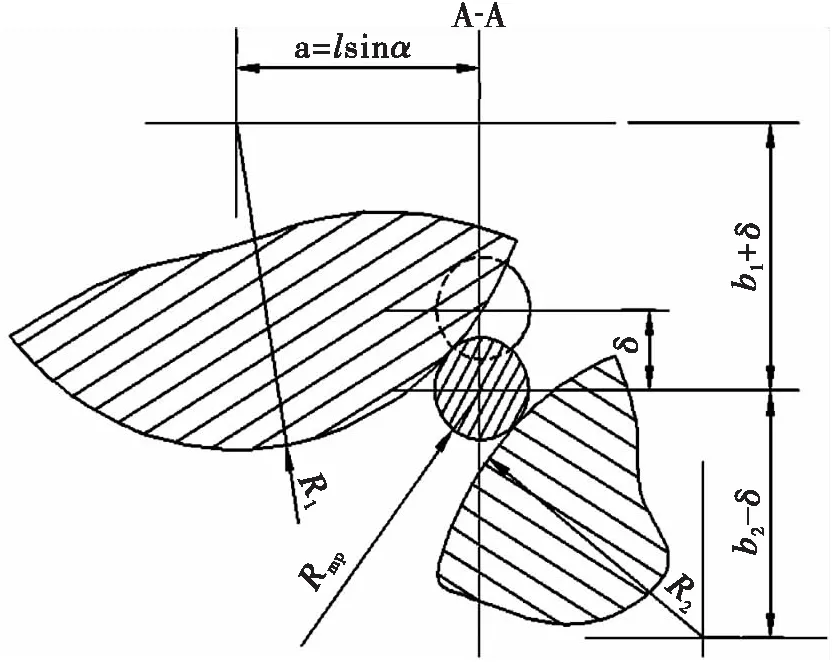
图4 A-A截面Fig.4 A-A section

由图3、图4可得：

(R1，2+Rmp)2≈a2+(b1，2±δ)2

(1)

式中a=lsinα；b1，2=Re1，2+Rmp；Re1，2为凹凸辊辊腰半径；δ为弯曲值；Rmp为棒材的半径。

在此，正号用于凹形辊子1，而负号用于凸形辊2[5]。

于是，凹形辊半径表示为：

(2)

凸形辊半径表示为：

(3)

同理可得出两辊辊边半径分别为：

(4)

(5)

实践证明，在工程精度范围内，可把弯曲的棒材轴线视为圆弧[5]。

设棒材反弯矫直所需的最大曲率半径为ρ[5]，则有：

(6)

为求得最大曲率半径ρ，设棒材原始曲率半径为ρ0，则有：

(7)

式中：E为棒材弹性模量(GPa)，σT为棒材的屈服极限(MPa)，γ为棒材发生反弯后弹性变形量与塑性变形量的比值[5]。

γ与塑性变形深度系数k的关系[5]为：

(8)

各k值得到的γ(k)值如表1[5]所示：

表1 k-γ的对应值Tab.1 Corresponding values of k-γ

则棒材刚好被矫直时所需的反弯曲率为：

(9)

由式(6)-式(9)可求得δmin.

棒材矫直时，若凹凸辊与棒材接触面的转速差较大，这不但会对凹凸辊表面造成严重磨损，还会影响棒材的表面质量。为了减小这些不良影响，取凸辊辊腰直径为：

(10)

结合实际不难发现，在矫直棒材时，正真与棒材接触的是凹辊辊胸与凸辊辊腰处。于是，经过多次模拟测量，最终将凹凸辊辊形设计为分段式。

凹辊：其主要工作段为辊胸，为了使其与凸辊匹配良好，如图5所示，将其辊腰设计成一条水平直线EF，该直线为一个导程长度t；为了尽可能增大辊胸处的接触线长度，使出口处棒材的小变形尽可能一致，现将凹辊的辊胸设计为一段斜直线BC，该斜直线在中心轴上的投影长度为一个导程t；将辊腹设计成一段分别于两端直线相切的一段圆弧CE，该圆弧在中心轴上的投影长度为2.5个导程长度2.5t.最终凹辊辊形由一段水平直线﹑两段圆弧﹑两段斜直线、两个过渡圆角组成。

为了能足够保证矫直质量，经过多次模拟测量总结得出，计算Rk1时：

δ1=2.5δmin

(11)

下面对上述圆弧CE的半径Rc以及斜线BC与圆弧CE相切C点处的辊子半径R求解，其位置关系如图5所示。

已知导程t=m=AC，CE=2.5m=2.5t，凹辊辊腰﹑辊胸半径Re1与Rk1.

设圆弧半径为Rc，其夹角为β，OA长度为y，则由图可求出：OB=Rk1-Re1

设B点坐标为(0，Rk1-Re1)，C点坐标为(t，y)，D点坐标为(3.5t，Rc).

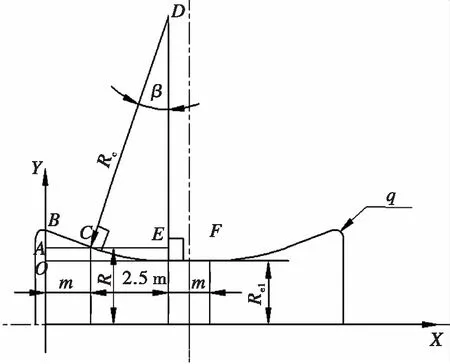
图5 凹辊辊形几何Fig.5 The roll shape geometry of concave roll

由上得出：向量BC=(t，y+Re1-Rk1)，向量CD=(2.5t，Rc-y)

再由BC垂直于CD得出：

BC·CD=(2.5t)2+(y+Re1-Rk1)(Rc-y)=0

(12)

由直角三角形CDE可得出：

(13)

由式(12)、式(13)可求得Rc，y.

此时得出C点凹辊半径R=y+Re1，角度β=arcsin(2.5t/Rc).

辊子端部的过渡圆角半径q取d/2，即棒材半径。

凸辊：为了使棒材上的所有点经过辊腰时，都尽可能得到相一致的大变形，将辊腰处的辊形设计成一条直线bc，其长度为一个导程t；同时为了不影响矫直棒材表面质量，将辊胸与辊腹的7个导程设计成两个相互对称且与直线bc相切的两圆弧ab、cd，如图6所示。凸辊外形可能是凸形也可能是凹形，主要由棒材尺寸﹑材料﹑以及δ的取值等因素决定，但其辊面永远比凹辊面平缓[5]。

最终，凸辊辊形由一段水平直线﹑两段圆弧、两个过渡圆角组成。

同理，用式(4)、式(6)-式(9)求δmin与Rk2时，辊身半长lk取3.5t.

另外，为了能足够保证矫直质量，经过多次模拟测量总结得出，计算Rk2时：

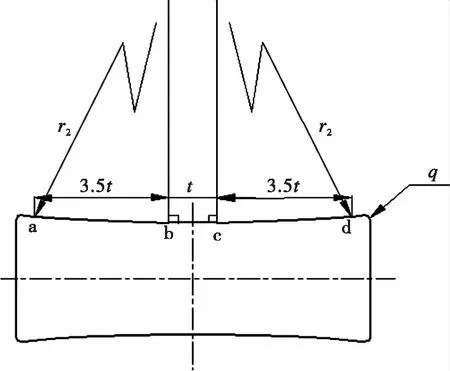
图6 凸辊辊形几何Fig.6 The roll shape geometry of convex roll

(14)

此时，两圆弧半径r2为：

(15)

辊子端部的过渡圆角半径p取d/2，即棒材半径。

3 有限元模拟分析

为了验证上述理论的正确性，利用Abaqus有限元针对Φ180 mm的棒材矫直进行了分析。

棒材材料为45钢，原始挠度为±8 mm/m，常温下σt﹦335 N/mm2，长度为2 m，弹性模量E=210 Gp，棒材轴线与凹(凸)辊轴线之间的夹角α为16°，矫直速度为50 m/min.

棒材矫直前的状态如图7所示，矫直过程如图8所示，矫直后的状态如图9所示。

图7 矫直前的棒材Fig.7 The bar without straightening

在棒材中心线上分别取了四个点，矫直前、后其空间坐标分别如图10、图11所示。

经计算得出其挠度为0.1%，即1 mm/m，满足生产所需要求。

图8 矫直过程Fig.8 The process of straightening

图9 矫直后的棒材Fig.9 The bar with straightening

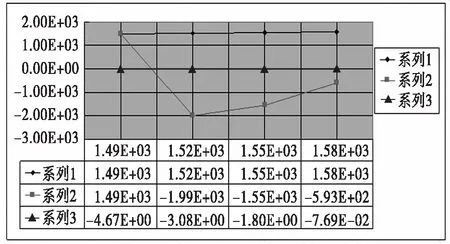
图10 矫直前的点坐标Fig.10 The coordinates of points before straightening

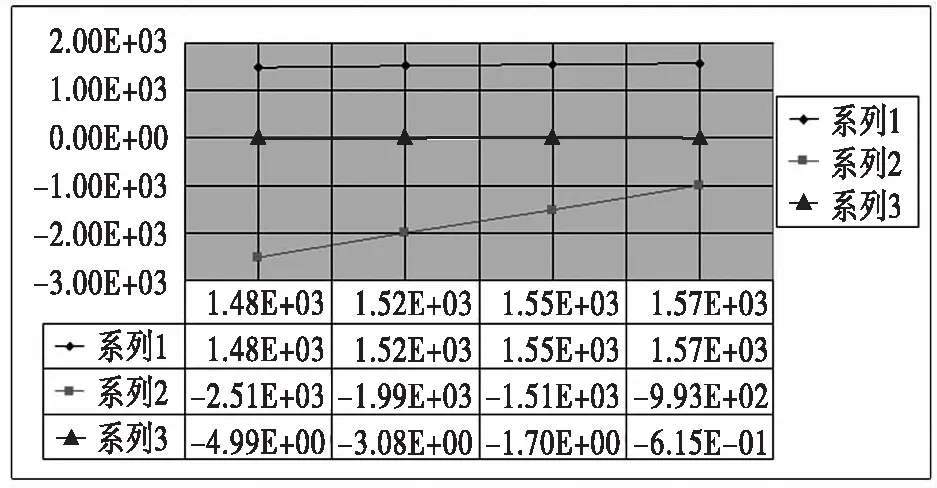
图11 矫直后的点坐标Fig.11 The coordinates of points after straightening

4 结束语

通过瞬间冲压模型与大棒材二辊矫直机矫直过程相结合的理论分析和研究，最终得出一种较为合理的大棒材二辊矫直机辊形的设计方法，该方法可以为大棒材二辊矫直机国产化和实际生产提供指导。

参考文献：

[1] 马立冬，刘才，王云.棒材二辊矫直过程有限元分析及实验[J].塑性工程学报，2012，19(3)：30-34.

[2] 杜晓钟，孙斌煜.共轭旋转曲面法求解线棒材矫直辊型曲线[J].太原重型机械学院学报，2004，25(4)：250-253.

[3] 刘志亮.二辊矫直机辊形参数设计[J].机械设计与制造，2005(6)：25-27.

[4] 熬列伟，吴伯杰，王志成.二辊矫直原理及精度分析.重型机械，1997(6)：41-45.

[5] 马斯基列逊A M.管材矫直机[M].北京：机械工业出版社，1979.

[6] 崔甫.矫直原理与矫直机械[M].2版.北京：冶金工业出版社，2007.

[7] 日本塑性加工工学会.矯正加工——板，管，棒，線た真直すぐにゐ方法[M].日本东京：コロナ社，1992.

[8] DAS TALUKDER N K，SINGH A N.Mechanics of bar straightening，Part2.Straightening in cross-roll straighteners[J].Journal of Engineering for Industry，1991，113(2)：228-232.

[9] DAS TALUKDER N K，SINGH A N.Mechanics of bar straightening，part1.General analysis of straightening process[J].Journal of Engineering for Industry，1993，113(2)：224-227.

[10] 赖兴涛，刘玉文.一种新型的棒材与管材矫直辊辊型的设计方法[J].宝钢技术，2004(6)：36-39.