大型旋转机械转子离心应力有限元分析

0 前 言

组合式转子具有重量轻、刚度大和易冷却等诸多优点，被广泛应用于诸多大型旋转机械中，是旋转机械的心脏。然而，组合式转子结构庞杂，在机组稳态运行过程中，转子离心作用所产生的应力占总应力50%以上，对机组正常运行提出巨大的挑战。目前，国内外学者普遍采用有限元法对此类大型转子的相关问题进行研究，取得了一定的成果。Hamdi T和Blacker T等人运用有限元法计算了转子的应力集中和临界转速；李浦、袁奇等人采用三维有限元非线性接触算法，计算了拉杆转子轮盘在预紧力和扭矩作用下的应力分布。

由于本文所涉及的某大型旋转机械转子非中心对称，结构比较复杂，因此需要建立三维模型进行有限元分析。然而，庞大的三维模型不仅需要巨大的计算资源，而且对于计算精度及收敛性也要求颇高。为解决此类大型设备的高效、精确有限元计算问题，本文以某大型旋转机械转子离心应力有限元分析为例，基于ABAQUS软件，阐述了一种先确定整体模型网格单元密度，后采用子模型精确计算局部应力的方法。

1 三维模型特征去除

图1为某大型旋转机械转子三维模型的剖视，图中，1为转子左端轴头、2为左端轮盘、3为左端鼓桶、4为左端拉杆、5为右端鼓桶、6为右端轮盘、7为右端拉杆、8为右端轴头。

图1 某大型转子三维模型剖视图

由图1可知，组成该型转子的零部件较多，所包含的几何特征更多。过多几何特征的存在，尤其是微小几何特征，不仅大幅增加计算量和时耗，而且会带来计算难以收敛的问题。按照以往计算经验，微小几何特征的去除几乎不会影响计算精度。因此，在进行整体网格划分之前，对组成转子的几个部件进行了特征去除工作，主要包括左端轴头、左端鼓桶、螺母、右端轴头、左端拉杆和右端拉杆等部件。图2a及b分别表示左端轴头特征去除前后的三维模型，这里将左端轴头端部凸台、顶锥孔、端面小孔以及气封槽等特征去除，其余部件特征去除与之类似，此处不再赘述。在去除微小几何特征之后，采用ABAQUS软件对各部件特征去除前后的离心应力进行了验算，结果两者应力集中分布几乎一致，计算精度和计算时间变化情况如表1所示。由表1可知，相比原模型，微小几何特征去除后各部件离心应力的计算精度下降很小，最大为1.23%，而计算耗时大幅降低，最大为46%，由此说明了特征去除的必要性。

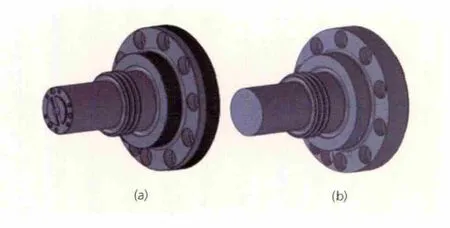
图2 左端轴头特征去除

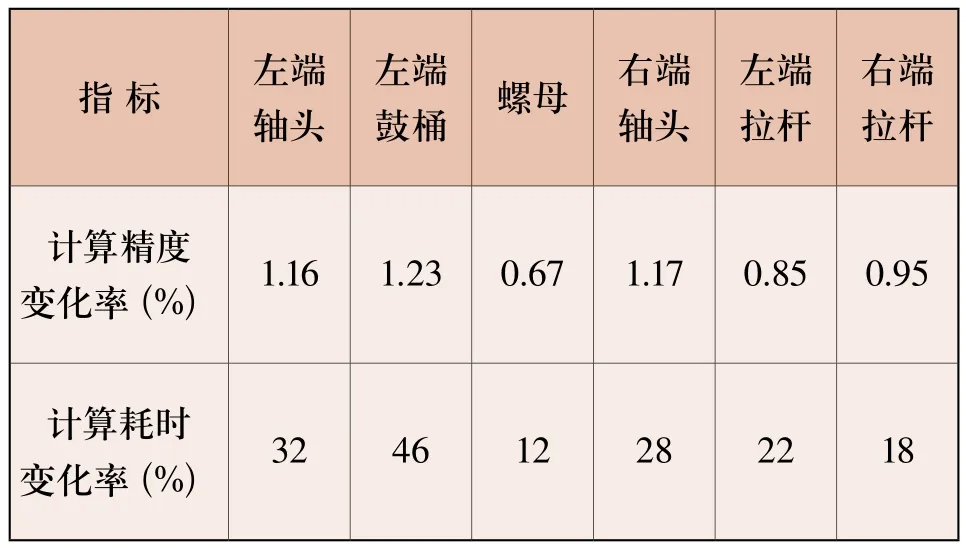
表1 特征去除前后计算效率变化情况

2 有限元建模分析

2.1 边界条件设置

将特征去除后的三维模型以*.step格式导入ABAQUS软件，赋予各部件相应的密度、杨氏模量和泊松比等材料属性；选取静态通用载荷步，设置好初始载荷步增量；分别在左右两轴承支承位置对应的转子轴段外圆面施加位移约束，左侧自由度全部约束，右侧除轴向平移自由度外，其余的自由度也全部约束。

旋转的转子产生离心作用，转子各部分质量在旋转过程中受到的离心作用力大小可由式1表示如下：

式中，m表示组成转子质量块的质量大小；ω表示转子旋转角速度；r表示质量块与旋转轴间的距离。由于该型转子实际工作转速为6 580r/min即689rad/s，因此可以预测转子旋转产生的离心作用将会导致较大的离心应力，这将很不利于转子的稳定运转。因此，有必要通过有限元法计算转子离心应力，以期改进转子结构，减小应力集中。本文在有限元分析软件ABAQUS中使用Rotational Body Force即旋转体力对转子离心作用加以模拟，通过指定转子绕x轴的角速度ω=689 rad/s，可将离心作用加载到模型中，如图3所示。

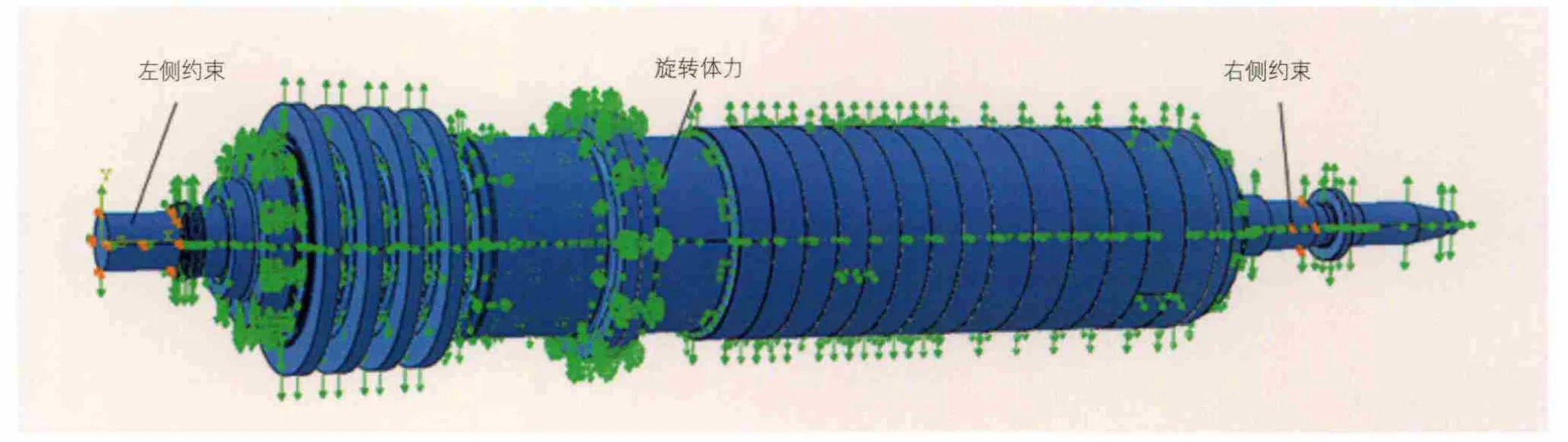
图3 转子边界条件设置

2.2 网格划分

在给定边界条件的情况下，离心作用产生的应力大小和分布主要取决于有限单元网格划分。网格划分过程中所选择的网格大小、疏密分布以及单元类型等都会对计算精度产生较大的影响，图4a为四节点四面体单元，其各节点多项式位移模式如式2所示。

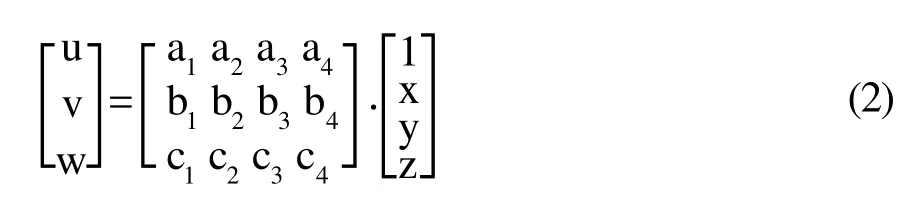
形函数如式3所示：

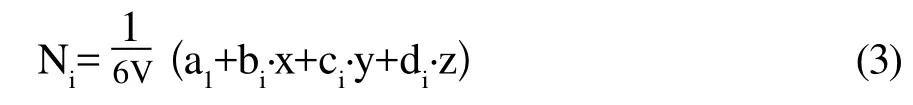
其中，V为体积单元，i=1，2，3，4。图4b为十节点四面体单元，节点多项式位移模式如式4所示：

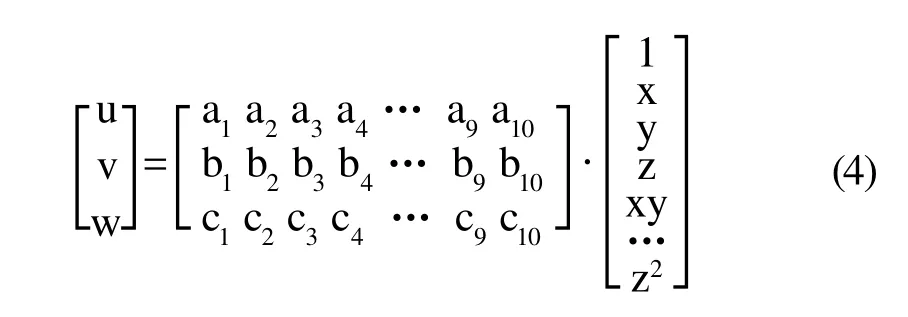
基于自然坐标系的形函数如式5～11所示：

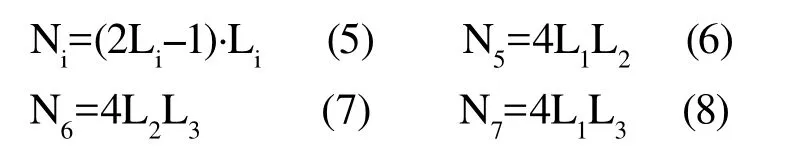
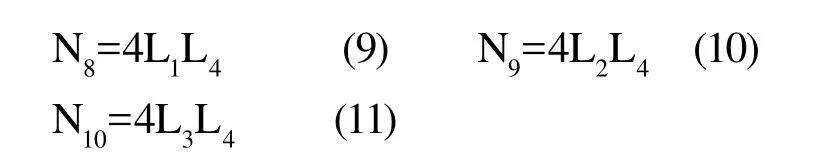
其中，i=1,2,3,4。由此可知，高次位移函数能更好地逼近复杂结构的位移分布，也即高阶单元能够更好地逼近实际结构中曲线和曲面，多项式位移插值函数阶数越高，计算精度也就越高。

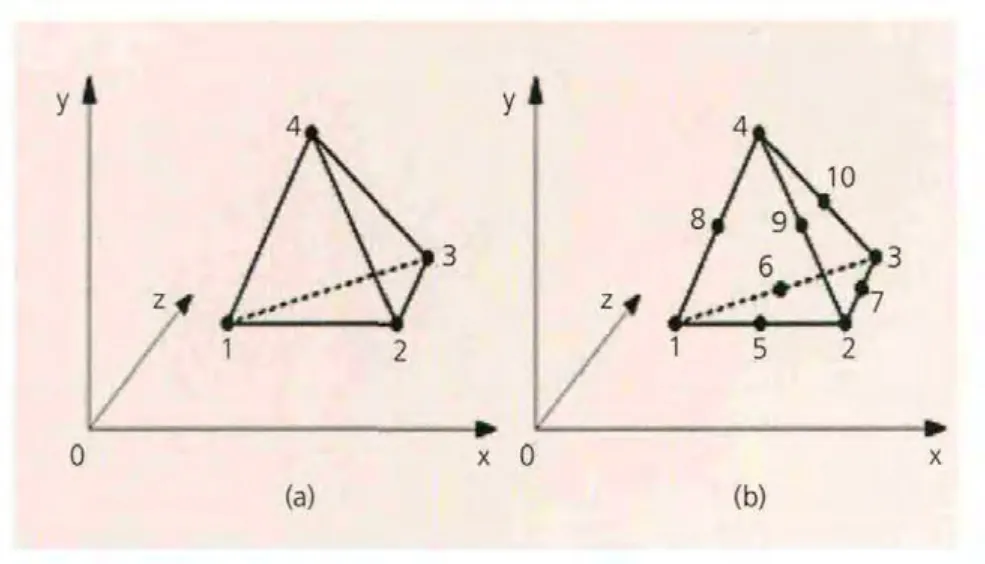
图4 四面体单元

本文采用如下方法来解决计算精度和计算耗时之间的矛盾：首先对整体转子进行四面体一阶单元网格划分，按照经验，确定1.5%为精度指标，以期用最小的计算资源确定合适的网格密度；然后再运用子模型法对所关心的部件进行二阶单元重新网格划分，获得更加精确的离心应力值。

分别用12号～21号大小的四面体单元种子对同一转子模型进行网格划分，得到了十组不同网格数目的有限元模型，以前后两者最大离心应力相差1.5%为界来选取相对合适的网格密度。当单元种子大小为13号时，计算得到转子各主要部件离心应力结果云图如图5～图7所示。

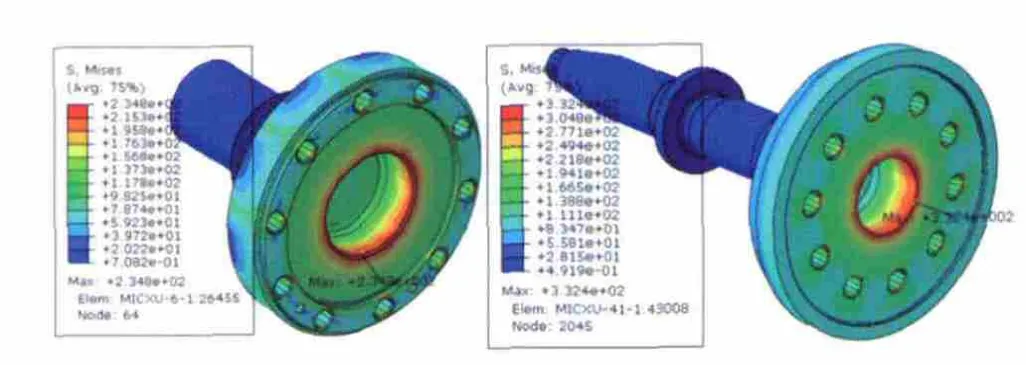
图5 左端/右端轴头离心应力分布

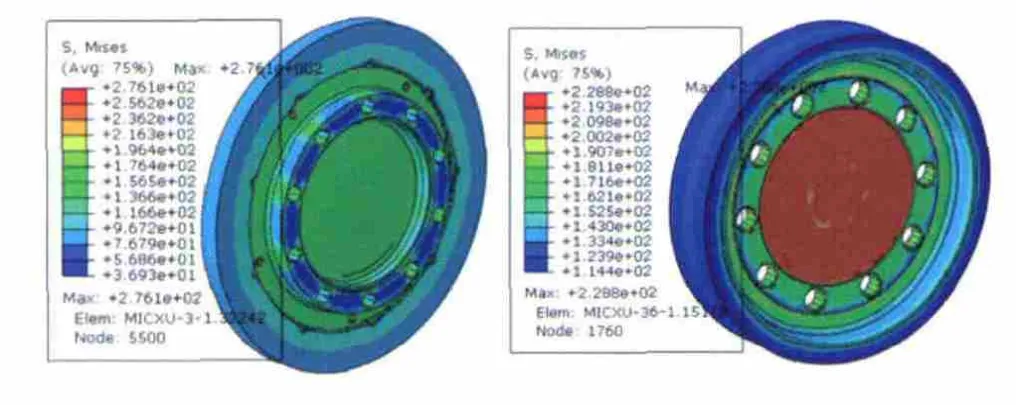
图6 左端/右端轮盘离心应力分布

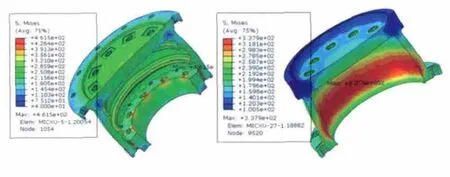
图7 左端/右鼓桶离心应力分布剖视图

2.3 结果分析

由图5～图7可知，两端轴头最大离心应力均出现在内腔边沿处；左端轮盘最大离心应力出现在冷却孔边沿；右端轮盘最大离心应力出现在中部最薄轮辐边缘；左端鼓桶最大离心应力出现在靠近左端一级轮盘的拉杆孔内沿；右端鼓桶最大离心应力则出现在中部外圆薄壁上。由此可以得到在该转子旋转过程中，对离心作用较敏感的位置如下：第一，含有腔体的部件，其腔体边沿处；第二，盘型部件的薄壁与厚壁接合处；第三，拉杆凸台与拉杆孔接触位置。这些结论可为该型转子的结构设计提供良好的参考。

通过10组不同网格数目的模型计算得到的转子各部件最大离心应力几乎分布在同一位置，其中最大应力值出现在左端鼓桶拉杆孔内沿，此处正是集腔体、薄壁和接触三大离心作用敏感因素于一体的位置，也进一步验证了前述离心应力分布规律结论的可信度。离心应力大小随网格数目变化规律如图8所示。由图8可以发现，当单元种子为13号即网格数目约为236万时，前后两者最大离心应力相差1.3%小于1.5%，已满足既定要求。由此可以认为整体转子网格划分已达最佳，无需再进行网格加密计算。

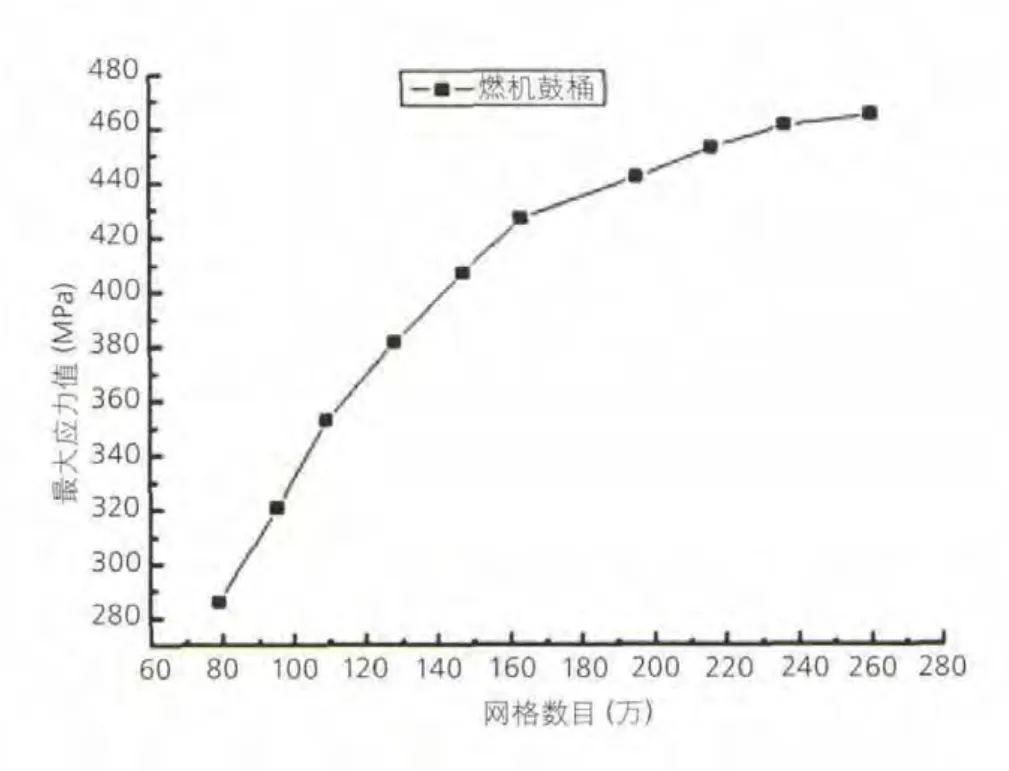
图8 最大离心应力随网格数目变化曲线

3 子模型法

通过前文的计算分析，得到了整体转子较合适的网格数目，可以认为整体网格数目这一因素不会对计算精度造成影响。但是由一阶四面体单元计算得到的应力值只能较好地反映该型转子整体的离心应力分布规律，其应力计算结果偏刚，往往比准确值略小，因此计算精度有待进一步修正。介于此，本文采用基于ABAQUS软件的子模型法，对其中应力最大的左端鼓桶作进一步的离心应力计算，采用种子号更小的二阶单元对其重新进行网格划分，以期利用较小的计算资源，得到更精确的计算结果。

在完成全局模型计算的基础上，去除了除左端鼓桶之外的其余转子组件，将左端鼓桶的两端面及拉杆孔内表面一起定义为子模型边界，计算过程中读入全局模型结果文件作为其边界条件和驱动变量。图9为沿轴向依次选取的左端鼓桶轴截面上的21个节点，分别在全局模型和子模型中计算得到的离心应力值。

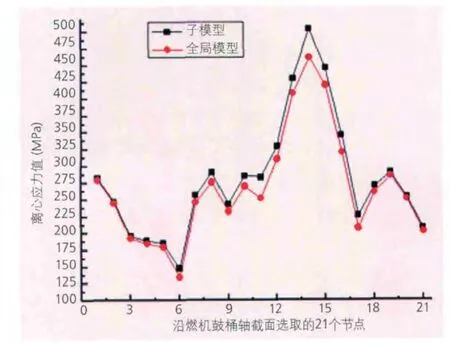
图9 两种模型下左端鼓桶节点离心应力值

由图9可以发现，子模型法计算得到的左端鼓桶各节点离心应力分布规律基本与全局模型类似，并且离心应力值比全局模型中略高；全局模型中左端鼓桶最大应力为461MPa，小于子模型中的504MPa；最大应力都发在14号节点即鼓桶靠近左端第一级轮盘的拉杆孔内沿。由于在子模型中运用了节点数更多的二阶单元，并且单元种子号更小，因此有理由认为离心应力计算值更加精确。子模型与全局模型的离心应力有限元分析效率如表2所示，由此可以看出子模型法不仅计算精度颇高，而且计算耗时可大幅减少。该型转子其余部件子模型法计算过程与此类似，此处不再赘述。

表2 子模型与全局模型计算效率比较

4 结 论

为解决大型复杂结构精确、高效的有限元计算问题，本文以某大型旋转机械转子离心应力有限元分析为例，采用全局模型确定网格密度、子模型计算最终结果的方法，得到主要结论如下：

(1)对整个转子而言，离心应力最大位置在转子中部鼓桶上；对各组成部件而言，应力集中主要发生在含腔体、薄壁和接触等因素的位置；

(2)为确定大型复杂三维模型合适的有限元网格密度，可以通过某一精度指标，以较粗略的有限单元进行多次网格划分，从而得到满足指标的最经济的网格数目；

(3)相比全局模型，子模型法计算易收敛，效率高，精度好，非常适合旋转机械转子等大型结构的有限元计算。

[1]刘恒，陈丽.周向均布拉杆柔性组合转子轴承系统的非线性动力特性[J].机械工程学报 2010，46（19）：53-62.

[2]何鹏.分布式拉杆转子动力学特性分析[D].哈尔滨：哈尔滨工业大学，2009.

[3]杜世渊，阎淑丽.高速转子离心力及其效应的仿真与分析[J].机械管理开发，2010, 25(6)：201-202.

[4]王俊瑜，纪冬梅，姚秀平，等.汽轮机启动过程中转子应力的主要影响因素[J].上海电力学院学报，2012,28(3)：238-246.

[5]Hamdi T，Mehmet P.Evaluation of gas turbine rotor dynamic analysis using finite element method[J].Measurement, 2012，45(5)：1089-1097.

[6]Blacker T.Automated conformal hexahedral meshing constraints，challenges and opportunities[J].Engineering with computers，2001,17(3)：201-210.

[7]李浦，袁奇，高进，等.周向拉杆转子轮盘端面齿接触应力分析[J].热力透平，2013, 42(1)：25-29.

[8]Tomislav S，Anica T, Kristian L.Parametric study of operating and geometry characteristics effect on heat transfer in annular finned tube heat exchanger[J].Eng.Rev，2009，29(1)：25-36.

[9]高素荷，姚河省.网格划分密度和有限元求解精度研究[C]/第三届中国CAE工程分析技术年会论文集.大连，2007：480-485.

[10]石亦平，周玉蓉.ABAQUS有限元分析实例讲解[M].北京：机械工业出版社，2006：60-61.