Lauwerier映射的混沌控制

郭 峰， 谢建华， 乐 源

(西南交通大学力学与工程学院，四川成都 610031)

由于混沌现象的广泛存在，最近几十年，在非线性控制领域内，混沌控制的研究受到越来越多的关注.人们通过对各种混沌现象产生机理的研究，在不断发现新的混沌奇异性的同时，也逐渐认识到混沌运动对系统的危害，甚至会给系统带来灾难性的后果.而混沌在某些环境下是有用的，因此，在某些实际系统中，控制混沌或者混沌的反控制是非常重要和有现实意义的.

混动控制的研究始于20世纪80年代末，早期的研究思路是用现有的动力学控制策略破坏混沌运动发生的条件.文献[1]提出控制混沌的OGY方法.文献[2-9]根据各种不同情况提出了不同的改进措施，进一步发展了OGY方法.混沌吸引子中的高周期态控制以及高维动力学系统的混沌控制是OGY方法发展的一个重要方向.文献[10]采用线性系统控制中的极点配置技术，对OGY方法进行了改进.

文献[11]对两维的Lauwerier映射进行了研究，当参数满足0＜b＜0.5、a==4时，系统出现混沌现象.文献[12]对Lauwerier吸引子的结构及其动力学行为进行了分析.文献[13]研究了Lauwerier映射混沌吸引子的遍历性，但目前尚未见Lauwerier映射的混沌控制问题研究，对该系统的混沌控制有助于解决对高周期态和高维系统的控制问题.

本文采用极点配置法，对Lauwerier映射出现的混沌运动进行控制，在保持原系统不改变的情况下，将不稳定的周期-1轨道和周期-2轨道控制在稳定的周期轨道上，对不同调节器极点对混沌控制时间的影响进行了分析.

1 极点配置方法

考虑如下映射:

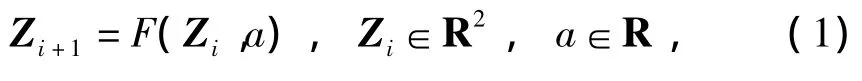
式中:

F是充分光滑的函数;

a是可控的实参数，在某时间段内要求

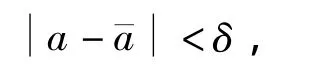
δ为控制区域.

若Z*()为映射式(1)的不稳定周期-1轨道，则该映射可近似线性化为

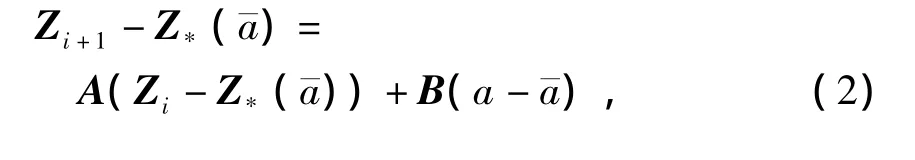
式中:

A=∂F/∂Z和B=∂F/∂a在Z=Z*()和a=处求值.

假设依赖时间的控制参数a是关于变量zi的线性函数，即

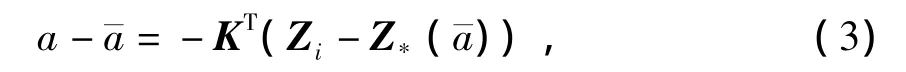
式中:

KT为反馈增益矩阵.

将式(3)代入式(2)得到

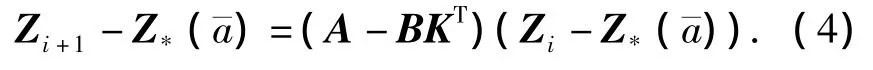
由式(4)知，若矩阵A－BKT是渐进稳定(即其特征值的模均小于1)的，则不动点Z*(¯)将变为稳定的.

关键问题是确定满足上述条件的矩阵KT，文献[14]给出了求解极点配置的方法，极点配置问题存在唯一解的充要条件是矩阵Cn×n是秩为n的可控矩阵.

式中:

βi(i=1，2，…，n)为矩阵 A 的特征多项式

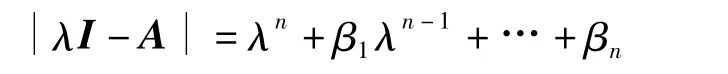
的系数;

α1，α2，…，αn是 A －BKT的特征多项式

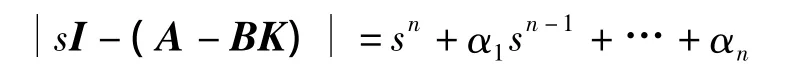
的系数.

极点配置问题的解由

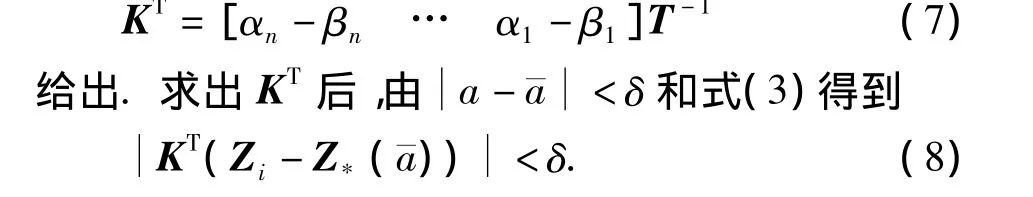
2 平面Lauwerier映射的混沌控制

考虑定义在区域 Q=[0，1]×[0，1]上的两维Lauwerier映射

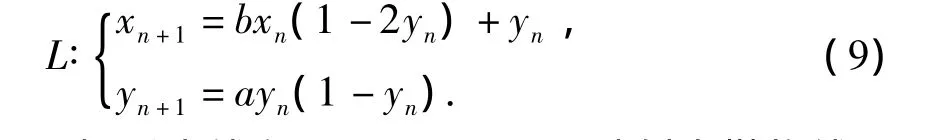
式(9)把垂直线段x=ξ(0≤y≤1)映射为抛物线.

图1中，把水平线段y=η(0≤x≤1)映射为水平线段y=4η(1－ η)(η≤x≤η +b(1 －2η))，因而式(9)把Q映射到其内部，形成一个类似Smale马蹄形状的像L(Q).

图1 正方形Q及其像L(Q)Fig.1 Square Q and L(Q)

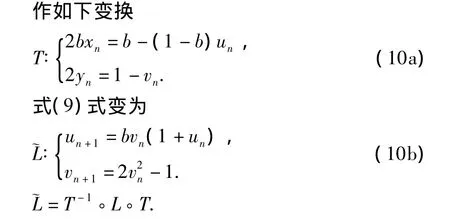
对式(10b)进行迭代，再取极限得到

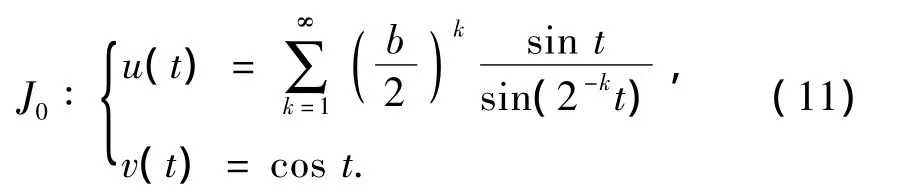
再由式(10a)的变换，将式(11)代入式(10a)，可以得到式(9)的不变曲线J的表达式为

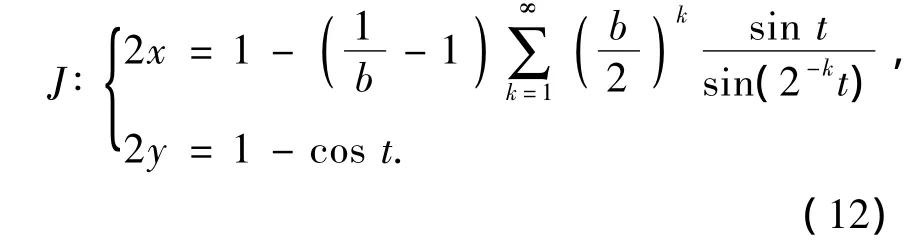
由吸引子的定义和文献[12]的分析，可知对Q内任一点x，当n→∞时Fn(x)→J－，不变曲线J的闭包构成了式(9)的吸引子.

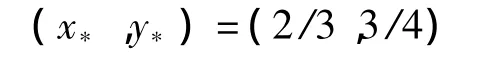
和周期-2轨道:

当式(9)中a=3时出现周期倍化分岔，在a=3.6时出现混沌运动，图2为式(9)的混沌相图，圆点是其周期-1轨道，加号表示周期-2轨道.

图2 Lauwerier映射的混沌相图Fig.2 Chaotic phase diagram of Lauwerier mapping

2.1 控制在周期-1轨道

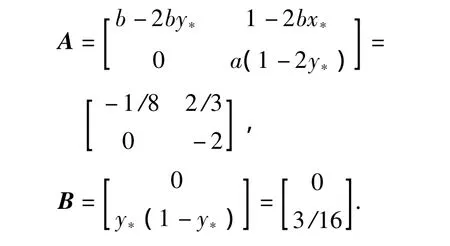
可控矩阵是秩为2的矩阵βi(i=1，2)为矩阵A的特征多项式系数，

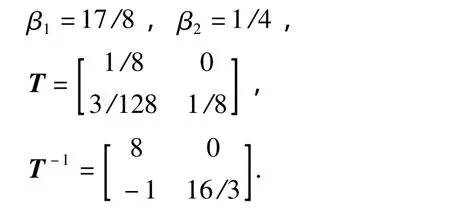
求得A的特征多项式的根为λs=－1/8，λu=－2，α1和α2是A－BKT的特征多项式的系数，若假设A－BKT的特征根μ1和μ2为调节器极点，即

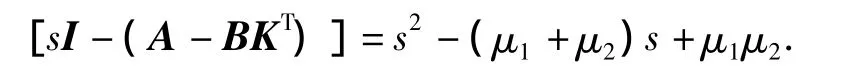
得到根与系数的关系为

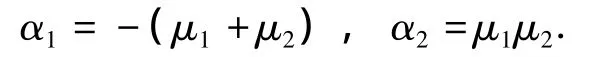
当 μ1=1时，α1= －1－α2;当 μ1= －1时，α1=1+α2;当 μ1μ2=1时，α2=1.因此，α1和 α2的取值范围如图3中的灰色区域所示.

在图3中三角形区域内，对α1和α2取不同的值使得控制时间不同.由第1节可知KT的取法不是唯一的，只要在三角形区域中取α1和α2值，然后求得矩阵KT，都能满足矩阵A－BKT是渐进稳定的，所以取 μ1=0，μ2=λs，即(α1，α2)=(－ λs，0)时得

式中:u为阶跃函数，

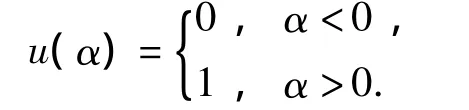
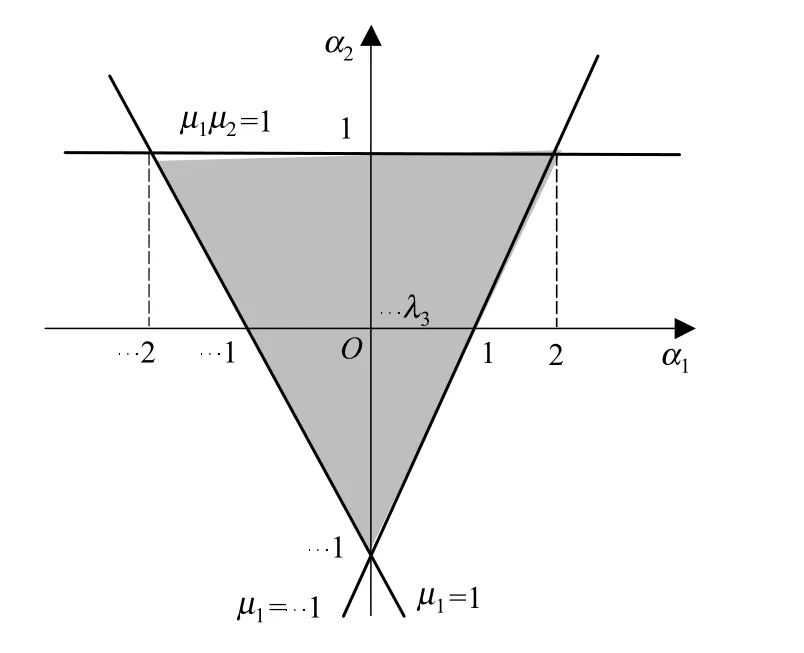
图3 调节器极点的选取区域Fig.3 Selection of regulator pole area

图4表示取不同的α1和α2时将混沌控制在周期-1 轨道，控制区域 δ=0.02.当

α1=1/8， α2=0

时，系统经过230多次的迭代实现控制的目的.当α1=1/6， α2= －1/4

时，经过3 300次的迭代完成混沌控制.

2.2 控制在周期-2轨道

最直接的方法就是将式(9)进行迭代，则周期轨道上的点都是不动点，然后由上述方法进行控制.当=4时，得到周期-2轨道为

(x1，y1)=(0.409 0，0.904 5)，

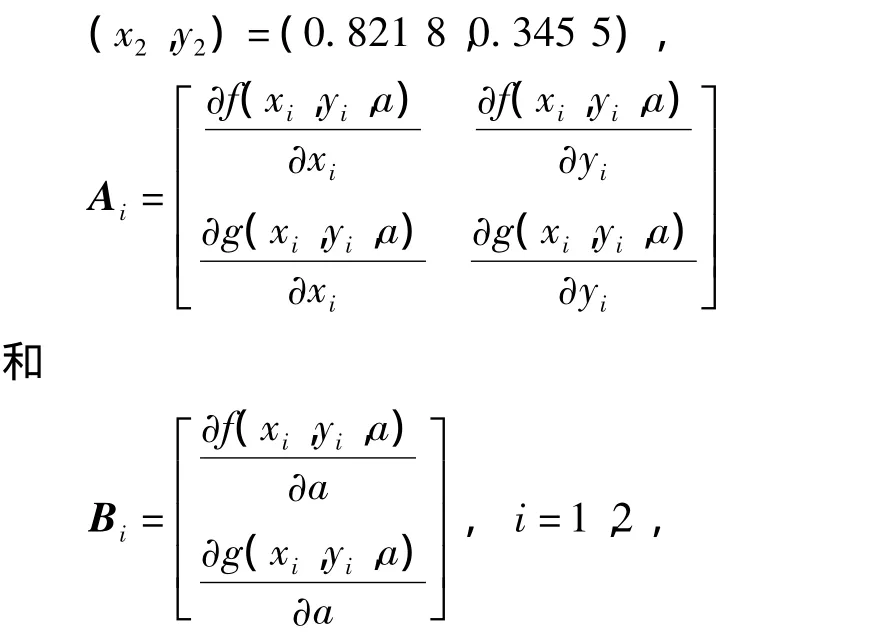
式中:f和g为通过式(9)的二次迭代所得的函数.

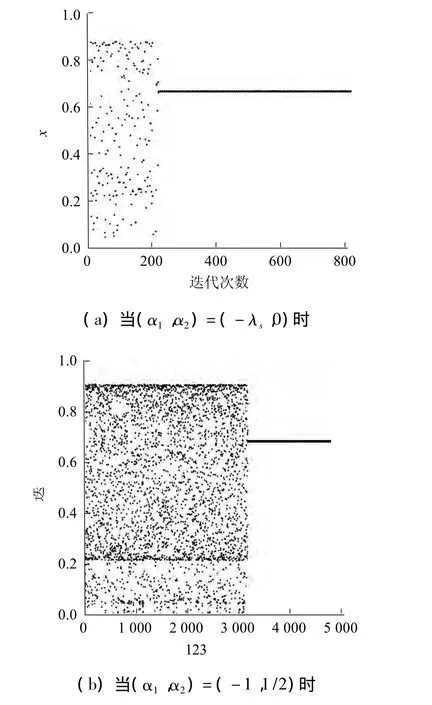
图4 将混沌运动控制在周期-1轨道上Fig.4 Control chaos to period-1 orbit

计算可控矩阵

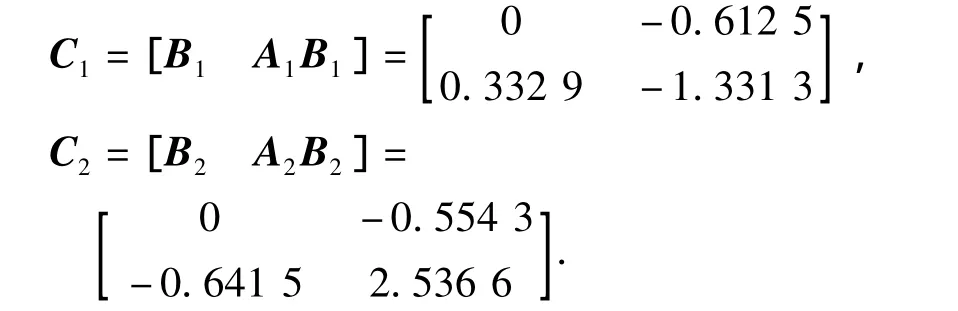
β1i(i=1，2)为矩阵A1的特征多项式的系数，β11=1.850 0，β12=0.579 9，特征根为 λ1s=－0.399 9，λ1u= －1.450 1，α11和 α12是 A1－B1KT1的特征多项式的系数，取于是得反馈增益矩阵

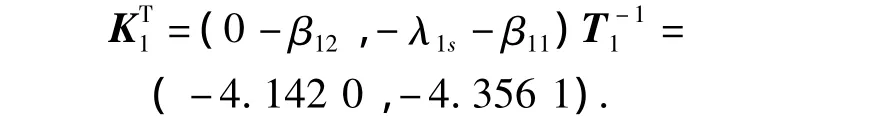
β2i(i=1，2)为矩阵A2的特征多项式系数，

β21=3.926 5， β22=－0.109 0，特征根为 λ2s=0.027 6，λ2u= － 3.954 1.取(α21，α22)=(－ λ2s，0)，得到

得到反馈增益矩阵 KT2=(－0.394 7，6.164 0).

控制率可由下式给出

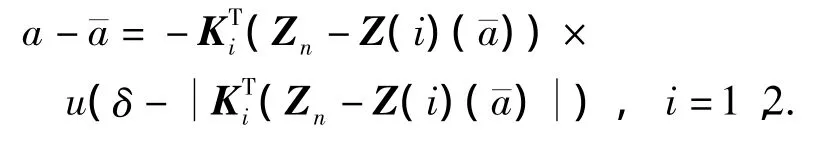
如图5 所示，取 δ=0.02、α11= － λ1s、α12=0、α21=－λ2s和α22=0经过430次的迭代将混沌运动控制在周期-2轨道上.

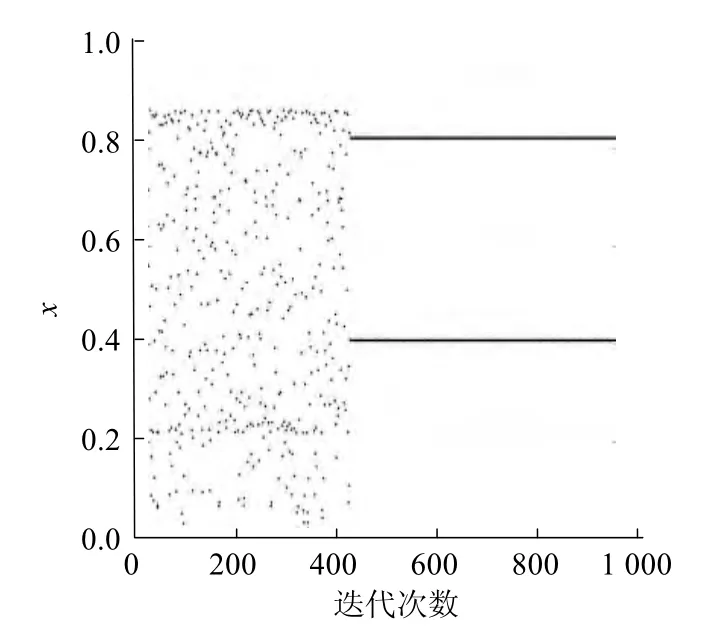
图5 将混沌控运动制在周期-2轨道上Fig.5 Control chaos to period-2 orbit

3 结束语

运用改进的OGY方法，在不改变原系统的基础上，实现了对Lauwerier映射的混沌进行控制.利用线性控制理论中的极点配置方法，选择控制参数的扰动量，分别将不稳定的周期-1轨道和周期-2轨道控制在稳定的周期-1轨道和周期-2轨道上，结果显示，选取不同的极点值时，控制时间会不同.参考文献:

[1]OTT E， GREBOGI C， YORKE J A. Controlling chaos[J].Phys.Rev.Lett.，1990，64(11):1196-1199.

[2]PYRAGAS K.Continuous control of chaos by selfcontrolling feedback[J]. Phys. Lett. A， 1992，170(6):421-428.

[3]SHINBROT T，GREBOGI C，OTT E，et al.Using small perturbations to control chaos[J].Nature，1993，363:411-417.

[4]PYRAGAS K.Predictable chaos in slightly perturbed unpredictable chaotic systems[J]. Phys. Lett. A，1993，181(3):203-210.

[5]AUERBACHD， GREBOGIC， OTTE， etal.Controlling chaos in high-dimensionalsystems[J].Phys.Rev.Lett.，1992，69(24):3479-3482.

[6]BOCCALETTI S，GREBOGI C，LAI Y C，et al.The control of chaos:theory and applications[J].Phys.Rep.，2000，329:103-197.

[7]YAGASAKI K， UOZUMI T. A new approach for controlling chaotic dynamical systems[J].Phys.Lett.A，1998，238:349-357.

[8]YAGASAKI K，UOZUMI T.Controlling chaos using nonlinear approximations and delay coordinate embedding[J].Phys.Lett.A，1998，247:129-139.

[9]YAGASAKI K.Extension of a chaos control method to unstable trajectories on infinite-or finite-time intervals:experimental verification[J].Phys.Lett.A，2007，368:222-226.

[10]FLIPE R J，GREBOGI C，OTT E.Controlling chaotic dynamical systems[J].Phys.D，1992，58:165-192.

[11]LAUWERIER H A. Thestructureofastrange attractor[J].Phys.D，1986，21(1):146-154.

[12]刘曾荣，秦文新，谢惠民.Lauwerier吸引子的结构和动力学行为[J].科学通报，1992，37(14):1269-1278.LIU Zengrong， QINWenxin， XIEHuimin. The structure and dynamic ofLauwerierattractor[J].Chinese Science Bulletin，1992，37(14):1269-1278.

[13]曹永罗.Lauwerier奇怪吸引子的遍历性及其结构[J].数学学报，1999，42(6):965-968.

CAO Yongluo.The ergodicity and the structure of Lauwerier strange attractor[J]. Journal of Mathematics，1999，42(6):965-968.

[14]OGATA K.Controlling engineering[M].2nd Ed.Englewood Cliffs:Prentice Hall，1990:782-784.