一类混合时滞复值神经网络的动态行为分析
徐晓惠, 张继业, 赵 玲
(1. 西华大学交通与汽车工程学院,四川 成都610039;2. 西南交通大学牵引动力国家重点实验室,四川 成都610031)
众所周知,神经网络在信号处理、模式识别、联想记忆等领域取得了广泛的应用[1-2]. 神经网络平衡点的存在性与稳定性是其应用的前提条件,因此学者们对不同类型的神经网络平衡点的动力学行为进行了深入研究,并取得了很多重要的研究成果[3-10].文献[1-10]的研究成果都是针对实值神经网络进行展开的. 然而,实值神经网络在一些领域里应用时具有一定的局限性. 例如在交通系统中,当采用复值神经网络取代实值神经网络进行路牌识别后,由于复值信号携带的信息较实值信号更加丰富,可明显减少错误,提高路牌识别的准确度[11].鉴于复值神经网络应用越来越广泛,并且具有比实值神经网络更加复杂的性质,因此对复值神经网络平衡点的动力学行为研究是非常必要的.文献[12]研究了一类离散复值神经网络,并给出了判定平衡点存在性、唯一性和指数稳定的判定定理.文献[13]在假设复值激活函数关于神经元状态分别满足有界或Lipschitz 条件的情况下,利用LMI 方法研究了一类具有固定时滞的复值神经网络平衡点的动态行为. 此外文献[14-16]也对复值神经网络的动态行为进行了深入研究.
综上分析,虽然关于复值神经网络动态行为的研究已经取得了一些成果,然而所研究的复值神经网络模型都较为简单.在实际应用时,一方面,在网络的硬件实现中,由于信号传输速度的有限性,使网络系统中时间滞后不可避免.在神经网络中引入时间滞后参量,有利于移动目标的图像处理、移动物体速度的确定和模式分类. 另一方面,一般情况下,在神经元较少的时滞神经网络中,有限时滞是一种较好的近似模型. 然而,由于网络中各种并行通道的存在,使网络具有一定的空间特征,这使得学者们试图通过分布时滞来模拟网络的时滞.目前关于复值神经网络动态行为的研究尚未在模型中考虑混合时滞的情形. 因此,本文将在一类复值神经网络模型中同时考虑可变时滞和分布时滞,利用矢量Lyapunov 函数法和M 矩阵理论,研究其平衡点的存在性、唯一性以及指数稳定性.
1 模型描述、基本假设以及引理

考虑如下混合时滞复值神经网络:



式中:μkj(β)是[0,δ)上的连续函数,且μkj(0)=1,这里δ >0.
假设系统(1)的初始条件是zk(s)=φk(s),其中φi(s)为(-∞,0]上的有界连续函数.
记z#=(,…)T为系统(1)的平衡点.
定义1 若存在常数Γ >0 和λ >0,对于所有J∈Cn及t≥0,有
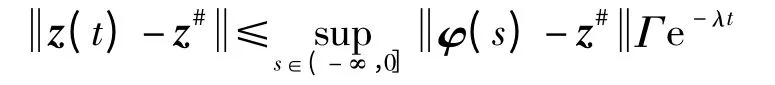
成立,则称系统(1)的平衡点z#是指数稳定的.

令L=diag(l1,l2,…,ln).
引理1[2]对于矩阵A =(akj)n×n∈Rn×n,如果所有非对角元素akj≤0,k≠j,则下面陈述是等价成立的:
(1)A 是M 矩阵;
(2)A 的各阶顺序主子式均为正;
(3)存在u∈Rn>0,使得Au >0;
(4)A 的所有特征根的实部为正.

定义H(z)=[H1(z),H2(z),…,Hn(z)]T是与系统(1)相关的一个映射,其中

若H(z)是Cn上的同胚映射,那么显然系统(1)具有唯一平衡点z#.
2 主要结论
定理1 若假设1 是成立的,且矩阵W =(wkj)n×n是M 矩阵,那么对于任意输入J∈Cn,系统(1)存在唯一平衡点z#,其中

证明 由于矩阵W=(wkj)n×n是M 矩阵,根据引理1 可知,存在正向量ξ=(ξ1,ξ2,…,ξn)T,使得

那么存在一个充分小的正数使得不等式(4)成立:

下面将证明映射H(z)是一个同胚映射.
(1)首先证明Hk(z)是单叶映射.
若存在u,v ∈Cn,且u ≠v,使得Hk(u)=Hk(v),即

将式(5)两边同时乘以(uk-vk)*,整理有
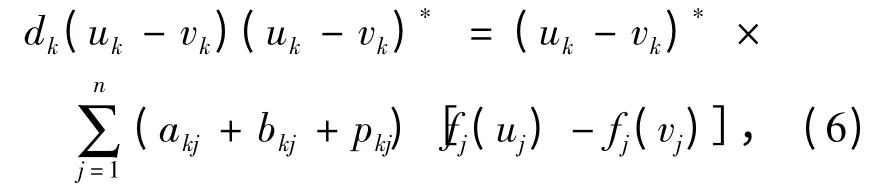
将式(6)两边同时取模,并考虑到假设条件1,有

将式(7)进一步整理,有

其中

即

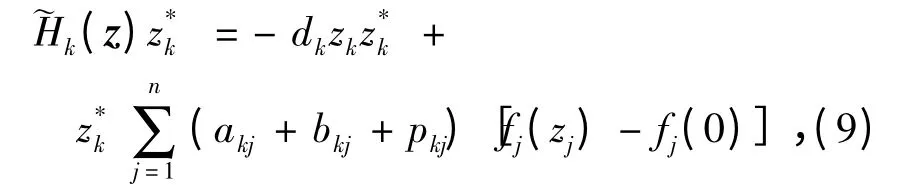
将式(9)两边同时取共轭,有

进一步,将式(9)和式(10)相加,并考虑到假设1,有

将式(11)两边同时乘以ξk,k =1,2,…,n,并求和得到
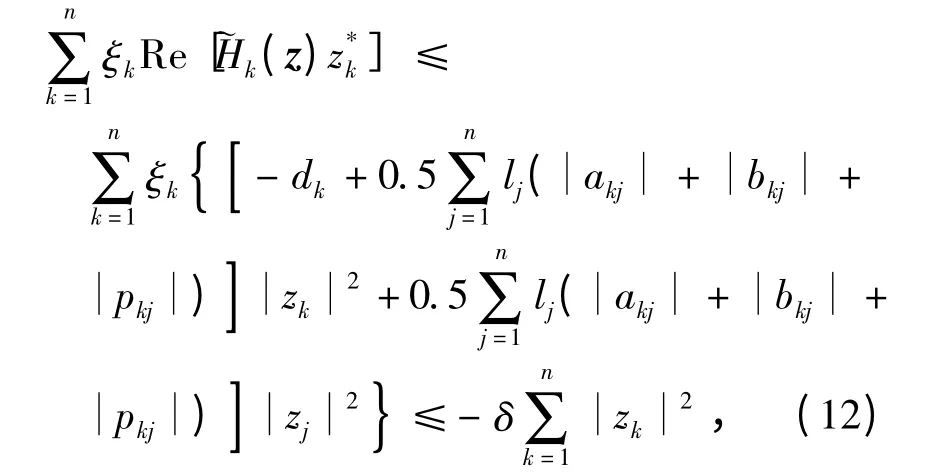
利用Holder 不等式,进一步整理式(12),有


综合(1)、(2)可知映射H(z)是Cn上的一个同胚映射,因此系统(1)存在唯一平衡点.
接下来将给出判定系统(1)的平衡点z#指数稳定的充分条件.
定理2 若假设1 是成立的,且矩阵W =(wkj)n×n是M 矩阵,那么任意外部常输入J∈Cn,系统(1)的平衡点z#是指数稳定的.
证明 令~z=z-z#,则系统(1)可改写为

式中:gj(~zj)=fj(zj)-fj().
方程(14)的初始条件为ψk(s)=φk(s)-,-∞<s≤0.由定理2 条件可知系统(1)的平衡点z#存在且唯一,故方程(14)存在唯一平衡点~z=0.
构造函数:

根据式(3)可知:

由于Fk(β)是关于β 的连续函数,必然存在常数λ >0,使得Fk(λ)<0,即

选择如下向量Lyapunov 函数:

在不引起混淆的情况下,将Vk(~zk(t),t)记作Vk(t),k=1,2,…,n.
计算Vk(t)沿方程(14)的导数,并考虑到假设1,有

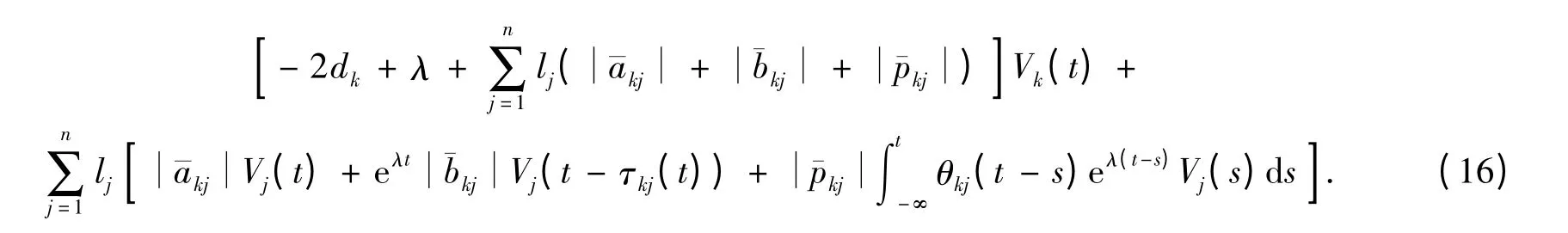
定义曲线ζ={η(χ)∶ηk=ξkχ,χ >0,k =1,2,…,n}和集合Ω(η)={h∶0≤h≤η,η∈ζ}.显然当χ >χ',Ω(η(χ))⊃Ω(η(χ')).
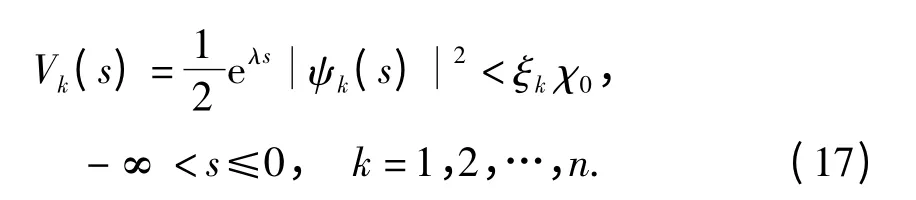


根据定义1 知,系统(14)的零解~z =0 是指数稳定的,也就是说系统(1)的平衡点~z#=0 是指数稳定的.
当系统(1)中矩阵P =0 时,该系统仅含有可变时滞,即

当系统(1)中矩阵B =0 时,该系统仅含有无穷时滞,即

系统(19)和(20)中的符号定义与系统(1)是相同的.进而,由定理1 和定理2 很容易得到如下推论:
推论1 若假设1 是成立的,且矩阵W =(wkj)n×n是M 矩阵,那么对于任意输入J∈Cn,系统(19)存在唯一指数稳定的平衡点z#,其中

推论2 若假设1 是成立的,且矩阵W =(wkj)n×n是M 矩阵,那么对于任意输入J∈Cn,系统(20)存在唯一指数稳定的平衡点z#,其中

注1 当系统(19)中可变时滞τkj为固定常数τj(j=1,2,…,n)时,文献[13]采用LMI 方法对此类复值神经网络的动态行为进行了研究,并得到了相应的稳定性判定条件,见定理4[13]. 由于基于LMI 方法(本质上属于加权Lyapunov 函数法)所得到的稳定性判据含有待定矩阵,即文献[13]中的判据是隐式的,因此不便于应用. 本文所得到的判据是基于向量Lyapunov 函数法所得到的显式判据,不但形式简单且应用方便.
注2 当系统(1)中的神经元状态定义在实数域时,模型(1)与文献[2]所研究的实值神经网络模型相同,故本文所研究的模型更具有一般性. 此时,本文的研究方法和所建立的判据对相应的实值神经网络仍然适用.
3 算 例
考虑如下复值神经网络:
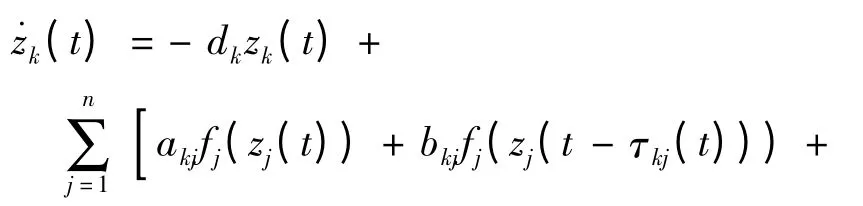

其中:z1(t)=x1(t)+y1(t)i,
z2(t)=x2(t)+y2(t)i.
假设自反馈矩阵

加权矩阵分别为

激活函数为

外部输入J1=J2=0.
经计算,有
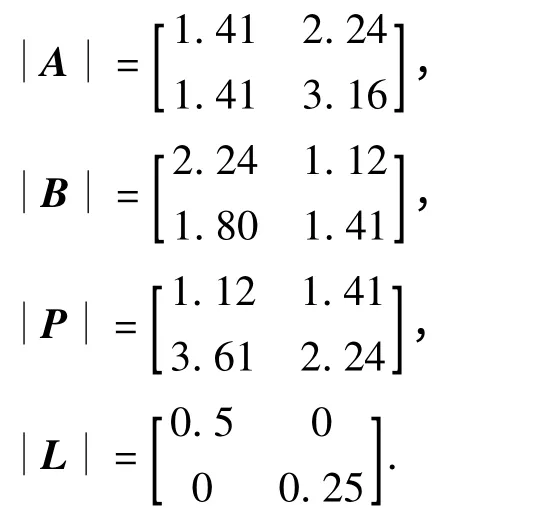
进一步计算,有

由引理1 可知矩阵W 是M 矩阵. 根据定理1和定理2 可以得出结论:系统(21)存在唯一平衡点,且该平衡点是指数稳定的.
令系统(21)中的可变时延为

令
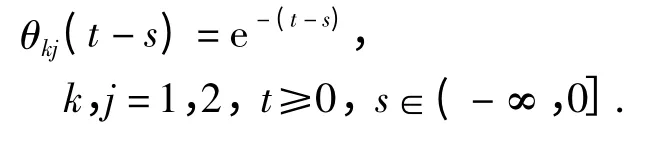
令初始条件为

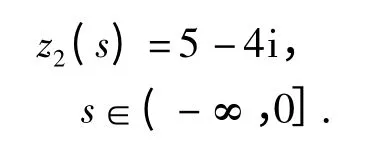
图1 给出了系统(21)的神经元实部状态曲线和虚部状态曲线,图2 给出了该系统的神经元状态幅值曲线.由仿真结果可以看出系统(21)的平衡点是唯一存在且稳定的.

图1 神经元状态曲线Fig.1 The state curves of neuro of Eq. (21)

图2 神经元状态幅值曲线Fig.2 The amplitude curves of neuro states of Eq. (21)
4 结束语
本文研究了一类具有可变时滞和无穷时滞的复值神经网络的动态行为. 假设神经元状态、加权矩阵以及激活函数定义在复数空间.首先利用同胚映射相关引理以及M 矩阵理论,分析了系统平衡点的存在性和唯一性. 然后利用向量Lyapunov 函数法,研究了该系统平衡点指数稳定性,并得到了判定该系统存在性、唯一性和指数稳定性的充分条件.最后通过一个数值仿真算例验证了所得到结论的正确性.
致谢:西华大学重点科研基金项目(No.zl320312);汽车工程四川省高等学校重点实验室开放研究基金资助项目(szjj2013-030).
[1] LAMPINEN J,VEHTATI A. Bayesian approach for neural networks:review and case studies[J]. Neural Networks,2001,14(3):257-274.
[2] ZHANG Jiye, SUDA Y, IWASA T. Absolutely exponential stability of a class of neural networks with unbounded delays[J]. Neural Networks, 2004,17(3):391-397.
[3] 龙兰,徐晓惠,张继业. 时滞Cohen-Grossberg 神经网络的全局稳定性[J]. 西南交通大学学报,2008,43(3):381-386.LONG Lan,XU Xiaohui,ZHANG Jiye. Global stability analysis in Cohen-Grossberg neural networks with unbounded time delays[J]. Journal of Southwest Jiaotong University,2008,43(3):381-386.
[4] SHAO Jinliang,HUANG Tingzhu,ZHOU Sheng. Some improved criteria for global robust exponential stability of neural networks with time-varying delays[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(12):3782-3794.
[5] ZHANG Huaguang,WANG Zhanshan,LIU Derong.Global asymptotic stability of recurrent neural networks with multiple time-varying delays[J]. IEEE Transactions on Neural Networks,2008,19(5):855-873.
[6] LIN Da,WANG Xingyuan. Self-organizing adaptive fuzzy neural control for the synchronization of uncertain chaotic systems with random-varying parameters[J].Neurocomputing,2011,74(12/13):2241-2249.
[7] HUANG Yujiao, ZHANG Huaguang, WANG Zhanshan. Dynamical stability analysis of multiple equilibrium points in time-varying delayed recurrent neural networks with discontinuous activation functions[J]. Neurocomputing,2012,91(1):21-28.
[8] BAO Gang, ZENG Zhigang. Analysis and design of associative memories based on recurrent neural network with discontinuous activation functions[J].Neurocomputing,2012,77(1):101-107.
[9] ZHU Song,LOU Weiwei,SHEN Yi. Robustness analysis for connection weight matrices of global exponential stability of stochastic recurrent neural networks[J]. Neural Networks,2013,38(1):17-22.
[10] ENSARI T,ARIK S. New results for robust stability of dynamical neural networks with discrete time delays[J]. Expert Systems with Applications,2010,37(8):5925-5930.
[11] 杨杰,王直杰,董宗祥. 复数Hopfield 神经网络在路牌识别中的应用[J]. 微计算机信息,2010,26(8):161-163.YANG Jie,WANG Zhijie,DONG Zongxiang. Road sign recognition using complex-valued Hopfield neural network[J]. Microcomputer Information, 2010,26(8):161-163.
[12] SREE H R V,MURTHY G R. Global dynamics of a class of complex valued neural networks[J].International Journal Neural Systems,2008,18(2):165-171.
[13] HU Jin,WANG Jun. Global stability of complexvalued recurrent neural networks with time-delays[J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(6):853-864.
[14] LEE D Q. Relaxation of the stability condition of the complex-valued neural networks[J]. IEEE Transaction on Neural Networks,2001,12(5):1260-1262.
[15] LIU Xiaoyu,FANG Kangling,LIU Bin. A synthesis method based on stability analysis for complex-valued Hopfield neural network[C]∥Proceedings of the 7th Asian Control Conference. Hong Kong:[s. n.],2009:1245-1250.
[16] DUAN Chengjun,SONG Qiankun. Boundedness and stability for discrete-time delayed neural network with complex-valued linear threshold neurons[J]. Discrete Dynamics in Nature and Society,2010:368379-1-368379-19.

