“平面支架”实验验证支架力学行为公式

杨 杰， 杨 基， 徐 江， 刘宇杰， 黄 楠

(1.西南交通大学力学与工程学院，四川 成都 610031;2.西南交通大学材料工程与科学学院，四川 成都 610031)

当前采用支架介入术治疗各种心血管疾病已经非常普遍，这是治疗血管狭窄的首选手术方法.对支架的力学性质的研究能够帮助解决临床支架植入过程中以及长期使用中遇到的问题.血管支架力学性质的研究一般通过有限元法和实验方法.文献[1-5]的研究表明支架的力学性能和施加的压力有关.支架撑开过程经历了弹性阶段和塑性阶段.文献[6-7]采用有限元法研究了支架的参数对于支架自身支撑性能的影响，文献[8-9]通过实验研究了支架的力学性质，包括径向弹性回弹、柔顺性、压力-直径关系等.但是这些研究都没有对血管支架撑开的弹性阶段和塑性阶段的力学性质进行深入的理论分析.

文献[10-11]通过对血管支架力学行为的理论分析，提出了弹性径向刚度公式和塑性极限压力公式，该公式首次得到了血管支架设计的各种参数与其撑开和支撑过程中力学性能的定量化关系，并使用有限元法进行了初步的验证，但该公式未经过实验验证.实验验证该公式具有较大的难度，其原因是，作用在支架上的载荷必须用球囊加载，需要剔除球囊影响.

本文中提出了“平面支架单元”的概念.在考虑等效的原则下，将支架单元“展开”为一个平面，并做几何“放大”，在实验上实现剔除球囊影响.

1 公式描述

管状支架一般由多个相同的主筋环段和连接筋构成.连接筋部分用以保持支架的完整性和柔顺性，主筋环段提供支撑力，使支架拥有撑开堵塞血管的能力.根据主筋环段的对称性(如图1)，文献[10-11]中取最基本的对称单元，研究了血管支架的力学性质，并提出了支架弹性径向刚度和塑性极限压力的表达式，即为本实验所要验证的目标公式.

图1 血管支架的单元和筋Fig.1 Cells and struts of the arterial stent

血管支架在撑开过程中，对称单元受到施加在内表面的压力p的作用，单元两端的截面产生了拉力F，在 F的作用下支架单元逐渐展开，如图2所示.

图2中:M为力偶;r为半径;α为单元弧度;b为筋宽;h为筋厚;hs为单元高度;L'为两端截面中心的曲面距离;β'为截面中心连线与水平线的夹角.

在不考虑支架材料的情况下，根据支架的空间结构支架和受力情况，在支架撑开的整个过程中，p与F的关系为

式中:β为假设弯曲支架筋拉直后与水平面的夹角.

图2 支架筋的几何尺寸、内表面压力和截面内力Fig.2 The geometrical dimension，inner pressure，and section internal forces of the strut

假设支架材料是理想弹塑性材料(弹性模量E、屈服应力σs)，提出了支架的弹性径向刚度和塑性极限压力的公式.弹性模量和屈服应力直接影响到支架性能和安全性.

支架的弹性径向刚度为

式中:L为弯曲支架筋拉直后的长度.

支架的塑性极限压力为

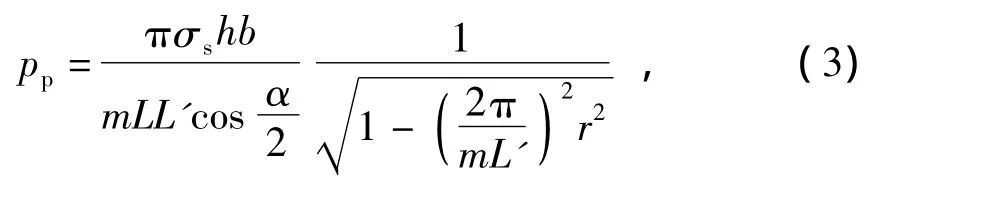
式中:m为每个主筋环段中对称单元的数量.

2 实验方法

2.1 实验原理

Dumoulin等分别采用了血管支架的三维弯曲模型和二维平面模型，对支架的撑开行为进行了有限元方法模拟:计算结果确认了二维平面模型良好的模拟效果，并且两种模型得到的支架的最大撑开直径的差值在5%以内，与支架制造商的实验数据吻合[12].Dumoulin等使用的二维模型实质上是三维弯曲模型的平面结构，可以看成三维平面支架的简化二维模型.

从支架的几何角度分析(如图2)，支架筋在垂直于轴向的平面上的弧度α比较小，支架单元在这个平面上的弯曲也很小，可以近似看作平面支架单元.

基于以上两点，本实验采用三维平面支架单元代替三维支架弯曲单元，对Yang等提出的支架弹性径向刚度和塑性极限压力进行实验验证.平面支架单元如图3所示，图中，三维弯曲支架筋曲面伸展为平面的结构，筋尺寸保持一致，平面单元在没有径向曲率后，通过单元侧向长度l与弯曲单元保持一致，有

本实验对平面单元施加外力F代替弯曲支架单元的外力压力p从而展开支架，外力F与弯曲支架的截面拉力F是对应的，因此，外力F与压力p的关系满足式(1).

图3 平面支架单元的尺寸和拉力Fig.3 The size of planar stent cell and tensile force on the cell

2.2 材料和仪器

本实验的三维平面支架单元试件采用铝合金材料，结构见图4.

试件材料通过拉伸实验测定其力学性能如图5所示.

图4 铝合金材料拉伸试件结构Fig.4 The tensile sample made of aluminum alloy

图5 铝合金试件拉伸应力-应变曲线Fig.5 The stress-strain curve of aluminum alloy specimen

由图5可知，其应力-应变曲线接近理想弹塑性材料，满足公式假设的材料力学性能，对应的弹性模量E=70 GPa，屈服应力σs=240 MPa.

实验中使用的平面单元初始几何尺寸如下:

l=8.64 mm，hs=24.80 mm，

h=2 mm，b=1.8 mm，

L=28.15 mm，L'=26.28 mm，

sin β'=0.9444 4，cos β =0.307.

对应的弯曲支架单元:

m=12，r=16.5 mm，α =π/6.

本实验的拉伸仪器采用MTS公司的伺服液压万能试验机，并采用配套的FlexTest控制器和数据采集软件记录实验数据.

2.3 实验方法

为了确保实验结果的准确性，对支架平面单元试件的侧表面性质进行验证，确认了试件侧表面平整规则且位于一个平面上，侧表面的单元几何形状与真实支架单元的平面形式几何结构保持一致.

将平面支架单元试件安装在MTS试验机上.把试件一边的固定端安装在试验机下端的楔形夹具上，使试件的拉伸轴线垂直于水平面.保持试件的拉伸轴线垂直于水平面，调整试验机的上端夹具并固定住试件的另一端.安装完成后的支架试件如图6所示.

图6 安装在楔形夹具上的平面支架试件Fig.6 The planar stent sample installed on the wedge-shaped fixture

使用MTS试验机的拉伸功能对试件进行加载并采集实验数据.支架试件固定之后，按照实验机的操作规范，控制加载速度，从0开始缓慢地对试件施加线性拉伸载荷，使支架试件的变形保持在准静态过程中.在支架加载过程中，利用实验控制系统采集实验数据，包括试件的拉伸载荷与对应的试件拉伸变形量.

3 结果验证

3.1 实验结果

在试验机的拉伸作用下，支架平面试件经历了与支架弯曲单元相似的变形.在球囊的扩张作用下，血管支架单元的变形表现为垂直于单元两端截面的拉伸扩展，两截面的拉伸方向夹角接近180°;平面支架试件的拉伸变形也是垂直两端截面的拉伸扩展，拉伸夹角呈180°.平面支架单元试件在拉力作用下的拉伸变形量如图7所示.

图7 支架平面单元试件拉伸变形量与拉力关系曲线Fig.7 The tensile force-deformation curve of the planar stent cell

鉴于支架平面单元和弯曲单元的关系和式(4)，弯曲单元的半径增量Δr和拉伸变形量Δl之间的关系为

根据式(1)，可以将支架平面双单元试件的实验数据转化为支架弯曲单元撑开过程的压力-半径曲线，如图8所示.

图8 平面支架结构单元压力-半径实验曲线Fig.8 The experimental pressure-radius curve of planar stent cell

由图8可以看出，支架单元经历了弹性撑开和塑性撑开，塑性撑开阶段特定半径对应的压力即是该半径下支架的塑性极限压力.

3.2 支架弹性径向刚度验证

按照式(2)，代入支架单元的几何参数和材料参数，可以得到公式预测的支架刚度为

kformula=0.175 MPa/mm.

由支架实验的弹性阶段数据可以计算出支架的弹性径向刚度为

kex=0.177 MPa/mm.

比较kformula和kex可知两者差值

(kex－kformula)/kex＜3%.

将弹性径向刚度公式预测的弹性阶段压力曲线与实验测量得到的压力-半径曲线比较(图9)，可以确定支架弹性径向刚度公式是正确的，且误差很小.

图9 平面支架单元弹性撑开阶段公式及实验曲线Fig.9 Comparison of pressure-radius curves between experiment and formula for the planar stent cell during elastic expansion stage

3.3 支架的塑性极限压力公式验证

将支架单元的几何参数和材料参数代入式(3)，可得支架的塑性极限压力和半径之间的关系.图10为实验测量的压力-半径曲线和公式预测的塑性压力曲线.

图10 平面支架单元塑性撑开阶段公式及实验曲线Fig.10 Comparison of pressure-radiud curves between experiment and formula for the planar stent cell during plastic expansion stage

通过与实验测量的曲线对比，发现公式预测的变化趋势与其保持一致，处于可接受的范围内，由此，通过实验验证了支架的塑性极限压力公式的准确性，且发现其精度较高.

4 讨论

血管支架的径向刚度和塑性极限压力等力学性质对支架在血管内的性能和安全起着重要的作用.支架一般需要高的径向刚度和强度来支撑病变的狭窄血管，以防支架植入后过大的血管回弹和支架坍塌;但是过高的径向刚度又容易造成血管的损伤[13-14].塑性极限压力随着支架半径的扩大而增大，代表了将支架打开到预定大小的难度.对于球囊扩张型支架，由于结构设计和材料因素导致的过高塑性极限压力对球囊提出了更高的要求，球囊需要在高内压下保持正常的扩张性能和更高的爆破压力.如果支架的塑性极限压力过低，临床手术中就极易出现支架过度膨胀的问题，可能引起心肌无复流、内膜增生、晚期官腔丢失和旁支血管堵塞等[15-17].

由于支架力学性质的重要性，所以有必要对支架径向刚度公式和塑性极限压力公式进行验证.文献[10-11]中用有限元方法对支架的径向刚度和塑性极限压力进行了验证，并没有采用实验验证.

在支架撑开实验方面，除形状记忆合金血管支架外，一般的血管支架的撑开需要借助于球囊膨胀的载荷.球囊的引入，使得实验中单纯分析支架的撑开力学行为变得困难.迄今为止，所有支架撑开力学性能实验研究都是在球囊参与下完成的，还没有支架自身力学性能实验评定方面的文献.本文中设计的平面支架单元，其实质是将支架膨胀变形变换成了平面支架的等效拉伸变形.在这种情况下，可以排除球囊加载的因素，实现对于支架结构本身的力学性能分析.

平面支架的载荷形式与真实支架有很大的不同.在本实验中，对平面支架采用拉伸实验，但从端头的夹持方式来分析，夹持载荷包括了拉伸力和抗弯曲的力矩.由于平面支架在长度方向上的非对称性，在拉伸力作用下，支架端面会发生转动，而本实验机采用的压紧夹持方式限制了端面转动，相当于给予了端面一个力矩.真实支架由于对称性而限制了端部截面的转动.平面支架被夹持的端面受力，与真实支架端部截面上的受力方式具有一致性.传统标准拉伸试件的夹持方式只能传递拉伸力，不能满足本实验的要求.

与真实支架相比较，本实验采用的平面支架，按几何比例大幅度增大了尺寸.真实支架尺寸筋宽和高为0.08 mm左右，目前一般的试验机很难做如此小尺寸的抗弯曲实验.从力学理论上讲，本实验中的尺寸放大可以模拟细小支架的情况.另一方面，0.08 mm筋尺寸有可能会产生尺度效应，影响到筋应力应变的本构关系，产生与大尺寸不一样的本构.在实际评估真实支架性能时，可以制作该尺寸下的长直筋，进行拉伸试验，通过简单拉伸实验确定微尺寸下的真实本构关系.

本实验对测定支架的力学性质的方法不但能够验证文献[10-11]提出的支架的力学公式，而且为支架结构的快速优化设计提供了途径.文献[10-11]提出的公式中材料假设为理想弹塑性材料，对应的支架主筋段是正弦波型，但是很多支架材料参数并不接近理想弹塑性，支架单元结构也差别很大.按照本实验的方法，可以根据目标支架的材料和结构，制造出平面单元试件，并进行拉伸测试等实验，从实验数据中分析支架的强度和压力极限等力学性质，有助于支架的优化设计和安全性分析.

5 结束语

本文提出了一种平面支架单元实验，并采用该实验方法对支架公式进行了检验.利用高精度的MTS实验机进行拉伸实验，并根据支架几何空间的特性，得到了血管支架的弹性径向刚度和半径-压力曲线，并与文献[10-11]提出的支架径向刚度和塑性极限压力进行对比，验证了这些力学公式有较高的精度，实验测量的弹性径向刚度和公式计算的弹性径向刚度差值在3%以内.

[1]ETAVE F，FINET G，BOIVIN M，et al.Mechanical property of coronary stents determined by using finite element analysis[J]. J. Biomechanics，2001，34:1065-1075.

[2]CHUA S N D，MACDONALD B J，HASHMI M S J.Effects of varying slotted tube(stent)geometry on its expansion behaviour using finite element method[J].J.MaterialsProcessing Technology， 2004， 155-156:1764-1771.

[3]MIGLIAVACCA F，PETRINI L，MONTANARI V，et al.A predictive study of the mechanical behaviour of coronary stents by computer modeling[J].Med.Eng.Phys.，2005，27:13-18.

[4]WALKE W，PASZENDA Z，FILIPIAK J.Experimental and numericalbiomechanicalanalysis ofvascular stent[J].J.Materials Processing Technology，2005，164-165:1263-1268.

[5]GERVASO F，CAPELLI C，PETRINI L，et al.On the effectsofdifferentstrategiesin modeling balloonexpandable stenting by means of finite element method[J].J.Biomechanics，2008，41:1206-1212.

[6]GARC A A，PE A E，MART NEZ M A.Influence of geometrical parameters on radial force during selfexpanding stent deployment.application for a variable radial stiffness stent[J]. Journal of the Mechanical Behavior of Biomedical Materials，2012，10:166-175.

[7]王晓，冯海全，王文雯，等.球囊扩张式冠脉支架生物力学性能研究[J].中国生物医学工程学报，2013，32:203-210.

WANG Xiao，FENG Haiquan，WANG Wenwen，et al.Research on biomechanics properties for balloonexpandable intracoronary stents[J].Chinese Journal of Biomedical Engineering，2013，32:203-210.

[8]WANG R，CHANDAR K R.Mechanical response of a metallic aortic stent-part Ⅰ: pressure-diameter relationshiop[J].Journal of Applied Mechanics，2004，71:697-705.

[9]程洁，周啸，李俐军，等.冠脉支架的多功能体外力学性能测试装置及实验研究[J].东南大学学报:自然科学版，2010，40(2):341-345.

CHENG Jie，ZHOU Xiao，LI Lijun，et al.In-vitro test apparatus and experimental study of mechanics properties of coronary stents[J].Journal of Southeast University:Natural Science Edition，2010，40(2):341-345.

[10]YANG J，HUANG N.Mechanical formula for the plastic limit pressure of stent during expansion[J].Acta Mechanica Sinica，2009，6:795-801.

[11]YANG J， HUANG N. Formula for elastic radial stiffness of the tubular vascular stent[C]∥6th World Congress on Biomechanics. Singapore: [s. n.]，2010:1435-1438.

[12]DOMOULIN C，COCHELIN B.Mechanical behaviour modelling of balloon-expandable stents[J].Journal of Biomechanics，2000，33:1461-1470.

[13]PARK W P，CHO S K，KO J Y，et al.Evaluation of stent performances using FEA considering a realistic balloon expansion[J].Proceedings of World Academy of Science:Engineering＆ Technolog，2008，37:117-122.

[14]DUERIG TW，WHOLEY M.A comparison of balloonand self-expanding stents[J]. Min Invas Ther ＆Allied Technol，2002，11(4):173-178.

[15]MAEKAWA Y，ASAKURA Y，ANZAI T，et al.Relation of stent overexpansion to the angiographic noreflow phenomenon in intravascular ultrasound-guided stent implantation for acute myocardial infarction[J].Heart Vessels，2005，20:13-18.

[16]ALEXANDRE Q，CARLOS A M G，EMERSON C P.Hyperexpansion of coronary stents and clinical outcomes[J].Texas Heart Institute Journal，2006，33:437-444.

[17]GREGG W S，FREDERICK G G，JOHN M H.Analysis of the relation between stent implantation pressure and expansion[J].The American Journal of Cardiology，1999，83:1397-1400.