直墙拱顶地下结构受爆炸地震波作用的动力响应
范鹏贤,王明洋,2,冯淑芳,王德荣,李 杰,2
(1.解放军理工大学爆炸冲击防灾减灾国家重点实验室,南京 210007;2.南京理工大学机械工程学院,南京 210094;3.沈阳军区司令部工程科研设计所,沈阳 110162)
直墙拱顶地下结构受爆炸地震波作用的动力响应
范鹏贤1,王明洋1,2,冯淑芳3,王德荣1,李 杰1,2
(1.解放军理工大学爆炸冲击防灾减灾国家重点实验室,南京 210007;2.南京理工大学机械工程学院,南京 210094;3.沈阳军区司令部工程科研设计所,沈阳 110162)
研究有弹性垫层的地下直墙拱顶结构在爆炸地震波作用下动力响应,采用共同变形理论及矩阵力法考虑衬砌与围岩的相互作用建立爆炸地震波作用的地下防护结构动力响应快速计算方法。分析围岩等级、垫层参数及荷载作用形式等对典型直墙圆拱结构动力响应影响。结果表明,围岩等级对结构动力响应具有显著影响,围岩质量越好结构位移、内力越小;垫层有延迟响应、降低响应峰值作用,荷载作用形式也有一定影响。
爆炸地震波;防护工程;直墙拱顶结构;动力响应
随新型钻地武器打击能力的提高,地下爆炸效应已对防护工程结构构成严重威胁。直墙拱顶地下结构为目前防护工程最常用工程结构形式。开展直墙拱顶地下结构在爆炸地震波作用下动力响应问题研究具有重要意义。利用试验、理论分析及数值模拟等对爆炸荷载作用的地下结构动力响应进行广泛研究[1-6]。我国的此项研究开展较晚,且主要集中于圆形结构,对直墙拱顶结构试验研究[7]及数值模拟成果[8-10]较少,难以满足工程设计与评估需求。
范鹏贤等[11]在矩阵力法理论基础上用集中质量方法将圆形隧道离散为有限自由度体系,将爆炸地震波作用视为作用于集中质量的动力建立地下圆形结构整体动力响应快速计算方法。本文采用矩阵力法,考虑衬砌与围岩间存在弹性垫层影响,建立地下直墙拱顶结构计算模型。利用算例分析围岩、垫层、荷载等参数对结构动力响应影响规律,为实际工程设计、评估提供参考。
1 计算模型及结构运动方程
1.1 计算模型
据防护工程常用坑道截面形式,选直墙拱顶结构为研究对象。设结构为岩土介质中钢筋混凝土封闭的拱形框架,存在弹性垫层时结构可视为双层弹性介质条件的工作框架。介质工作据弹性半空间模型考虑,结构承受几种爆炸波组合的联合作用。计算模型为含岩土介质、弹性垫层及钢筋混凝土框架相互作用的三部分,见图1,图中:1为钢筋混凝土框架,2为弹性垫层,3为动载荷。不考虑爆炸地震波在岩土介质中传播特性,将其对弹性垫层及结构作用视作动荷载加载到垫层上研究结构动力响应。
为研究结构强迫振动,用集中质量法将结构简化成有限自由度的离散体系见图2。每种地震爆炸波作用均以一系列作用于集中质量的动力代替,每个力均用波到达时间toi、波中最大压力σmi及随时间变化规律τi(τ)表示。

图1 结构模型简图Fig.1 The schematic diagram of structuralmodel

图2 单元及受力简图Fig.2 The elements and their force diagram
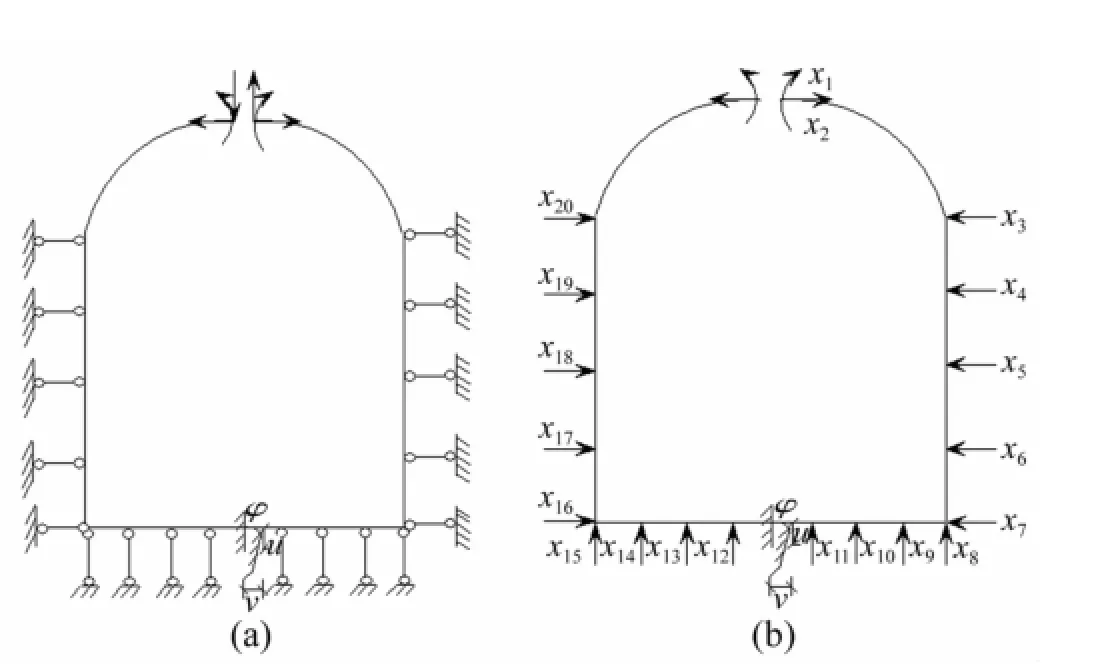
图3 链杆法计算简图Fig.3 The schematic diagram of Chain-bar Method
1.2 结构运动方程
对双层介层采用集中质量体系,考虑障碍物柔性强迫振动矩阵形式可写为
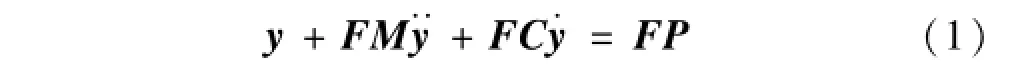
式中:P={Pi}26为动载荷列向量;M=[mij]26×26为集中质量对角线矩阵;F=[fij]26×26为集中质量单位位移矩阵;C为阻尼矩阵;y={yi}26,y··={y··}26分别为集中质量的位移及加速度向量。
1.2.1 荷载确定方式
动载荷列向量P以每个波k的列矩阵总和形式确定,即

式中:σkm,αk分别为第k个波到达时最大压力及角度;k0为波反射系数:v为围岩泊松比。
式(3)中向量Fk=[Fki]26各元素代表第k个波产生的动载荷随时间变化规律,可写为


式中:U为结构自身变形;y1,ij为弹性半空间变形;y3,ij为垫层变形;J为截面惯性距;A为截面面积;G2为材料剪切模量;γ为截面修正系数;Fij为未知力Xi作用下j点位移;h3为垫层材料泊松比;E3为垫层材料弹性模量;li为计算段长度。
由此可得确定系数矩阵B与自由项矩阵D的计算式为

1.3 求解方法
据以上各式用数值方法求解有限自由度体系强迫振动。在每个积分步长中对某个参数进行限制,使原始二阶方程式变为依次求解的一阶方程组,利用Fortran语言用四阶Rung-Kutta方法求解。方程组可写为

2 围岩等级对结构响应影响
2.1 算例参数设定
矩阵力法对求解地下圆形结构在爆炸地震波作用下动力响应中已获得成功应用[11],此处不重复验证。为考察围岩、垫层、荷载等对直墙拱顶结构动力响应影响,用本文方法计算典型直墙拱顶结构动力响应。直墙拱顶结构断面尺寸宽l=3.0 m,直墙高h=1.8 m,拱顶高f=1.2 m,衬砌结构厚h0=0.4 m。据资料取自由场荷载升压时间为28.1 ms,正压作用时间为200 ms,荷载峰值为3.02×105N/m2;钢筋混凝土结构弹性模量E=2.5×1010N/m2,结构材料密度ρ=2.55×103kg/m3。如无特殊说明,本文均采用此参数。
据《公路隧道设计规范》,选取典型围岩进行分析。其物性参数见表1。

表1 典型围岩物性参数Tab.1 Parameters of rocks
2.2 围岩参数不同时结构动力响应
围岩等级不同时拱顶位移时程曲线见图4。由图4看出,荷载与直墙垂直时拱顶产生向下的位移,围岩等级对隧道位移影响较显著,围岩特性越好阻抗比越大,拱顶位移越小,限制隧道位移能力越好;随围岩刚度的减小结构产生位移峰值时间明显延后。
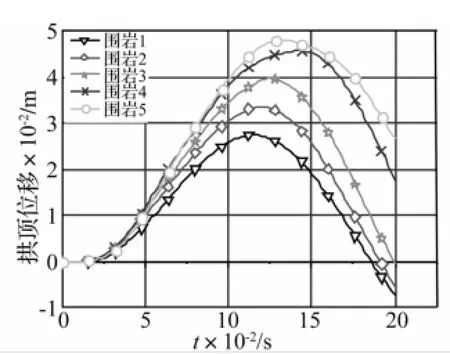
图4 拱顶竖向位移时程曲线Fig.4 The time-history curves of displacement of the arch top

图5 拱顶截面弯矩时程曲线Fig.5 The time-history curves of themoment of the arch top cross-section
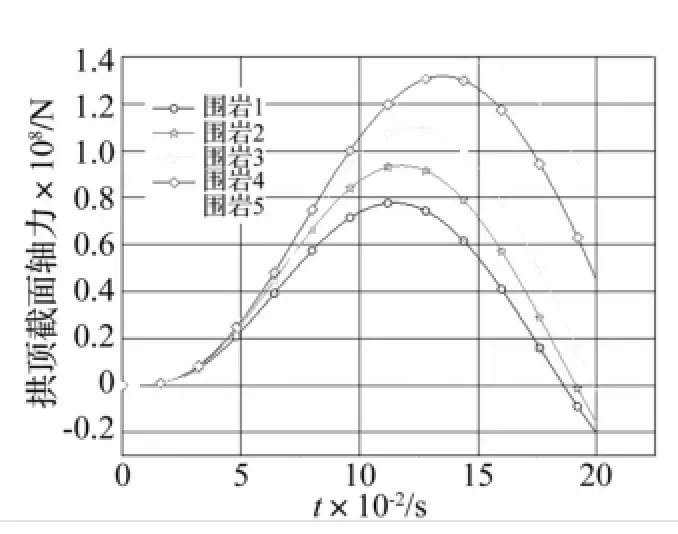
图6 拱顶截面轴力时程曲线Fig.6 The time-history curves of the axial force of the arch top cross-section
围岩等级不同时拱顶截面弯矩、轴力的时程曲线见图5、图6。由两图可知,围岩特性越好衬砌结构截面承受的内力越小。与衬砌拱顶位移时程(图4)比较知,围岩等级较差(围岩5)时衬砌拱顶位移峰值约为围岩等级较好(围岩1)的2倍,但相应截面轴力值相差约6倍,而弯矩相差超10倍。由此可见,爆炸地震波对地下结构内力影响远大于对结构位移影响。结构的弯矩、轴力为结构设计选择截面及配筋的重要依据,因此对结构截面动内力进一步研究十分必要。
3 垫层参数变化对结构响应影响
在结构与围岩间增加软垫层为防护工程常用隔振减震方法。为说明垫层对结构动力响应作用,本文模型考虑垫层变形影响,计算不同厚度垫层的结构动力响应。设衬砌厚度不变,分别计算衬砌厚度h=0.6 m,0.8 m,1.0 m,1.2 m,1.4 m时衬砌拱顶位移随时间变化曲线,见图7。由图7看出,设置垫层后拱顶位移明显减小,随垫层厚度增大衬砌达到位移峰值的时间延迟,峰值减小。此因设置垫层与围岩间波阻抗不匹配,冲击波在垫层与围岩之间产生反射,部分能量被反射,部分能量被垫层吸收,从而减小对结构的动力作用。而当垫层厚度与衬砌厚度比大于3时,增加垫层厚度对结构影响效果明显减小。

图7 垫层厚度变化时衬砌拱顶位移时程曲线Fig.7 The time-history curves of the displacement of the arch top cross-section under different subcrust conditions
有垫层衬砌拱顶截面环向应力与无垫层时最大应力值之比的时程曲线见图8。由图8看出,衬砌结构加入弹性垫层后因弹性垫层的消波作用,截面应力明显减小(10%~17%)。随垫层厚度增加影响越明显,且应力最大值出现时间明显滞后;但垫层厚度与衬砌厚度比大于3时,应力变化不再明显。可见垫层厚度并非越厚越好。设计中应综合考虑经济因素及抗爆效果。通常垫层弹性模量远小于衬砌结构。垫层较软时分析表明,垫层弹性模量对垫层抗爆隔振效果影响较小。

图8 拱顶截面环向应力与衬砌无垫层时最大应力比值时程曲线Fig.8 The time-history curves of the non-dimensional axial stress of the arch top cross-section under different subcrust conditions
4 荷载作用对结构响应影响
4.1 爆炸波入射角变化对结构响应影响
对衬砌、围岩荷载作用位置不变、爆炸波入射角由0°~90°变化时结构动力响应进行分析。
爆炸地震波入射角度变化时拱顶位移变化时程曲线见图9。由图9看出,入射角度增加拱顶位移越大,入射角大于45°后拱顶位移逐渐变小;入射角θ=90°时结构位移最小;入射角θ=45°时对结构位移影响最大。

图9 拱顶位移时程曲线Fig.9 The time-history curves of the displacementof the arch top cross-section

图10 拱顶弯矩时程曲线Fig.10 The time-history curves of the momentof the arch top cross-section
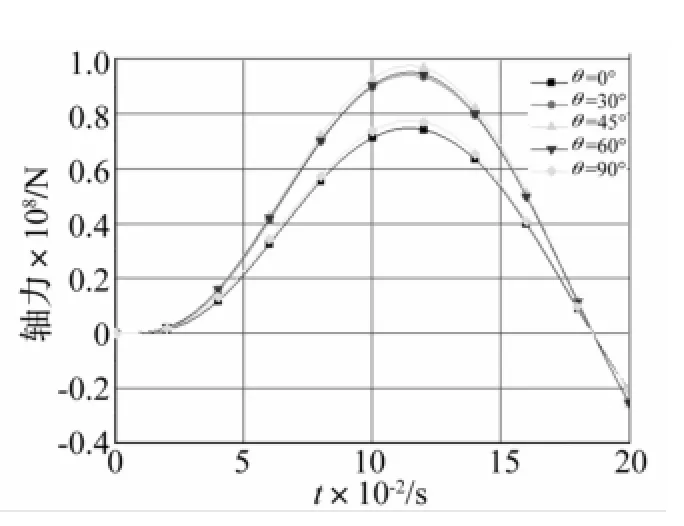
图11 拱顶轴力时程曲线Fig.11 The time-history curves of the axial force of the arch top cross-section
荷载作用位置变化时拱顶截面弯矩、轴力时程曲线见图10、图11。由二图看出,θ=0°时荷载对拱顶截面弯矩影响最大;θ=45°时拱顶产生反向弯矩,但拱顶截面轴力此时达最大。说明此时截面产生的应力最大,即同等荷载对结构产生的动力响应最大。
4.2 荷载正压作用时间对结构响应影响
正压作用时间对结构位移、应力亦有影响。增加正压作用时间结构位移、应力峰值会增加约10%,但位移、应力出现峰值的时间基本一致。增加荷载作用时间升压作用时间不变。正压作用时间增加时结构位移、应力变化基本一致。
5 结 论
据矩阵力法,考虑结构、垫层及围岩的相互作用,建立直墙圆拱结构动力响应计算方法;研究围岩特性、垫层参数及荷载作用形式对结构动力响应影响,结论如下:
(1)围岩等级对隧道动力响应影响显著,围岩特性越好,拱顶位移、内力越小;爆炸地震波对地下结构内力影响远大于对其位移影响。
(2)铺设垫层利于减小衬砌的位移及内力,增加垫层厚度衬砌达位移峰值时间有一定延迟;垫层厚度并非越厚越好。
(3)荷载作用位置不变、爆炸波入射角的变化对结构动力响应影响较大。本文所提方法及分析结果可为防护工程抗爆设计、评估提供参考。
[1]Akiyoloi T,Fuschida K.Soil-pipelines interaction through a frictional interface during earthquake[J].Soil Dynamic and Earthquake Engineering,1984,3(1):77-81.
[2]NateghiR,Kiany M,Gholipouri O.Control negative effects of blasting waves on concrete of the structures by analyzing of parameters of ground vibration[J].Tunneling and Underground Space Technology,2009,24(6):508-515.
[3]沈俊,顾金才,陈安敏,等.岩土工程抗爆结构模型试验装置研制及应用[J].地下空间与工程学报,2007,3(6):1077-1132.
SHEN Jun,GU Jin-cai,CHEN An-m in,et al.Evelopment and applications of themodel test apparatus on anti-explosion structures in geotechnical engineering[J].Chinese Journal of Underground Space and Engineering,2007,3(6):1077-1132.
[4]辛凯,姜忻良,吴祥云.爆炸荷载作用下两相饱和土中结构响应试验研究[J].岩石力学与工程学报,2009,28(S2):4065-4070.
XIN Kai,JIANG Xin-liang,WU Xiang-yun.Experimental study on structure response in two-phase saturated soil under blasting load[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(S2):4065-4070.
[5]高盟,高广运,王滢,等.均布突加荷载作用下圆柱形衬砌振动响应的解析解[J].岩石力学工程学报,2010,29(2):237-242.
GAOMeng,GAO Guang-yun,WANG Ying,etal.Analytical solution on dynamic response of lining subjected to sudden internal uniform loading[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(2):237-242.
[6]Feldgun V R,Kochetkov A V,Karinski Y S,et al.Blast response of a lined cavity in a porous saturated soil[J].International Journal of Impact Engineering,2008,35:953-966.
[7]杨自友,顾金才,陈安敏,等.锚杆长度对洞室抗爆性能影响的模型试验研究[J].振动与冲击,2009,28(1):24-27.
YANG Zi-you,GU Jin-cai,CHEN An-min,et al.Model experiment study on the influence of anti-blast characteristics of length of rock bolts in wall rock ofunderground cavern[J].Journal of Vibration and Shock,2009,28(1):24-27.
[8]国胜兵,王明洋,赵跃堂,等.爆炸地震波作用下地下结构动力响应数值分析[J].世界地震工程,2004,20(4):137-142.
GUO Sheng-bing,WANG Ming-yang,ZHAO Yue-tang,et al.Dynamic numerical analysis of underground structures under action of exp losion seism ic wave[J].World Information on Earthquake Engineering,2004,20(4):137-142.
[9]孙惠香,许金东.爆炸荷载作用下地下结构与围岩的动力响应[J].土木工程学报,2011,44(S):148-152.
SUN Hui-xiang,XU Jin-dong.Dynamic action study between structure and rock of underground structure subjected to blast load[J].China Civil Engineering Journal,2011,44(S):148-152.
[10]邓春梅,许金余,沈刘军.装药爆炸下地下拱形结构变形及破坏特征分析[J].解放军理工大学学报(自然科学版),2007,8(5):534-537.
DENG Chun-mei,XU Jin-yu,SHEN Liu-jun.Deformation and damage characteristics analysis of underground arch structure subjected to subsurface blast[J].Journal of PLA University of Science and Technology(Natural Science Edition),2007,8(5):534-537.
[11]范鹏贤,王明洋,冯淑芳,等.爆炸地震波作用下深埋圆形隧道的动力响应分析[J].岩石力学与工程学报,2013,32(4):671-680.
FAN Peng-xian,WANG Ming-yang,FENG Shu-fang,et al.Dynamic response of deep-buried circular tunnel to explosion seismic wave[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(4):671-680.
[12]王瑞民,华毅杰,武建勋.半空间地下结构与土相互作用的链杆法研究[J].同济大学学报,1999,27(4):495-498.
WANG Rui-m in,HUA Yi-jie,WU Jian-xun.Chain-bar method analysis of soil and underground structure interaction in semi-space[J].Journal of Tongji University,1999,27(4):495-498.
[13]Kerr A D.Elastic and viscoelastic foundation models[J].Journal of Applied Mechanics,1964,31:491-498.
Dynam ic response of underground straight-wall-round-arch structure subjected to explosion seism ic wave
FAN Peng-xian1,WANGMing-yang1,2,FENG Shu-fang3,WANGDe-rong1,LIJie1,2
(1.State Key Laboratory of Disaster Prevention&Mitigation of Explosion&Impact,PLA University of Science and Technology,Nanjing,Jiangsu 210007,China;2.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing,Jiangsu 210007,China;3.Institute of Engineering Research and Design,Headquarters of Shenyang Military Area,Shenyang 110162,China)
The dynamic response of underground structure impacted by explosion is of great importance in the designing and evaluating of the protective engineering.The computational method for the dynamic response of straightwall-round-arch structure subjected to explosion seismic wave was investigated on the foundation of common deformation theory and matrix forcemethod,and a rapid computation method was established.By the presented method,the dynamic responses of a typical straight-wall-round-arch structure were studied under different surrounding rock,subcrust and impact loading conditions.The results show that the rock grade,the thickness of subcrust and the loadingmode all have notable influences on the structure's dynamic response.The better quality the rock is of the lower the displacementand the internal force will be.And as the thickness of the subcrust increases,the peak value of the dynamic response decreases and delays.
explosion seismic wave;protective engineering;straight-wall-round-arch structure;dynamic response
TU352;TU 928
:A
10.13465/j.cnki.jvs.2014.22.033
国家自然科学创新研究群体科学基金(51021001);博士后科学基金面上项目
2013-01-17 修改稿收到日期:2013-11-28
范鹏贤男,博士,讲师,1983年生

