基于奇异值分解及特征正交分解的结构损伤检测方法
杨 斌,程军圣
(湖南大学汽车车身先进设计制造国家重点实验室,长沙 410082)
基于奇异值分解及特征正交分解的结构损伤检测方法
杨 斌,程军圣
(湖南大学汽车车身先进设计制造国家重点实验室,长沙 410082)
为直接通过结构振动响应提取损伤特征参数,将奇异值分解和特征正交分解运用到结构响应分析中。该方法首先通过对结构响应功率谱矩阵的奇异值分解,获得模态频率,然后在模态频率处计算互相关矩阵,利用特征正交分解获得收敛于结构模态向量的特征正交模态,进而构建了损伤定位向量,最后通过结构单元应力的不同分布准确定位了损伤位置。实验数据分析结果表明,该方法能有效的进行损伤检测和定位。
特征正交分解;奇异值分解;损伤定位向量;结构损伤检测
基于振动响应的结构损伤检测方法得到广泛研究及应用。传统的损伤检测方法主要通过结构损伤前后模态参数变化识别损伤,如固有频率、模态振型、模态柔度及模态应变能等。其中,基于模态柔度变化的损伤检测方法较有效,仅需前几阶模态参数即可获得准确的损伤检测结果,因此应用较广[1-2]。Bernal[3]在结构模态柔度变化基础上提出基于损伤定位向量(Damage Locating Vector,DLV)的检测方法,可更好体现柔度变化及结构损伤间内在联系。为比较结构损伤前后模态参数变化通常需对结构进行模态参数识别,以获取准确的结构模态参数;但某些情况下结构激励不易获取,较难通过传统模态参数识别方法获取准确的模态参数,无法判断结构状态。特征正交分解(Proper Orthogonal Decomposition,POD)在结构振动响应分析中得到广泛应用。该方法通过分析结构响应矩阵,获得能有效表征结构振动特性的特征正交模态(Proper Orthogonal Modes,POM),无需进行模态参数识别,适用于处理激励未知的运行工况下结构损伤检测。Feeny等[4]将POD方法用于振动响应分析,通过分解振动响应矩阵,获得能有效表征结构振动特性的特征正交模态。Galvanetto等[5]将POD方法用于损伤检测,通过对比损伤前后POM变化进行损伤识别及定位。Han等[6]研究认为仅当结构质量矩阵正比于单位矩阵时POD分解所得POM才会收敛于结构模态向量。结构发生损伤时若质量矩阵发生变化,POD分解所得POM将会极大偏离模态向量,无法准确反映结构的固有属性。因此又提出滤波POD分解方法;但该方法不能处理谐波频率情况,易得错误模态参数[7]。
本文提出基于奇异值分解(Singular Value Decomposition,SVD)及特征正交分解的损伤检测方法,对结构响应功率谱密度矩阵进行SVD分解,据奇异值曲线识别有效的模态频率,在模态频率处计算互相关函数,通过该函数矩阵的POD分解获得收敛于结构模态向量的POM。通过模态频率及POM构建柔度指标,由柔度变化矩阵获得损伤定位向量,再由结构单元应力的不同分布准确定位损伤位置。并通过实验结果验证该方法的有效性。
1 基于奇异值分解的特征正交分解在结构振动响应分析中应用
特征正交分解为简单有效的结构振动响应分析方法。通过对结构振动响应矩阵进行特征正交分解,可得能有效表征结构振动特性的特征正交模态。
设结构测点数L,采样点数N,得结构响应矩阵为

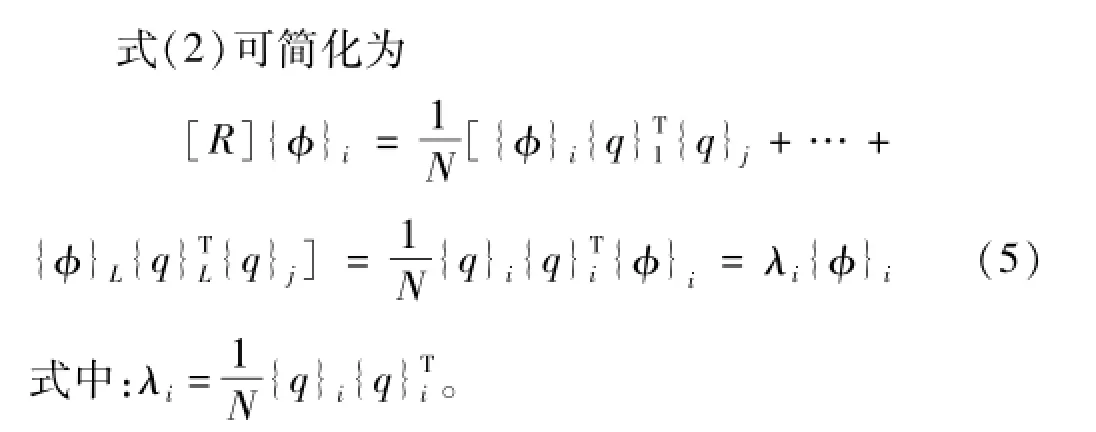
由此可见,结构质量矩阵正比于单位矩阵时,结构响应协方差矩阵特征向量即为模态向量。由特征正交分解所得特征正交模态收敛于模态向量;但实际结构中难以获知结构的质量矩阵,较难满足结构质量矩阵正比于单位矩阵。若结构质量矩阵不正比于单位矩阵,则式(4)不成立,因此无法得到式(5)。结构响应矩阵特征正交分解所得特征正交模态不收敛于结构模态向量,不能准确反映结构的固有特性。
为克服特征正交分解不足,本文提出基于奇异值分解及特征正交分解的模态向量提取方法。对结构响应功率谱矩阵进行奇异值分解,通过奇异值曲线获得模态频率,在模态频率处积分得协方差矩阵,对协方差矩阵进行特征正交分解,可得收敛于模态向量的特征正交模态。用频域分解方法对结构响应功率谱矩阵进行奇异值分解,不仅有效识别模态频率,且能识别由谐波频率所致虚假模态,因而在模态分析中应用广泛[8]。
设结构激励为x(t),则结构响应功率谱矩阵为
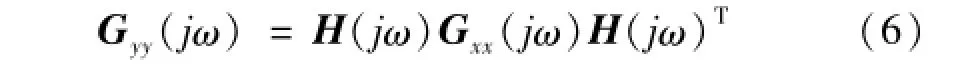
式中:Gxx(jω)为激励功率谱矩阵;Gyy(jω)为响应功率谱矩阵;H(jω)为频响函数矩阵。
频响函数矩阵可表示成分式形式为

式中:dk为常数。
对结构响应功率谱矩阵进行SVD分解,通过奇异值曲线峰值可有效识别模态频率。在模态频率处结构振动响应只含该阶模态响应。在第i阶模态频率ωi处结构振动响应矩阵可表示为
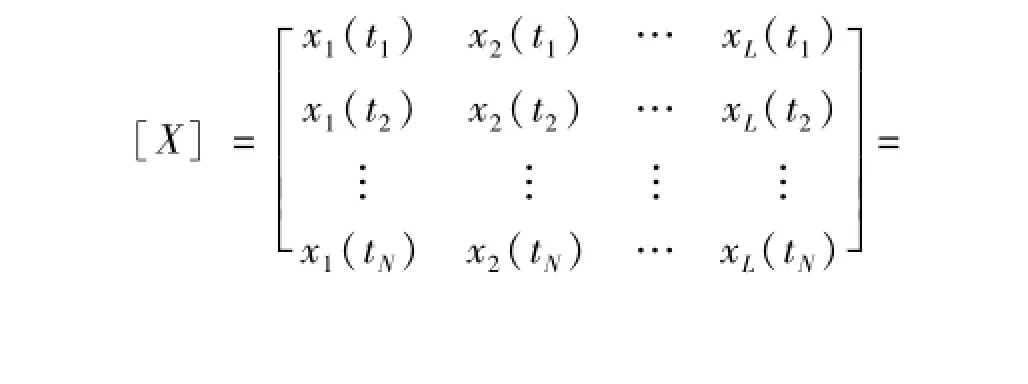

由式(10)可见,在模态频率处通过对结构响应矩阵进行特征正交分解,所得特征正交模态收敛于结构模态向量。
2 基于柔度变化的损伤定位向量法
该方法较固有频率及模态振型对结构损伤更敏感,且只需前几阶模态即可获得准确损伤检测结果。而基于损伤定位向量的损伤检测方法[9]能更好体现柔度变化及结构损伤间内在联系。其原理为:设有一特殊载荷向量,在该载荷作用下损伤前后结构位移不发生变化,即结构损伤单元处无应力产生。当此载荷向量施加于正常状况结构时计算单元应力,单元内力为零的单位即为损伤单元。计算步骤为:
(1)通过模态参数计算柔度矩阵,即

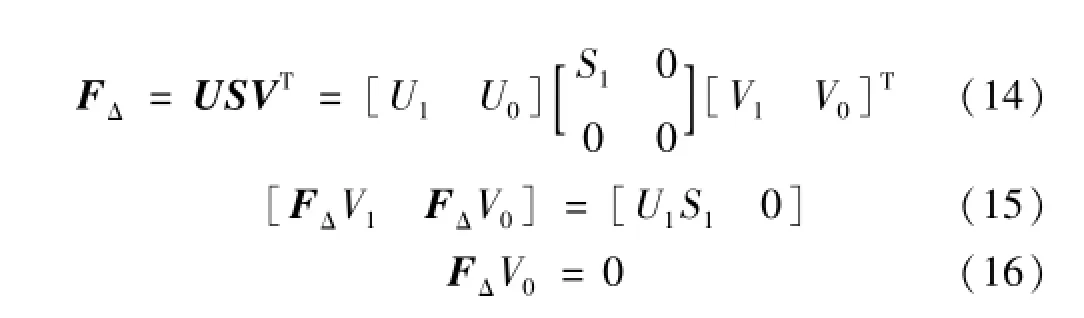
由式(16)知,载荷向量L=V0,即载荷向量可由柔度变化矩阵的奇异值分解获得。
(4)将所得载荷向量L施加于正常状况结构,计算、比较结构各单元应力σj,确定损伤单元。
实际情况中因测量误差及噪声影响,单元应力计算结果不为零,可通过较小单元应力指示损伤单元。
3 应用
本文用桁架结构实验数据[10]验证该方法的有效性。桁架结构由钢管通过螺栓搭接而成,见图1。激振器在垂直方向对结构施加白噪声激励。加速度传感器通过磁座安装于桁架结构,垂向布设13个振动加速度传感器,分别采集正常状态及损伤状态结构振动信号。采样频率250 Hz,采样点数1 024。通过减小钢管部件横截面积在单元4上设置40%的刚度减少模拟损伤。结构正常状态最左端传感器加速度响应见图2。
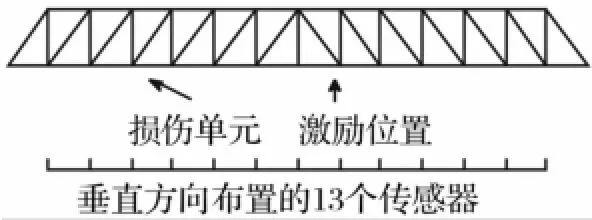
图1 桁架结构示意图Fig.1 The truss structure
计算各测点响应组成的功率谱矩阵,对功率谱矩阵进行奇异值分解,通过奇异值曲线确定模态频率。在每个频率下对结构响应功率谱矩阵Gyy(jω)进行奇异值分解,得奇异值δ1≥δ2≥…≥δn,取每个频率ω下前4阶奇异值,结构响应功率谱矩阵奇异值曲线见图3。选奇异值最大的前3阶模态频率为ω1=20.1 Hz,ω2=41.2 Hz,ω3=62.0 Hz
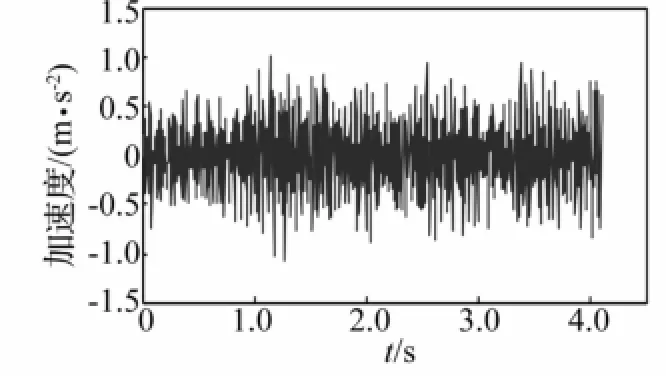
图2 结构正常状态下振动响应Fig.2 The structural response under normal condition
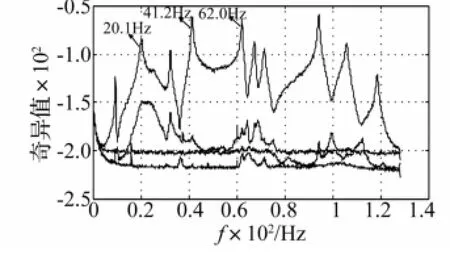
图3 结构响应功率谱奇异值曲线图Fig.3 The singular value curve of the response power spectrum
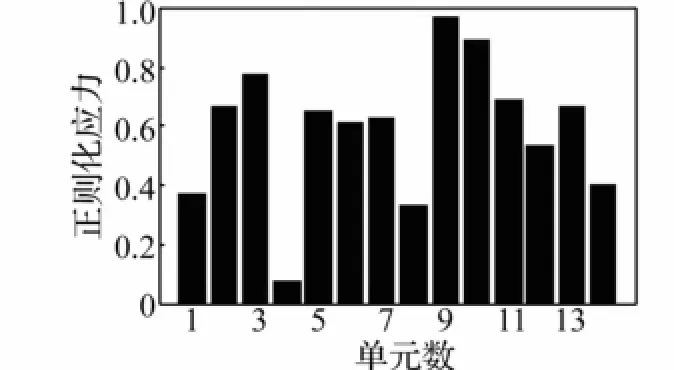
图4 结构单元应力分布Fig.4 The stress distribution of different element
在各阶模态频率附近选若干谱线,相加后即可得到该频率处互相关矩阵,并对该矩阵进行特征正交分解得到特征正交模态。通过模态频率及特征正交模态构建柔度指标,计算损伤前后柔度变化矩阵。对柔度变化矩阵进行奇异值分解,通过式(14)求得载荷向量,进而通过有限元模型求得结构损伤单元所在列各单元应力(图4),比较各单元应力确定损伤单元为第4单元。由此可见,基于奇异值分解及特征正交分解的结构损伤检测方法能有效检测结构损伤及位置。
4 结 论
(1)本文将奇异值分解与特征正交分解结合用于结构损伤特征参数提取。通过对结构响应功率谱矩阵的奇异值分解获得模态频率,计算互相关矩阵;并对其特征正交分解获得收敛于结构模态向量的特征正交模态,通过对模态频率和特征正交模态组成的柔度矩阵奇异值分解,构建损伤定位向量;通过结构各单元应力分布对结构损伤位置做出准确判断。实验数据结果表明,该方法能准确检测结构损伤及损伤位置。
(2)该方法存在局限性。通过结构响应功率谱奇异值曲线峰值拾取只适用简单结构的模态频率识别,复杂结构模态频率辨识仍需进一步模态参数识别过程;因基于损伤定位向量的损伤检测方法在检测损伤位置时需先建立结构准确有限元模型,故实际应用中受限制。
[1]杨秋伟,刘济科.工程结构损伤识别的柔度方法研究进展[J].振动与冲击,2011,30(12):147-153.
YANG Qiu-wei,LIU Ji-ke.Structural damage identification with flexibility changed:a review[J].Journal of Vibration and Shock,2011,30(12):147-153.
[2]曹晖,张新亮,李英民.利用模态柔度曲率差识别框架的损伤[J].振动与冲击,2007,26(6):116-120.
CAO Hui,ZHANG Xin-liang,LIYing-min.Damage evaluation of frames by modal flexiblity curvature[J].Journal of Vibration and Shock,2007,26(6):116-120.
[3]Bernal D.Load vectors for damage localization[J].Journalof Engineering Mechanics,2002,128(1):7-14.
[4]Feeny B F,Kappagantu R.On the physical interpretation of proper orthogonalmodes in vibrations[J].Journal of Sound and Vibration,1998,211(4):607-616.
[5]Galvanetto U,Violaris G.Numerical investigation of a new damage detectionmethod based on proper orthogonal decomposition[J].Mechanical Systems and Signal Processing,2007,21(3):1346-1361.
[6]Han S,Feeny B.Application of proper orthogonal decomposition to structural vibration analysis[J].Mechanical Systems and Signal Processing,2003,17(5):989-1001.
[7]Jacobsen N J.Separating structuralmodes and harmonic components in operational modal analysis[C].Conference:IMAC-XXIV:Conference&Exposition on Structural Dynamics,2006.
[8]Brincker R,Zhang L M.Modal identification of output-only systems using frequency domain decomposition[J].Smart Materials and Structures,2001,10(3):441-445.
[9]Gao Y,Spencer B F.Experimental verification of the flexibility-based damage locating vectormethod[J].Journal of Engineering Mechanics,2007,133(10):441-445.
Structure damage detection method based on singular value decom position and proper orthogonal decom position
YANG Bin,CHENG Jun-sheng
(State key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University,Changsha 410082,China)
To extract the sensitive damage features directly from the structural vibration responses,the singular value decomposition and the proper orthogonal decomposition were applied to decompose the structural vibration response matrix into a set of proper orthogonal modes,which can represent the structure natural properties.The singular value decomposition was applied on the structural vibration power spectralmatrix to figure out the modal frequencies,then at eachmodal frequency the correlation matrix was calculated.The proper orthogonal decomposition was applied on the correlation matrix calculated to get the proper orthogonalmodes which can converge to the normal structuralmodes.The proper orthogonalmodeswere used to construct a damage locating vector,and to determine the damage location through inspecting the different stress distribution in each element.The experimental results show that the proposed method can detect and locate the damage effectively.
proper orthogonal decomposition;singular value decomposition;damage locating vector;structure damage detection
TH113.1
:A
10.13465/j.cnki.jvs.2014.22.029
国家自然科学基金(51075131);湖南省自然科学基金(11JJ2026)
2013-02-05 修改稿收到日期:2013-12-19
杨斌男,博士生,1987年10月生
程军圣男,教授,博士生导师,1968年10月生邮箱:signalp@tom.com

