二维矩形月池内流体自振特性研究
黄 磊,刘利琴,唐友刚
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
二维矩形月池内流体自振特性研究
黄 磊,刘利琴,唐友刚
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
研究二维矩形月池流体的自振特性。基于线性势流理论,采用Galerkin展开,将问题转化为月池自振频率特征值问题,求解自振频率及速度势函数的系数矩阵,获得二维矩形月池固有频率及振型的半解析解,分析月池几何参数对月池流体自振特性影响。研究表明,由于内部与外流连通,月池流体呈垂向活塞(piston)振动及晃荡(sloshing)运动两种形式。垂向活塞振动模态频率变化主要受液面高度影响,且随液面高度增加而减小;晃荡模态频率主要受月池宽度影响,随月池宽度增加而减小。活塞振动模态振型在液面较浅时出现波峰,随液面高度增加而消失。利用CFD方法计算月池运动,结果与半解析解中振型曲线拟合良好。
月池;半解析解;自振特性;势流理论
钻井船、FPSO及Spar平台等海洋结构物常据实际需要布置垂直方向贯穿结构主体的月池结构,立管及其它钻井设施穿过月池通向海底,以避免遭受过大波流载荷激励[1-3]。由于底部开口,月池内流体运动存在两类固有振荡形式,即流体沿深度方向“活塞(piston)”振动及流体液面左右“晃荡(sloshing)”运动[4-6]。针对月池内流体的振动特性及复杂海洋环境中月池流体与结构的耦合运动已开展相关研究。如Aalbers[7]将月池内水柱的活塞振荡处理为弹簧-质量系统,研究波浪作用的船体发生垂向运动时月池内流体活塞振动,分析月池内水柱活塞振荡特性对船舶垂荡运动影响。结果表明,月池能有效降低船舶垂荡运动,改善其运动特性。Molin[8]假设无限水深静止船舶的矩形月池,用简化的准解析法研究月池中流体活塞振荡、晃荡运动的固有振动特性,给出液舱内流体活塞振动、晃荡的一阶固有频率近似表达式,并模拟月池内二、三维自由液面形状。Faltinsen等[9]对有限水深条件下二维矩形月池建立线性势流方程,通过求解域分解,利用伽辽金法研究船舶小幅辐射运动对月池活塞振荡运动的解析解。Kristiansen等[10-12]利用CFD建立二维月池模型,研究非线性自由液面、边界阻尼及流动分离对月池活塞振荡影响,结果表明流动分离是造成线性势流理论结果高于实验测量数据的主要原因。姚熊亮等[13-14]通过实验研究圆形月池在波浪条件下的流激振荡特性。周华伟等[15]据势流理论研究具有月池的圆柱结构辐射与绕射问题。Zhang等[16]通过分解求解域方法研究两层流中的月池运动问题。
本文在文献[8]基础上,基于线性势流理论研究二维矩形月池的活塞振动、晃荡运动特性,分析月池几何参数对月池流体自振特性影响,利用CFD软件模拟月池运动对比解析解振型曲线,研究成果可为相关计算分析及结构设计提供参考依据。
1 数学模型建立
月池长度远大于宽度时,长度方向对月池自振特性影响较小。因此可将月池简化为二维形式。考虑的二维矩形月池宽度b,液面高度h,月池底部完全开放。建立坐标系,原点o位于月池底部左下角,见图1。

图1 二维矩形月池坐标系Fig.1 Coordinate of a two dimensional rectanglemoonpool
设船舶具有无限长宽且静止不动,月池内流体为无粘、无旋、不可压缩的理想流体,据线性势流理论,得月池内流体控制方程为



2 数值计算结果
2.1 系数矩阵数值计算
本文利用复化辛浦生算法[17],数值计算式(13)中二重积分得系数tmn,并将计算结果与采用Molin计算方法[8]所得结果进行对比,见图2。由图2看出,两种计算方法所得结果吻合较好。
2.2 固有振动频率
通过Galerkin展开将计算月池的固有振动特性问题转化为计算式(18)的特征值问题。截取适当阶次,即可得各阶频率近似解。其中0阶代表月池的piston模态,奇数阶代表反对称sloshing模态,其余偶数阶代表对称sloshing模态。取月池宽b=20 m、液面高h分别为1 m、10 m时,不同截断阶次N对应的piston模态及前三阶sloshing模态频率见表1、表2。由二表看出,各阶频率收敛速度均较快。

表1 b=20 m,h=1 m不同截断阶次下各阶模态频率Tab.1 b=20 m,h=1m,Piston and sloshingmode frequencies for d ifferent truncation order
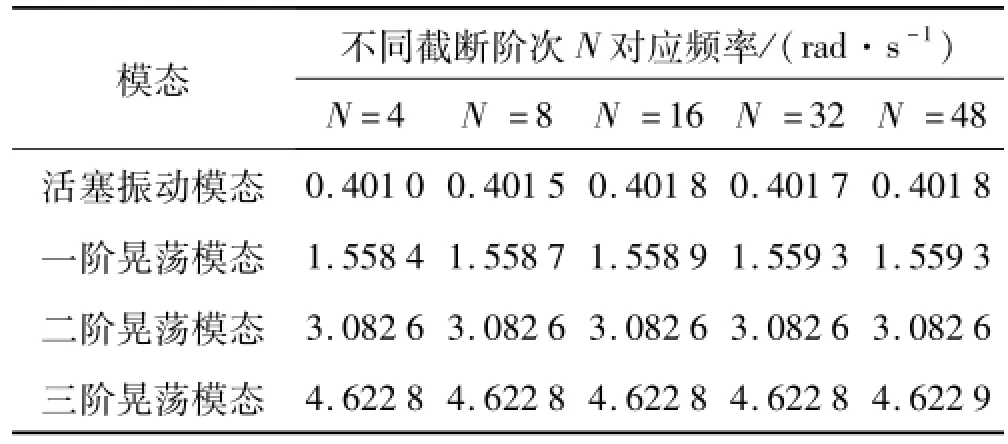
表2 b=20 m,h=10m不同截断阶次下各阶模态频率Tab.2 b=20 m,h=10 m,Piston and sloshing mode frequencies for different truncation order
月池宽度b分别为10 m、20 m时piston模态频率及1、2阶sloshing模态频率随月池液面高度h的变化曲线见图3~图6。

图2 积分结果对比Fig.2 Integration value comparison

图3 自振频率随h变化(b=10 m)Fig.3 Natural frequency change versus h(b=10 m)
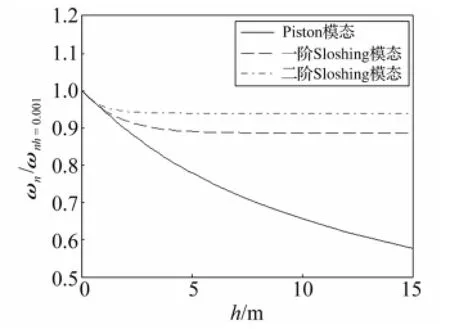
图4 自振频率比值随h变化(b=10 m)Fig.4 Ratio of natural frequency change versus h(b=10 m)
图3为各阶自振频率随液面高度h变化曲线。由图3看出,Piston模态频率为最低阶模态。此阶模态振动时月池内流体整体上下运动,随液面高度增加流体质量持续增加,自振频率随之降低。而各阶sloshing模态主要由自由液面左右晃动激励时产生,液面高度变化不影响sloshing模态,各阶sloshing曲线为水平平行;但液面高度较低时自由液面位置离月池底部较近,sloshing频率会随h增高而降低,由于月池底部开放内外相连,流体流动对自由液面运动产生耦合作用。由此知,月池水平运动时底部开放对月池内流体影响范围较小,离月池底超5 m以上的流体已基本不受底部流体流动影响。
图4为对应不同液面高度h的各阶自振频率与h=0.001 m时自振频率比值变化曲线。由图4可清晰看出各阶频率变化率。h较小时频率下降速度相同,此时底部流体流动明显主导各阶模态变化;而随h升高,仅piston模态频率持续下降,其它各阶sloshing模态频率不变化。
图5、图6为月池宽度20 m时两组频率随h变化曲线。与图3、图4对比看出,月池宽度增加未改变自振频率随h的变化规律。由此可见,液面高度h为决定pinston模态频率的关键参数,而对sloshing模态频率影响较小。由于piston模态频率随h持续降低,h较高时piston模态自振频率可能接近平台自振频率及波浪入射频率,应特别关注。图7为液面高度1 m时月池各阶自振频率随月池宽度变化曲线。由图7看出,月池宽度从1 m增长至15 m时各阶频率均逐渐减小,超过15 m后频率变化趋于平稳。对比各曲线知,sloshing模态频率随宽度变化率高于piston模态。图8为各高度频率与液面1 m高频率比值变化曲线。由图8看出,各阶sloshing模态频率随月池宽度变化率相同,均高于piston模态频率。
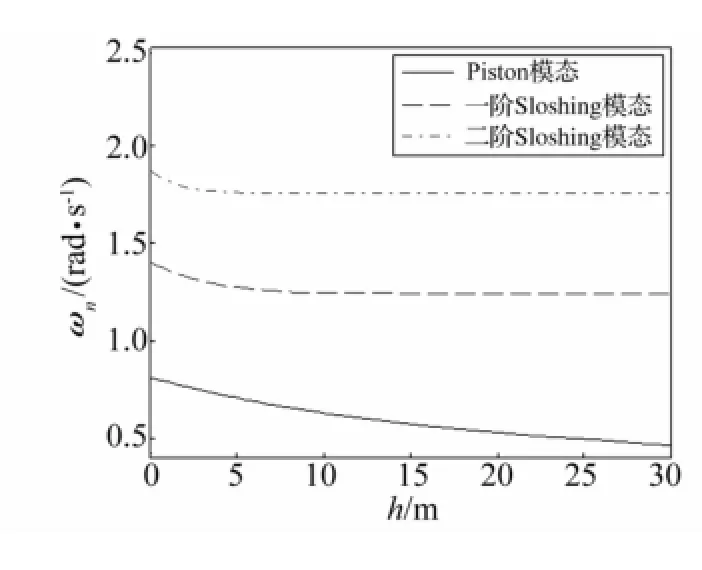
图5 自振频率随h变化(b=20 m)Fig.5 Natural frequency change h(b=20 m)

图6 自振频率比值随h变化(b=20m)Fig.6 Ratio of natural frequency change versus versus h(b=20 m)

图7 自振频率随b变化(h=1m)Fig.7 Natural frequency change versus b(h=1m)
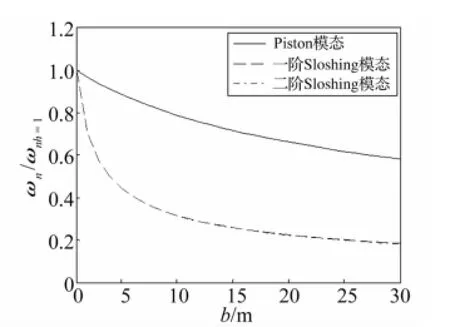
图10 自振频率比值随b变化(h=10 m)Fig.10 Ratio of natural frequency change versus b(h=10m)
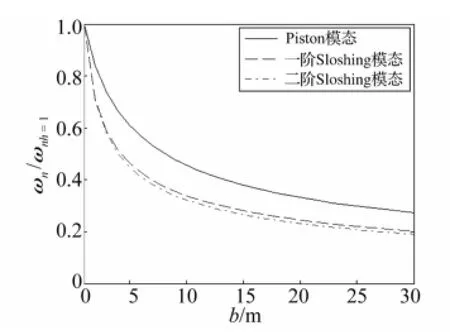
图8 自振频率比值随b变化(h=1 m)Fig.8 Ratio of natural frequency change versus b(h=1m)

图9 自振频率随b变化(h=10 m)Fig.9 Natural frequency change versus b(h=10m)
图7、图8中月池液面较浅,宽度高于液面高度,该形式月池在钻井船、FPSO等结构中较常见。而对深水SPAR平台月池,其液面较高与月池长度相当,甚至高于月池长度。图9~图12为液面高度10 m、20 m时自振频率随月池宽度变化曲线。由图9看出,b<10 m时sloshing模态频率下降较明显;b>10 m后随宽度继续增加sloshing模态频率变化逐渐平缓。piston模态曲线则始终变化较小,曲线形状较平缓。对比图11可知,液面高度20 m时自振频率随月池宽度变化与图9中液面高度10 m曲线具有完全相同规律。图10为不同月池宽度时各阶自振频率与b=1 m时比值变化曲线。由图11看出,各阶sloshing频率随宽度增加变化规律完全相同,且变化速度由快变慢。对比图12看出,液面高度增加未影响此变化规律。
由图9~图12可知,月池宽度对sloshing模态频率影响非常明显,此为sloshing模态由自由液面运动所致。月池宽度变化对自由液面形状产生直接影响,因此自振模态频率发生明显变化。液面较低时自由液面离底部较近,其运动会受由底面流体流动影响,但范围有限。而对垂直方向振动的piston模态频率,基本不受月池宽度变化影响。
2.3 自由液面
将由式(18)所得各阶特征值对应的特征向量矩阵B代入式(19)得矩阵A。将矩阵A、B代入式(9)及自由液面方程

式中:η为波面升高。
由式(20)可得各阶自振频率对应振型。
图13~图15为20 m宽月池不同液面高度时piston模态及1~3阶sloshing模态对应振型。由三图看出,piston模态呈活塞运动特性,波面整体升高偏离平衡位置;sloshing模态奇数阶为反对称振型,偶数阶为对称振型,波面曲线在平衡位置具有三角函数特征。

图11 自振频率随b变化(h=20m)Fig.11 Natural frequency change versus b(h=20 m)

图12 自振频率比值随b变化(h=20m)Fig.12 Ratio of natural frequency change versus b(h=20 m)

图13 b=20m,h=0.02 m时月池各阶模态振型Fig.13 Free surface shape for different orders when b=20 m,h=0.02 m

图14 b=20 m,h=2 m时月池各阶模态振型Fig.14 Free surface shape for different orderswhen b=20 m,h=2m
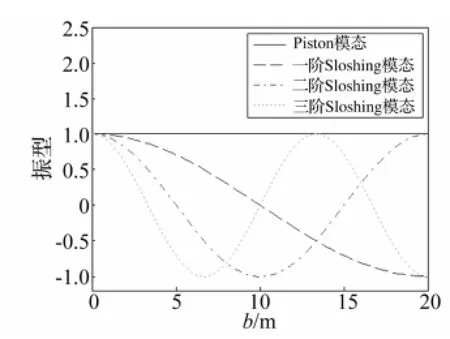
图15 b=h=20 m时月池各阶模态振型随h变化Fig.15 Free surface shape for different orderswhen b=h=20m

图16 b=20 m时piston模态振型Fig.16 Free surface shape of piston mode for different h when b=20 m
对比图13~图15看出,不同液面高度振型具有明显差异。h=0.02 m时液面较低,sloshing模态各阶振型在接近月池两侧壁处出现波峰,piston模态在月池宽度方向出现波峰。当液面高度达到2 m时波峰逐渐减小,低阶频率波峰仍存在,而高阶频率此现象已消失。该现象因底部流体流动所致。piston模态液面较低,液柱在垂向振动时,液面向上或向下会出现波峰,而高液面时,液面完全呈平面,在平衡位置上下振动。sloshing模态随液面高度增加底面流动对其影响衰减较迅速。底面流动对自由液面形状影响随h减小速度高于对频率影响减小速度。
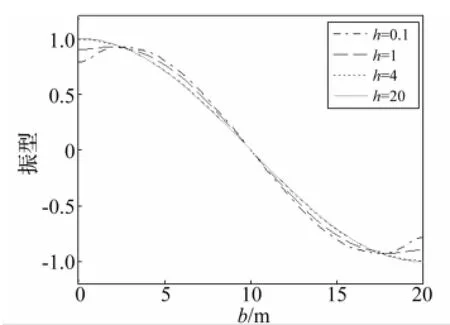
图17 b=20 m时不同h一阶sloshing模态振型Fig.17 Free surface shape for 1st orders sloshingmode for different h

图18 b=20 m时不同h二阶sloshing模态振型Fig.18 Free surface shape for 2nd orders sloshingmode for different h

图19 CFD模型Fig.19 CFD model
宽20 m、不同液面高度时piston模态振型曲线见图16。该图进一步表明,液面越低piston模态在月池宽度方向波峰越大。液面超过12 m时波峰基本消失,月池内流体垂向振动类似于刚体运动。月池宽20 m时不同液面高度对应二阶sloshing模态振型曲线见图17、图18。两图表明,sloshing模态一、二阶振型接近月池两侧壁处出现波峰,随液面升高波峰逐渐降低;液面高于2 m时该波峰基本消失。
2.4 数值仿真对比
利用数值仿真方法计算月池自振并对比与分析,以验证结果的有效性。计算所用CFD软件FLUENT为基于非结构化网格的有限体积法,利用动网格技术模拟边界运动。在其前处理模块Gambit中建立计算模型、划分网格。月池模型为二维模型,包括月池内流体、月池外流体、船体,月池内外流体相联通。月池及两侧船体结构均宽20 m,计算区域总宽160 m。用非结构性三角形单元进行网格划分,对月池内流体网格局部细化,以便对月池内流体运动准确刻画。计算模型见图19。
据sloshing模态一阶自振频率计算一阶周期T1=2π/ω1,对液面高2 m、10 m时模型施加周期T1的水平简谐激励。月池内流体运动响应稳定后取体积分数0.5的自由液面曲线,与一阶振型进行对比。CFD计算液面高2 m曲线与解析解液面高1 m、2 m的一阶sloshing模态振型曲线对比见图20。由图20看出,解析解与CFD具有相同特征。靠近两侧壁处出现峰值。CFD模拟液面高2 m时结果与解析解中液面高1 m的曲线稳合程度更高。在用势流理论求解时设流体为无粘理想流体,而在CFD方法模拟中,流体粘性对侧壁处流体也会产生影响,造成侧壁处波峰较明显。但粘性对计算结果影响相对整体振型尺度较小,可忽略。液面高10 m时CFD计算曲线与解析解一阶sloshing模态振型曲线对比见图21。由图21看出,两条曲线拟合较好。

图20 Sloshing模态解析解与h=2 m时CFD自由液面计算结果对比Fig.20 Free surface shape of analytical solution and CFD solution when h=2 m in sloshingmode
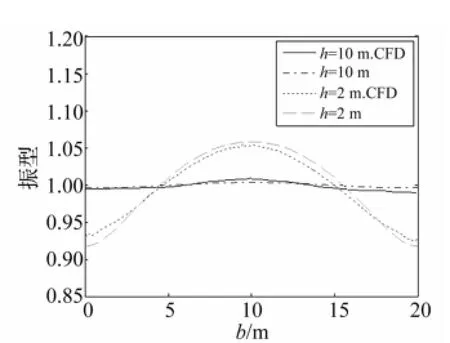
图22 Piston模态解析解与h=10 m时CFD自由液面计算结果对比Fig.22 Free surface shape of analytical solution and CFD solution in pistonmode

图21 Sloshing模态解析解与h=10m时CFD自由液面计算结果对比Fig.21 Free surface shape of analytical solution and CFD solution when h=2m in sloshingmode
据piston模态自振频率计算垂荡周期T0=2π/ω0,对液面高2 m、10 m时模型施加周期T0的垂荡方向简谐激励。月池内流体运动响应稳定后取体积分数0.5的自由液面曲线与piston模态振型进行对比。CFD计算及解析解自由液面对比曲线见图22。由图22看出,CFD结果与解析解结果拟合较好,CFD计算中自由液面在高2 m时出现明显波峰,随液面升高其波峰减小趋于平面,与解析解呈现相同变化趋势。对比图20~图22各曲线可知,利用势流理论研究底部开放月池的振动特性,求解效率高,结果精度能满足要求。
3 结 论
本文利用线性势流理论建立月池计算模型,研究其自振频率及自由液面。对底板完全开放的月池,自振特性显现垂向piston模态及水平方向sloshing模态。结论如下:
(1)月池流体有piston及sloshing两种运动模态,其中piston模态频率低于sloshing模态各阶固有频率,sloshing模态振型的奇数阶为反对称振型,偶数阶为对称振型。
(2)月池液面高度变化对piston模态频率影响较大:液面增度piston模态频率降低,液面足够高时piston模态频率可能接近结构的自振频率及波浪入射频率,引起结构大的振动;月池宽度变化对sloshing模态频率影响较大,b<10时sloshing模态频率下降较明显。
(3)液面高度h较小时sloshing模态振型在接近月池两侧壁处出现波峰,piston模态在月池宽度方向出现波峰。液面增度波峰逐渐降低并消失,此时月池内流体的垂向振动为刚体运动。
(4)CFD结果与半解析解piston模态及sloshing模态振型变化规律相同,显示半解析解计算精度良好。
[1]董艳秋.深海采油平台波浪载荷及响应[M].天津:天津大学出版社,2005.
[2]Drobyshevski Y.Hydrodynamic coefficients of a twodimensional,truncated rectangular floating structure in shallow water[J].Ocean Engineering,2004,31:305-341.
[3]Wei Y,Yang J,Chen G,et al.Experimental study on the hydrodynamic performance of FDPSO and SRV[J].Ships and Offshore Structures,2012,7(4):357-369.
[4]Faltinsen O M,Timokha A.Sloshing[M].London:Cambridge University Press,2009.
[5]Miles JW.On the eigenvalue problem for fluid sloshing in a half-space[J].Journal of Applied Mathematics and Physics,1972,23(6):861-869.
[6]Gupta H,Blevins R,Banon H.Effect of moonpool hydrodynamics on spar heave[C].ASME,2008.
[7]Aalbers A B.The water motions in a moonpool[J].Ocean Engineering,1984,11(6):557-579.
[8]Molin B.On the piston and sloshingmodes inmoonpools[J].Journal of Fluid Mechanics,2001,430(1):27-50.
[9]Faltinsen O M,Rognebakke O F,Timokha A N.Twodimensional resonant piston-like sloshing in a moonpool[J].Journal of Fluid Mechanics,2007,575:359-397.
[10]Kristiansen T,Faltinsen O M.Application of a vortex tracking method to the piston-like behaviour in a semientrained vertical gap[J].Applied Ocean Research,2008,30(1):1-16.
[11]Kristiansen T,Faltinsen O M.A two-dimensional numerical and experimental study of resonant coupled ship and pistonmodemotion[J].Applied Ocean Research,2010,32(2):158-176.
[12]Kristiansen T,Faltinsen O M.Gap resonance analyzed by a new domain-decomposition method combining potential and viscous flow Draft[J].Applied Ocean Research,2012,34:198-208.
[13]姚熊亮,康庄.圆形月池流激振荡实验研究[J].力学学报,2007,39(3):333-342.
YAO Xiong-liang,KANG Zhuang.Experimental research on flow induced oscillation of circle moonpool[J].Chinese Journal of Theoretical and App lied Mechanics,2007,39(3):333-342.
[14]康庄,姚熊亮.浪流条件下月池内流体活塞振荡特性实验研究[J].哈尔滨工程大学学报,2008,29(3):209-216.
KANG Zhuang,YAO Xiong-liang.Experimental research on piston oscillating behavior of fluid in a moonpool with waveflow[J].Journal of Harbin Engineering University,2008,29(3):209-216.
[15]Zhou Hua-wei,Zhang Hong-sheng.Radiation and diffraction analysis of a cylindrical body with amoon pool[J].Journal of Hydrodynamics,Ser.B,2013,25(2):196-204.
[16]Zhang Xin-shu,Bandyk Piotr.On two-dimensionalmoonpool resonance for twin bodies in a two-layer fluid[J].Applied Ocean Research,2013,40:1-13.
[17]翟瑞彩,谢伟松.数值分析[M].天津:天津大学出版社,2000.
Natural vibration characteristics of fluid in a two dimensional rectangular moonpool
HUANG Lei,LIU Li-qin,TANG You-gang
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China)
Based on the linear potential theory,the equations of fluid motions in a two dimensional rectangular moonpoolwere converted into an eigenvalue problem by Galerkin method.Via solving the coefficientmatrix of potential function,the semi-analytical solution of natural frequencies and shapes of fluid was obtained and the influences of geometric parameters of themoonpool on its natural vibration characteristics were discussed.The results show that there exist two natural vibration modes of fluid in themoonpool,namelt,the piston mode and sloshing mode.The piston mode frequency in vertical direction decreases as the liquid height increases and ismainly determined by the liquid height,whereas sloshingmode frequencies decreases as themoonpool width increases and mainly depend on themoonpoolwidth.In the piston mode shape crestappears as the liquid depth is small,and vanishes as the liquid depth increases.The CFD method was used to verify the semi-analytical solution and the free surface curves in the two results are in good coincidence.
moonpool;semi-analytical solution;natural vibration characteristics;potential theory
P751
:A
10.13465/j.cnki.jvs.2014.22.025
国家自然科学基金资助项目(51179125)
2013-05-15 修改稿收到日期:2013-11-21
黄磊男,博士生,1981年生
刘利琴女,博士,副教授,1977年生

