外激励作用下输流管道伴随内共振的非线性振动分析
梁 峰,包日东,金 莹,苏 勇
(沈阳化工大学能源与动力工程学院,沈阳 110142)
外激励作用下输流管道伴随内共振的非线性振动分析
梁 峰,包日东,金 莹,苏 勇
(沈阳化工大学能源与动力工程学院,沈阳 110142)
利用多元L-P法研究外部周期激励下两端固定输流管道伴随内共振的非线性受迫振动问题。外激励流固耦合系统固有频率第二阶约为第一阶3倍且激励频率接近前两阶固有频率中间值时会发生伴随强烈内部共振的组合共振,并用多元L-P法求解振动响应,分析前两模态运动及外激励幅值对内共振的影响。数值算例揭示出系统因内共振发生的更丰富、复杂的动力学行为,随激励幅值增大内共振发生趋势降低,响应形式亦发生变化。用多元L-P法研究非线性动力学便捷、高效。
输流管道;非线性振动;内共振;外周期激励;多元L-P法
输流管道广泛应用于航空航天、水利工程、石油工业、农业及日常生活中,其振动稳定性问题一直被关注。(作为典型流固耦合系统,输流管道振动失稳通常由与内部流体耦合所致。对此,利用理论、实验方法进行的研究发现包括颤振、屈曲、参数共振、分岔及混沌等多种动力学现象[1-3]。诸多工程结构中输流管道不仅受内流作用亦常受外部激励作用,如横向风载、地震载荷及支承运动时产生的激励(该载荷通过适当变换可简化为周期载荷)等,虽激励幅值较小,但系统频率关系满足某些条件,如第二阶固有频率接近第一阶的3倍,此时管道系统则会发生强烈内部共振。关于动力学系统内共振问题,Wang等[4-7]分别利用悬索、梁、板及壳模型进行研究,表明内共振不仅存在,且其对系统非线性动力学行为影响明显。Xu等[8-9]理论上解释内流引起管道内共振机理。Panda等[10-11]用多尺度法研究脉动内流引起具有内共振的主参数共振及组合参数共振,认为出现内共振,系统动力学行为更复杂。以上研究均未考虑外部激励。而海洋立管、海底管道、桥梁悬跨管道等,对风、流引起的横向振动尤其涡激振动[12-13]、端部激励引起的参数激励振动、考虑内流及外部激励管道的非线性振动研究均取得较多成果。本文对内流、外部周期激励联合作用管道出现内共振的非线性动力学行为进行深入研究。
组合共振为工业管道常发生但得不到重视的非线性振动。由于发生条件较苛刻,且其振动形态较复杂,对其研究较少。事实上,其振动危害并不亚于主共振及其它类共振。尤其伴随内共振发生时其振幅较大、振型较复杂,为管道振动疲劳破裂的重要原因之一。Panda等[11,14-15]曾对输流管道组合共振进行研究,分别利用平均法、数值仿真技术研究脉动流管道组合参数共振稳定性及响应,认为在组合共振区域内亦会发生准周期、组合周期等多种运动,并证明组合共振的复杂性。以上研究只考虑内流激励,本文在此基础上增加外部激励,重点研究和式组合共振(激励频率约为前两阶固有频率和的一半)响应问题。本文研究所用多元L-P法已广泛用于非线性系统的动力学特性分析。如Lau等[16-17]利用该法分析动力学系统非线性振动问题;Yang等[18]用改进的L-P法(MLP)研究参数激励下强非线性Van der Pol-Duffing型振荡器主共振响应;Pušenjak[19]用拓展的L-P法(ELP)分析具有三次非线性的动力学系统非稳态振动。本文用该方法对外部周期激励下两端固定输流管道伴随内共振的组合共振响应进行研究,获得幅-频响应曲线,并利用增量谐波平衡法进行验证,分析该振动的响应特性,讨论外激励幅值对内共振的影响。
1 力学模型及控制方程
图1为外部简谐激励下两端固定输流管道力学模型。实际上无论外部周期力或支承简谐运动,经一定变换后均可简化为简谐激励。
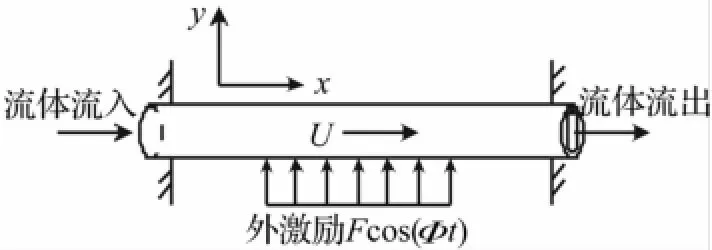
图1 外部激励下输流管道模型Fig.1 Model of a fluid-conveying pipe under external excitation
设管道轴线为x轴,管道只发生横向面内振动y(x,t),U为管内定常流速,F为外激励单位长度幅值,Φ为频率。管道单元、流体单元受力可用牛顿法推导出其横向振动控制方程[15]为

式中:EI,A1,N,L,m分别为管道弯曲刚度、管壁横截面积、预紧力、长度及单位长度质量;M,A分别为管内流体单位长度质量及通流截面积。

式中:( )′,(·)分别表示∂( )/∂ξ及∂( )/∂τ。
由式(3)及研究结果[15,20-21]知,用2阶Galerkin法离散管道系统精度已足够。本文取
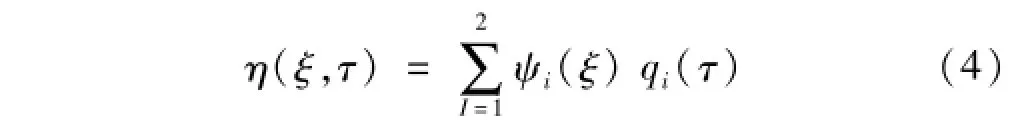
式中:ψi(ξ),qi(τ)(i=1,2)为两端固定梁前两阶特征函数及广义坐标。
输流管道为细长结构,其外部激励通常非同相位(因激励幅值较小,忽略非同相位激励引起的波长效应),本文考虑二维激振力、模态cosφ及sinφ正交,故其相位差为π/2;设激励幅值列阵,外部激励F cos(Φt)通过式(2)无量纲后为[f1cosφ,f2sinφ]T,将式(4)代入式(3),用振型正交性可得二元二阶常微分方程组为

2 用多元L-P法求解
为用多元L-P摄动法,令式(5)引入摄动小参数ε,变为
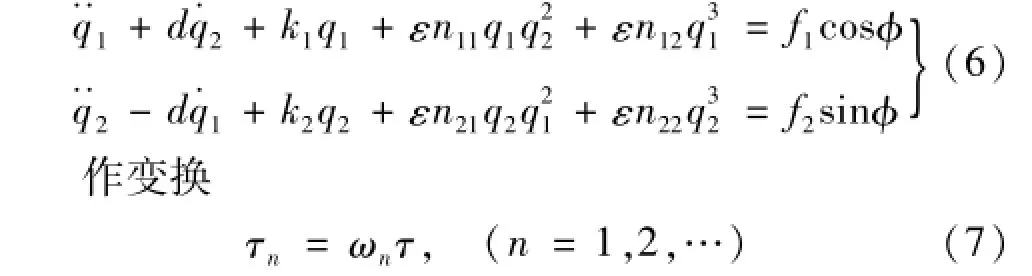
式中:ωn为独立非线性响应频率;τn为多个不同时间变量。则qn由单个时间变量τ的函数变为多个独立时间变量τn的函数(本文n=2)。将qn(τ1,τ2,ε)与ωn(ε)展开为ε的幂级数为
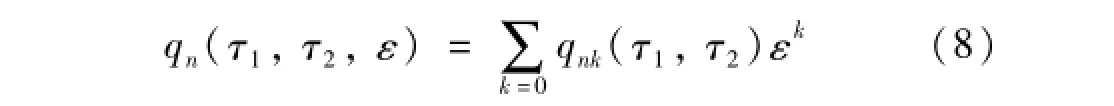
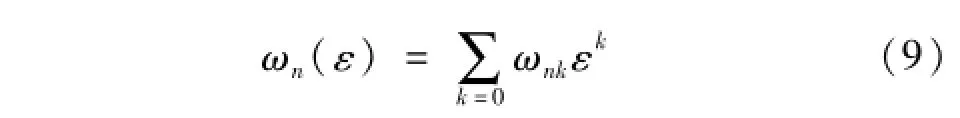
式中:ω10,ω20为系统前两阶固有频率;ωnk(k=1,2,…)为待定参数。
qn对无量纲时间变量τ的一、二阶导数为

由式(12)得q10,q20代入式(13),消去长期项获得可解性条件,从而获得外激励频率与响应振幅之关系。
考虑外激励频率Ω在前两固有频率中间值附近及内共振,有

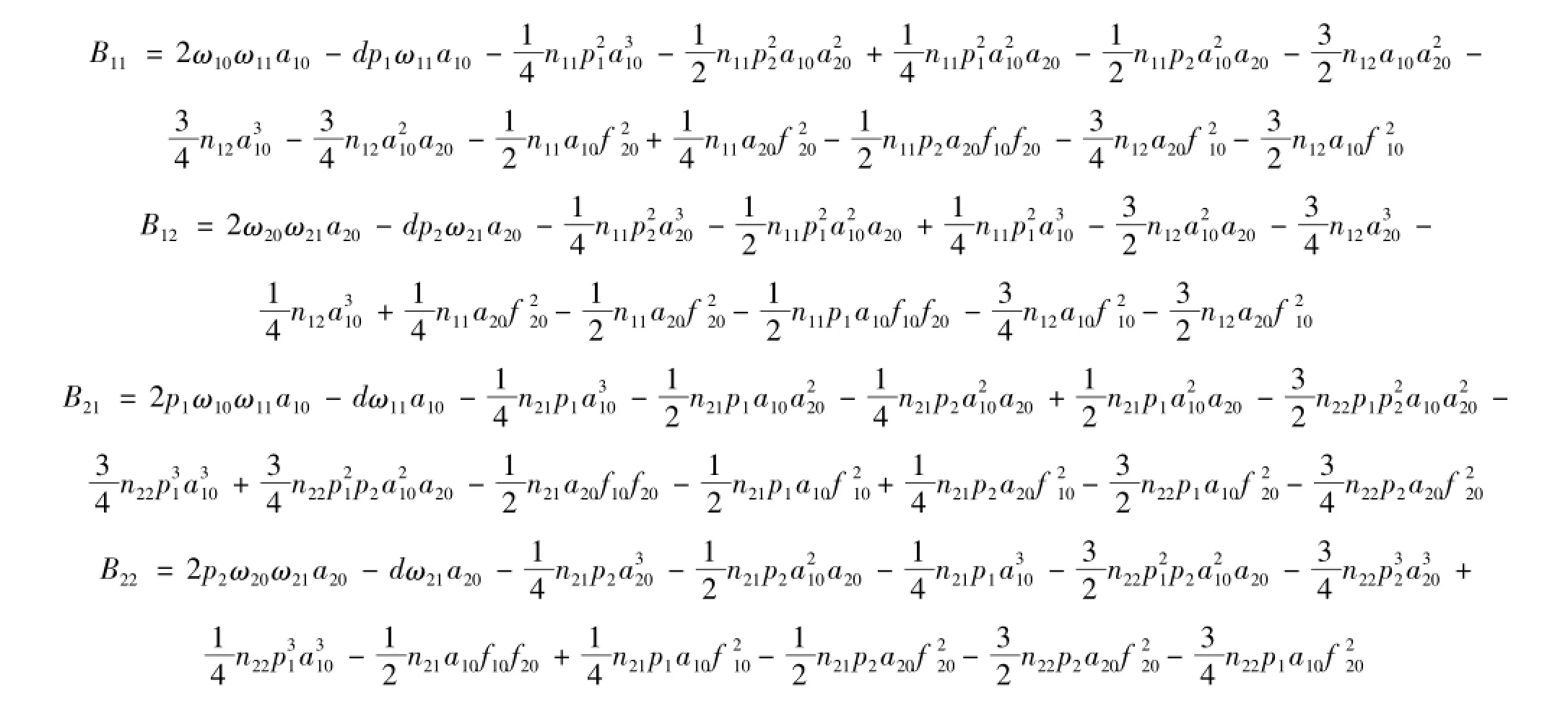
为消去长期项,应使B11,B12,B21,B22全部为零,但由此所得方程组会因不相容无法求解。因此设q11,q21特解为
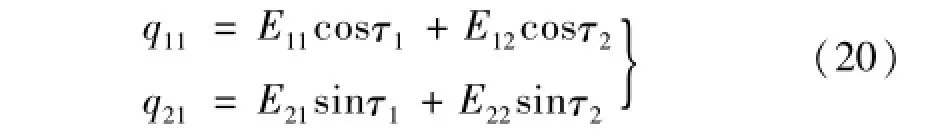
将式(20)代入式(19),比较cosτ1,cosτ2,sinτ1,sinτ2各项系数,可得以E11,E12,E21,E22为未知量的方程组,其非零解条件为
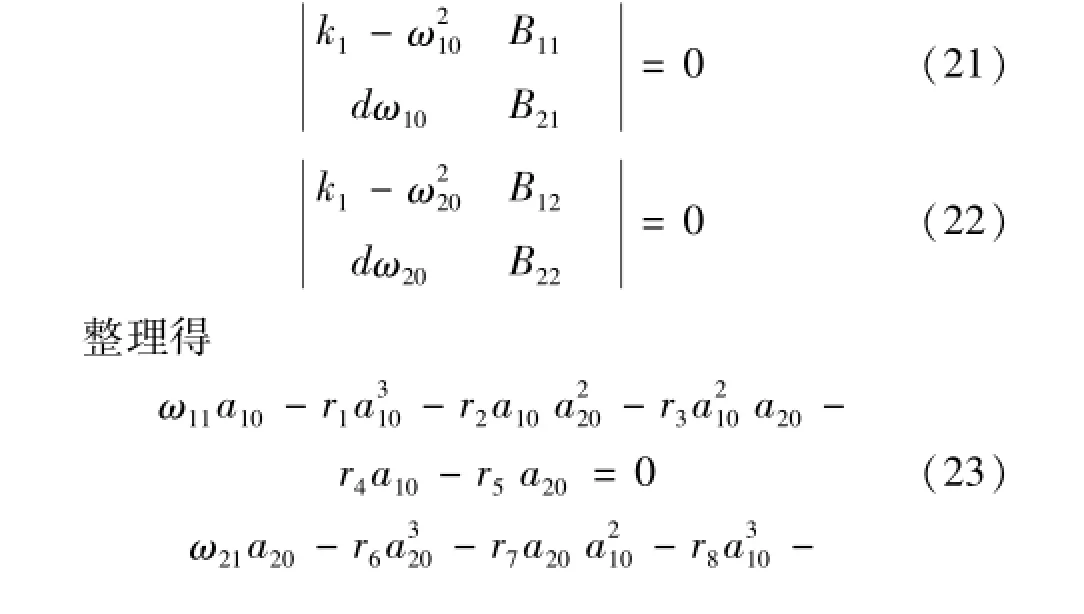

判别式值可出现几种根,即①若Δ>0,有1个实根与1对共轭虚根;②Δ=0,且P=Q=0,有3个零根;③Δ=0,且P≠0,Q≠0,有3个实根,其中两个相等;④Δ<0,有3个不等实根。可由实根个数分析系统的内共振。
3 IHB法验证
为验证多元L-P法的有效性,本文用半解析、半数值法-增量谐波平衡法(Incremental Harmonic Balancemethod,IHB法)重新求解管道系统受迫振动响应。IHB法由Lau等[22]提出,并在具有三次非线性及陀螺特性等强非线性系统中广泛应用。该法将数值分析中的增量法与传统谐波平衡法有机结合,且对所研究系统非线性的强、弱无限制,为研究非线性振动尤其强非线性振动的有效方法。梁峰等[3]曾利用IHB法研究输流管道系统参数共振响应,获得精确结果。此处用该方法对多元L-P法结果进行验证。限于篇幅,略去求解过程。
4 算例分析
结合数值算例分析输流管道含内共振组合共振响应。算例参数[14-15]为Mr=0.447,T=15,u=4.75,γ=5 000。求得管道系统固有频率及它系统参数值为

由于ω20≈3ω10,系统可能会发生内共振。由式(28)、(29)可得P,Q均为a10,f1,f2的复杂函数。由判别式(30)看出?acr或a10<-acr时有Δ>0,式(27)仅1个实根,即对给定的a10值,仅1个外激励频率Ω值与其对应;当时有Δ<0,式(27)有3个不等实根,对给定的a10值,有3个外激励频率Ω值与其对应,系统会发生强烈内共振。acr为f1,f2的复杂函数,f1,f2越大acr值越小。取f1=f2=0.4进行分析,求得f10=-3.967 39×10-4,f20=9.356 74×10-5。而据p1,p2,f10,f20值,对式(23)、(24)数值求解比较式(16)中各谐波项幅值知,系统响应主要发生于q1的cosτ1项及q2的sinτ2项,故只分析a10及p2a20两项幅值。
f1=f2=0.4时a10及p2a20随激励频率Ω变化见图2。由图2看出,响应曲线中出现环状,即在一定幅值范围内1个振幅值对应3个频率值,说明系统已发生内共振;各模态响应图上、下两半平面基本对称,表明均已发生内共振;a10,a20均有两个解,每个解横跨上、下两半平面;振动响应只发生在Ω>2ω10即外激励频率大于2倍的第一阶固有频率区域;外激励幅值较小时在Ω≈2ω10(Ω>2ω10)区域附近a10及a20呈明显内部共振特征,两模态相互激励,大小相互转换。说明出现内共振过程中两模态间已进行能量交换。图2中利用IHB法求解响应结果验证多元L-P法结果并对比知,二者响应振幅较小时较吻合,但随振幅增大二者差别逐渐增大。原因为多元L-P法为摄动法,仅适合求解弱非线性振动问题,而IHB法为半解析半数值方法,对强、弱非线性振动均适用,故二者在小振幅时能吻合,振幅增大时多元L-P法结果误差亦增大。
图3、图4为改变激励幅值后两模态响应曲线。由图3看出,f1=f2=2时a10及p2a20曲线中环状部分(发生内共振区域)明显减小;由图4看出,f1=f2=4时两模态内共振已完全消失。说明随激励幅值增大acr值减小,系统内共振发生趋势降低。激励幅值大于某个临界值后内共振不再发生。响应曲线形态也会随激励幅值增大发生变化,均体现伴随内共振的组合共振响应特点。

图2 f1=f2=0.4时幅-频响应曲线Fig.2 Frequency-amplitude curves for f1=f2=0.4

图3 f1=f2=2时幅-频响应曲线Fig.3 Frequency-amplitude curves for f1=f2=2
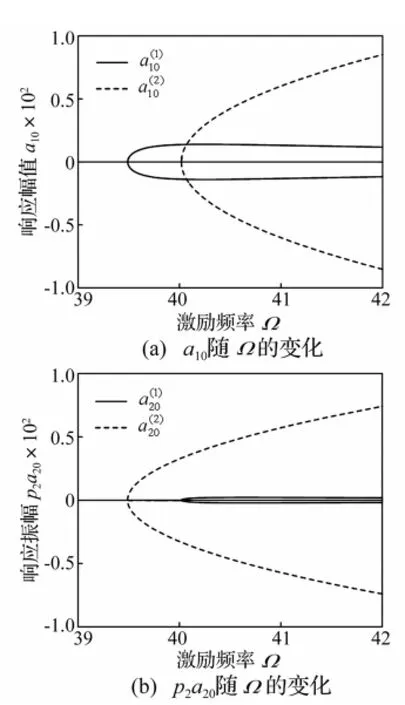
图4 f1=f2=4时幅-频响应曲线Fig.4 Frequency-amp litude curves for f1=f2=4
由式(23)、(24)知,外激励幅值f1,f2不都为零,则响应振幅a10不为零,a20只在某一激励频率Ω=Ω1处可能为零。Ω1可由式(23)、(24)令a20=0求得,亦为f1,f2的函数。第1模态a10的频率为Ω/2,其振动为次谐波振动,存在于整个频率域;第2模态a20的频率为3Ω/2,其振动为超次谐波振动,存在于除Ω1的频率域;在Ω=Ω1处是否存在尚需额外条件判断;第3模态f10的频率为Ω,其振动为恒定振幅的基谐波振动,存在于整个频率域。系统实际响应为3种振动的叠加。
5 结 论
本文用多元L-P法并结合数值算例对外激励作用下两端固定输流管道伴随内共振组合共振响应进行研究、分析,结论如下:
(1)对外部周期激励的两端固定输流管道,当系统第二阶固有频率约为第一阶的3倍且激励频率接近前两阶固有频率中间值时,系统会发生含强烈内部共振的组合共振。此时前两阶模态相互激励,振幅相互交换,致系统非线性动力学行为更丰富、复杂。
(2)外激励幅值为影响内共振的关键因素。随激励幅值增大内共振发生趋势降低,响应形态亦发生变化。激励幅值超过某临界值后内共振完全消失。管道系统受迫振动响应通常由基谐波、次谐波及超次谐波振动叠加产生。
(3)利用增量谐波平衡法对多元L-P法结果验证发现,二者结果在小响应振幅时吻合较好,表明多元L-P法在分析多模态动力学系统(弱)非线性振动问题的有效性。
[1]Ni Q,Zhang Z L,Wang L.Application of the differential transformationmethod to vibration analysis of pipes conveying fluid[J].Applied Mathematics and Computation,2011,217(16):7028-7038.
[2]Wang L,Dai H L,Qian Q.Dynamics of simply supported fluid-conveying pipes with geometric imperfections[J].Journal of Fluids and Structures,2012,29:97-106.
[3]梁峰,杨晓东,闻邦椿.脉动流激励下输流管道的参数共振IHB方法研究[J].振动与冲击,2008,27(9):44-46.
LIANG Feng,YANG Xiao-dong,WEN Bang-chun.Analysis of parametric resonances of pipes conveying pulsating fluid by IHB method[J].Journal of Vibration and Shock,2008,27(9):44-46.
[4]Wang L H,Zhao Y Y.Nonlinear interactions and chaotic dynamics of suspended cables with three-to-one internal resonances[J].International Journal of Solids and Structures,2006,43(25/26):7800-7819.
[5]Dwivedy SK,Kar R C.Simultaneous combination and 1:3:5 internal resonances in a parametrically excited beam-mass system[J].International Journal of Nonlinear Mechanics,2003,38(4):585-596.
[6]Ribeiro P,Petyt M.Non-linear free vibration of isotropic plates with internal resonance[J].International Journal of Nonlinear Mechanics,2000,35(2):263-278.
[7]Thomas O,TouzéC,Chaigne A.Non-linear vibrations offree-edge thin spherical shells:modal interaction rules and 1:1:2 internal resonance[J].International Journal of Solids and Structures,2005,42(11/12):3339-3373.
[8]Xu J,Yang Q B.Flow-induced internal resonances and mode exchange in horizontal cantilevered pipe conveying fluid(I)[J].Applied Mathematics and Mechanics(English Edition),2006,27(7):935-941.
[9]Xu J,Yang Q B.Flow-induced internal resonances and mode exchange in horizontal cantilevered pipe conveying fluid(II)[J].Applied Mathematics and Mechanics(English Edition),2006,27(7):943-951.
[10]Panda LN,Kar R C.Nonlinear dynamics of a pipe conveying pulsating fluid with parametric and internal resonances[J].Nonlinear Dynamics,2007,49(1/2):9-30.
[11]Panda LN,Kar R C.Nonlinear dynamics of a pipe conveying pulsating fluid with combination,principal parametric and internal resonances[J].Journal of Sound and Vibration,2008,309(3/5):375-406.
[12]Dai H L,Wang L,Qian Q,et al.Vortex-induced vibrations of pipes conveying fluid in the subcritical and supercritical regimes[J].Journal of Fluids and Structures,2013,39:322-334.
[13]Dai H L,Wang L.Vortex-induced vibration of pipes conveying fluid using the method of multiple scales[J].Theoretical and App lied Mechanics Letters,2012,2(2):022006.
[14]Namachchivaya N S,Tien W M.Non-linear dynamics of supported pipe conveying pulsating fluid.2.combination resonance[J].International Journal of Nonlinear Mechanics,1989,24(3):197-208.
[15]Jin JD,Song Z Y.Parametric resonances of supported pipes conveying pulsating fluid[J].Journal of Fluids and Structures,2005,20(6):763-783.
[16]Lau SL,Cheung Y K,Chen SH.An alternative perturbation procedure of multiple scale for nonlinear dynamics systems[J].ASME Journal of Applied Mechanics,1989,56(3):667-675.
[17]Chen SH,Cheung Y K,Lau SL.On the internal resonance of multi-degree-of-freedom systems with cubic nonlinearity[J].Journal of Sound and Vibration,1989,128(1):13-24.
[18]Yang X L,Xu W,Sun Z K,et al.Responses of strongly non-linear oscillator parametrically excited by random narrowband noise[J].Applied Mathematics and Computation,2005,171(2):885-899.
[19]Pušenjak R R.Extended Lindstedt Poincar method for nonstationary resonances of dynamical systems with cubic nonlinearities[J].Journal of Sound and Vibration,2008,314(1/2):194-216.
[20]Païdoussis MP,Issid N T.Dynamic stability of pipes conveying fluid[J].Journal of Sound and Vibration,1974,33(3):267-294.
[21]Païdoussis MP,Issid N T.Experiments on parametric resonance of pipes containing pulsatile flow[J].ASME Journal of Applied Mechanics,1976,43(2):198-202.
[22]Lau S L,Cheung Y K.Amplitude incremental variational principle for non-linear vibration of elastic systems[J].ASME Journal of Applied Mechanics,1981,48(4):959-964.
Nonlinear vibration of a fluid-conveying pipe under external excitation accom panied with internal resonance
LIANG Feng,BAO Ri-dong,JIN Ying,SU Yong
(School of Energy and Power Engineering,Shenyang University of Chemical Technology,Shenyang 110142,China)
An external periodic load was considered to act on a fluid-conveying pipe clamped at both ends,and the nonlinear forced vibration of such a system was explored by the multidimensional Lindstedt-Poincaré(MDLP)method.According to the analysis,when the second natural frequency of the system is nearly thrice the firstone,and the excitation frequency is nearly at the middle of first two natural frequencies,accompanied internal resonance may occur to form a combination resonance.The characteristics of the response were discussed,and the motions of first two modes were investigated in detail.The influence of excitation amplitude on the internal resonance was analyzed.Some numerical examples reveal the rich and complex dynamic behaviors caused by internal resonance and show that the occurrence tendency of internal resonance will die down and the responsemodeswill vary with the increase of excitation amplitude.The convenience and efficiency of the MDLPmethod in predicting nonlinear dynamics are demonstrated by the results of the study.
fluid-conveying pipe;nonlinear vibration;internal resonance;external periodic excitation;multidimensional Lindstedt-Poincarémethod
O326
:A
10.13465/j.cnki.jvs.2014.22.026
国家自然科学基金(51275315);辽宁省教育厅科研项目(L2013160)
2013-08-08 修改稿收到日期:2013-12-04
梁峰男,博士,讲师,1979年8月生

