旱灾对粮食生产影响的非线性动态效应评估

储小俊，曹 杰

(南京信息工程大学，南京 210044)

一、引 言

粮食的稳定生产是保证国家粮食安全的关键。中国是世界上人口最多的国家，以占全球7%的耕地面积养活世界22%的人口，保证粮食的稳定生产一直是关系着我国国计民生的首要任务。但是，我国也是世界上受气象灾害影响最为严重的国家之一，气象灾害导致的损失占所有自然灾害总损失的70%以上。在全球气候持续变暖的大背景下，各类极端天气气候事件发生得更加频繁，气象灾害造成的损失和影响不断加重。我国是一个农业大国，农业在国民经济中居于基础性地位，而农业在三大产业中现代化程度最低，农民收入较低，抗风险能力较弱。因此，气象灾害严重影响农民的收入、农业的发展以及我国的粮食安全。

基于此，学者们普遍重视自然灾害对粮食产量影响问题的研究。李茂松等根据建国后近50年的粮食产量统计资料，分析了各个年代主要粮食作物产量与各影响因素之间的关系，结果表明:自然灾害对我国粮食产量的影响极大。［1］王春乙等认为干旱、洪涝和冰冻是影响作物产量的主要气象灾害，而旱灾又是最严重的灾害。［2］龙方等采用灰色关联分析法进行实证研究，结果表明，在稻谷单产变化中，自然灾害影响产量与其他灾害成灾率的关联度最大。［3］卢丽萍等采用统计分析方法进行研究，发现粮食产量与受灾程度出现周期性波动，受灾程度与相应年份的产量负相关。［4］You等基于生产函数模型研究了1979年—2000年间中国小麦产量与气候变化之间的线性关系，得出气温每升高1℃，中国小麦总产量将减少1.5%—5.4%的结论。［5］Lin等的研究表明:温度、降水和平均日照时数变化对小麦产量变化的弹性分别为 －0.76、0.66和 －0.38，对水稻产量变化的弹性分别为 －2.61、－1.72和0.59，对玉米产量变化的弹性分别为3.14、1.64和－0.60。［6］崔静等运用超越对数生产函数模型分析了1975年—2008年作物生长期气候变化(温度、降水和日照时数)对中国主要粮食作物单产的影响。研究表明:总体而言作物生长期内气温升高对粮食单产具有负面影响，但对不同品种、不同地区粮食单产的影响具有差异性;降水量的增加对粮食单产的影响因粮食品种而异;日照增加主要通过与地区的交互作用影响粮食单产。［7］

上述有关自然灾害对粮食生产影响的研究已经取得了值得肯定和借鉴的成果，但仍然存在可以继续拓展和改善的空间，主要表现在两个方面:一是现有研究多隐含着假定天气变量和粮食产量存在线性关系这一前提，二是假定产量对天气变量的依赖关系保持不变。但实际上，这两种假定过于严格。因为首先线性相关不能代表所有的相关关系;其次，线性相关是一种全局相关系数，从防灾减灾的角度看，人们更关注尾部相关性①尾部相关性是指在极端情况下的相依性，可以分为上尾相关和下尾相关。上尾相关是指粮食高产量与自然灾害之间的关系，下尾相关是指粮食低产量与严重的自然灾害之间的关系。而非全局相关性;最后，在外部环境发生变化的情况下，如灌溉技术的提高、作物新品种抗旱能力的提高等，都会影响天气对产量的作用——过去可能导致减产的天气，现在或将来未必会导致减产，也就是说，天气和产量的关系也是动态变化的。

Copula函数方法特别强调尾部相关性，可以很好地捕捉变量之间的非线性关系，因此，在金融领域已经被广泛应用，在农业经济领域也逐步开始使用。例如，Bokusheva使用 Copula函数研究了产量和天气指数变量的联合分布。［8］谢凤杰等运用 Copula方法估算玉米、小麦与大豆三种农产品单产及价格的联合概率密度，并在此基础上采用模拟法测算了三种农产品的收入保险费率。［9］但是目前还没有文献利用Copula函数方法研究气象灾害和粮食产量之间的关系。作为一种有效研究变量间相互关系的方法，使用Copula函数方法至少有以下三个优点:一是反映非线性关系，二是突出尾部相关性，三是可以利用时变Copula函数反映气象灾害和粮食产量之间的动态关系。

二、数据与方法

(一)数据来源与处理

本文涉及的数据主要来源于《中国农村统计年鉴》和《新中国五十年农业统计资料》，样本区间为1950年至2011年(缺少1968年、1969年的受灾数据，因此样本中不包括这两年)。根据前人研究的成果可知，干旱是威胁粮食安全最主要的气象灾害，受灾面积最大，因此，本文的研究以旱灾为例。由于在统计年鉴中没有单列不同作物品种的受灾情况，因而参照龙方等的方法，假定各品种受灾状况等同于总的受灾比率。旱灾比率定义如下:

因为多数Copula函数描述的是变量间的正相关关系，所以定义变量Z表示未受旱灾比率:

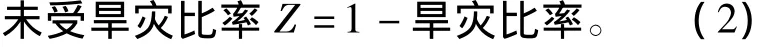
粮食作物品种以水稻、小麦和玉米为例，产量使用单产数据。随着时间的推移，作物品种不断改良，农用化肥效力以及种植技术不断提高，作物的趋势产量在逐年增加。因此，使用多项式拟合的方法计算趋势产量，进行去趋势化处理，并转化成以2011年为基期的产量:

式中，t=1950，……，2011;Y't表示以 2011 年为基期、去趋势后的产量;Yt表示原始产量序列;^Yt表示第t年的趋势产量。

(二)Copula函数及其估计

根据Sklar定理，边缘分布为连续分布的二元分布函数可以写为:

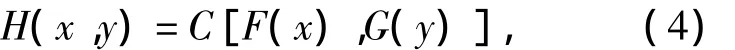
其中，F(x)、G(y)是边缘分布函数，C就是H的Copula，而且C也是边缘分布为(0，1)上均匀分布的联合分布函数。Joe Harry提出如下Copula函数(简称 JC － Copula)［10］:

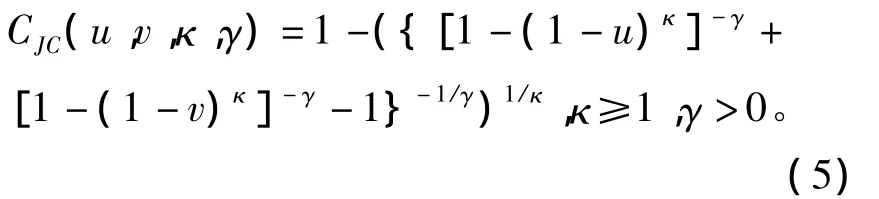
JC－Copula函数的优点在于可以同时捕捉上下尾相依性结构，其参数与尾部相关系数有一一对应的关系:

但JC－Copula也存在一个不足，即使尾部相关系数相等，JC－Copula仍然表现为非对称性，因此，Patton Andrew J.提出对称的 JC－Copula(SJC－ Copula)［11］:

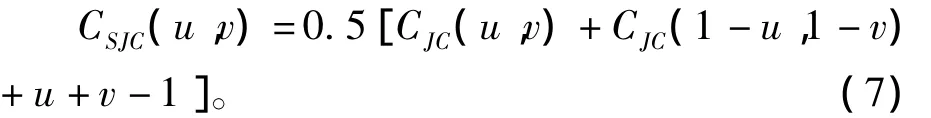
SJC－Copula能同时捕捉上下尾相依性，因此得到了广泛的应用。

变量之间的相关关系不仅是非线性的，还可能随着内外部环境的变化而发生波动。例如，农业技术进步等因素也会影响到天气与产量的关系，因此需要建立一种动态的非线性模型来描述变量之间的这种非线性动态相依结构关系。

Patton提出，可以用一个类似于ARMA(1，10)的过程来定义Copula函数参数的时变性。在每一个时间点上，时变的上尾或下尾的具体表达式为:

其中β值表明尾部相关系数与其自身滞后一期的相关性。函数Λ(·)为logistic转换函数，定义为，它的作用是为了保证上下尾相关系数在任意时刻都处于(0，1)区间内。阶数q一般取10。

三、实证分析

(一)描述性统计

表1给出了研究样本的变量统计性描述结果。水稻的单产平均数、最大值、最小值分别为4 471.9千克/公顷、6 687千克/公顷、2 017千克/公顷，小麦的单产平均数、最大值、最小值分别为2 423.4千克/公顷、4 837千克/公顷、557千克/公顷，玉米的单产平均数、最大值、最小值分别为3 245.28千克/公顷、5 747千克/公顷、1 073千克/公顷。旱灾的受灾率平均值为14.49%，最大值为26.76%，最小为0.83%。

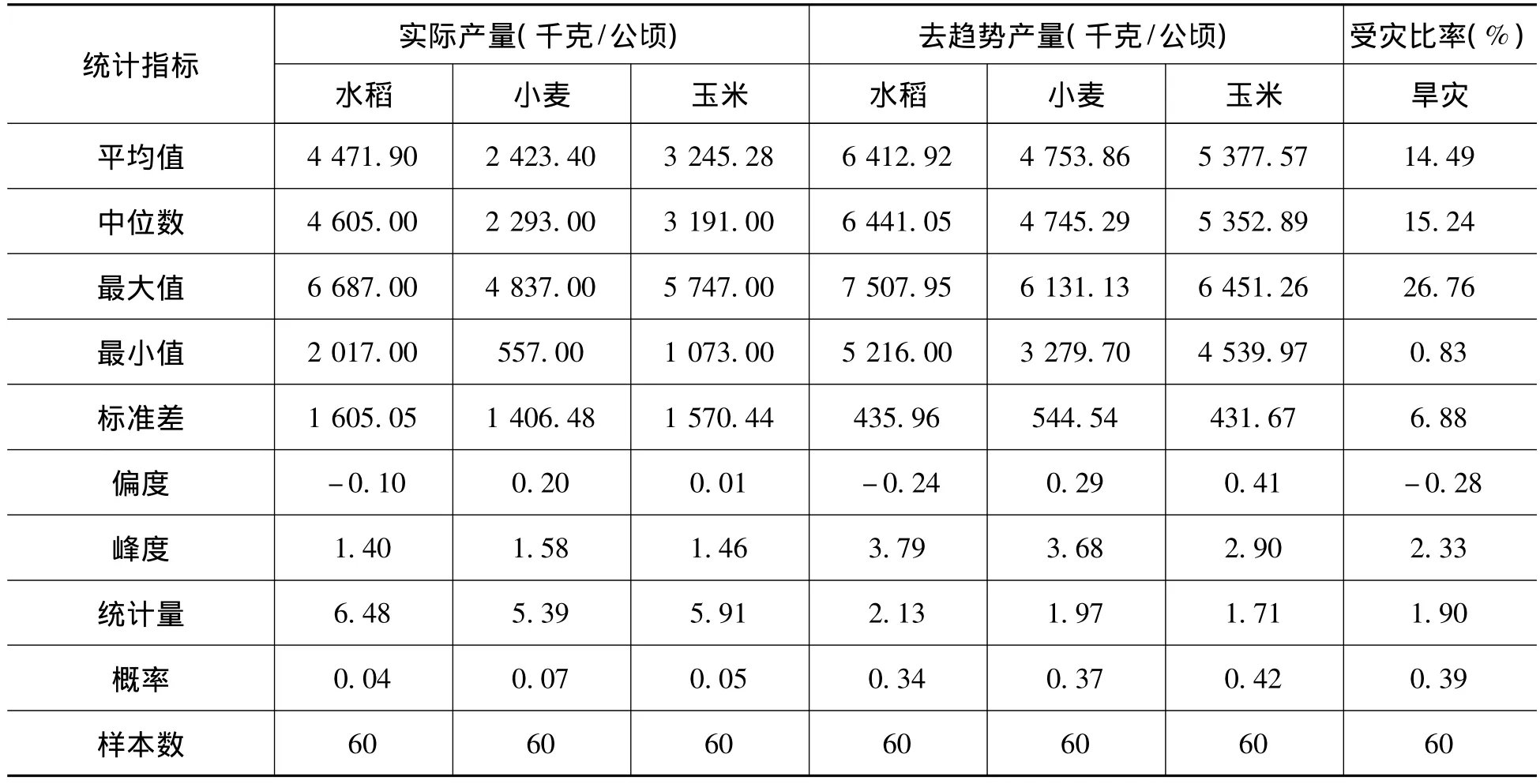
表1 变量的统计性描述

(二)边缘分布的确定

由表1可知，虽然实际产量序列不服从正态分布，但根据公式(3)计算得到的以2011年为基期去趋势后的产量序列和旱灾比率，可以认为服从正态分布。因此，本文选取正态分布拟合去趋势产量和旱灾受灾率序列。边缘分布参数通过MATLAB软件、极大似然估计方法得到。

指定的边缘分布模型能否很好地拟合变量的实际分布，对Copula函数正确地描述变量间的相关结构至关重要，因此要建立评价边缘分布拟合优度的方法。［12］本文参照Diebold F.X等基于序列概率积分变换的密度分布模型的方法，［13］对边缘分布拟合做出评价，即首先对原序列做概率积分变换，然后通过变换后的序列是否服从i.i.d(0，1)均匀分布来检验。

表2中的Kolmogorov－Smirnov统计量及其概率值是根据估计得到的边缘分布，对原序列做概率积分变换，再运用Kolmogorov－Smirnov检验方法，检验变换后的序列是否服从(0，1)均匀分布得到的。表中的Kolmogorov－Smirnov统计量及其概率值表明，对各序列均没有充分的理由拒绝零假设“变换后的序列服从(0，1)均匀分布”。另外，对变换后的各序列做自相关检验还发现，变换后的各序列均不存在自相关，因此可以认为变换后的序列均是独立的。Kolmogorov－Smirnov统计量和自相关检验表明，根据上述模型估计得到的边缘分布，对原序列做概率积分变换后得到的序列均服从 i.i.d(0，1)均匀分布，说明正态模型可以较好地拟合各序列的边缘分布，用它们来描述去趋势产量和受灾序列的边缘分布是合适的。

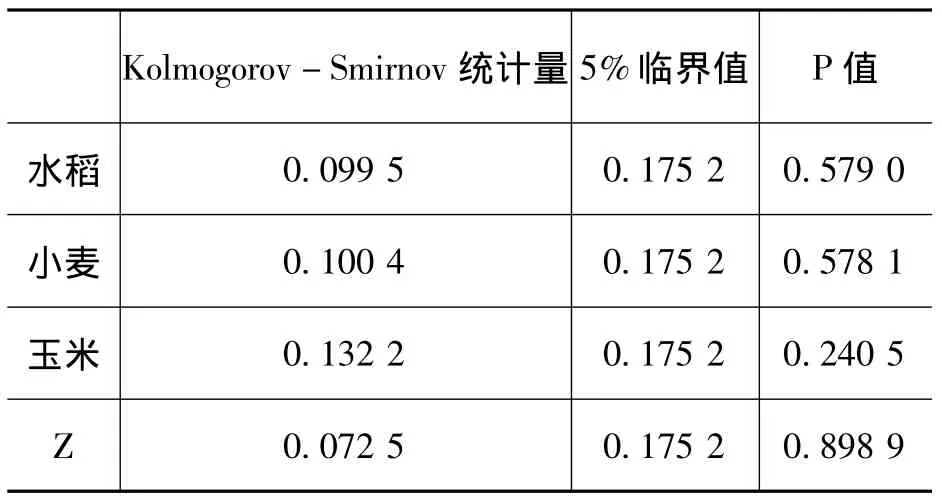
表2 Kolmogorov－Smirnov检验结果

(三)Copula参数估计结果

为了进行比较分析，本文也同时采用静态SJC－Copula进行估计。静态和动态这两种估计结果均列于表3。

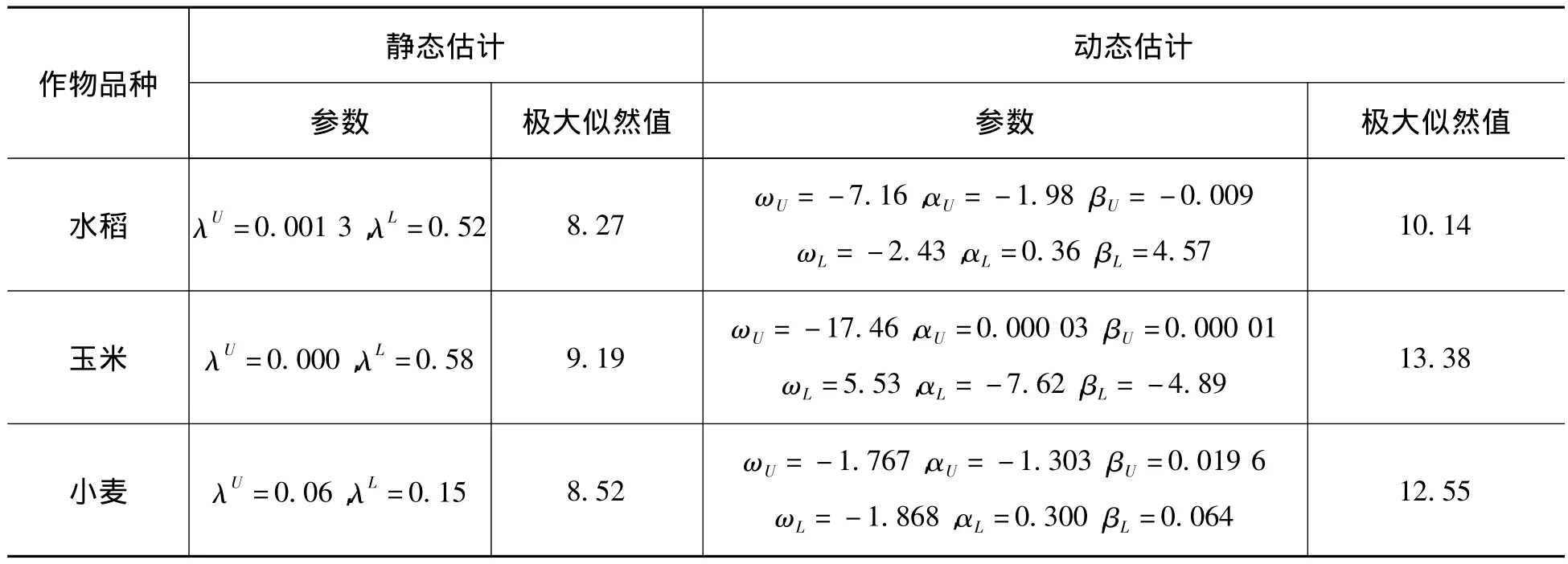
表3 Copula参数估计结果

表3的静态SJC－Copula估计结果显示，无论水稻、玉米还是小麦，与变量Z的下尾相关性均很高，分别为0.52、0.58和0.15，但上尾相关系数分别为0.001 3、0和0.06。这说明，粮食单产与旱灾的关联性表现出非对称性，粮食生产的低产量显著受到旱灾的影响，但是旱灾的减轻并不必然导致粮食的高产。因此，利用传统的全局线性相关系数来度量二者之间的关系并不合适。从β值来看，水稻的 βL为4.57、小麦的 βL为0.064，均大于0，这意味着下尾相关系数存在正自相关，但是玉米的βL为－4.89，小于0，则意味着下尾相关系数存在负相关性。

表3的结果还显示，无论是水稻、玉米还是小麦，动态估计的极大似然值均大于静态值，因此，相对于静态估计方法，动态模型拟合效果更有优势。

在农业灾害风险管理中，人们最为关心的是极端天气条件对农业生产造成的不利影响，且因为水稻、玉米和未受旱灾比率的上尾相关性近乎为0，所以为了简洁起见，本文略去了上尾相关系数图。水稻、玉米和小麦与变量未受旱灾比率Z的动态下尾关系如图1、图2、图3所示。

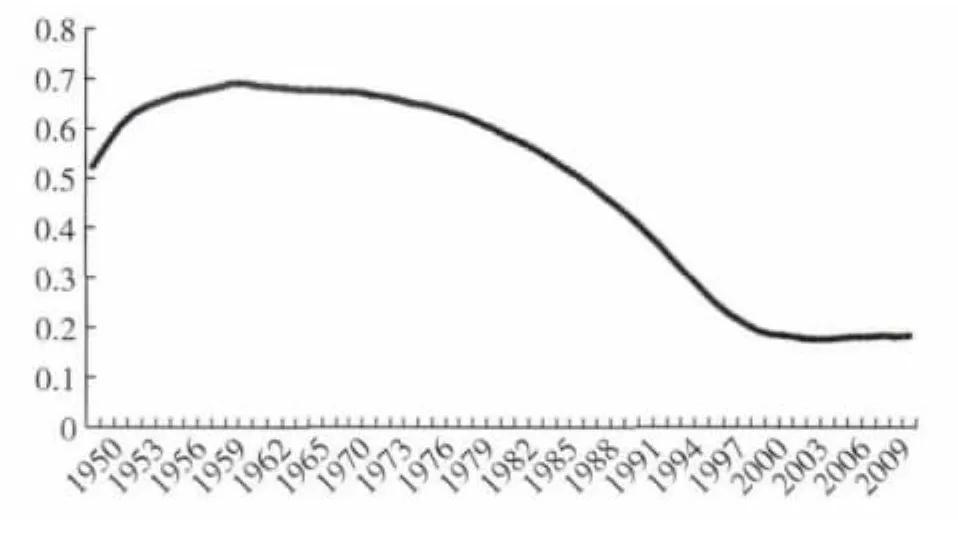
图1 水稻和未受旱灾比率Z的动态下尾相关系数

从图1的动态下尾相关系数中可以看出，水稻受旱灾的影响存在明显的时变性。1950年至1960年，呈递增趋势，相关系数由0.52增加到0.69;从1961年至2000年呈逐渐下降趋势，且下降幅度较大，相关系数在2000年降至0.2;2000年后，二者的相关性几乎保持不变，没有表现出继续下降的态势。这意味着，随着时间的推移，水稻生产技术有所提高，在一定程度上改变了气象灾害(旱灾)对水稻产量的影响，但是现有的技术水平并不能完全消除旱灾对水稻生产的影响，而且二者的相关性依然较高。

图2 玉米和未受旱灾比率Z的动态下尾相关系数

图2所示的玉米和未受旱灾比率Z的动态下尾相关性则反映了不同的情形。除了样本中前几个个别年份，玉米产量和旱灾强度几乎始终保持较高的相关性，没有表现出随时间变化的时变性。自20世纪80年代后，玉米单产和未受旱灾比率的动态下尾相关系数几乎都保持在0.5—0.8的区间内。

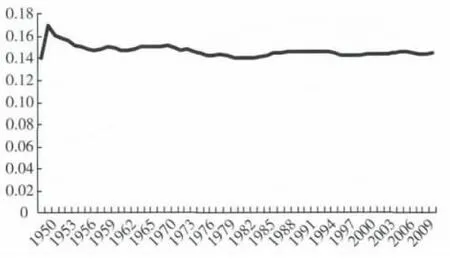
图3 小麦和未受旱灾比率Z的动态下尾相关系数

图3显示的是小麦和未受旱灾比率Z的下尾相关系数的变化规律。相对于玉米和水稻，小麦单产和未受旱灾比率Z的下尾相关系数略小一些，但是随着时间的推移，技术的进步并未影响到小麦低产与旱灾之间的尾部相关性。从图上看，相关系数基本保持在0.15附近。

比较图1、图2和图3，旱灾对水稻、玉米和小麦这三种粮食的产量都产生了影响，其中影响程度最严重的是玉米，其次是水稻，影响程度相对较低的是小麦。从时间动态性来看，玉米和小麦对旱灾的依赖性并未随着时间的推移而有明显的降低。这说明，对于玉米和小麦而言，技术进步在改善玉米、小麦的耐旱性方面尚未取得显著的成果。因此，改良玉米、小麦的品种，增强其耐旱性，改善玉米种植区的灌溉条件是一项迫切的任务。对于水稻而言，技术进步在增强其耐旱性方面成果显著，因为随着时间的推移，粮食低产和自然灾害之间的下尾相关性显著下降了。

四、结 论

现有文献在研究气象灾害对粮食产量的影响时，多隐含着假定天气变量和粮食产量存在线性关系的前提条件，且假定产量对天气变量的依赖关系保持不变。为了克服上述不足，本文利用Copula函数研究了旱灾对水稻、小麦和玉米等三种粮食单产的动态尾部相关性。研究结果表明，水稻、小麦、玉米与未受旱灾影响的关联性表现出非对称性，下尾相关程度很高，而上尾相关性较低，这说明旱灾是导致粮食减产的重要原因。从动态影响效应看，旱灾对粮食产量影响的时变性因不同作物而异。对于水稻而言，随着技术水平的提高，旱灾与水稻单产的关联性有显著的下降，但是，对于小麦、玉米而言，旱灾与单产的关联性并没有随时间的推移而下降。无论是小麦、玉米还是水稻，在当前的技术水平下，旱灾都显著影响着产量。这些结果说明，虽然技术的提高在一定程度上降低了气象灾害对粮食生产的影响，但并不能完全消除气象灾害的影响，因此，防灾抗灾的形势依然严峻，农业气象灾害风险管理依然是我国今后的重要课题之一。

［1］ 李茂松，李章成，王道龙，等.50年来我国自然灾害变化对粮食产量的影响［J］.自然灾害学报，2005，(2).

［2］ 王春乙，娄秀荣，王建林.中国农业气象灾害对作物产量的影响［J］.自然灾害学报，2007，(5).

［3］ 龙方，杨重玉，彭澧丽.自然灾害对中国粮食产量影响的实证分析——以稻谷为例［J］.中国农村经济，2011，(5).

［4］ 卢丽萍，程丛兰，刘伟东，覃志豪.30年来我国农业气象灾害对农业生产的影响及其空间分布特征［J］.生态环境学报，2009，(4).

［5］ You Liangzhi，Wood Stanley，Rosegrant Mark W.，Fang Cheng.Impact of Global Warming on Chinese Wheat Productivity［P］.Washington:International Food Policy Research Institute，2005.

［6］ Lin Tun，Liu Xiaoyun，Wan Guanghua，Xin Xian，Zhang Yongsheng.Impact of Climate Change on the People's Republic of China’s Grain Output——Regional and Crop Perspective［P］.Manila:Asian Devolopment Bank，2011.

［7］ 崔静，王秀清，辛贤，吴文斌.生长期气候变化对中国主要粮食作物单产的影响［J］.中国农村经济，2011，(9).

［8］ Bokusheva R.Measuring dependence in joint distributions of yield and weather variables［J］.Agricultural Finance Review，2011，(71).

［9］ 谢凤杰，王尔大，朱阳.基于Copula方法的作物收入保险定价研究——以安徽省阜阳市为例［J］.农业技术经济，2011，(4).

［10］ Joe Harry.Multivariate Models and Dependence Concepts［M］.London:Chapman ＆ Hall，1997.

［11］ Patton Andrew J.Modelling Asymmetric Exchange Rate Dependence［J］.International Economic Review，2006，(2).

［12］韦艳华，张世英，郭焱.金融市场相关程度与相关模式的研究［J］.系统工程学报，2004，(4).

［13］ Diebold F.X.，Gunther T.，Tay A.S.Evaluating Density Forecasts with Applications to Financial Risk Management［J］.International Economic Review，1998，(39).Diebold F.X.，Hahn J.，Tay A.S.Multivariate Density Forecast Evaluation and Calibration in Financial Risk Management:High Frequency Returns on Foreign Exchange［J］.The Review of Economics and Statistics，1999，(4).