探研偶数阶微分方程主次特征值之比的下界*

黄振明，陈 军

（苏州市职业大学基础部，江苏苏州 215104）

探研偶数阶微分方程主次特征值之比的下界*

黄振明，陈 军

（苏州市职业大学基础部，江苏苏州 215104）

考虑偶数阶微分方程在Dirichlet和Neumann边界条件下广义特征值的估计，利用方程特征值理论、分部积分、测试函数、广义Rayleigh定理和不等式估计等方法，获得了主次特征值之比的下界估计不等式，且估计值与区间的几何量无关.

微分方程;主、次特征值;下界;估计

1 引言

在19世纪30年代，法国数学家斯图姆（Sturm）和刘维尔（Liouville）详细讨论了如下一个二阶线性常微分方程零边值问题，即后人所谓的S－L问题，

建立了有关特征值、特征函数空间最初的完整理论，自此开创了各种特征值问题的研究，并得到了与上述S－L问题相类似的结论.近年来，学者们将特征值问题推广至广义特征值问题，即在一定边界条件下，研究微分方程（组）Ay=λBy，其中A，B为线性微分算子，特别在特征值估计方面取得了一系列成果［1－8］，其中文［1］和文［2］分别讨论了一类四阶和六阶微分方程广义特征值的上界估计，笔者将文［1］和文［2］中的方程进行推广，并将权推广至x的任意函数s（x），考虑如下一般情形的偶数阶微分方程（1）的广义特征值估计问题

其中（a，b）R是一个有界区间，a＜b，正整数n3，p（x）∈Cn（［a，b］），q（x）∈C（［a，b］），q（x）0，s（x）∈C1（［a，b］），且满足

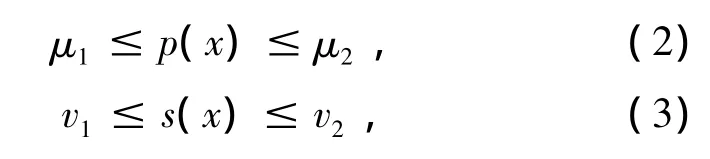
其中 μi，vi（i=1，2）为正常数.

笔者参照并改进文［3］中的讨论方法，得到了如下的主要结果.

定理1 设λ1，λ2是问题（1）的主、次特征值，则有估计式

2 定理的证明

设问题（1）的主、次特征值分别为 λ1，λ2，由微分方程特征值理论知0＜λ1λ2，又记λ1相应的主特征函数为y，且满足即

由式（3）和（5）可得

引理2 设λ1是问题（1）的主特征值，则当n3时，下列不等式成立.

再将引理4的估计结果代入上式左端，化简便得定理的式（4）.

3 结语

特征值估计是特征值研究的重要内容之一，本文考虑了偶数阶常微分方程（1）的广义特征值估计，获得了主、次特征值之比的下界估计不等式，其估计系数与所论区间的几何量a，b无关，文［1］讨论的方程是本文方程（1）当n=2时的特例，文［2］讨论的方程也是本文方程（1）当n=3，q（x）=0，s（x）=1时的特例，因此本文的结果是文［1］和［2］的进一步推广，在特征值数值定量分析中有着一定的参考和应用价值［9－10］，至于问题（1）中的方程在其它边界条件下是否有类似式（4）的特征值估计结论还有待于进一步研究.

［1］黄振明.一类四阶微分方程第二广义谱的估计［J］.三明学院学报，2011，28（5）:13 －16.

［2］韩秋敏，钱椿林.六阶某类微分方程第二特征值的上界［J］.苏州大学学报，1999，15（4）:26 －30.

［3］赵晓苏，钱椿林.六阶微分系统带权第二特征值的上界［J］.长春大学学报，2010，20（8）:10 －13.

［4］曾维国，钱椿林.斯图姆－刘维尔问题的特征值［J］.工科数学，1992，8（1）:28 －32.

［5］金光宇，钱椿林.四阶常微分方程的特征值估计［J］.苏州丝绸工学院学报，1996，16（4）:115 －119.

［6］黄振明.六阶常微分方程的特征值的上界估计［J］.江苏广播电视大学学报，2005，16（3）:68 －70.

［7］吴平，钱椿林.高阶常微分方程特征值的上界估计［J］.苏州铁道师院学报，2001，18（3）:3 －9.

［8］贾高.梁横向振动方程的特征值估计［J］.安徽大学学报，1997，21（2）:29 －33.

［9］Hile G H.and Yen R Z.Inequalities for Eigenvalues of the Biharmonic Operator［J］.Pacific J Math，1984，112（1）:115 －132.

［10］Protter M H.Can one hear the shape of a drum［J］.SIAM Rev.1987，29（2）:185 －197.

Lower Bound Estimate of Ratio of Principal Eigenvalue to Secondary Eigenvalue for Even－order Differential Equation

HUANG Zhen － ming，CHEN Jun
（Department of Basic Courses，Suzhou Vocational University，Suzhou，Jiangsu 215104，China）

This paper presents the generalized eigenvalue estimate for even－order differential equation under the Neumann boundary condition as well as Dirichlet.The inequality of the lower bound of the ratio of principal eigenvalue to secondary eigenvalue is estimated by using eigenvalue theory of equation，integration by parts，trial function，generalized Rayleigh theorem and inequality estimate etc.The estimate is irrelevant to the geometric sense of the domain.

differential equation;principal and secondary eigenvalue;lower bound;estimate

O175.1

A

1008－7974（2014）03－0024－04

2013－12－20

黄振明（1962－），江苏苏州人，副教授.

（责任编辑:王宏志）