六阶电力系统动力学分析及其参数自适应滑模控制

鲁升敏， 王江彬， 刘崇新

(1.陕西省地方电力有限公司， 陕西 西安 710061； 2.西安交通大学 电气工程学院， 陕西 西安 710049)

电力系统作为典型的动力学工程实际系统，其往往呈现多种复杂的动力学行为。研究表明，电力系统也会和其它众多非线性系统一样在特定参数及初始值条件下呈现混沌状态[1-2]。人们已经提出了众多控制方法抑制电力系统混沌，然而目前大量研究工作仍然集中在二阶电力系统模型[3-7]。

近年来，人们开始研究典型三母线电力系统混沌振荡行为并为其设计控制器。三母线电力系统的主要动力学模型包括四阶模型、六阶模型以及更为复杂的七阶模型[8-10]。为了控制四阶电力系统的混沌振荡，文献[11]基于有限时间稳定理论提出了有限时间反馈控制，文献[12]提出了性能更为优越的固定时间积分滑模控制，文献[13]则基于LaSalle不变集理论提出了形式简单的自适应反馈控制，该控制方法的突出特点在于所需电力系统模型的信息量很少。另外，文献[14]在考虑系统干扰的条件下为该系统提出时标分离滑模控制。四阶模型可以通过对六阶模型化简得到，针对更为复杂的六阶模型提出的混沌控制方法必然更加具有普适性。

六阶电力系统动力学模型由于模型本身的复杂性所致，因此无法按照文献[15-16]分析及控制简单系统的方法通过解析运算求取系统平衡点与Jacobi矩阵，也难于采用诸如文献[17]对简单二阶电力系统混沌振荡条件进行解析分析的方法对六阶电力系统模型进行类似的分析。这给系统的分析与控制问题带来困难，也将六阶电力系统的分析及控制问题与简单系统明显相区别。目前来说，研究这类复杂系统模型的主要方法仍然是计算机数值仿真方法[8-10]。文献[18]为六阶混沌电力系统提出了自适应协同控制，为该动力学系统的混沌控制问题提供了思路。然而，一方面尚需要对该系统模型中的动力学行为进行分析，另一方面仍然有必要针对该复杂电力系统模型进行混沌控制研究。

为了更进一步对六阶混沌电力系统进行分析与控制，首先利用混沌理论的分岔图、相图以及频谱图对六阶电力系统的动力学行为进行分析，并在系统中捕获到了多涡卷吸引子等动力学现象。然后在考虑参数不确定条件下为其设计参数自适应滑模控制器，利用Lyapunov稳定性方法证明了在控制器的作用下受控系统能够实现控制目标，从而消除了系统中的混沌振荡等复杂动力学行为，使整个受控电力系统能够恢复至稳定运行状态。

1 系统模型及其动力学分析

六阶电力系统模型可以由七阶电力系统模型简化而来[10]，在原有六阶电力系统模型的第二个方程、第五个方程以及第六个方程施加控制器之后构成的受控电力系统动力学模型表述为：

(1)

式中：δm与sm分别表示发电机功角与频率偏差；

令控制输入u1=0、u2=0、u3=0，则系统(1)为原有六阶电力系统动力学模型。系统(1)的参数中，Pm表示发电机机械输入功率，以该参数作为分岔参数对系统呈现的复杂动力学行为进行数值仿真分析。取参数区间Pm∈[0.65,1.129]，利用最大值法绘制系统状态δm随参数Pm变化的分岔图见图1。

图1 系统状态δm随参数Pm变化的分岔图Fig.1 Bifurcation diagram for system state δm varying with parameter Pm

图1结合系统相图表明，系统状态在参数区间Pm∈[0.65,0.83]内表现为周期1运动，在该区间内取参数值Pm=0.7，绘制的系统相图见图2(a)。在参数区间Pm∈[0.84,1.04]内表现为拟周期运动，在该参数区间内取值Pm=0.9，得到的系统相图见图2(b)。在参数区间Pm∈[1.05,1.09]内表现为周期3运动，在该参数区间内取值Pm=1.07，得到的系统相图见图2(c)。而当Pm∈[1.1,1.129]时，系统状态进入混沌态，同样在参数区间内取值Pm=1.129，得到系统相图见图2(d)和图2(e)，明显系统状态在这两个相图上表现为奇怪吸引子。而当Pm>1.129时，会在多个参数区间出现系统状态发散的情况，因此选取的参数区间上界为Pm=1.129。然而，在Pm>1.129时系统状态的相图会在某些参数区间表现为多涡卷吸引子，而且随着系统仿真时间的增加涡卷的数目会持续增多。取参数Pm=1.146 5，仿真时间为t=100 s，得到的系统相图见图2(f)。这里绘制相图时选取的是具有典型特征的相平面。

图2 六阶电力系统在不同分岔参数条件下的相图Fig.2 Phase diagram for six-dimensional power system with different bifurcation parameters

为了更进一步证实系统(1)在参数Pm=1.129与Pm=1.146 5条件下的振荡形式是混沌振荡，取仿真时间t=600s，得到参数Pm=1.129时状态变量δm与VL的频谱图见图3(a)和图3(b)。同样，参数Pm=1.146 5时状态变量sm与VL的频谱图见图3(c)和图3(d)。对应每个状态变量均可以绘制对应的频谱图，这里选取的也是具有典型特征的频谱图。由图3可知，六阶电力系统在这些参数条件下的频谱图是具有混沌振荡典型特征的连续谱。包括混沌振荡在内的电力系统复杂动力学行为有可能对电力系统稳定性造成危害，因此有必要对其进行控制。

图3 六阶电力系统在不同分岔参数条件下的频谱图Fig.3 Spectrum of six dimensional power systems with different bifurcation parameters

2 参数自适应滑模控制器设计

复杂电力系统模型的控制目标要能够兼容简单系统模型的控制目标。二阶电力系统模型的控制目标多为使系统恢复到同步运行状态[3-7]，而控制四阶电力系统模型需要使电力系统恢复同步并将其负载母线电压幅值控制到额定值[19]。为此，系统(1)的控制目标设为使电力系统恢复到同步运行状态并将负载母线电压的相角及幅值控制到额定值，即具体控制目标设为：δmd=0，δLd=0，VLd=1。为了利用滑模控制方法为系统(1)设计混沌控制器，定义滑模函数：

(2)

式中：λ1>0。

定义式(2)的滑模函数之后，就可以将系统(1)的控制目标表述为：设计控制器u1、u2、u3，使系统(1)的状态分别到达滑模面：{S1|S1=0}，{S2|S2=0}，{S3|S3=0}。

(3)

(4)

式中：K1>0，K2>0，K3>0；f1、f2、f3表示系统函数，具体的表达式为：

(5)

证明：构造正定的Lyapunov函数：

(6)

则该函数关于时间的导数为：

S3{f3-(P1d/p2)+[p1/(q1p2)]Q1d+u3}+

(7)

(8)

3 控制效果数值仿真

为验证控制方法的有效性，可以为系统(1)的分岔参数Pm取不同的值，以使得系统状态呈现如图2所示的不同状态。取参数值Pm=1.129以使得系统呈现图2(d)与图2(e)所示的混沌状态，并在该参数条件下对控制器的有效性进行验证。控制器参数取λ1=2，K1=10，K2=10，K3=10，由式(2)及式(4)可知只要这四个参数取正值即可，具体取值时还可以人为调整。控制器投入运行后，受控六阶电力系统及参数自适应律的时域波形见图4，该图说明六阶电力系统由混沌状态恢复到平衡态，自适应参数也恢复稳定，从而使整个电力系统恢复至稳定运行状态。

图4 混沌状态条件下受控六阶电力系统的时域波形Fig.4 Time responses of controlled six-dimensional power system under chaotic state condition

图5给出了六阶电力系统状态的演化过程图，正如该图显示，未受控的电力系统状态在相图中表现为奇怪吸引子，而控制器投入运行后系统状态在δm-sm相平面中由奇怪吸引子经状态演化轨迹L1最终到达目标点O1(0,0)，在δm-VL相平面中也由奇怪吸引子经状态演化轨迹L2最终到达目标点O2(0,1)，从而在考虑参数不确定条件下实现了该复杂动力学系统的控制。

图5 混沌状态条件下六阶电力系统的状态演化过程图Fig.5 State evolution process of six-dimensional power system under chaotic state condition

当然，Pm的值完全可以取Pm=0.9或者Pm=1.146 5，以使得系统状态呈现图2(b)或图2(f)所示的拟周期状态或者多涡卷吸引子状态，即验证控制器的有效性时完全可以使系统状态呈现拟周期状态或者多涡卷吸引子状态。控制参数不变，将系统分岔参数取值为：Pm=0.9，这时系统状态在相图上表现为如图2(b)所示的拟周期吸引子。在该运动状态条件下投入所设计的控制器，可得到电力系统状态演化图如图6所示，该图说明控制器能够实现与图5类似的控制效果，受控系统的状态在相图上也经由一定的演化轨迹逐渐运动到控制目标点。图7则给出了当分岔参数Pm=1.146 5，系统状态呈现如图2(f)所示的多涡卷吸引子状态条件下的系统状态演化图，所得到的控制效果类似于图5和图6的仿真结果。拟周期状态与多涡卷状态条件下受控电力系统的时域响应波形也和图4呈现的结果相似。控制器在系统运行的三种状态条件下均能够控制复杂六阶电力系统中的动力学行为，这都证实了所设计控制器的有效性，也意味着控制器对重要参数Pm的变动具备一定的鲁棒性。

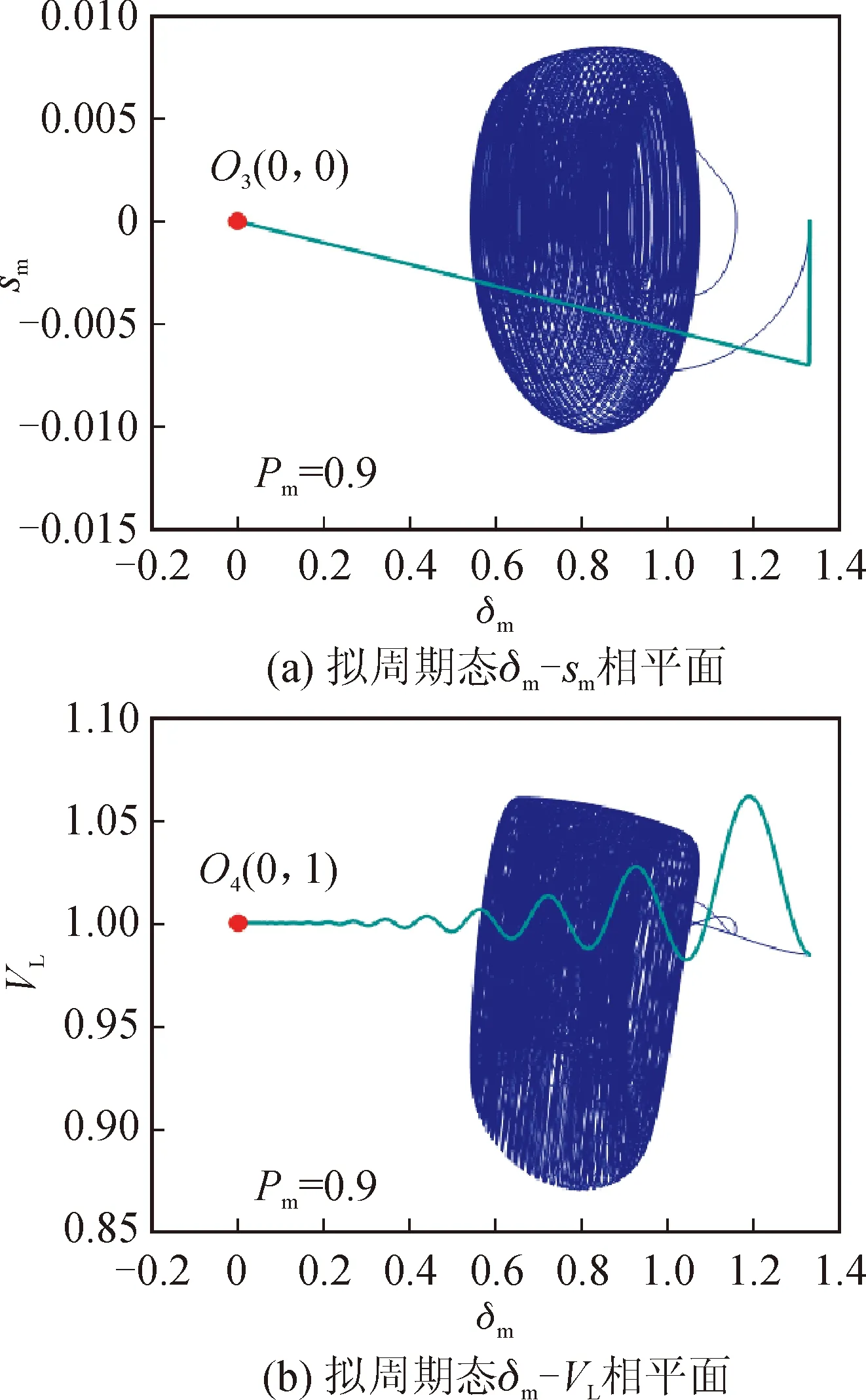
图6 拟周期状态条件下六阶电力系统的状态演化过程图Fig.6 State evolution process of six-dimensional power system under quasi periodic state condition

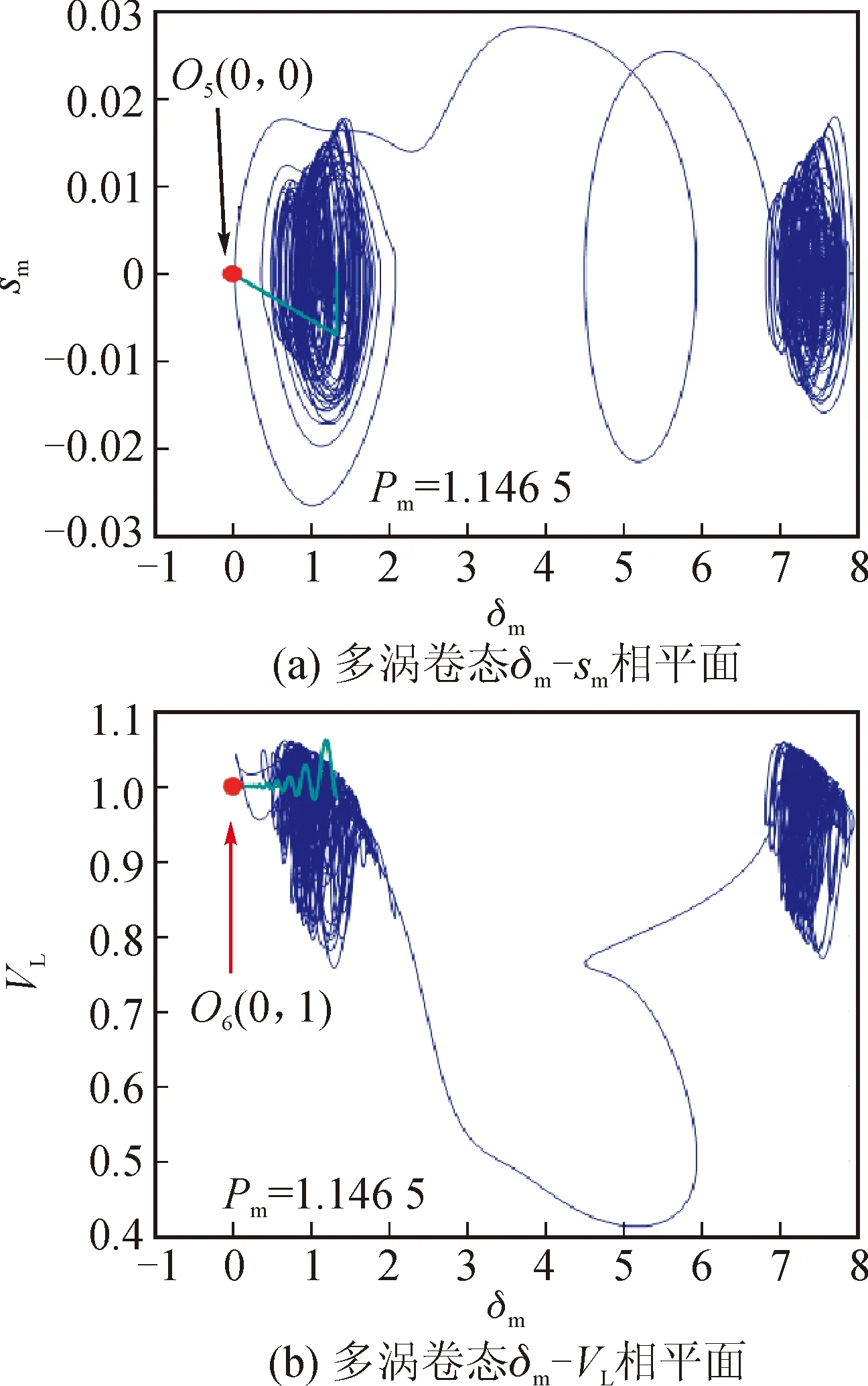
图7 多涡卷状态条件下六阶电力系统的状态演化过程图Fig.7 State evolution process of six-dimensional power system under multi-scroll chaotic state condition

4 结 论

1) 通过混沌理论中的分岔图、相图以及频谱图分析得出，六阶电力系统存在复杂的动力学行为，包括周期运动、拟周期运动、混沌运动，并出现了多涡卷吸引子现象。

2) 考虑参数不确定条件下，所设计的参数自适应滑模控制器可以控制六阶电力系统中的复杂动力学行为，并使系统能够恢复到稳定运行状态。控制效果仿真证实，控制器在系统呈现混沌状态、拟周期状态以及多涡卷吸引子状态三种条件下均能够实现控制目标。

3) 注意到控制目标为使电力系统恢复到同步运行状态并将其负载母线电压控制到额定值，这与四阶电力系统及二阶电力系统的控制目标是相兼容的。也说明电力系统混沌控制完全是一个电力系统控制问题，应从电力系统控制的角度为混沌电力系统设计控制器。本文的研究结论可以为电力系统高维复杂动力学系统模型的混沌控制提供借鉴。