神经网络定位中多点多映射概率样本增强方法研究

杨 静， 曹秀伟

(1.西安理工大学 机械与精密仪器工程学院, 陕西 西安 710048；2.中建科技集团有限公司深圳分公司, 广东 深圳 518000)

随着无线网络、大数据等技术的不断发展，基于位置服务的应用需求快速增长，普及到了社会生活和生产的各个领域[1]。基于无线信号RSSI(强度接收指示，received signal strength indication)的定位技术，由于成本低，使用灵活等优点得到广泛的应用[2]。基于RSSI信号定位精度的关键在于如何建立尽可能多的有效的信号强度指示与空间物理位置的映射关系。过去研究者们通常采用KNN[3]等匹配算法进行定位，但是却无法保证实时性与精度同时提升。而神经网络凭借自身的易用性、鲁棒性以及强大的非线性拟合能力，近几年在定位应用领域逐渐受到关注[4]。神经网络算法的性能很大程度上取决于训练样本，在定位算法中，只有当训练样本足以表征不同位置信号RSSI特征，才能保证网络学习模型其具有泛化能力。根据无线信号传播特点，在复杂环境中，人员、墙体以及其他障碍物，都会给RSSI信号带来非视距以及多径效应的不确定性[5]。大量研究表明，利用概率论与数理统计的方法处理RSSI信号的不确定性[6]，具有较好的抗噪声性能，可极大地去除信号中的噪声，有效提高定位精度。然而，现有的神经网络定位算法利用大量实测RSSI数据,通过人工提取数据的均值、方差等特征样本对神经网络进行训练[7-8]。这种方法不仅人工成本高，而且不能有效表征无线信号的不确定性。文献[9]提出了一种多信息融合的位置指纹采集方法，利用航位推算与步态分析生成指纹，降低了人工采集工作量，但指纹数据精度较低。2020年成意等[10]提出了群智指纹库建立方法，利用聚类算法指纹数据进行扩展，建立了RSSI信号的Rice模型，信号的表征性较好，但模型参数受位置影响，运算复杂不利于工程实践推广。本文以推进指纹法在工程实际中的应用为出发点，利用无线信号的传播特性、空间相关性以及信号的Gauss分布模型对有限的实测数据进行扩充，从而构建多点多映射概率特征样本。利用扩充样本训练RSSI神经网络位置模型，相比少样本的训练模型，可以提高蓝牙RSSI的室内定位精度。

1 RSSI信号传播模型与特征

无线信号从发射端经过无线信道到达接收端，根据环境不同，传播过程存在大尺度与小尺度两种衰减特性。其中，大尺度衰减又包括路径损耗和阴影衰落。路径损耗是由信号传播距离以及信号载频导致；阴影衰落主要是由于建筑物、高山等对信号的阻挡导致。小尺度衰减是由于建筑墙体、地板或家具等导致的无线信号多径传播效应。大尺度衰减特性描述信号在大距离(室外环境是10～100 m，室内更小)上信号强度变化。小尺度衰减特性描述信号在小距离(波长数量级)上信号强度变化，因此，大尺度衰减是影响RSSI定位的主要因素。在无线信号传播中，由于障碍物的反射、折射导致信号随机变化，实验结果表明[11-12]，在一定空间位置上的RSSI信号呈现随机波动，信号强度服从正态分布的分布，其概率密度函数表示为：

(1)

式中：f(x)表示信号强度为x的概率；μ为信号均值，与无线信号传播距离以及环境有关；σ为信号标准差(方差)，描述了信号波动。自由空间(弱干扰空间)无线信号阴影传播模型为：

μ=A+10nlgd

(2)

式中：d为无线信号接收点与发射点之间的距离；n为受环境影响的路径损耗因子；A为单位距离(1 m)处的信号强度RSSI值；μ为d米处接收信号的RSSI值。模型(2)反映了自由空间传播距离d以及信号波长等无线硬件特性对接收信号均值的影响，但在复杂传播环境中，无线信号均值μ以及方差σ都会受环境影响。

2 多映射概率特征样本增强算法描述

在神经网络的训练中，样本数量以及样本对数据特征的表征性，直接影响网络的性能。通常研究者们会采用插值算法[13]对指纹数据进行扩充，但该方法无法表征环境影响与数据特征。本文提出了对有限实测数据的增强算法，其增强数据可以有效体现受实际环境的影响数据的特征，为神经网络训练提供大量有效样本。首先在自由空间拟合无线信号阴影传播模型(式(2))，并生成多点特征。然后，利用无线信号的空间相关性，对多点特征进行环境修正。最后，构建多映射概率特征样本，反应信号的波动特征。本文提出的多点多映射样本增强算法流程见下。

第一步：自由空间阴影传播模型拟合。

固定一个锚节点，获取不同距离d的信号强度RSSI，通过Kalman滤波[14]处理得到均值μ，再利用最小二乘法拟合无线信号阴影传播模型(2)中的参数n。

第二步：生成实测样本特征集z1。

根据实际定位环境的干扰情况，选取m个能够代表整个定位空间环境因素的实测采样点，读取每个实测采样点的RSSI样本数据，通过Kalman滤波可得实测样本数据的均值μ1以及方差σ1，由m个实测样本点均值构成的实测样本特征集z1。以图1三个锚节点A，B，C构成的三角形定位空间为例，选图中标记的m个实测点(g1，g2，…，gm)为实测样本集。

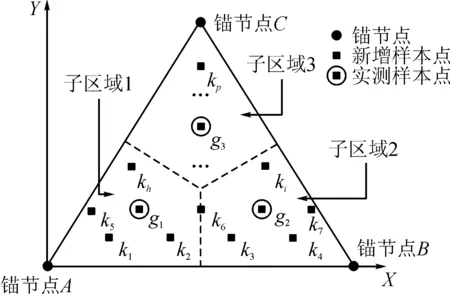
图1 三锚节点定位空间的样本点与子区域Fig.1 Sample points and sub-regions of the three-anchor node positioning space

第三步：生成特征的环境影响量σ以及Δμ。

考虑到环境对RSSI信号的影响，本文定义环境对RSSI信号的环境影响量为自由空间的阴影传播模型(2)计算的采样点RSSI特征与实测RSSI特征的差。因此，根据自由空间的阴影传播模型(2)计算第二步中m个实测采样点的计算均值μ0，以及结合实测样本的均值μ1可以得到m个采样点特征的环境影响量：Δμ=μ1-μ0；σ1=σ0。

第四步：构建新增样本点特征值并修正。

根据无线信号传播的空间相关性，可以认为一定半径范围区域内，环境对无线信号的影响相同[15]。因此，以实测样本点为聚类中心，将定位空间划分成若干个子区域，每个子区域包含一个实测点，在同一区域内新增样本点与实测点受环境影响是相同的。

在图1中，m个实测点将ABC三角区域分为m个子区域，图1中用虚线分割。在三角区域ABC中随机新增p个样本点(k1，k2，…，kp)(图中■标记位置)。首先利用每个新增样本点的位置信息，通过无线信号阴影传播模型(2)可以得到新增样本点RSSI计算均值μp0，然后，根据每个新增样本点所在子区域，对新增样本的特征进行环境修正，修正均值为μp=μp0+Δμ，修正方差为σp=σ1。

第五步：生成增强样本特征集z2。

实测样本点特征(μ1，σ1)与新增样本点特征(μp，σp)共同组成具有(m+p)个点的增强样本特征集z2。

第六步：生成多点多映射概率分布样本集z3。

根据RSSI信号分布模型(式(1))，由增强样本点的均值与方差，按正态分布在每个样本点生成N个多映射样本。即由m个实测样本，增强为(p+m)N个Gauss概率分布的多点多映射样本集z3，该增强样本集更好地反应了环境对无线信号的衰减以及波动影响。

利用上述方法我们可以根据定位区域环境干扰程度不同，自适应构建不同定位区域的多点多映射概率增强样本集。

3 实验结果与分析

3.1 实验环境与过程

图2是某地下车库的实验场景，该场地为半开放式复杂场景。图3为该地下车库的俯视图，车库长约38.8 m，宽约27.5 m，高约5 m。车库为双层金属结构车库，车库中有通道1、2、3，图3中灰色■部分为混凝土障碍立柱，黄色部分是停车区，在通道3两侧以及车库四周有混凝土墙，车库顶部以及停车区内有大量金属材质障碍物。该实验环境复杂，实验结论具有说服力。

图2 地下车库实验实景图Fig.2 Experimenton the underground garage

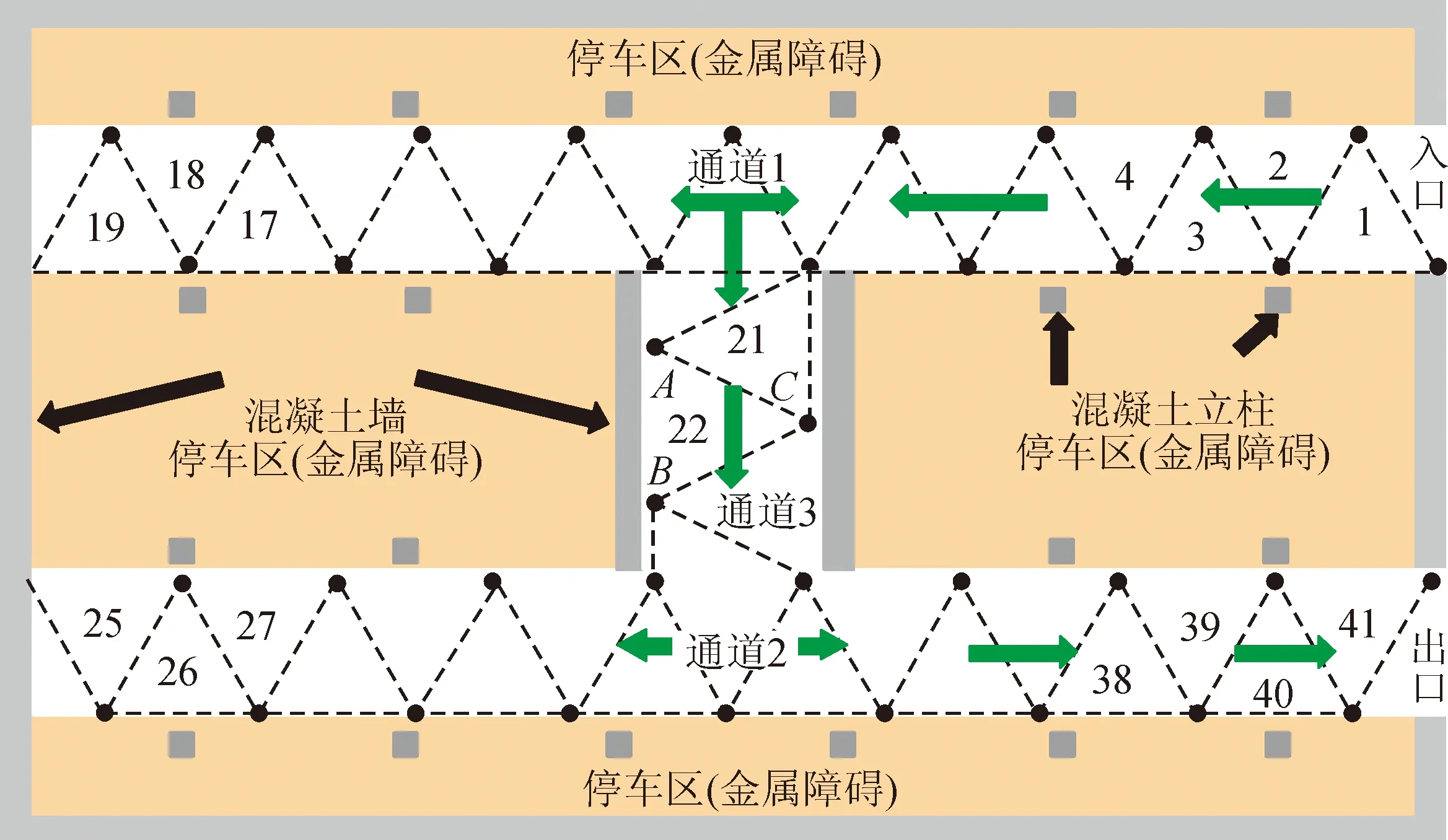
图3 实验场地锚节点布局Fig.3 Layout of anchor nodes in the experimental site

本实验采用蓝牙技术[16]对该地下车库中人员进行定位。实验采用蓝牙信号采集模块(锚节点)为深圳瑞迪莱科技公司的NRF52832；蓝牙信号发射模块(信标)为北京四月兄弟科技的April Beacon N04。根据文献[17]可知，当3个锚节点以最佳测量半径为边长布局为等边三角形时，待定位点在三角形区域内的定位精度最高，故本实验在待定位区域内锚节点布局见图3(图中●为锚节点)。每3个锚节点构成一个待定位区域，相关运算在图中22号定位区域内进行。

首先，在自由空间对所使用的蓝牙锚节点以及信标进行不同距离处RSSI的测量，拟合得到蓝牙模块的阴影传播模型：

μ=-35.7+8.8lgd

(3)

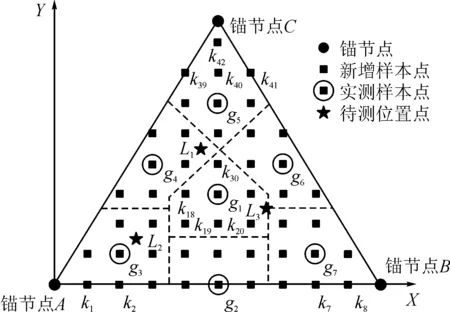
图4 22号定位区域样本点布局图Fig.4 Layout of sample points in No.22 positioning area

图5中虚线为三个锚节点读取g1点信标的RSSI实测样本数据，实线为滤波后的数据，可见RSSI滤波后的数据仍然呈现随机波动，利用滤波后数据可得均值μ1。图6为滤波后RSSI的概率分布直方图，可见接收的RSSI信号基本呈正态分布，计算可得方差σ1。

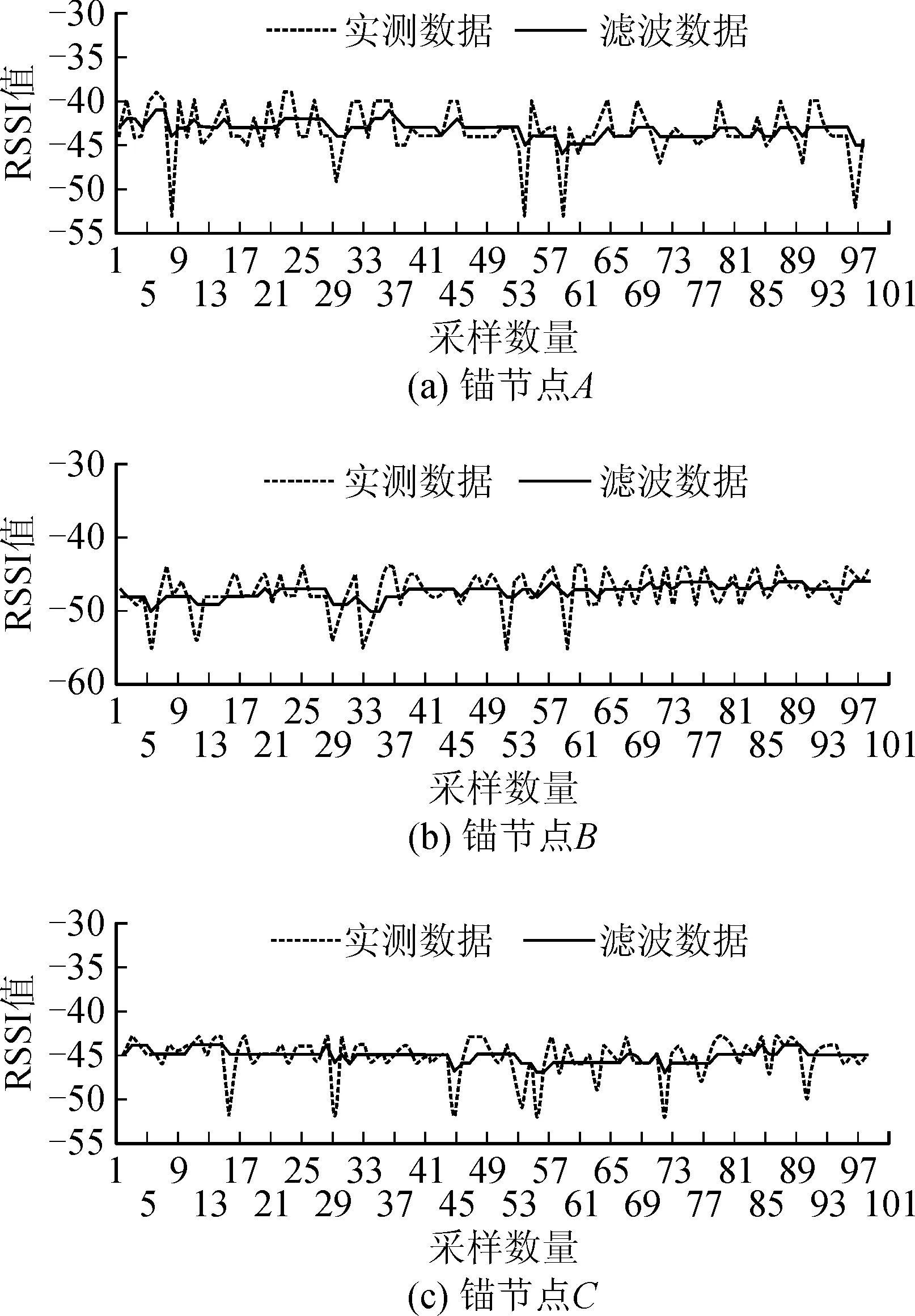
图5 三个锚节点读取实测点g1的RSSI值Fig.5 Three anchor nodes read the RSSI value of the measured point g1

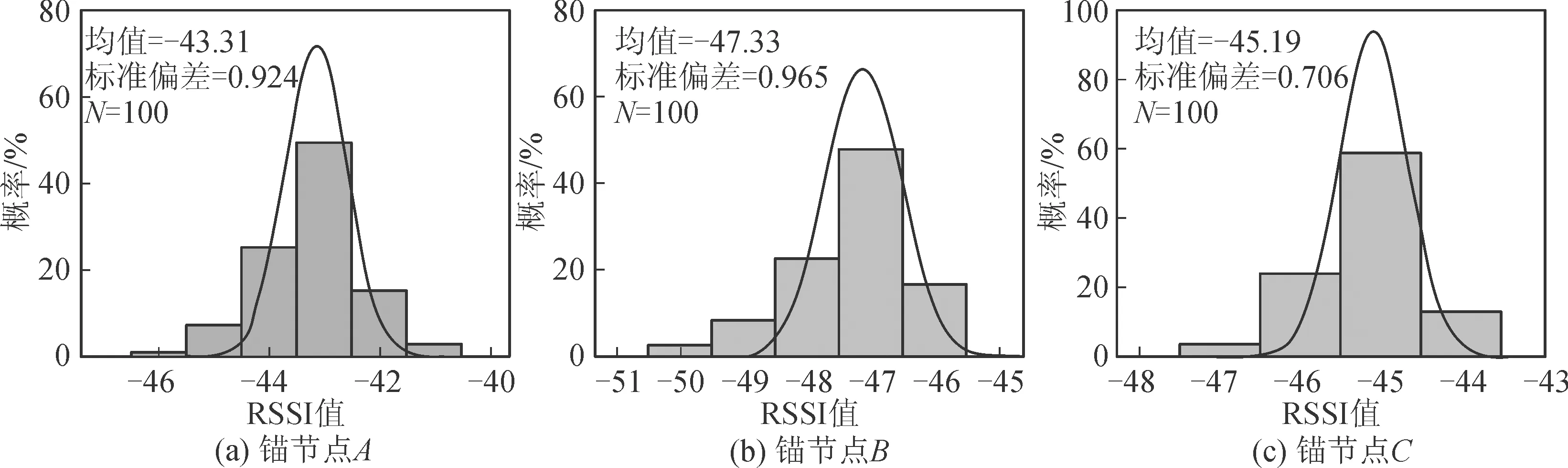
图6 实测点g1滤波后RSSI概率分布直方图Fig.6 Histogram of RSSI probability distribution after filtering of measured point g1

然后，将定位空间分为7个子区域，并新增42个样本点■，见图4。利用模型(3)以及无线信号传播的空间相关性，可以得到增强样本的特征集z2。之后利用增强样本点的均值与方差，通过MATLAB函数normrnd，在每个样本点各生成100个正态分布的样本，得到4 900个多点多映射概率样本集z3。

3.2 实验结果分析

1) 增强样本与实测样本的RSSI误差分析

为了对本文样本增强算法的合理性做评估，通过人工对上述实验中增强的49个采样点进行实测，每个采样点测量100组RSSI值，对实测原始数据滤波后得到49个样本点的实测RSSI的均值μ与方差σ。表1给出了49个采样点对锚节点A，B，C的实测RSSI特征，与本文增强算法得到的样本特征的对比。由表1可见，本文增强方法得到的RSSI与实测RSSI值的均值μ误差为3.9%，方差σ的误差为36.4%。其中，方差特征的误差比较大，是因为实验环境对实测数据的多径效应影响严重，导致测试数据波动大，增强数据更加平稳，消除了环境影响，有利于提高定位精度。

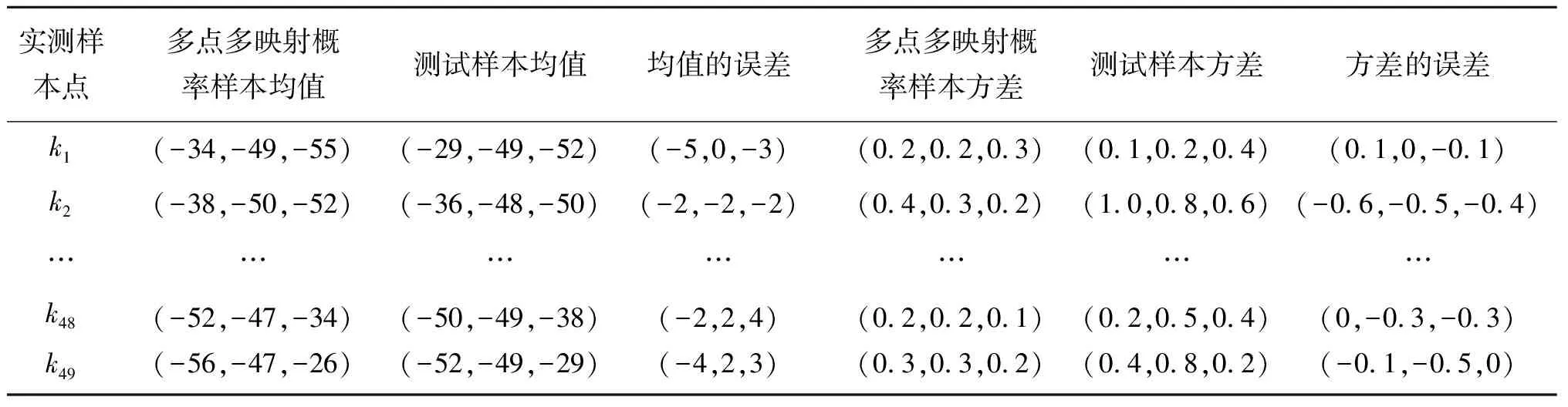
表1 49个实测样本点均值、方差对比Tab.1 Comparison of mean and variance of 49 measured sample points

2) 定位精度分析

利用本次实验的7个实测点特征样本集z1，49个增强样本特征集z2、多点多映射样本集z3，以及对49个全人工采集样本集z4，分别对同参数的BP神经网络进行训练，得到4个不同的定位网络net1，net2，net3以及net4。在图4中任意选取三个待测位置L1,L2,L3(图中★标识)，利用图4中网络分别对每个位置进行5次定位并求均值，得到结果见表2。表中定位误差Δd为待测点理论位置与计算位置之间的欧氏距离。

表2 三种训练样本得到的神经网络定位误差ΔdTab.2 Neural network positioning error Δdobtained by the three training samples 单位：cm

由表2可见，由于7个实测点特征样本的数据量过少，导致网络net1的泛化能力弱，平均定位误差为128 cm，无法在实际工程中应用。网络net2采用了增强的49个特征样本，样本数量增加，且通过修正反应了环境在整个定位空间的影响，网络定位精度提高34.4%，但由于单采集点只有一组均值，数据量过少，无法体现RSSI的概率分布情况，故平均定位精度提高有限。网络net3采用了多点多映射正态分布样本，样本数量多，且更真实反应数据波动，由此训练的网络net3模型定位精度较高，平均定位误差38.5cm，相对网络net2精度提高了50%，与49点全人工采样数据训练的网络net4相比，定位误差仅增加了5.5%。但是从样本集的构建成本分析，多点多映射概率样本增强方法生成的49点样本集仅需7个实测点即可，与人工采集49点样本集相比，人工采集工作量降低了85.7%。综合分析，本文提出的样本增强方法在基于RSSI的神经网络定位算法中应用，人力成本与定位精度综合性能最优。

4 结 论

本文根据自由空间无线信号的传播特性，由少量实测点数据生成定位空间多点特征，并利用空间相关性进行特征的环境修正。最后，利用信号波动的概率特征构建了多映射的正态分布数据样本。实验结果表明，本文提出的多点多映射概率分布样本生成方法，人工成本低，生成的样本能更好地表征数据特征，提高了神经网络的定位精度。但考虑环境对无线信号影响的不确定，如何建立复杂环境的传播模型将是主要的研究方向。