耦合多目标优化和多属性决策的水库生态调度方法研究

刘 艳， 李晓春， 罗军刚

(1.西安理工大学 西北旱区生态水利国家重点实验室， 陕西 西安 710048；2.陕西省江河水库管理局， 陕西 西安 710018)

水库生态调度是在传统水库调度的基础上，将水库和河道的生态服务功能考虑进来的一种新的调度模式。目前已成为国内外水库调度领域的研究热点。在构建生态调度模型时，一般是将生态因子作为约束条件(约束型)或目标函数(目标型)。约束型因其目标函数单一，模型求解较为简单，而被广泛应用。Richter等[1]提出了一个评估水库生态调度的框架，可以用来恢复河道环境流量。Castelletti等[2]为保护河流生态，将最小生态流量作为约束方程加入到水库调度模型中。Gates等[3]对美国Snake河流上的大坝进行生态调度研究时，通过增加季节性枯水流量，进而提高下游生物栖息地的利用性。梅超等[4]对不同生态流量下的调度方案进行研究，分析了水库群的综合效益。范骢骧等[5]建立了一种以鱼类产卵栖息地的生态需水为约束条件的生态调度方法。目标型则是将生态因子作为模型的目标函数，因其更符合多目标问题的本质而受到广泛关注。Halleraker等[6]通过水力-生境模型、IHA指标法、水温模拟法等多种方法计算环境流量，在此基础上进行生态调度。尚文绣等[7]通过水文情势评价指标建立了水库生态调度模型。朱金峰等[8]研究了供水期末生态调度对生态用水产生的影响。张珮纶等[9]建立了基于需水调控策略的最优供水模型。张召等[10]以天生桥一级水库为例，建立了以生态保证率为生态目标的优化调度模型。贾磊等[11]构建了能同时满足生产生活用水和生态需水的水库调度模型。薛耀东[12]通过对水库利益主体及其用水特点的分析，构建了面向生态的水库多利益主体协调调度模型。

目前，水库生态调度研究一直在不断进步和完善。但是大部分将生态作为约束条件，不能达到生态目标与其他目标之间的均衡，其次在目标构建时，没有对目标之间进行定量分析，直接构建模型，对于目标的选择相对不客观。因此，本文以林家村水库为研究对象，在构建模型之前，对各目标之间进行相关分析。为此，本文提出了一种耦合多目标相关分析、多目标优化和多属性决策的、贯通“建模-求解-优选”全过程的一体化水库生态调度方法，为水库生态调度提供一种新的思路和方法。

1 研究区概况

林家村水库位于陕西省宝鸡市以西11 km的渭河峡谷出口处，是一座以农业灌溉为主，兼顾防洪发电和生态供水的水库，具体所在位置见图1。年调节水量0.8亿m3，为宝鸡峡灌区水库补水1.48亿m3，是陕西省重点水利工程。有四个主要部分：主体工程，坝后电站，防护工程和库区淹没处理工程。水库主要特征参数见表1。

表1 林家村水库主要特征参数

图1 林家村水库位置Fig.1 Location of Linjiacun Reservoir

渭水被引入渠道灌溉和发电，有效地缓解了灌区严重缺水的情况。但是同时也带来了生态问题，在枯水期，林家村到魏家堡之间的河道基本处于断流状态，并且生态需水满足率在逐年下降。渭河生态治理进一步增加了对生态用水的需求，使得用水矛盾变得更加突出。因此，为了缓解生态流量不足、保证生态用水需求，开展林家村水库生态调度是很有必要的。

2 调度目标提取及关系分析

2.1 调度目标提取

生态调度是在兼顾水库调度的社会、经济效益的基础上，重点考虑生态因素的水库调度模式[13]。为了合理有效地利用水库水资源，降低不同生态流量指标对水库经济效益产生的影响，本文同时考虑灌溉目标、发电目标和生态目标，建立多目标优化的水库生态调度模型。在构建目标之前，本文对灌溉和发电目标之间进行相关性分析，如果灌溉和发电之间是负相关关系，则建立以灌溉、发电和生态为目标的多目标优化模型；否则，建立以灌溉效益最大、修正全年流量偏差最小为目标函数的优化调度模型。

目标1：灌溉效益最大，可用式(1)表示。

(1)

式中：maxY为最大灌溉效益；Wt为时段灌溉水量；f(Wt)为灌溉水量与灌溉效益的关系。

本文根据文献[14]的研究成果，在不考虑化肥施用折纯量、农业从业人员和农用机械总劳动力变化的情况下，利用面积比拟法，得到宝鸡峡塬上灌区灌溉效益与灌溉水量的效益关系如下：

f(Wt)=7.16×Wt0.087

(2)

目标2：发电效益最大，可用式(3)表示。

(3)

目标3：生态效益最大，即生态AAPFD值最小。采用Ladson等提出的修正全年流量偏差函数(生态AAPFD值)，相关研究表明，生态AAPFD值越小，表示河流生态越好[15]。

(4)

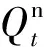
约束条件主要有水位约束、水量平衡约束、出力约束、灌溉需水量约束、机组过流能力约束和渠首引水流量约束等。

2.2 调度目标相关性分析

根据不同典型年(平水年、较枯水年、特枯水年)来水量和灌溉需水量，以文献[16]中计算的生态流量结果作为约束条件(见表2)。

表2 林家村生态流量Tab.2 Ecological flow of Linjiacun

应用NSGA-II算法[17]求解以灌溉和发电为目标函数的双目标调度模型，探究灌溉效益与发电效益之间的关系，结果见图2。从图2中可以看出，平水年，当发电效益小于0.119亿元，发电效益和灌溉效益近似呈线性关系，y1=7.213x+6.684；当发电效益大于0.119亿元，灌溉效益y2=7.725，不再随着发电效益的增加而增加。这是因为灌溉需水量是根据灌溉面积和灌溉定额确定的，不可能是无限大的，当灌溉供水量达到灌溉需水量之后，不会继续增加，这个时候发电引水只会增加发电效益，对于灌溉效益影响不大。较枯水年和特枯水年发电效益与灌溉效益近似呈线性正相关关系。进一步分析发现，发电效益与灌溉效益平水年的相关系数为0.952，较枯水年为0.991，特枯水年为0.984，三个典型年的发电效益与灌溉效益均在99%置信水平下显著正相关。

图2 不同典型年灌溉效益与发电效益关系Fig.2 Relationship between irrigation benefit and power generation benefit in different typical years

为提高水库的综合利用效益，有必要进一步分析生态与灌溉、生态与发电目标之间的相互关系。以特枯水年为例，根据文献[16]中计算的生态流量结果，分别构建灌溉效益最大优化模型，模型目标函数见式(1)；以及发电效益最大优化模型，模型目标函数见式(3)。分别分析计算了生态流量在不同满足度的条件下，林家村水库灌溉效益与林家村断面生态流量的响应关系以及发电效益与生态流量的响应关系。计算结果见图3。可以看出，随着生态流量约束的增加，即年生态需水量的增加，灌溉效益逐渐减少且呈近似线性递减的趋势。林家村水库灌溉效益的变化趋势为：

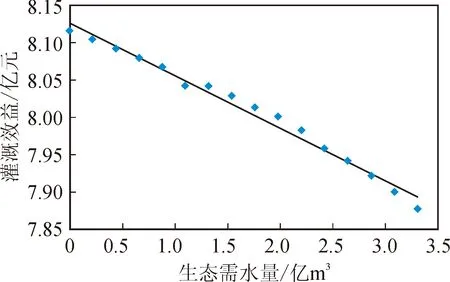
图3 年生态需水量与灌溉效益的关系Fig.3 Relationship between annual ecological water demand and irrigation benefits

y灌=-0.0704q+8.1269

(5)

式中：q为生态流量(m3/s)；y灌为灌溉效益(亿元)。可以看出，生态流量每增加1m3/s，灌溉效益就减少0.070 4亿元。

同样地由图4可以看出，发电效益也随着生态流量约束的增加呈近似线性递减的趋势，发电效益的变化趋势为：

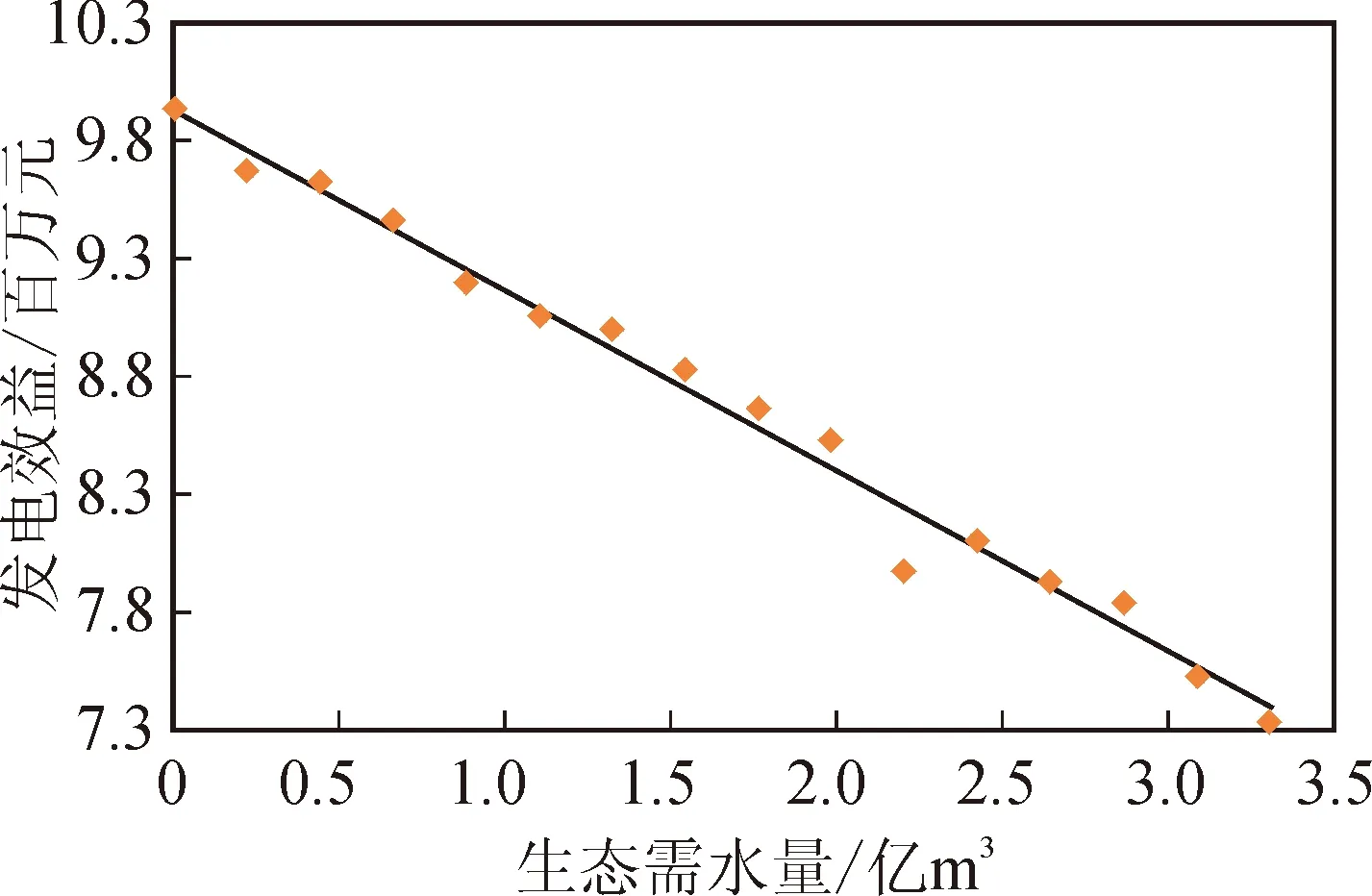
图4 年生态需水量与发电效益的关系Fig.4 Relationship between annual ecological water demand and power generation benefits

y电=-0.7685q+9.9415

(6)

式中：q为生态流量(m3/s)；y电为发电效益(百万元)。可以看出，生态流量每增加1 m3/s，发电效益就减少0.768 5百万元。

通过以上各调度目标之间的相关性分析表明，林家村水库发电与生态、灌溉与生态之间均存在负相关关系。林家村水库的发电效益和灌溉效益存在正相关关系，所以一个目标增大的同时，另一个目标也同步增大，反之亦然。因此，在构建目标时，选择发电效益和灌溉效益这两个目标其中的一个目标即可。林家村水库主要是以灌溉用水为首要目标，发电居于次要地位，结合水库的实际运行情况，由于灌溉放水的不确定性，使得电站无法长期稳定的发电。故本文建立以灌溉效益最大、修正全年流量偏差最小为目标函数，协调建立林家村水库多目标生态调度模型，并采用平水年、较枯水年、特枯水年3个典型年的径流资料计算。

3 多目标调度模型构建与求解

3.1 数学模型构建

依据林家村水库的调度目标之间相关性分析结果，可构建如下的水库多目标调度模型。

目标函数：

MinimizeF=f(-maxY, minR)，t=1,2,…,T

(7)

约束条件：

1) 水库水位过程约束:

Zt,min≤Zt≤Zt,max

(8)

2) 时段出力约束:

Nt,min≤Nt≤Nt,max

(9)

3) 机组过流能力约束:

(10)

4) 水量平衡约束:

Vt+1=Vt+(It-Qt)Δt

(11)

5) 灌溉需水量约束:

(12)

6) 渠首引水流量约束:

(13)

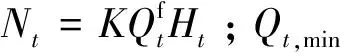
3.2 模型求解算法设计

为解决水库多目标优化求解-多方案偏好选择问题，本文将经典的多目标优化算法(NSGA-II)和多属性决策方法(SEABODE)耦合，建立了一种基于多目标优化-多属性决策的水库生态调度模型求解算法(NSGA-II-SEABODE)。该方法的总体思路是：首先，使用NSGA-II算法[17]解决目标优化问题，以获得备选方案集A；然后，用SEABODE法在方案集A中优选出最终的偏好方案。SEABODE法是一种基于k阶p级有效概念的备选方案逐次淘汰法[18]，与传统方法相比，SEABODE法可直接从决策矩阵中筛选方案，逐步淘汰劣等方案，无需标准化决策矩阵，也无需对属性权重进行计算，因此，降低了方案在优选过程中受到的主观影响。NSGA-II-SEABODE算法的求解流程见图5。

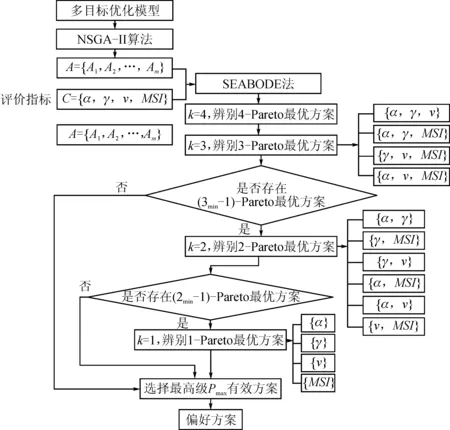
图5 NSGA-II-SEABODE算法流程图Fig.5 NSGA-II-SEABODE combined method flow chart

Step1： 利用NSGA-II算法对多目标优化问题进行求解，得到备选方案集A。

Step2： 基于SEABODE法构建四维属性空间C={α，γ，υ，MSI}对方案集A排序。其中，α为可靠性，γ为可恢复性，ν为脆弱性，MSI为缺水指数。

1) 从k=4开始，在四维属性空间C={α，γ，υ，MSI}中辨别4-Pareto最优方案，找出所有最低阶(记为kmin)。

2) 从选出的四阶有效方案集中进一步向三阶有效方案进行优选，即k=3，此时三阶子空间分别由{α，γ，υ}、{α，γ，MSI}、{γ，υ，MSI}、{α，υ，MSI}构成。

3) 若2)找到的所有kmin-Pareto最优方案中没有一个是(kmin-1)-Pareto最优的，则选择的偏好方案为(kmin-1)阶最高级(pmax)有效方案。

Step3： 重复3)，直到找出[k,p]-Pareto最优方案为偏好方案。

3.3 生态调度方案合理性评价

基于NSGA-II法对水库多目标生态调度模型求解，得到含有100个非劣解的非劣解集，为了找寻综合效益最大的方案，需要对多目标方案进行优选。因此为了进一步淘汰部分较差方案，本文选择可靠性、可恢复性、脆弱性和缺水指数四个评价指标构成水库调度合理性评价指标体系的四维属性空间C={α，γ，υ，MSI},其中α，γ为最大化类型属性指标；ν和MSI为最小化类型属性指标。然后，采用SEABODE方法从备选方案集A的100个方案中筛选出最终的偏好方案。

1) 可靠性α。在水库调度期内，达到需求目标的概率，其计算公式为：

(14)

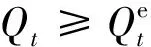
2) 可恢复性γ。在运行分析期内，水库从破坏状态恢复到正常供水的平均频率，其计算公式为：

(15)

式中：γ为水库供水可恢复性。

3) 缺水深度ν。水库运行分析期内，单个时段内的最大相对缺水量，其计算公式为：

ν=max{DR1,DR2,…,DRT}

(16)

4) 缺水指数MSI。反映水库供水效益的损失程度。

(17)

式中：T为调度期总时段数。

4 实例计算与分析

4.1 典型年的选择

选取1950—2018年共69年的水文序列，将其进行排频计算，然后根据Pearson-Ⅲ型曲线对水库年平均流量进行适线，选取P=5%为特丰水年，P=25%为较丰水年，P=50%为平水年，P=75%为较枯水年，P=90%为特枯水年。典型年的来水过程见图6。

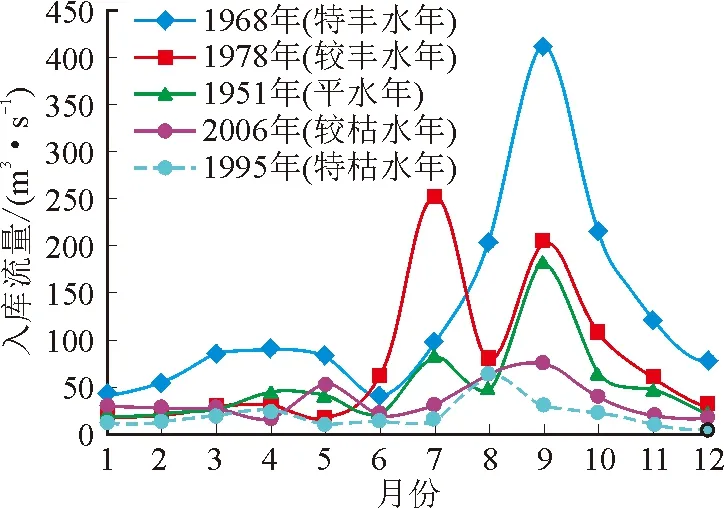
图6 林家村水库典型年入库流量Fig.6 Storage water of typical year of Linjiacun Reservoir

4.2 灌溉需水量计算

宝鸡峡水库的主要供水目标包括灌溉、发电和生态用水。根据文献[19]可知，特丰水年和较丰水年，渠首引水后下泄流量能够满足生态流量；平水年引水后生态流量不足；而较枯水年和特枯数年引水前生态基流已不足，引水后更加严重。故本文主要计算平水年、较枯水年和特枯水年的灌溉需水量。

根据宝鸡峡灌区的灌溉制度和灌溉定额，采用定额指标法，通过分析计算可以得到宝鸡峡塬上灌区的月灌溉需水量，结果见图7。其中50%典型年灌溉需水量为2.43亿m3，75%典型年灌溉需水量为5.55亿m3，90%典型年灌溉需水量为5.91亿m3。

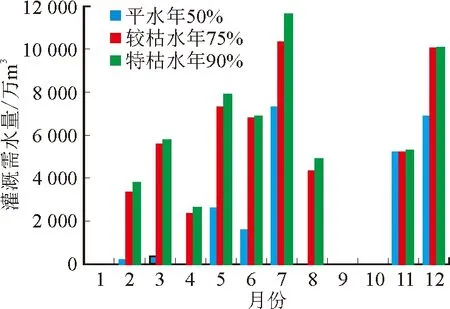
图7 不同典型年灌溉需水量Fig.7 Irrigation water requirement in different typical years

4.3 优化求解与结果分析

采用MATLAB编制水库生态调度的NSGA-Ⅱ-SEABODE优化求解算法，以月为调度时段，总调度时段12个，运行期为7月至次年6月。优化问题包括13个决策变量，分别是水库在12个时间段内的13个水位值(包括起始水位和结束水位)。选取种群规模N=100，最大迭代次数Gen=1 000，NSGA-II算法使用模拟的二进制交叉算子和多项式突变，交叉概率pc=0.9，变异概率pm=1/n，n是决策变量的个数，交叉分配指数ηc和突变分布指数ηm都是20。通过计算可得到100组Pareto最优解。不同典型年的优化调度结果见图8，可以看出灌溉效益与生态AAPFD值之间存在着竞争关系。为进一步分析优化结果，取其中的两种典型优化方案：方案1(生态AAPFD值最小)、方案2(灌溉效益最大)。当以追求灌溉效益最大为目标时，可选择方案2；当追求生态AAPFD值最小为目标时，可选择方案1。从方案1到方案2，水库的灌溉效益在增加的同时，生态AAPFD值也在增加。可见为了保障河道内具有一定的生态流量，会使水库的经济效益受到一定的影响。

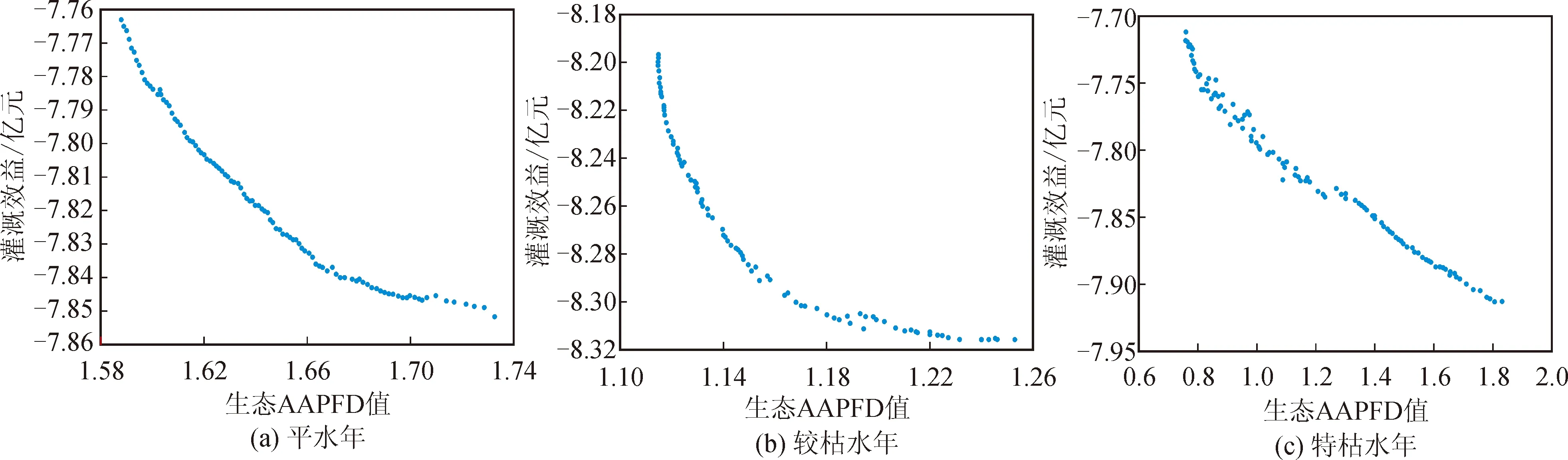
图8 不同典型年多目标Pareto散点图Fig.8 Pareto scatter diagram of multi-objective in different typical years

分别计算平水年、较枯水年和特枯水年水库属性空间C中4个评价指标值，统计结果见表3。

由表3可以看出，三个不同典型年中，不同方案的4个评价指标均存在差异。

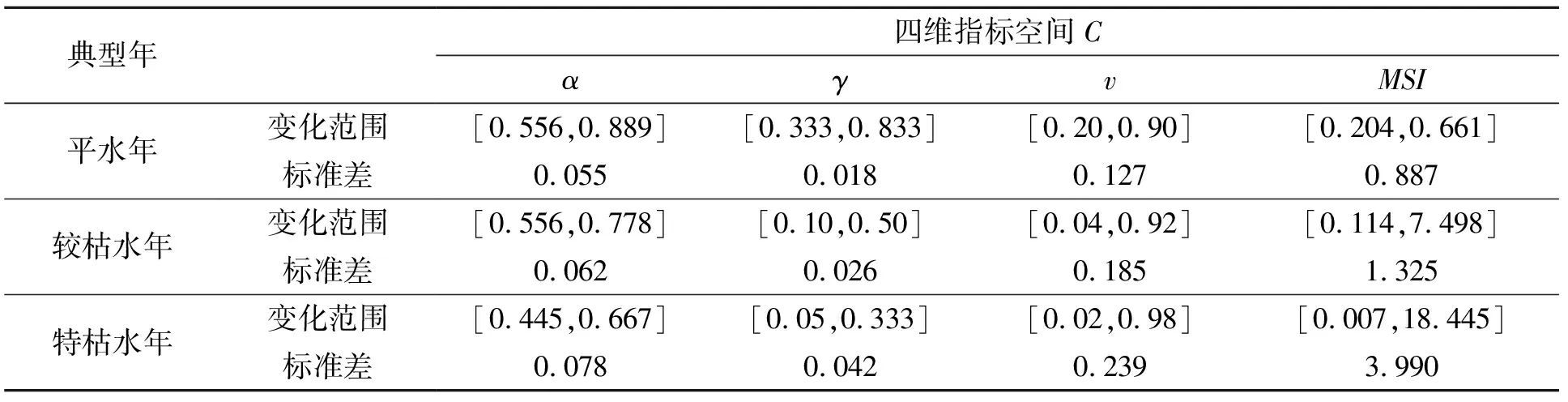
表3 决策空间A中不同典型年评价指标统计结果Tab.3 Statistical results of evaluation indicators of different typical years in decision space A

因此，可采用SEABODE法对方案集进行选择与淘汰，确定最终的偏好方案。

平水年、较枯水年、特枯水年三种典型年下，四维指标空间C及其三维子空间中的Pareto最优方案数统计结果见表4。

表4 不同典型年的指标空间C中Pareto最优方案个数Tab.4 Number of Pareto optimal schemes in indicator space C of different typical years

表4 不同典型年的指标空间C中Pareto最优方案个数Tab.4 Number of Pareto optimal schemes in indicator space C of different typical years

典型年(1234)(123)(124)(134)(234)三阶有效方案平水年4639301887较枯水年564229201513特枯水年49413613129

注：1-α，2-γ，3-ν，4-MSI。

在k=4的第一轮方案优劣排序识别中，不同典型年的方案A1～方案A100，在四维指标空间C中分别有46、56、49个方案是Pareto最优的，相当于偏好方案的优选范围分别缩小了54%、44%、51%。为了选择出一个具有代表性的偏好方案，需进一步完善和缩小决策者的选择范围。在第二轮中，将所选的四阶有效解进一步优化为三阶有效解，分别获得平水年的三阶有效方案个数是7个，较枯水年是13个，特枯水年是9个。第三轮k=2的方案优劣排序，同样使用SEABODE法进行优选，得到了平水年(P=50%)、较枯水年(P=75%)和特枯水年(P=90%)下，多属性决策的最终偏好方案分别为方案A29、方案A13、方案A80，结果见表5。

表5 典型年偏好方案结果Tab.5 Preference schemes for three typical years

从表5可以看出，不同典型年的生态调度性能评价指标差别很大。平水年的供水可靠性、可恢复性、脆弱性指标均优于较枯水年和特枯水年。其中，较枯水年和特枯水年的调水可靠性α分别下降了12.4 %、24.7%；可恢复性γ分别下降了25.4 %、50.7%；脆弱性ν分别下降了25.0%、33.3%。较枯水年的缺水指数MSI最小，为2.21，表明12月中有2个多月无法满足正常需水量。平水年、较枯水年、特枯水年的经济效益分别为7.949、8.452、7.927亿元，生态AAPFD值分别为1.624、1.207、1.425。

5 结 论

为解决水库生态调度模型构建和求解中存在的问题，本文提出并构建了一种耦合多目标相关分析、多目标优化和多属性决策的水库生态调度方法，并通过实例分析与验证可得出如下结论。

1) 通过抽取水库生态调度目标，并进行相关性分析，从而获得相互冲突的调度目标，使得水库生态调度模型的构建更具科学性和定量依据。

2) 将多目标优化和多属性决策方法结合，构建的NSGA-II-SEABODE算法，能够在优化求解模型的同时，从Pareto最优调度方案中优选出最终偏好调度方案。

3) 将建模方法、优化算法、优选方法耦合，从而为水库生态调度提供了一种贯通“模型构建-优化求解-方案优选”全过程的调度方法。