库区几何要素对溃坝洪水特性影响的模拟研究

黄子奇， 张建丰， 李 涛， 胡 晖， 高泽海， 杜佰林

(西安理工大学 西北旱区生态水利国家重点实验室， 陕西 西安 710048)

水坝溃决引起的洪水通常比暴雨引起的水文洪水更具破坏性，会对人民生命财产和国民经济造成极其严重的危害[1]。对溃坝洪水进行研究有助于人们计算分析溃坝洪水的危害，采取适当的预防措施。在其他科学研究中，溃坝波被用于模拟海啸波、风暴潮、涌潮等灾害，基于溃坝水流的缓蓄快放技术也被应用于景观水体水质的保持[2-3]。因此，对溃坝洪水的研究意义重大。

对溃坝洪水的理论研究可归结为求解Saint-Venant方程组的Riemann问题，以精确描述溃坝水流运动规律。Ritter[4]提出了无限库区长度情况下干底矩形棱柱体河槽中瞬溃的解析解。Dressier[5]提出了考虑流动阻力的Ritter解。伍超等[6]用Riemann方程推导出平底无阻力无限长度U形棱柱体河道溃坝波的简化解。王立辉等[7]利用特征函数和Riemann函数建立了斜底河道瞬溃的解析解。这些研究都是控制方程在简化条件下的解析解，实际应用受到了限制，溃坝洪水的理论研究仍然非常重要。

物理模型实验能够校核溃坝波理论解，研究洪水演进特性、其影响范围以及流态，是研究溃坝洪水的重要方法。Lauber等[8-9]通过矩形水槽实验研究了下游无水情况下溃坝波在平底河道与斜底河道的演进规律，得出了下游最大水深、流速和水深分布的规律等水力特性。Pilotti等[10]研究了库区平面形状对溃坝洪水的影响，总结了库区形状对下游水深的影响以及经验公式的适用性。Hooshyaripor等[11]论证了水库横截面边坡坡度对溃坝洪水洪峰流量、峰现时间以及下游水深随时间演变的重要作用。刘文军等[12]对上下游初始水深比为0～0.9时的瞬时溃坝水流进行了系统研究，分析了瞬溃洪水的运动特性并对湿底情况下溃坝水流的相似性进行了分析。目前的研究对库区宽度、长度等几何因素对溃坝洪水的影响关注较少，且关注点多集中在各断面水深过程的分析。

随着计算机技术的快速发展，通过数学模型模拟分析复杂流场成为研究热点，与物理模型相比，具有造价低、容易调整实验条件、能避免外界因素干扰等优点[13]。BRDAM、BREACH、DAMBREAK、BEED等模型已用于简单溃坝问题的计算[14]。夏军强等[15]建立了基于无结构三角网格下采用有限体积法求解的二维水动力学模型，用于模拟溃坝洪水在复杂边界及实际地形上的流动过程。胡晖等[16]利用MIKE 3 FM与Flow-3D对溃坝洪水进行数值模拟，与实测实验数据和解析解比较，研究了两种软件的适用性，得出了MIKE 3 FM模型适用于大型区域中实际溃坝问题的计算，Flow-3D模型适用于精细计算。坝址是上、下游的连接点，使用数值解法研究溃坝洪水时被作为下游的边界条件使用，准确推求坝址断面流量过程线非常重要，然而在实际工程中，坝址断面流量过程线多通过概化算法获得，一般默认溃坝开启的时刻即为坝址峰现时间。使用Flow-3D进行数值模拟获得的坝址断面流量过程线包含流量增大至洪峰流量的过程，与概化算法相比有一定的优势。

现有研究缺乏针对库区宽度、长度等几何因素对溃坝洪水特性影响的关注，且实验分析较少涉及流量和波速。本文应用Flow-3D构建水槽的数值模型，提出了获取物理水槽实验流量数据的方法，通过物理模型实验流量数据验证了数值模型的合理性，通过数值模型研究库区蓄水深度hu、库区宽度B、库区长度L对坝址断面流量过程、溃坝洪水水面线、溃坝洪水洪峰流量、峰现时间、溃坝波波速等特性的影响，对溃坝洪水的模型实验作出一定的补充。

1 实验工具和方法

物理模型实验在西安理工大学露天试验场的矩形棱柱体水槽内进行，实验时间是2018年5月中旬。水槽形式见图1，水槽以有机玻璃制成，底坡为0.002 5，糙率为0.01，宽0.3 m，高0.3 m，长10.8 m，距上游边界2 m处设置一块平板闸门将水槽分为上游蓄水库区与下游河道，即上游蓄水库区长度为2 m。坝址(闸门)上游设置10个观测断面，坝址下游设置6个观测断面，坝址处设置1个观测断面，以坝址为原点，溃坝洪水向坝址下游传播为正方向建立数轴，各监测断面的坐标见表1。

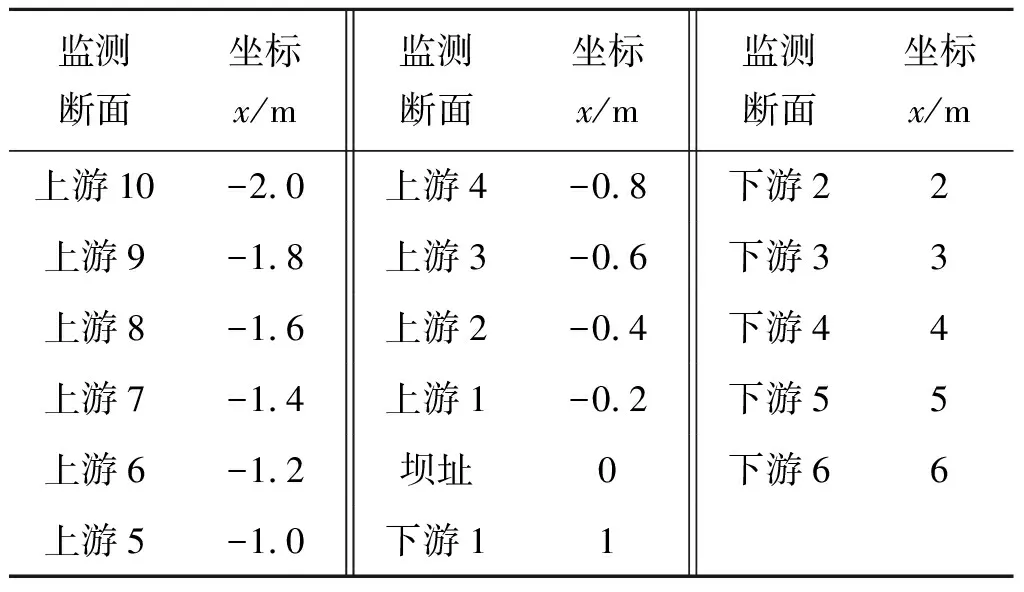
表1 监测断面坐标

进行实验时，其无量纲化闸门提升时间为(g/hu)1/2t<21/2，满足瞬间溃坝条件(g为重力加速度，取9.8 m/s2；hu为库区蓄水深度，m)[8]。

实验水深数据采用录像法获得。使用高速相机对准观测断面，调节焦距使观测断面的水深刻度与秒表在拍摄范围内清晰可见，录像速度为30 fps，开始录像后，在快速打开闸门的同时按下秒表计时按键，待观测断面处水位不再变化时停止录像。按帧查看视频即可获得观测断面的水深随时间变化的过程，按相同时刻汇总17个观测断面的水深即可获得不同时刻的水面线变化情况。实验中对每个工况都重复3次进行，水深数据取3次实验的平均值得到。

由于流量数据无法直接测得，本文根据相邻两时刻水面线与边界围成的水体体积变化进行推求，计算公式为：

(1)

式中：Δt为时间间隔；V(t)为t时刻观测断面与水槽边界、观测断面上游的水面围成的水体体积；Q(t+Δt/2)为t+Δt/2时刻观测断面的流量。

2 数学模型

2.1 公式和数学符号

在溃坝洪水数值模拟中，一般不考虑水流压缩性， Flow-3D采用如下方程控制流体运动。

连续性方程：

(2)

动量方程：

(3)

紊流模型采用采用RNGk-ε模型，其k、ε方程见下。

k方程：

(4)

紊动耗散率ε方程：

(5)

(6)

(7)

(8)

(9)

(10)

式中：ui、uj为流速分量，i、j= 1，2，3；xi、xj为坐标分量；ρ为体积分数平均密度；μ为流体动力黏滞系数，μt为流体湍动黏度；P为作用在流体微元上的压力；k为紊动能；Gk为由于流速梯度引起的紊动能产生项；ε为紊动能耗散率；η为紊动时间与应变尺度的比值；Eij为时均应变率；本研究取Cμ、Cε1、Cε2、σk、σε、η0、β等经验常数为软件默认值。

Flow-3D采用流体体积法(VOF)追踪模型沿程自由液面变化。VOF的基本原理是通过研究网格单元中流体和网格体积比函数F来构造和追踪自由液面[17]。若F=1，则该单元全部为液体所占据；若F=0，则该单元为无液体单元；当0

(11)

式中参变量含义同上。

Flow-3D采用有限差分法通过将模型和计算域独立进行网格生成，将方程离散从而转化为代数方程组并进行数值求解。其独特的Favor网格处理技术对三维实体做六面体划分，能够消除和顺滑不平整区域，可解决网格模型失真问题。

2.2 模型建立

本研究利用Flow-3D按照物理模型的形式构建数值模型，具体参数见表2。利用工况1、2、3可对比分析库区蓄水深度hu对溃坝洪水的影响，利用工况3、4、5可对比分析库区宽度B对溃坝洪水的影响，利用工况3、6、7可对比分析库区长度L对溃坝洪水的影响。工况4与工况6的库容相同，工况5与工况7的库容相同，对比这些工况可知库区长度与宽度对溃坝洪水水力要素作用的差异。综合考虑求解精度与收敛速度，模型的网格尺寸设置为5 mm。

表2 数值模型参数Tab.2 Parameters of the numerical model

2.3 模型验证

为了验证数值模型的准确性，本文将物理模型实验与数值模拟结果进行对比。选取坝址上游距离坝址1 m处的断面、坝址断面、坝址下游距离坝址3 m 处的断面对比数学模型与物理模型的水深、流量随时间变化的过程，结果见图2。观察得出，在库区蓄水深度为9 cm的工况下，将闸门快速提起，河道水体的突然外泄，闸门附近水位迅速下降，形成洪水波向下游演进。当洪水波传播至某一断面，该断面水深快速升高，一段时间后水位逐渐下降，Flow-3D模拟的结果与观测结果吻合。其中，图2(c)中下游断面0 s至3 s时间内水深不为0，是因为闸门有少量漏水。上游断面、坝址断面、下游断面水深数据的相对误差分别为6.66%、9.11%、9.88%，流量数据的相对误差分别为9.85%、10.63%、10.23%，说明模型模拟精度基本满足要求，本研究采用的数值模拟方法合理，可用于溃坝洪水的模拟研究。

图2 各断面水深、流量变化Fig.2 Depth and discharge change for each section

3 模拟结果分析

3.1 坝址断面流量过程

图3为各种工况下的坝址流量过程线。闸门瞬间移除时，产生引起水位上升的正波向坝址下游传播、引起水位下降的负波向坝址上游传播。由于此时上下游水位差最大，坝址断面瞬间到达最大流量。随着洪水向坝址下游演进，坝址上游水位降低，流量随之减小。待上游水位基本稳定后，上下游水位差将在一段时间内保持稳定，流量也保持稳定。一段时间后，上下游水位差不断减小，流量随之减小，直到上下游水位相等时，流量减小为零。

图3 坝址断面流量过程线(x=0)Fig.3 Discharge process in damsite(x=0)

工况1、2、3的峰现时间分别是0.12 s、0.14 s、0.16 s，洪峰流量分别为0.046 m3/s，0.071 m3/s，0.099 m3/s。0～5 s之间有一个流量基本不变的稳定阶段，其流量稳定时间约为2.69 s、1.97 s、1.60 s，稳定流量约为0.039 m3/s、0.060 m3/s、0.083 m3/s。可见随着库区蓄水深度的增加，坝址处洪峰流量增大，峰现时间推迟，流量稳定持续时间减少，稳定流量增大。

工况3、4、5的洪峰流量分别为0.099 m3/s，0.132 m3/s，0.165 m3/s，峰现时间均是0.16 s。流量稳定时间约为1.60 s、1.59 s、1.61 s，稳定流量约为0.083 m3/s、0.111 m3/s、0.139 m3/s。可见，随着库区宽度的增加，坝址处洪峰流量增大，峰现时间基本不变，流量稳定持续时间基本不变，稳定流量增大。

工况3、6、7的洪峰流量均为0.099 m3/s，峰现时间均为0.16 s，流量稳定时间约为1.60 s、2.43 s、3.36 s，稳定流量约为0.083 m3/s。可见，随着库区长度的增加，洪峰流量、峰现时间均不变，流量稳定持续时间增长，稳定流量不变。

根据Ritter解的坝址洪峰流量公式，坝址洪峰流量与库区宽度、库区蓄水深度成正比，与库区长度无关，与本研究相符。库区长度的变化对坝址断面的峰现时间没有影响，与稳定流量的持续时间成正比。各种工况下，稳定流量均为洪峰流量的8/9，此时对应的水深为库区蓄水深度的4/9，根据Ritter解，坝址断面将会长久维持在这一水深，研究结果与Ritter解不同的主要原因是Ritter解的基本假定是库区拥有无限长度，而本研究是基于有限长度的水槽实验，因此在一段时间后，流量与水深均会下降，这也说明了本研究的合理性[4]。

3.2 溃坝洪水水面线

图4为不同工况下坝址下游水面线。随着库区蓄水深度的增加，溃坝波附加比降增大，各断面最大水深逐渐增大(图4(a))。随着库区宽度的增大，水面线基本重合，溃坝波附加比降和各断面最大水深基本不变(图4(b))。随着库区长度的增大，各断面最大水深增大，库区长度与达到最大水深时间成正比。溃坝洪水向下游演进的初始阶段，较小的库区长度达到最大水深之前水面线基本重合，溃坝波附加比降基本不变。之后水面线逐渐下降，与其他工况的水面线偏离，其他工况的水面线仍然重合。随着溃坝洪水向下游演进，溃坝波附加比降逐渐变缓，沿程各断面最大水深逐渐降低，这是由于河道具有调蓄作用，溃坝波在传播的过程中将逐渐坦化。

图4 溃坝洪水水面线Fig.4 Dam-break flood water surface profile

3.3 洪峰流量

图5为各断面洪峰流量。随着库区蓄水深度、库区长度的增加，沿程各断面洪峰流量Qm均增大；随着库区宽度的增大，各断面洪峰流量均增大。

图5 各断面洪峰流量Fig.5 Peak discharge in each section

为了说明库区蓄水深度、库区宽度、库区长度对溃坝洪水洪峰减小的影响，用各断面洪峰流量与坝址断面洪峰流量的比值来表示，即为α，各工况下各断面α值见表3。由工况1～5的α值可知，随着库区蓄水深度与库区宽度的增大，沿程各断面α基本不变，即库区蓄水深度与库区宽度的变化对下游的洪峰减小没有影响。对比工况3与工况7，库区长度由3 m增大到5 m，沿程各断面α平均增加了8.2%，说明库区长度的增大均对溃坝洪水的洪峰减小有抑制作用。

表3 不同工况下各断面α值Tab.3 α value of each section under different conditions

3.4 各断面波前到达时间

图6为各断面波前到达时间。随着库区蓄水深度的增加，各断面的波前到达时间t1均明显提前。随着库区宽度或长度的增加，各断面的波前到达时间基本不变。说明溃坝波波速只与库区蓄水深度有关，Ritter的研究结果与此相似[4]。主要原因是，水体流动是因为单位重量水体的位能与压能转化为动能，位能和压能只与水深有关，与库区长度和宽度无关。

图6 各断面波前到达时间Fig.6 Wave front arrival time in each section

见图3，随着库区蓄水深度的增加，坝址断面的流量过程线的稳定时间缩短，库区宽度的变化对稳定时间基本没有影响。随着库区长度的增加，稳定时间增长，主要原因是负波到达水槽上边界，被反射再传播至坝址断面的过程流量保持稳定，之后再逐渐减小，库区长度越大则负波的传播距离越长，流量保持稳定时间延长。库区蓄水深度增大使波速增大，导致流量稳定时间缩短，库区宽度对波速与传播距离均没有影响，因此稳定时间基本不变。

3.5 各断面峰现时间

图7为沿程各断面的峰现时间。各种工况下，随着溃坝波的传播，沿程各断面峰现时间t2逐渐推迟。随着库区蓄水深度的增大，各断面峰现时间均提前，随着库区长度的增大，各断面峰现时间均推迟，库区宽度的变化对各断面峰现时间基本没有影响。工况4、5的峰现时间明显迟于工况6、7，即库容相同时，库区长度较大水库各断面的峰现时间较迟。

图7 各断面峰现时间Fig.7 Time to peak in each section

不同库区长度工况下，同一时刻波前所在位置相同，溃坝波的附加比降i相同(图4(c))。随着库区长度的增加，各断面最大水深增大，即波峰高度增大(图4(c))。溃坝波波前到波峰的水平距离增加(l=h/i)。库区长度不同的工况下，沿程各断面波前到达时间相同，峰现时间不同，主要原因是在波速v相等的情况下(图6(c))，波峰到达时间将推迟(t=l/v)。

靠近坝址的断面，由于洪水水头大，传播速度快，属于高风险区。根据对各断面洪峰流量的研究结果，库区长度较大时，靠近坝址断面的洪峰流量仅以较小的幅度增大。对于这些断面，溃坝洪水的危害基本没有加剧或小幅度地加剧，但峰现时间的推迟，使溃坝洪水发生时，人民财产有了更充裕的转移时间，这降低了溃坝洪水的危害，有利于溃坝风险的管理。

4 结 论

1) Flow-3D对溃坝洪水的模拟结果与理论研究相符合，与物理实验实测数据误差较小，并且比人工推求洪水过程更加精细，能够广泛使用。

2) 增加库区蓄水深度hu，坝址及沿程各断面洪峰流量增大，峰现时间提前，溃坝洪水对下游的危害加剧，溃坝波波速增大。

3) 增加库区宽度B，坝址及沿程断面洪峰流量增大，各断面峰现时间均不变，溃坝洪水对下游的危害不变，溃坝波波速基本不变。

4) 增加库区长度L，坝址断面洪峰流量不变，沿程各断面洪峰流量以较小幅度增大，坝址断面峰现时间不变，沿程各断面峰现时间推迟，溃坝波波速不受影响。

综合来看，通过增加库区蓄水深度hu来增大库容，会加剧溃坝洪水对下游的危害。库区长度较大的水库，有利于溃坝发生时下游人民财产的转移，降低了溃坝洪水的危害。而库区宽度基本不影响溃坝洪水对下游的危害。本研究对建造水库的工程设计以及溃坝风险管理具有指导意义。