基于不同坡比的黄土边坡大雨降雨入渗测试与比较

关晓迪， 李荣建， 潘俊义， 孙 萍， 姚夷凡

(1. 西安理工大学 岩土工程研究所， 陕西 西安 710048； 2. 西安长庆科技工程有限责任公司， 陕西 西安 710018；3. 中国地质科学院 地质力学研究所，北京 100081)

黄土，一种第四纪沉积物，广泛分布于美国、俄罗斯、新西兰和中国等地区[1-3]，约占世界面积的2.5%[4]。其中，中国黄土主要分布于西北地区，面积约6.4×105km2，具有沉积最广、地层最全、厚度最大的特征[5-6],加之黄土特殊的结构性和水敏性，降雨是黄土边坡失稳变形和破坏的主要诱因之一[7-9]。

在现场试验研究方面，胡明鉴等[10]开展了人工降雨的滑坡泥石流现场试验，初步揭示了蒋家沟地区暴雨-滑坡-泥石流的共生关系。武红娟等[11]针对不同坡比的公路路堑边坡开展了现场模拟降雨的边坡冲刷试验，研究了黄土边坡抗冲刷的最优坡比问题。简文星等[12]在黄土滑坡1#崩塌体上进行了双环渗透试验与降雨现场监测，获取了改进的入渗模型参数。王磊等[13]开展了人工模拟降雨现场试验，通过隔离边界设置真实再现了人工降雨时雨水入渗对边坡开裂的影响过程。

然而，现场试验成本高、难操作，试验结果常常差强人意，而模型试验不受外界和自然条件的限制，试验结果精准，且节省人力、资金和时间，因此被广泛应用于各种土工问题中[14]。李焕强等[15]通过粉砂边坡模型，采用自动水分传感器测定含水率，用光纤传感器测定应变，研究了降雨入渗作用下边坡性状的变化规律。钱纪芸等[16]通过粉质黏土边坡降雨的离心模型试验，分析了边坡位移对降雨入渗的响应规律。詹良通等[17]通过离心机模拟了不同雨强下非饱和粉土边坡的失稳过程，得到了雨强与边坡失稳的时间关系曲线。江强强等[18]开展了降雨和库水位联合作用下库区岩土质边坡模型试验研究，揭示了三峡库区滑坡的演化规律及孕灾机制。

上述模型、试验研究成果有效推动了边坡降雨入渗研究的发展，但还缺乏不同坡比条件下针对均质黄土边坡降雨入渗规律的系统研究。因此，本文以甘肃庆阳地区高4 m的黄土边坡为原型，根据相似原理，建立室内黄土边坡模型，模拟大雨条件下3种坡比的边坡降雨入渗，对比分析不同坡比的入渗特征及坡面冲刷规律。研究结果可为西北地区自然黄土边坡的防护和降雨型滑坡的治理提供一些建设性意见。

1 模型边坡降雨入渗试验

1.1 试验相似比尺

本试验原型边坡坡高4 m，宽2.5 m，考虑到室内场地的限制，将原型与模型边坡的几何相似比设定为Cl= 4，并在设计渗透模型试验时抓住主要因素，使原型与模型土的渗透系数相似比严格满足Ck= 2，略微放松次要因素，使干密度的相似比近似满足Cρ= 1，以降低模型边坡的制样难度。由此，采用量纲分析理论和相似准则，推导出原型与模型的降雨相关各物理量的相似关系，如表1所示，原型与模型黄土的物性指标如表2所示。

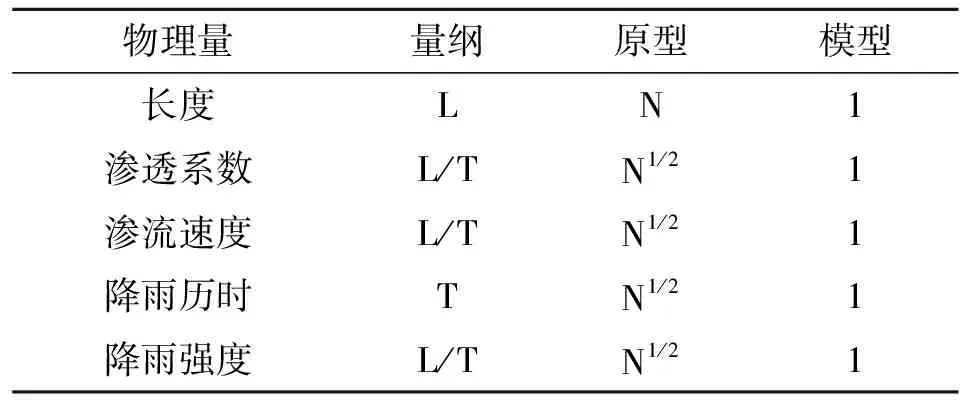
表1 降雨相关各物理量的相似比尺Tab.1 Similar scale of physical quantities related to rainfall

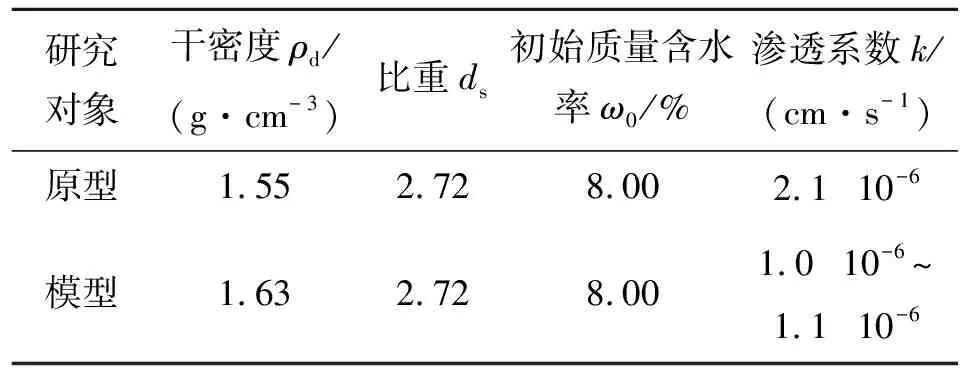
表2 原型和模型黄土物性指标Tab.2 Loess physical properties of prototype and model

1.2 试验装置

试验设备由边坡模型箱、降雨系统和监测系统组成。降雨系统主要包括一体式实心锥形喷头、PPR降雨管路和降雨支架等，锥形喷头可通过旋转喷嘴来调整喷洒效果，降雨均匀度达85%以上。监测系统对含水率、基质吸力、湿润锋及坡面冲刷进行监测。模型试验原理如图1所示。

图1 模型试验示意图Fig.1 Schematic diagram of the model test

1.3 试验方案

本试验基于3种坡比(坡比1∶1、1∶0.75和1∶0.5)的边坡，开展了大雨条件下持续降雨24 h的模型边坡降雨试验，其中降雨强度为10.75 mm/d。不同坡比的边坡传感器埋深如图2所示，在边坡不同位置和深度布置了10个水分传感器、3个张力计，Wn表示水分传感器，Sn表示张力计。

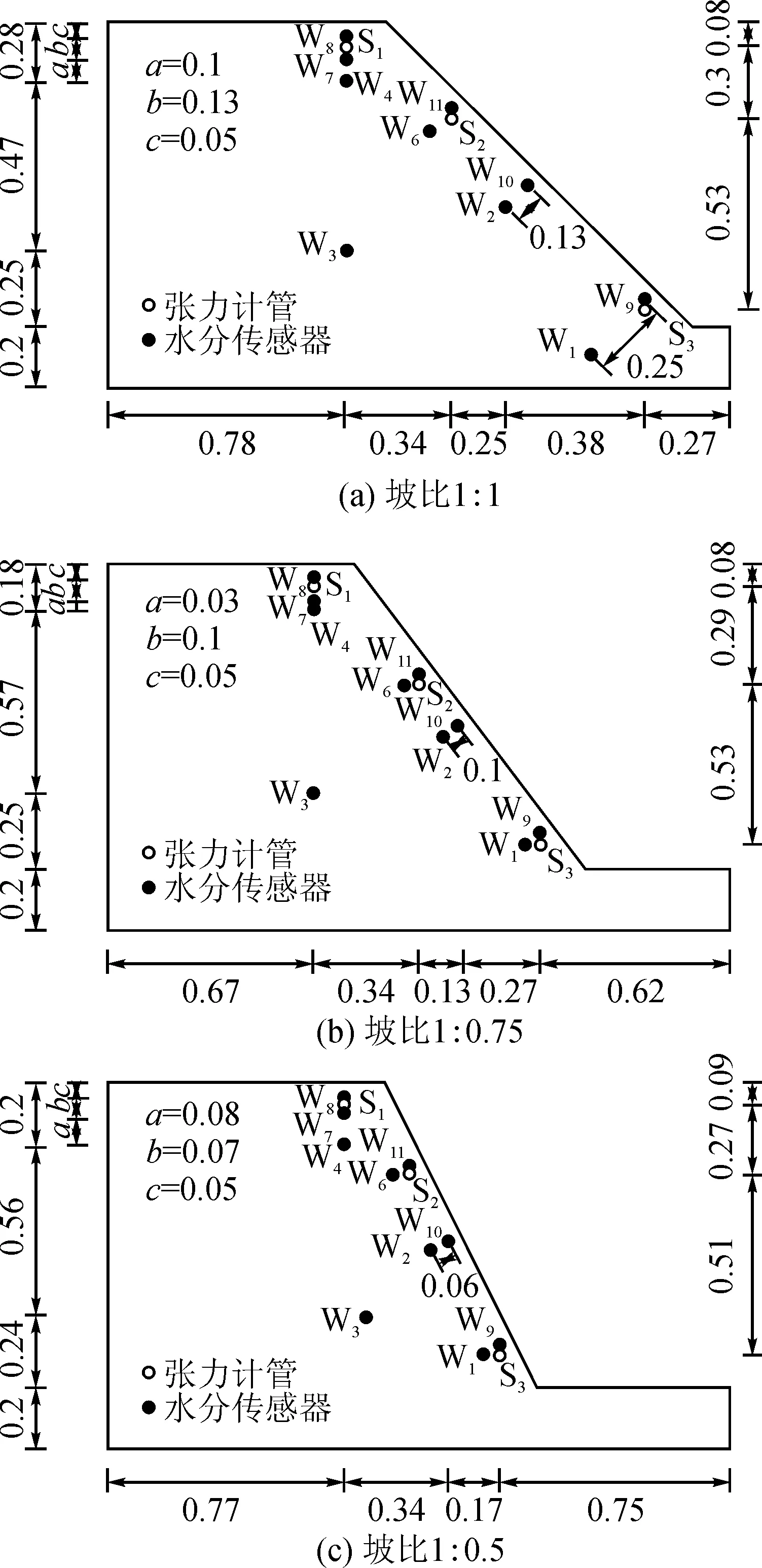
图2 传感器埋设图(单位：m)Fig.2 Sensor embedding diagram(unit:m)

2 试验结果与分析

2.1 不同坡比对体积含水率的影响分析

图3为边坡降雨过程中不同坡比的体积含水率时程曲线。由图可知： 降雨过程中测点W3含水率均未发生变化，说明坡面入渗深度小于75 cm；距坡面同为5 cm深度的坡顶测点W8、坡脚测点W9、坡中测点W11处含水率增长速率递减，说明坡顶降雨入渗速率最快、坡脚较快、坡中最慢，且测点W11、W8、W9处含水率峰值依次递增，说明坡脚入渗最深、坡顶较深、坡中最浅[19]；降雨24 h后，测点W11、W8、W9处含水率曲线变化平缓，略微呈现负增长，这是由于降雨结束后蒸发作用使含水率减小；距坡顶不同深度处的测点W4含水率先开始增长，然后是测点W7、最后是W8，且相应的含水率增长速率递增，说明雨水的入渗能力随着降雨入渗深度的增加而减弱。

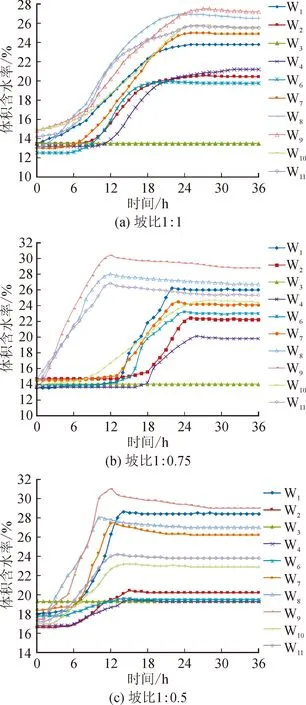
图3 不同坡比含水率的时程曲线Fig.3 Time-history curves of moisture content at different slope ratios

不同坡比的边坡在同一测点W9或W11处其含水率的突变速率和峰值不同，其中坡比1∶1的边坡在W9处含水率峰值为27.5%、W11处含水率峰值为25.7%；坡比1∶0.75的边坡在W9处含水率峰值为29.5%、W11处含水率峰值为25.5%；坡比1∶0.5的边坡在W9处含水率峰值为31%、W11处含水率峰值为24.2%。本文以坡比1∶1边坡作为参照条件，定义了W9和W11处含水率峰值的相对变化率(式(1))，得到了坡比1∶0.75、1∶0.5条件下，W9处含水率分别增大了7.3%、12.7%，W11处含水率分别减小了0.8%、5.8%，且坡比越大的边坡，W9处含水率曲线越陡，W11处含水率曲线越缓，呈现出坡比越大，坡脚含水率突变速率越快且峰值越高，坡中突变速率越慢且峰值越低的特点，表明坡比越大，坡脚降雨入渗速率越大，坡中入渗速率越小。这是由于坡脚以零度角平面接受雨水，坡中则存在一定角度，而角度无形中削弱了雨强。同时，不同坡比的边坡降雨入渗深度不同，坡比1∶1的边坡坡顶降雨入渗深度28～75 cm，坡中18～75 cm，坡脚30～75 cm；坡比1∶0.75的边坡坡顶入渗深度20～75 cm，坡中15～30 cm，坡脚15～75 cm；坡比1∶0.5的边坡坡顶入渗深度20～75 cm，坡中11～30 cm，坡脚11～75 cm。说明降雨入渗深度呈现出坡脚最深、坡顶较深、坡中最浅的特点，且坡比越大，坡中降雨入渗深度越浅，这是由于随着降雨的持续，坡面表层土体入渗能力降低，当降雨强度大于土体入渗能力时，坡面开始产生径流，且坡比越大的边坡径流现象越明显，坡中降雨入渗程度越差。

nθ=(θa-θ0)/θ0×100%

(1)

式中：nθ为含水率峰值的相对变化率；θa为坡比1∶0.75(或1∶0.5)边坡的体积含水率，%；θ0为坡比1∶1边坡的体积含水率，%。

2.2 不同坡比对基质吸力的影响分析

图4为不同坡比的边坡在测点S1、S2、S3处的基质吸力时程曲线。由图可知： 降雨过程中，不同坡比的边坡坡顶处基质吸力变化情况基本相同，基质吸力值稳定在21 kPa附近；持续降雨5～6 h，坡顶、坡中及坡脚的基质吸力均开始减小，持续降雨6～12 h，坡顶、坡中及坡脚的基质吸力变化均较为明显，且坡比1∶1边坡的坡中基质吸力曲线最陡，坡比1∶0.75和1∶0.5的坡中基质吸力曲线依次变缓，说明坡比1∶1边坡的坡中基质吸力减小速率最快，坡比1∶0.75次之、坡比1∶0.5最慢；同时，坡比1∶0.5边坡的坡脚基质吸力减小速率最快，坡比1∶0.75次之，坡比1∶1最慢，表明坡比越大，坡脚降雨入渗速率越快，坡中入渗速率越慢；降雨至12 h左右，坡比1∶1边坡的坡中基质吸力最先达到稳定值，坡比1∶0.75次之，坡比1∶0.5最慢，且坡中处的基质吸力稳定值分别为23 kPa、26.3 kPa、27.8 kPa。本文以坡比1∶1边坡作为参照条件，定义了坡中处基质吸力稳定值的相对变化率(式(2))，得到了坡比1∶0.75、1∶0.5条件下，坡中基质吸力稳定值分别增大了14.3%、20.9%，说明坡比越小，坡中基质吸力稳定值越小，降雨入渗越充分。随着降雨的持续，坡中基质吸力虽略有起伏，但总体趋势较为平稳。

图4 不同坡比基质吸力的时程曲线Fig.4 Time-history curves of matric suction at different slope ratios

nj=(ja-j0)/j0×100%

(2)

式中：nj为基质吸力稳定值的相对变化率；ja为坡比1∶0.75(或1∶0.5)边坡的基质吸力稳定值，kPa；j0为坡比1∶1边坡的基质吸力稳定值，kPa。

2.3 不同坡比对湿润锋的影响分析

图5为持续降雨24 h后不同坡比边坡的湿润锋。由图可看出： 不同坡比的边坡在坡中位置处湿润锋深度差异明显，坡比1∶1边坡坡中湿润锋深度范围为20～25 cm、坡比1∶0.75边坡坡中湿润锋深度范围为15～20 cm、坡比1∶0.5边坡坡中湿润锋深度范围为10～15 cm，以坡比1∶1边坡的坡中湿润锋深度作为参照条件，坡比1∶0.75湿润锋深度减小5～10 cm，坡比1∶0.5湿润锋深度减小10～15 cm，说明坡比越大，坡中降雨入渗深度越浅。这是由于随着坡比的增大，边坡坡中处接受雨水的能力减弱，持续降雨至坡面开始产生径流时，坡比越大，坡面径流越明显，坡中入渗程度越差，入渗深度越浅。

图5 不同坡比湿润锋Fig.5 Wetting front of the slope at different slope ratios

2.4 不同坡比对边坡冲刷的影响分析

图6为不同坡比边坡的坡面冲刷效果图。由图可看出： 在降雨过程中，坡比1∶1的边坡坡面表层土体剥落，降雨至15 h左右，坡表土体饱和，坡面处可见沟状径流，本文通过地面产流计算公式(式(3))，得到了坡面产流的径流深约为3.89 mm，降雨结束后坡肩形成一道宽约2 cm、长约35 cm的冲蚀沟；降雨至14 h左右，坡比1∶0.75的边坡坡表土体达到饱和，坡面径流现象明显，且坡面产流径流深约为4.32 mm，表层土体在降雨侵蚀作用下形成了游离态的泥土，雨水携带着泥土呈条状沿坡面往下流，在坡脚堆积成松软淤泥层，坡肩处形成明显的冲蚀沟；坡比1∶0.5的边坡坡面土体剥落最为严重，降雨12 h左右，边坡表层土体逐渐饱和，坡面形成了较强的泥流运动，坡面产流径流深约为4.97 mm，靠近模型箱侧壁的坡面土体出现了多处冲刷凹坑，坡肩冲蚀沟发育程度最好，坡脚淤泥层加厚。本文以坡比1∶1边坡作为参照条件，定义了坡面产流径流深的相对变化率(式(4))，得到了坡比1∶0.75、1∶0.5条件下，坡面产流径流深分别增大了11.1%、27.7%。上述试验结果表明：坡比越大，坡面径流现象越明显，冲刷程度越剧烈，且坡脚堆积的淤泥层越厚。这可能是由于坡比越大，坡面土体的入渗能力越弱，坡面雨水往坡脚流动的趋势越强，坡面遭受雨水侵蚀的程度越严重。

图6 不同坡比的坡面冲刷现象Fig.6 Slope scour phenomena at different slope ratios

(3)

式中：R为径流深，mm；Δt为计算时段，h；Q为单位时间的流量值，cm3/s；F为径流面积，m2；3.6为单位换算系数。

nR=(Ra-R0)/R0×100%

(4)

式中：nR为坡面产流径流深的相对变化率；Ra为坡比1∶0.75(或1∶0.5)边坡的坡面产流，mm；R0为坡比1∶1边坡的坡面产流，mm。

3 边坡降雨的渗流分析

3.1 数值模型建立

采用Geo-studio软件建立相应的数值模型来分析边坡降雨入渗规律，数值模型网格划分如图7所示。设置降雨条件为边界条件，以降雨强度的方式作用于边坡上表面，日降雨量为2.07×10-9m·s-1，降雨时长为24 h。设置模型底面为零压力线。

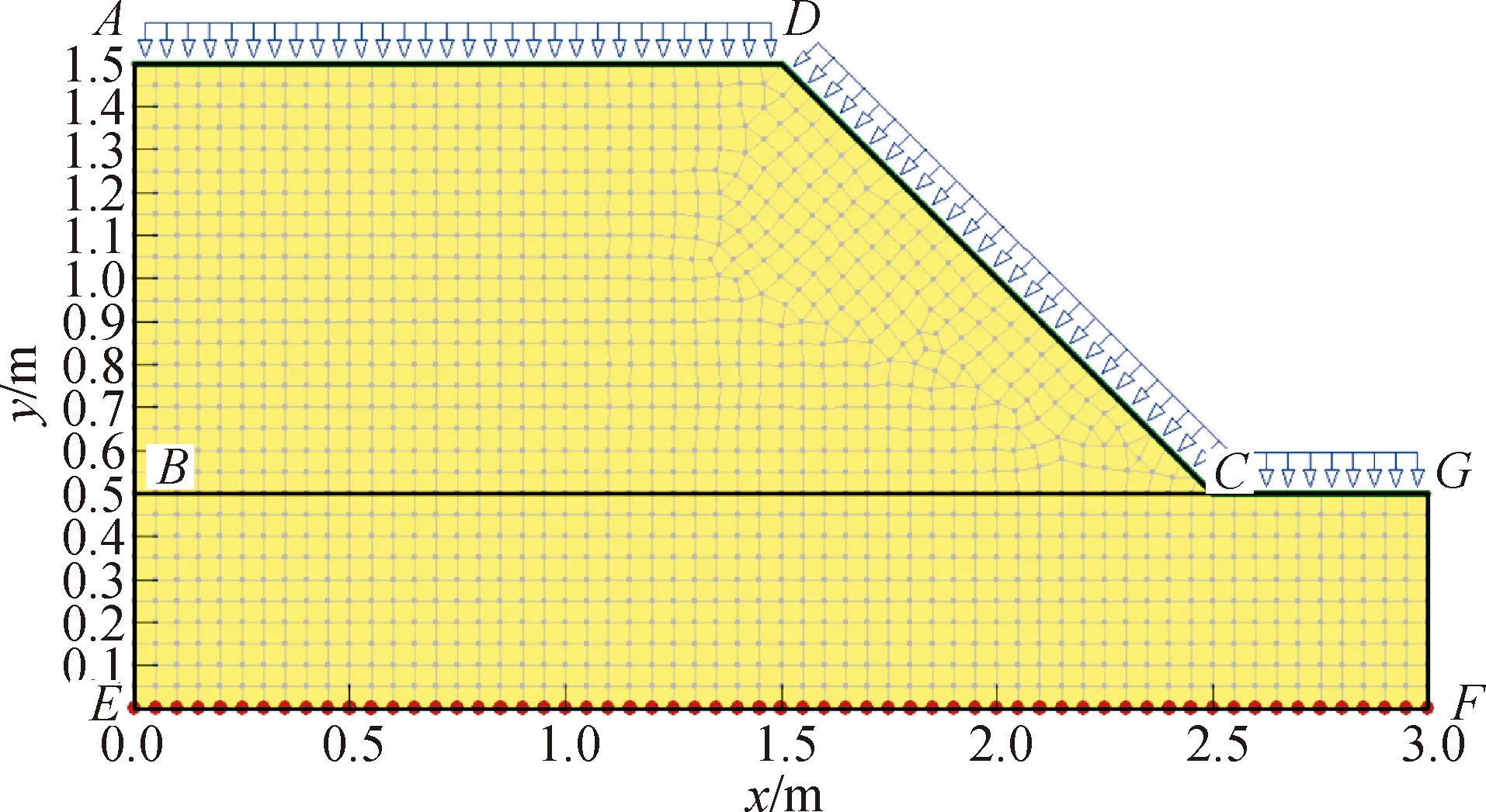
图7 网格划分及边界条件设置示意图Fig.7 Schematic diagram of grid division and boundary condition setting

3.2 数值模型参数

黄土的初始体积含水率为12.4%，数值模拟中，取a=20 kPa、n=2、m=0.5，运用V-G模型，可得黄土的土-水特征曲线，如图8所示。渗透系数与基质吸力的关系如图9所示。

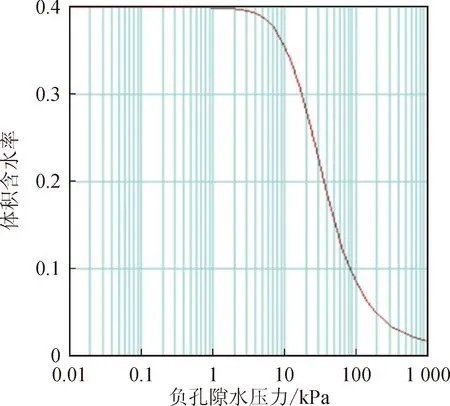
图8 土-水特征曲线Fig.8 Soil-water characteristic curve

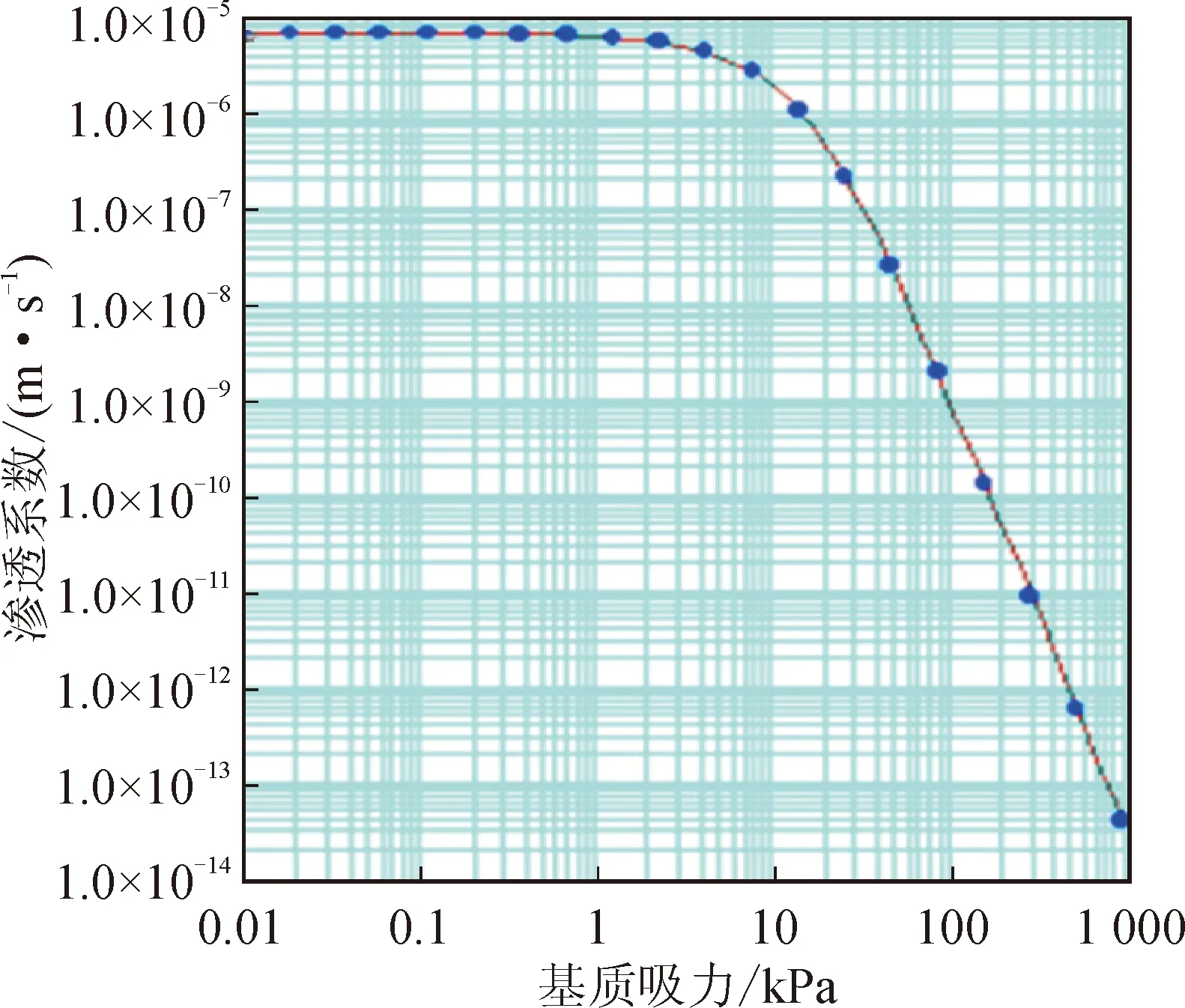
图9 渗透系数与基质吸力关系曲线Fig.9 Relationship between permeability coefficient and matric suction

3.3 模拟结果分析

坡比1∶1边坡的初始状态体积含水率分布如图10所示。由图可知，各土层的含水率自上而下逐级递增，表层含水率在12%左右，基层为13.4%。

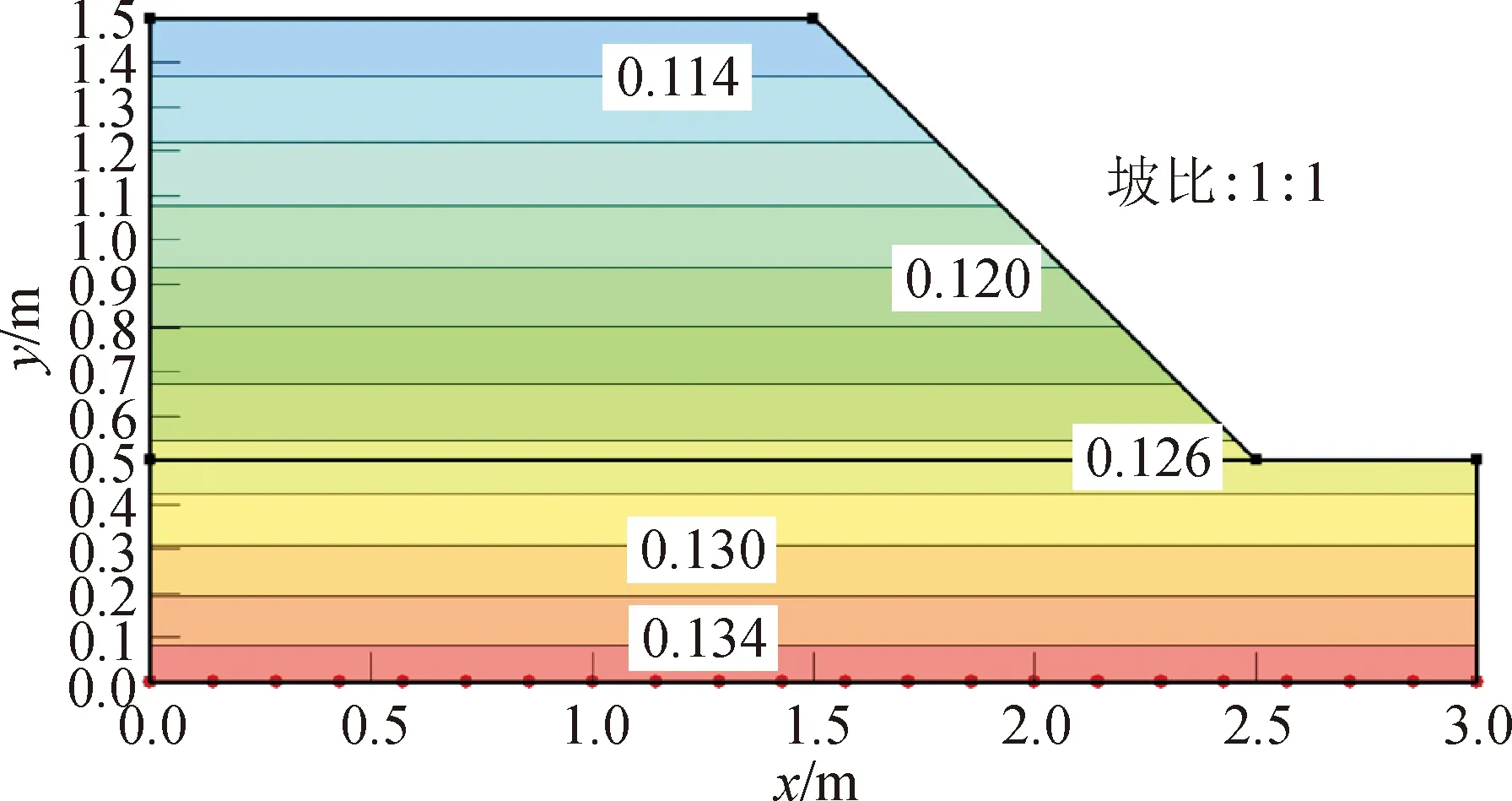
图10 初始时刻含水率分布图Fig.10 Moisture content distribution diagram at initial time

图11为降雨6 h不同坡比边坡的体积含水率分布图。由图可知： 降雨6 h时左右，不同坡比边坡的坡面表层含水率等值线均变得密集，坡顶表层含水率相差不大，都在13%左右，坡比1∶1、1∶0.75和1∶0.5的边坡坡中表层含水率分别为13%、12.5%和12%，同初始状态的12%相比，坡比1∶1含水率增加1%，坡比1∶0.75含水率增加0.5%，可见坡比越大，坡中含水率变化量越小，变化速率越慢，说明坡比越大，坡中降雨入渗速率越慢，入渗深度越浅。坡比1∶1、1∶0.75和1∶0.5的边坡坡脚表层含水率分别为14%、14.5%、15%，同初始状态的12.6%相比，坡比1∶1含水率增加1.4%，坡比1∶0.75含水率增加1.9%，坡比1∶0.5含水率增加2.4%，可见坡比越大，坡脚含水率变化量越大，变化速率越快，说明坡比越大，坡脚降雨入渗速率越快，入渗深度越深。这与室内边坡模型试验的结论一致。

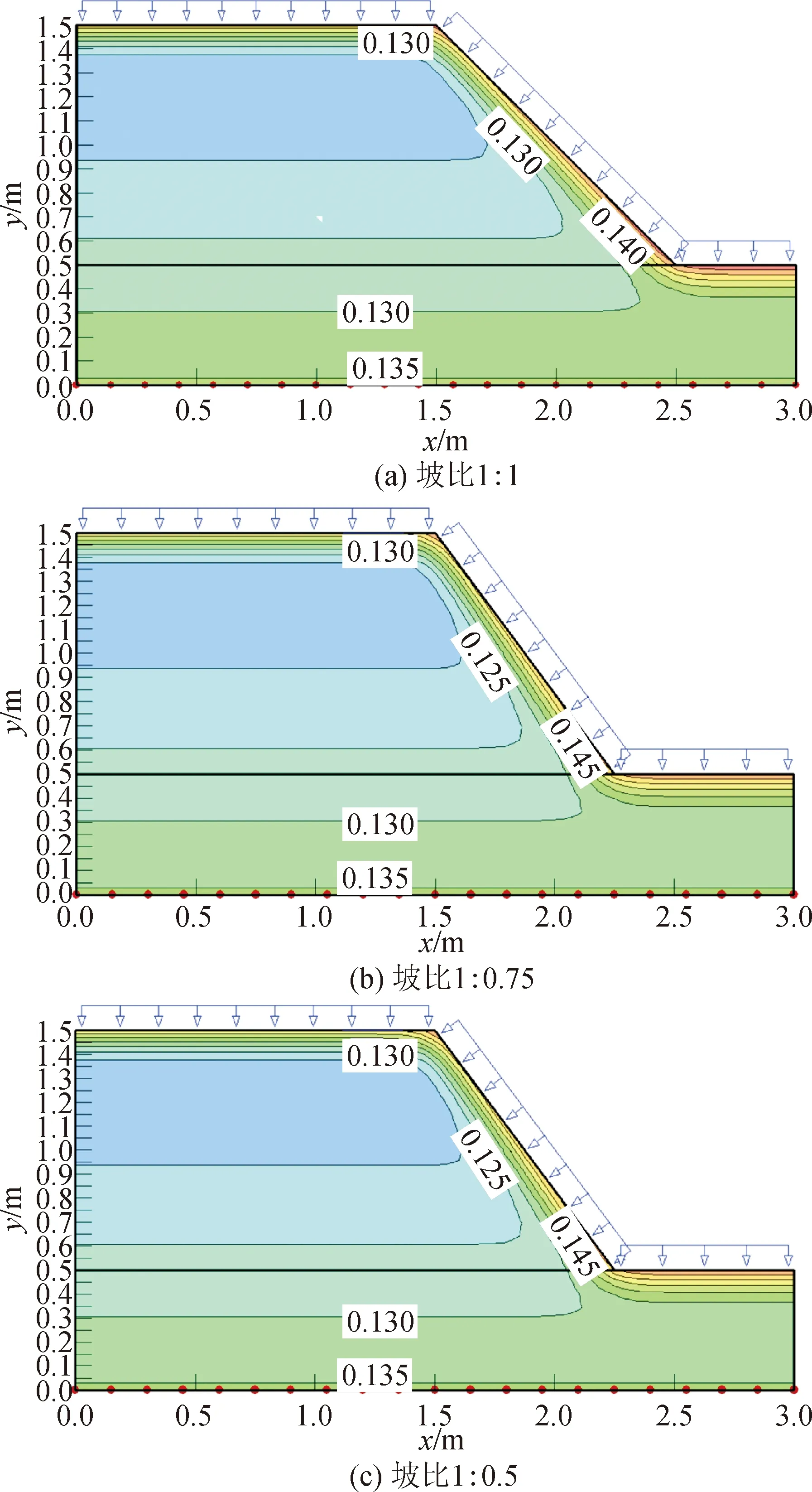
图11 不同坡比含水率分布图Fig.11 Distribution of moisture contents at different slope ratios

图12为数值模拟中不同坡比边坡的坡中测点W10的体积含水率时程曲线，图13为模型试验中测点W10的体积含水率时程曲线。由图可知：降雨开始后，三条曲线均呈现增长趋势，降雨至6～18 h，坡比1∶1的边坡含水率曲线最陡，坡比1∶0.75较陡、坡比1∶0.5最缓，说明坡比越小，坡中降雨入渗速率越大；降雨24 h后，坡比1∶1的曲线峰值最大，坡比1∶0.75次之、坡比1∶0.5最小，含水率分别为26.7%、25.5%和21.1%，以坡比1∶1边坡的坡中含水率为参照条件，坡比1∶0.75、坡比1∶0.5的坡中含水率分别减小1.2%和5.6%，说明坡比越小，坡中土体含水率越高，降雨入渗越充分，入渗深度越大。

图12 数值模拟中测点W10的含水率时程曲线Fig.12 Time-history curves of W10 moisture content in numerical simulation

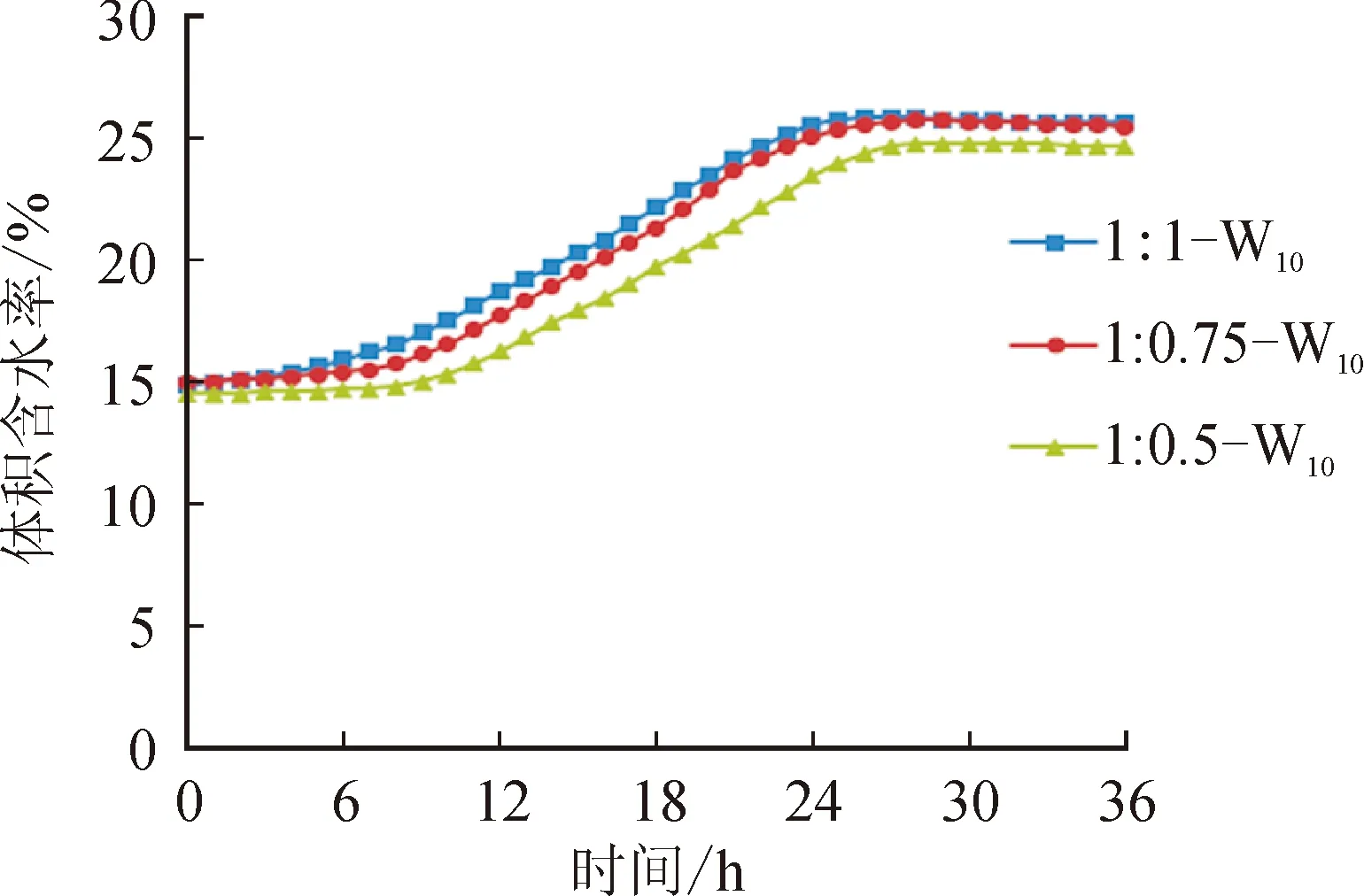
图13 模型试验中测点W10的含水率时程曲线Fig.13 Time-history curves of W10 moisturecontent in the model test

4 结 论

1) 在降雨过程中，同一边坡的坡顶降雨入渗速率最快、坡脚较快，坡中最慢，且降雨入渗深度呈现出坡脚入渗最深、坡顶较深、坡中最浅的特点，随着入渗深度的增加，雨水入渗能力减弱；对于不同坡比的边坡，当降雨持续6～12 h，随着坡比的增大，坡中处体积含水率、基质吸力的变化速率和峰值均减小，坡脚处含水率、基质吸力的变化速率和峰值均增大，表明坡比越大，坡中入渗速率越慢，坡脚入渗速率越快。

2) 不同坡比边坡的湿润锋深度差异较大，坡比1∶1边坡的坡中湿润锋深度在20～25 cm之间、坡比1∶0.75边坡的坡中湿润锋深度在15～20 cm之间、坡比1∶0.5边坡的坡中湿润锋深度在10～15 cm之间，表明坡比越大，坡中入渗速率越慢，入渗深度越浅。

3) 对于不同坡比的边坡，在降雨入渗过程中，坡比越大，坡面雨水向坡脚流动的趋势越强，坡面降雨侵蚀作用越显著，径流现象越明显，冲刷破坏越严重，降雨结束后，坡肩处冲蚀沟发育越好，坡脚处堆积的淤泥层越厚。