不等粒径非饱和土湿吸力量化计算及影响因素分析

邓钟尉

(1.广州市城市规划勘测设计研究院，广东 广州 510060； 2.广东省地质过程与矿产资源探查重点实验室，广东 广州 510275)

1 引 言

非饱和土是一种由气相、液相、固相以及水气交界面构成的四相土[1]。基于粒间吸力[2](包含湿吸力)的非饱和土有效应力原理概念清晰，物理意义明确，初步阐明了A.W.Bishop单应力状态变量[3，4]中参数χ和D.G.Fredlund双应力状态变量[5，6]中tanФb的物理意义，基于粒间吸力(包括湿吸力)的非饱和土抗剪强度理论，一方面统一了前人的研究成果，另一方面避免了在研究非饱和土强度理论中存在的误区，逐渐为国内外的众多学者所接受。

吸力[7]问题的研究是非饱和土土力学研究的理论基础，学者们很早以前就已经认识到，由土颗粒的微观接触模型着手研究非饱和土的吸力具有重要的理论意义和实用价值。G.Lian和C.Thornton[8]推导出了等粒径球形颗粒间毛细吸力和粒间附加应力的近似计算公式。K.Shimada，H.Fujii(2000)[9]基于等粒径球形土颗粒接触模型，推导出附加有效应力与饱和角的关系，并进一步探讨了颗粒半径和颗粒堆积方式对土体有效应力及强度的影响。贾其军(2004)[10]基于Fish公式，推导出了等粒径球形土颗粒间由基质吸力和表面张力引起的附加有效应力的解析解。

汤连生[2，11]等在提出湿吸力概念的基础上，经过理论推导，初步给出了微观湿吸力与饱和角、接触角等微观状态量间的计算表达式，并给出了规则堆积情况下，宏观湿吸力Sa和微观状态量间关系式。张鹏程[12]基于等粒径球形土颗粒模型，推导出了湿吸力与含水量、孔隙比及干密度间的定量计算公式。

以往非饱和土吸力的研究大多是建立在等粒径球形颗粒接触模型的基础上，本文假设土颗粒间的接触模型为不等粒径球形颗粒，从理论上推导出的微观湿吸力与饱和角、接触角、颗粒半径间的关系式，并编写了程序，对计算表达式进行了计算。

2 微观湿吸力公式推导

2.1 微观湿吸力量化公式推导

实际土体中土颗粒大小不一，大颗粒形成的孔隙往往被小颗粒填充，相邻土颗粒的半径往往不同，本文建立不等粒径球形土颗粒计算模型，推导非饱和土湿吸力和饱和角、接触角、颗粒半径间等微观状态指标之间的计算表达式。

(1)模型假设

土颗粒间不等粒径球形颗粒接触模型，如图1所示，模型假设如下：

图1 土颗粒接触模型示意图

①土颗粒间的接触为不等粒径球形颗粒；

②土颗粒间收缩膜的形状为球形曲面；

③不考虑重力对收缩膜的影响。

(2)基质吸力与表面张力的关系

根据热力学[13]中的基本原理，假设颗粒间的弯液面形状为球形曲面，相邻土颗粒的半径为R1和R2，固(土颗粒)—液(孔隙水)接触角为θ，土颗粒间与某一含水量对应的饱和角分别为Φ1和Φ2。基质吸力pc为孔隙气压力ua和孔隙水压力uw之间的差值，根据Young-Laplace公式，基质吸力pc的计算公式为：

(1)

式中，Ts为表面张力系数[13]，对于温度和水化学性质特定的液体可视为定值，水温为20°C的纯水，可取Ts=72.7×10-3N/m；r1为弯液面的曲率半径；r2为弯液面到球心连线O1O2的最短距离，则r1和r2的表达式为：

(2)

(3)

联合式(1)～式(3)即可得到不等粒径球形颗粒间微观基质吸力pc与颗粒半径R1和R2、饱和角Φ1和Φ2以及固-液接触角θ间的计算表达式。

(3)微观湿吸力与和表面张力的关系

由土颗粒接触模型可知，孔隙水在土颗粒表面的搭接为一圆周，基质吸力的作用面积为球冠的面积，基于弯液面形状为球形曲面假设，在微观状态下，土颗粒间表面张力Ts与基质吸力pc之间存在以下平衡关系：

(4)

即：

(2πR1sinφ1*R1(1-cosφ1)+2πR2sinφ2*R2(1-cosφ2))pc=(2πR1sinφ1*Tscos(θ+φ1)+2πR2sinφ2*cos(θ+φ2))Ts

(5)

整理得：

(6)

由上述方法即式(6)得到的理论基质吸力与目前广泛采用的即(1)式得到的基质吸力在概念上是一致的，其数值大小均等于孔隙气压力与孔隙水压力之间的差值。基质吸力在微观上是表面张力的竖直分量，在宏观上表征的是土体吸水的能力，即基质势。

土颗粒间由弯液膜表面张力产生的拉力，即以牛顿为单位的微观湿吸力为Fps：

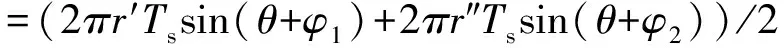
(7)

整理得：

Fps=(πR1sinφ1sin(θ+φ1)+πR2sinφ2sin(θ+φ2))Ts

(8)

根据文献[11]，把以牛顿为单位的微观湿吸力Fps在面积(πr′2+πr″2)/2上求平均，即可得到微观湿吸力ps：

(9)

把r′、r″代入上式得：

(10)

上式即为微观湿吸力与表面张力的关系，同时，微观湿吸力的大小受颗粒半径R1和R2、饱和角Φ1和Φ2、接触角θ的影响。

根据作用在两不等粒径土颗粒上的微观湿吸力ps是一对平衡力，其大小相等，即：

Tssin(θ+φ1)*2πR1sinφ1=Tssin(θ+φ2)*2πR2sinφ2

(11)

整理得：

(12)

由上式可知，饱和角Φ1和Φ2与两颗粒半径R1和R2存在函数关系。

3 微观湿吸力量化计算

微观湿吸力是表面张力垂直于土颗粒接触面的分量，是饱和角、颗粒半径及接触角的函数，本文通过编制程序进行计算，分析不同接触角下饱和角与颗粒半径的量化关系，探讨微观湿吸力与上述影响因素之间的关系。

3.1 不同接触角下饱和角与颗粒半径的量化关系

公式(12)表明，微观状态量接触角θ、饱和角Φ1和Φ2与半径比R1/R2之间存在密切的关系，公式(12)可编制程序进行迭代计算，接触角分别取0°、5°、10°和15°时，不同半径比的条件下，饱和角Φ1和Φ2之间的关系，计算结果如表1所示，曲线如图2所示。

由图2可知，对应于同一接触角θ，大颗粒对应的饱和角Φ1要小于小颗粒对应的饱和角Φ2，随着颗粒半径比的增大，饱和角关系曲线逐渐变得陡峭，说明相邻颗粒半径差异越大，对应的饱和角差异越大。此外，同一接触角对应的饱和角均存在临界值，此时土体的饱和度接近100%，事实上，当接触角和饱和角达到临界值时，弯液面的基质吸力已经趋近于零，此时，小颗粒已被水环包围，形态也会发生改变。

图2 不同接触角下Φ1和Φ2关系曲线

随接触角θ增大，饱和角关系曲线的后半段上升趋势逐渐明显，这意味着随着大颗粒饱和角的减小，小颗粒的饱和角需要增大才能保持弯液面的几何形状。，理论分析结果与文献[14]的实验分析结果相吻合。

接触角θ、饱和角Φ1和Φ2与半径比定量关系表 表1

3.2 微观湿吸力影响因数分析

由微观湿吸力和表面张力的关系式，即式(10)可知，微观湿吸力与表面张力存在函数关系，同时受颗粒半径R1和R2、饱和角Φ1和Φ2、接触角θ的影响。表面张力系数Ts受温度、水化学性质的影响，对于温度为20°C的纯水可取72.7×10-3N/m。

此处仅考虑接触角θ=5°的情况，以颗粒半径比R1/R2=2为例，探讨基质吸力、微观湿吸力与颗粒粒径大小、饱和角的关系，计算结果如表2所示，曲线如图3、图4所示。

接触角θ=5°时基质吸力、微观湿吸力与颗粒半径、饱和角定量关系 表2

由基质吸力、微观湿吸力与颗粒半径、饱和角定量关系计算结果及图3和图4可知，当粒径比相等时，微观湿吸力和基质吸力都与颗粒半径大小成反比，颗粒半径越大，微观湿吸力和基质吸力越小，颗粒半径越小，微观湿吸力和基质吸力越大。随着饱和角Φ1的增大，微观湿吸力和基质吸力单调减少，在饱和角较小时，曲线的斜率较大，二者减小的趋势更明显，基质吸力减小的速度要快于微观湿吸力。当饱和角趋近某一特定值时，微观湿吸力和基质吸力都趋向于零，对应颗粒半径R1=1 mm、R2=0.5mm的情况，微观湿吸力和基质吸力减小到0，此时的饱和角为Φ1=24.39°，Φ2=41.53°，即为该状态下土体的最大饱和角。随着土颗粒半径的减小，土体的最大饱和角有增大的趋势。

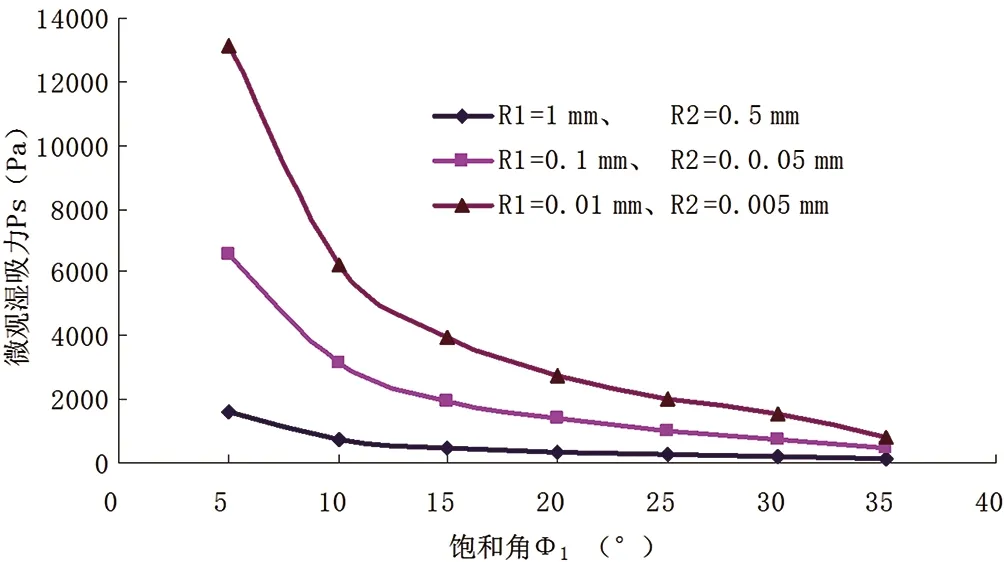
图3 粒径比相等、粒径不等情况下微观湿吸力与饱和角Φ1的关系

图4 粒径比相等、粒径不等情况下基质吸力与饱和角Φ1的关系

4 结 论

本文建立了不等粒径球形土颗粒接触模型，通过土颗粒周围气-液界面毛细现象、表面张力等的研究，推导出微观湿吸力表达式，并对微观湿吸力进行了量化计算，得出了以下结论：

(1)当粒径比相等时，微观湿吸力和基质吸力都与颗粒半径大小成反比。

(2)微观湿吸力和基质吸力都随饱和角的增大而减小。

(3)存在最大饱和角，当饱和角趋近最大饱和角时，微观湿吸力和基质吸力都趋向于零。

本文的基于不等粒径球形颗粒模型，从理论上推导出非饱和土微观湿吸力的计算表达式，对不等粒径非饱和土的宏观湿吸力、任意堆积甚至颗粒形状不规则的实际土体，有待进一步研究。