确证逻辑：一种基于证据的认知逻辑

朱建平

（苏州大学政治与公共管理学院哲学系，江苏 苏州 215123）

确证逻辑：一种基于证据的认知逻辑

朱建平

（苏州大学政治与公共管理学院哲学系，江苏 苏州 215123）

在当代知识论中，柏拉图“确证的真信念”（justified true belief）的知识的三元定义仍是知识论的核心定义。在形式语义学中，这个定义中的“真信念”成分通过模态逻辑和可能世界语义学，已经给出了一种形式的刻画。但与此同时，柏拉图定义中的“确证”要素长期以来却缺乏一种形式的表征。于是，将“确证”引入形式认识论之中而构建的逻辑系统成为一种新型的认知逻辑。具有确证的认知逻辑连同通常的知识算子□F（F是可知的）包含了对确证的形式处理（断定t:F意味着t是对F的确证）。同时，该系统还为这种逻辑提供了可能世界语义学，该语义学扩展了具有确证断定的t:F的菲廷类型的克里普克模型。

确证；确证逻辑；认知

一、确证与认知逻辑

历史上，逻辑的研究一直集中于认识论和本体论两个方面。从亚里士多德直到19世纪，逻辑关注的焦点主要是认识论。逻辑处理论证、演绎和证明。它提供区别正确论证与不正确论证的标准，并使用推理来扩展我们的知识。自布尔和弗雷格以来，逻辑转向本体论的方向。逻辑开始关心设计一种能充分表征世界和内容的语言。

尽管逻辑学家也关心认知领域，在当代逻辑理论中却很难接纳认知问题。演绎系统往往不太适合于探讨真实的论证；它们的任务偏重于编纂逻辑语义学上可区别的句子或者陈述，或者由前提和结论的组合而构造的抽象推理。在这种情况下，主要是与本体论有关的语义学在逻辑中占据主导的地位。但自上世纪中期，逻辑的研究开始向认知领域渗透，这种渗透的标志之一就是确证认知逻辑的出现①。

确证理论是认识论理论的一部分，它试图理解命题和信念的确证问题。认识论者关心各种不同的信念的认知特征，这些特征包括确证、保证、合理性和可能性。大致地说，确证是人们持有某信念的理由。确证理论主要关注命题或者陈述的确证。

作为确证理论的一部分，确证认知逻辑主要与当代知识论中的知识定义相关。在当代知识论中，柏拉图作为确证的真信念的知识的三元定义仍是知识论的核心定义。其中的知识三要素（确证、真、信念）一般被认为是拥有知识的必要条件。而其中的“真信念”经过辛迪卡（Hintikka）的技术处理，已经在相当程度上通过模态逻辑和可能世界语义学的方式，给出了一种其原子模态是“F是已知的”和“F是被相信的”形式表达。而关于确证条件的问题却始终缺乏一种形式的表征。范本瑟姆（J.van Benthem）在他的认知逻辑的论文中首次讨论了带有确证的形式认知逻辑系统[1]。这样一种逻辑包含□F（F是可知的）以及t:F（t是F的确证）的形式断定。

确证的认知逻辑（以下简称确证逻辑）通过将辛迪卡类型的认知模态逻辑与出现于证明逻辑中的确证演算相结合的方式，把确证引入于形式认识论[2]。特别是，确证试图将认知模态逻辑S4和证明逻辑（Logic of Proofs）LP相组合。这种处理的好处是，无论是作为知识或（和）信念的□F，还是作为确证要素的t:F，它们能够被相互独立地加以选择，从而在表达上显示出较强的灵活性。

建立在证明逻辑LP基础上的确证的认知系统使用了下列假定：（1）每一公理有一确证；（2）确证是可检查的；（3）陈述的确证断定蕴涵关于这陈述的知识；（4）任何确证与其他确证之间的关系是协调融贯的。当然，也存在着其他一些确证系统，其中的每一个系统都捕捉到了相关确证性质的集合。这就为各种带有确证的认知逻辑系统的发展开辟了道路。

确证概念的形式化极大地扩展了认知逻辑的表达力，它为认识论及其应用的形式研究提供了新工具。以下是一些受到这些新的发展影响的认识论概念：

第一，长期以来，由于认知逻辑和主流认识论之间的鸿沟造成的确证逻辑的缺乏，直接影响到布劳维尔—海丁的直觉主义逻辑语义学形式化和哥德尔可证逻辑的语义学发展。确证逻辑的出现增加了一个期许已久的数学的确证概念，使得逻辑本身更富表达力。有了确证逻辑人们就具备了关于确证推理的能力，就能够比较关于相同事实的不同证据，能够测量证据的复杂性，因而可以将知识的逻辑与一个丰富的复杂性理论联系起来。

第二，确证逻辑为与柏拉图作为确证的真信念的知识定义相一致的知识算子提供了一种新颖的语义学，进而可用于对柏拉图知识定义以及葛提尔对该定义所提供的反例的语义学分析[3]。

第三，确证逻辑为知识逻辑提供了基于证据的基础，按照知识的逻辑，F是可知的被解释为：F有一个充分的确证。在此基础上，确证逻辑提供了一个新颖的追踪事实的机制，该机制对从更大的证成实体提取强有力的证据提供了极有价值的工具。

第四，传统的辛迪卡形式对知识的模态逻辑处理有逻辑大全（logical omniscience）的缺陷。这是由不切实际地规定认知体知道假定的所有的逻辑后承而引起的[4]。通常的认知模态□F应被看作是“潜在的知识”或者“可知性”，而不是实际的知识。带有确证的认知模态系统以一种自然的方式处理了逻辑大全问题。如果没有对F的清晰确证t的表达，一确证的知识t:F就不能被断定，因而被确证的知识不再是逻辑大全的。

第五，具有确证的认知逻辑对常识知识提供了一种新处理[5]。它证明确证的知识是常识知识的一种特定的建设性的形式，并且其本身也能用于解决特定的问题。与传统的普通知识相比，确证的知识显得更加灵活，在某些方面也更容易理解和掌握。

有众多的例子可以在确证的认知模态逻辑中以更为自然的方式加以处理。例如，关于知识的内涵和外延的表达。与辛迪卡的知识逻辑相同，知识陈述“F是已知的”（□F）依然是外延的。反之，新的确证陈述t:F已经是内涵的了。的确，由t:F成立，且G与F等值，并不能由此产生t:G。如果存在着一个对F→G的证成s，那么对G的一个证成是s和t的某些函项，这函项一般地说不同于t。带有确证的认知逻辑的形式公理和规则捕捉到了这一区别。

总之，知识、信念和证据是其意义跨越许多人类活动领域的重要概念。这些领域包括人工智能、计算机科学、数学、经济学、博弈论、密码学、哲学和其他学科。确证逻辑对这些学科的发展产生了富有冲击力的影响。本文描述确证逻辑理论的基本要素和语义学解释。作为一个整体，确证逻辑目前仍处在发展之中，这里所讨论的问题只是它在该时期的一个横断面的素描而已。

二、确证逻辑的基本要素

以下是最基本的确证逻辑的句法和公理系统。

（一）确证逻辑的语言

为了建构确证逻辑的形式说明，人们必须作出某些基本的结构性假定：确证是具有某种结构和运算的抽象对象。一个好的确证事例由形式证明所提供，而形式证明长期以来一直是数理逻辑和计算机科学研究的对象。

确证逻辑是一合并了认知断定t:F的形式逻辑的框架，其中t:F代表‘t是对F的确证’。确证逻辑并不直接分析超越公式t:F之外的t确证F意味着什么，而是试图公理化地刻画这种关系。这类似于布尔逻辑处理它的连接词，比如说对析取的处理并不是去分析公式p∨q，而是宁可假定某些逻辑公理，以及关于这些公式的真值表。

确证逻辑从最简单的基础—经典布尔逻辑开始，由罗素（Russell）、古德曼-克里普克（Goldman-K ripke）、葛梯尔（Gettier）和其他人所提供的范例，能够通过使用布尔确证逻辑被处理。认知逻辑的核心由建立在经典布尔逻辑基础上的模态系统 （K,T,K4,S4,K45,KD45,S4等）构成，它们中的每一个都提供了伴随有基于布尔逻辑的相应的确证逻辑。最终，确证的行动并不总是被假定的。这使得它有可能在涉及信念而非知识问题的认识论时，捕捉到所讨论问题的本质。

确证逻辑的基本运算是 ‘贴合’（app lication）和‘加’（sum）。贴合运算是一个以确证s和t为论元，以确证 s:t为值，使得如果 s：（F→G）和 t:F，那么[s·t]:G的一个函项。用符号表示即为

这就是在组合逻辑和兰姆达演算 （λ-calculi）中所假定的确证的基本性质，也是在布劳维尔-海丁-柯尔莫格洛夫（Brouwer-Heyting-Kolmogorov）语义学，克林（K leene）现实性理论以及证明逻辑LP所假定的确证的基本性质。

任何两个确证都能够安全地与某些更为宽泛领域中的论题相组合。这可以通过使用加运算‘+’来实现。如果s:F，那么不管证据t可能是什么，被组合的证据s+t依然是F的确证。更恰当地说，运算‘+’是一个以确证s和t为论元，以s+t为值——该值是被s或者被t所确证的每一事物的函项。

作为一个理由，人们可以想象s和t作为百科全书的两卷，s+t作为这两卷的集合。想象其中的一卷，比如说s，包含了命题F的充分的确证，即s:F。进而更大的集合s+t也包含了对F的充分确证，[s+t]:F。

（二）基本确证逻辑J0

确证词汇由确证变元x,y,z,…和确证常项a,b,c,…，通过运算‘?’和‘+’的方式建构而成。以下考虑的更加精致的逻辑也允许关于附加的运算。常项指称系统中的那些并不被分析的原子确证；变元指称未指定的确证。确证的基本逻辑J0按下列方式被公理化。

经典逻辑

经典命题公理和肯定前件的推理规则

应用公理

加法公理

（三）逻辑意识和常规范

逻辑意识原理说的是逻辑公理是当然被确证的：一认知体将逻辑公理作为被确证的而加以接受。如同以上所表明的，在某些认知情况下，逻辑意识可能是太强了。然而，确证逻辑提供了表达不同逻辑意识色调的常规范的灵活机制。

当然，人们在假设和假设的确证之间做出区别。在确证逻辑中的常项被用于代表在对它们不再做进一步分析的情况下的一个假定的确证。假设人们希望规定一公理A对知道者而言是被确证的。对某些（具有索引1的）证据常项e1，人们简单地规定e1:A。更进一步地说，如果人们希望规定这个新的原理e1:A也是被确证的，对某些（具有索引2的）常项e2，人们能够规定e2:(e1:A)等等。保持对索引的这种追踪并没有必要，但在判定程序中它是容易的和有帮助的。这类对一给定的逻辑的所有的假定的集合称之为常规定。以下是它的形式定义：

对一给定的确证逻辑的常规定CS是一形式为公式

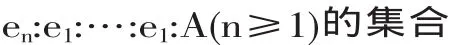
其中 A 是 L 的公理，e1,e2，…，en是指数为 1，2，…，n的类似的常项。人们假定CS包含了所有的中间的规定，即当en:en-1:…:A在CS中，那么en-1:…:en-1:…e1:A也在CS中。

在文献中已经对常规定施加了若干特定的条件。下列是最一般的条件。

空：

CS=Φ。这对应于一绝对的怀疑认知体，它相当于与逻辑J0共事。有限：

CS是公式的有限集合。这是一个充分有代表性情况，因为在确证逻辑中的任何特定的推演将仅涉及常项的有限集。

公理上恰当：

每一公理，包括那些通过常规定本身而新获得的公理都有一确证。在形式的情况下，对每一公理A存在着一恒常的e1，使得e1:A在CS中，且如果en:en-1:…:e1:A∈CS，那么 en+1:en:en-1:…:e1:A ∈ CS。 公理化的适当常规定对于确保内在化性质是必要的。总计：

对每一公理A和任意常项e1,e2,…,en，

名称TCS留作总计的常规定。自然地，总计常规定是公理上适当的。

我们现在可以指定具有常规定的确证逻辑。

令CS是一常规定。Jcs是逻辑J0+CS；公理是由J0加CS的元素组成的，唯一的推理规则是肯定前件式。

确证逻辑：

J是逻辑J0+公理内在化规则。新的规则说：

对每一公理A和常项e1,e2推出en:en-1:…:e1:A。

后者具体体现了对J的不加限制的逻辑意识的思想。一个类似的规则出现在证明逻辑LP中，古德曼已经预见到这一点。如同在公理的适当常规定中所表达的，逻辑意识是模态逻辑中必然化规则的具体体现，但它仅限于公理。

确证逻辑系统的关键特征是它有能力内在化作为可证的确证断定的它们自己的推演。这一性质被哥德尔在1938年所预言。

定理1：对每一公理上适当的常规定CS，JCS享有内在化：

对某些确证词汇p而言，如果├F，那么├pF。证明：关于推演长度的归纳。假定├F。如果F是J0的元素，或者是CS的元素，那么存在着一个常项en(其中的n可能是1)，使得e:F在CS中，因为CS是自明上恰当的，那么en:F是可推演的。如果F通过肯定前件的规则从X→F和X获得，那么依据归纳假设,对某些s,t├s:(X→F)和├t:X。使用应用公理├[s.t]:F。

（三）事实性

事实性（factivity）说的是确证对认知体得出结论的真而言是充分的。以下是事实性的具体体现：

事实性公理t:F→F。

事实性公理与认知逻辑中的真公理□F→F有相似的动机，而后者作为知识的基本性质被广泛承认。

与贴合原理和加原理不同，确证的事实性在基本的确证逻辑系统中并不是必须的，这使得它们有能力表达局部的和事实性确证。事实性公理作为一个数学证明的主要特征出现于证明逻辑LP之中。的确，在这一情景之中事实性显然是有它的价值的：如果存在着一个关于F的t的数学证明，那么F必定是真的。

事实性公理作为导向知识的确证而被接受。但如同葛梯尔的例子所表明的那样，事实性本身并不担保知识。

事实性确证的逻辑

·JT0=J0+事实性

·JT=J+事实性

对应于常规定CS的系统JTcs按照2.3中的方式被定义。

（四）正内省

知识的通常原理之一是识别“知道”和“知道人们知道”。在模态的情况下，它对应于□F→□□F。这一原理有一个充分清晰的对应物：一认知体接受t作为F的充分证据的事实起着一种作为t:F的充分证据的作用。通常这些“元证据”有一种物理学的形式：一指称报告证实在论文中的证明是正确的；一计算机证实给出作为一输入的形式证明t的输出；t是一F的证明的形式证明，等等。为此目的正内省运算“！”被增加到这一语言上来；进而人们假定给定t，认知体形成一关于 t：F 的确证！ t，使之 t：F→!t:(t:F)。在这一运算形式中正内省算子第一次出现在证明逻辑LP之中。

正内省公理：t：F→!t:(t:F)。进而我们定义：

·J4:=正内省；

·LP:=JT+正内省。

逻辑 J40，J4，J4cs，LP0和 LPcs以自然的方式被定义。定理1对J4cs和LPcs的直接类比也同样成立。

在正内省公理的前面，人们能够将公理内在化规则的范围限制在其形式并非是e:A的内在化公理范围之内。这就是它在LP中做事的方式：因而公理内在化能够通过使用!!e:(!e:(e:A)，来代替e3:(e2:(e1:A))的方式而被模仿。常规定的概念也因而被简化。这样一种修正是次要的，它们并不影响确证逻辑的主要定理和应用。

（五）负内省

帕库特（Pacuit）和卢布佐娃（Rubtsova）将负内省运算“?”看作是对一给定的确证断定是假的证实[6][7]。对这一运算有所考虑的动机是正内省运算“!”可能被视为提供了关于确证断定t:F的决定性证实的能力，所以，当t并不是对F的确证时，这一“!”将推断出┐t:F。通常这是计算机证明证实以及在形式理论中证明检查器的情况。然而，这一动机是有细微差别的。证明证实和证明检查器的例子都涉及t和F作为输入，反之，帕库特-卢布佐娃的形式?t表明只有输入“?”是确证t。最终?t被认为证实了命题┐t:F。这一运算“?”对形式的数学证明并不存在，因为?t应当是无穷多的命题┐t:F的一单一的证明，这是不可能的。

负内省公理┐t:F→?t:(┐t:F)。

系统被定义为：

这些定义可以很自然地扩展到J45cs，JD45cs和JT45cs之中。 定理 1 对 J45cs，JD45cs和 JT45cs的直接类比也成立。

三、语义学

目前，在文献中的确证逻辑的标准语义学起源于菲廷（M.C.Fitting），他所使用的模型一般称之为菲廷模型[8]。可能世界确证模型是我们熟悉的知识和信念的逻辑的可能世界语义学，与由Mkrtychev引入的对确证词汇的机械说明相结合的产物。限于篇幅本文只介绍单认知体可能世界确证J模型

为精确起见，本文给出Jcs的语义学（中的CS是任意常规定）的定义。形式上，Jcs的可能世界确证逻辑的模型是一结构 M=〈G,R,E,V〉。 其中，〈G,R〉是一标准K框架，G是可能世界的集合，R是关于可能世界的二元关系，V是从命题变元到G的子集的映射，它指派原子命题在可能世界的真值。

新的词项是E，一个将确证词项和公式映射为世界的集合的函项。其直觉思想是，如果可能世界г在E（t,X）中，那么t是关于在世界г中的X的相关或者可靠证据。人们不要把相关证据看作是决定性的，宁可说，最好将其看作是能够在法庭上被认可的证据：这一证据，这一文件是陪审团将要检查的一些东西，是相关的事物，但它的真值状态尚未被考虑。证据函项必须满足某些条件。

给定Jcs的可能世界确证模型M=〈G,R,E,V〉，在可能世界г中公式X的真值由M,г├X所指称的公式X的真值被要求满足下列标准条件：

对每一г∈G:

1.M,г├P当且仅当 г∈V(P)(P为命题字母)；

2.并非 M,г├⊥；

3.M,г├X→Y当且仅当并非M,г├ X或者 M,гY。

这些只是说原子事实是任意指定的，命题连接词在每一可能世界中起真值函项的作用。关键词项如下：

1.M,г├(t:X)当且仅当 г∈E(t，X),且对每一个具有гRΔ的Δ∈G，我们有M,Δ├ X。

这一条件分为两部分。从句要求对每一个使得гRΔ的 Δ∈G，M,Δ├ X是我们熟悉的在г中 X被相信或者可信的辛迪卡-克里普克条件。进而，非形式地说，t:X在一可能世界是真的，如果在通常认知逻辑的意义上在那个世界里是可相信的，且t是指那个世界中的D的相关证据。

重要的是要意识到，在这一语义学中，人们基于这一世界里的特定理由——或者因为它是不可信的，或者只是因为理由不恰当——而不相信某些事物。

对证据函项仍然施加了某些条件，而且假如人们给出s和t作为确证，那么常规定也必须考虑在内。人们能够以两种不同的方式对它们加以组合：同时使用来自二者的信息，或者仅使用它们其中一个的信息，通过公理的方式引入“?”和“+”的符号从而产生出关于确证词项的基本运算。

假定s是关于一蕴涵式的相关证据，且t是前件的相关证据，那么s和t一起提供了后件的相关证据。以下关于证据函项的条件被假定：

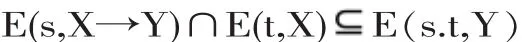
附加上这一条件，

s:(X→Y)→(t:X→[s.t]:Y)的有效性是被保证的。如果s和t是证据词项，人们可以说某事物被s或者t所确证，而不必考虑究竟是它们中的哪一个。下列要求也被施加于证据函项：

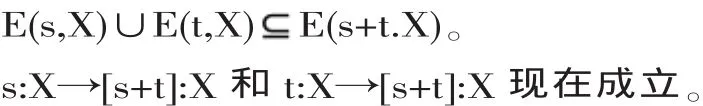
最后，常规定CS也在考虑范围之内。让我们回想起常项是用来表示被即刻接受的基本假定的理由。模型M=〈G,R,E,V〉满足恒常说明CS，只要：如果c:X∈CS，那么 E(c,X)=G。

四、结语：方兴未艾的确证逻辑

作为一个新兴的认知逻辑的分支，最初的确证逻辑系统—证明的逻辑LP是由阿特姆夫在1995年引入的。在这一系统中体现系统基本性质的内在性、实现性、算术的完全性被第一次确立。LP为哥德尔的可证性逻辑S4提供了一种所期望的语义学，进而又为作为直觉主义命题逻辑的布劳维尔-海丁-柯尔莫格洛夫语义学提供了形式的处理。LP的认知语义学和完全性在2005年由菲廷首次确立，而Mkrtychev确立了LP的符号模型和可判定性。紧接着布里兹涅夫和库兹涅茨作出了可判定性和复杂性结果的综合评述。建立在确证知识基础之上的常识知识的更为一般的处理由阿特姆夫作出。伦尼研究了确证逻辑的博弈语义学和具有确证的动态认知处理。确证逻辑和逻辑大全之间的联系最终由阿特姆夫给出。这种处理对克里普克、罗素和葛梯尔的例子给出了形式分析并被用于悖论、证成和隐藏假定分析和消除余冗的解决。在迪恩和黑川的著作中确证逻辑被用于分析知识者和知识性悖论的解决。

注：

①在当代文献中，英文“justification”也可译为“证成”。本文仍循传统，取“确证”之意。但两个概念均可在本文的语境中使用。

[1]J.van Benthem.Reflections on epistem ic logic[J].Logique&Analyse,1991,（133）：5-14.

[2]S.Artemov.Logic of Proofs.Annals of Pure and App lied Logic[J].1994,（67）：29-59.

[3]L.Bonjour.The Coherence Theory of Empirical Know ledge[M].Philosophical Studies,v.30,pp.281–312.Reprinted in Contemporary Readings in Epistemology,M.F.Goodman and R.A.Snyder(eds).Prentice Hall,1993.70–89.

[4]R.Fagin,J.Halpern,Y.Moses,M.Vardi.Reasoning About Know ledge[M].M IT Press,1995.

[5]S.Artemov.Evidence-based common knowledge[M].Technical Report TR-2004018,CUNY Ph.D.Program in Computer Science,revised version,2005.

[6]Pacuit,E.A Note on Some Explicit Modal Logics[M].Technical Report,2006,PP–2006–29,Institute for Logic,Language and Computation,University of Amsterdam.

[7]Rubtsova,N.On Realization of S5-modality by Evidence Terms[J].Journal of Logic and Computation,2006，16（5）：671-684.

[8]Fitting,M.The logic of proofs,semantically[J].Annals of Pure and App lied Logic,2005,132(1):1–25.

Logic with Justification:a Proof-based Epistemic Logic

ZHU Jian-ping
(Departmentof Philosophy,School of Politics and Public Administration,Suzhou University,Suzhou,Jiangsu 215123)

The true belief components of Plato’s tripartite definition of knowledge as justified true belief are represented in formal epistemology by modal logic and its possible worlds semantics.At the same time,the justification component of Plato’s definition did not have a formal representation.This paper introduces the notion of justification into formal epistemology.Epistemic logic with justification,along with the usual knowledge operatort:F(Fis known),contains assertionst:F(t is a justification forF).This paper suggests an epistemic semanticswhich augments Kripkemodelswith a natural Fitting-style treatment of justification assertionst:F.

justification；epistemic logic with justification；epistemic logic

B 815.3

A

1000-260X（2014）03-0065-06

2014-01-15

朱建平，哲学博士，苏州大学教授，从事逻辑哲学、逻辑史、内涵逻辑及语言哲学和心灵哲学研究。

【责任编辑：董世峰】