可变形翼型超声速非定常气动力的研究

高彦峰，刘志帆，王晓宏

（中国科学技术大学热科学和能源工程系，安徽 合肥 230026）

可变形翼型超声速非定常气动力的研究

高彦峰，刘志帆，王晓宏

（中国科学技术大学热科学和能源工程系，安徽 合肥 230026）

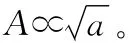
智能飞行器；可变形飞行；超声速流动；气动力；非定常流动

0 引 言

对随着对作战性能和生存能力要求的不断提高，超声速巡航、高速飞行和高机动等特性已成为了人们关注的焦点之一。根据不同的飞行环境和作战任务等要求，飞行器适时调整自身外形布局，使其在整个飞行过程中和执行不同任务时，始终保持飞行全阶段综合性能的最优化，这种具有“智能化”的飞行方式，可以适应巡航、高速飞行和高机动等不同的飞行状态，并具有较好的机动性。智能可变形飞行技术的研究对高机动战斗机及高性能无人机的研制具有重要的应用价值及广泛的发展前景［1-4］。

对于可变外形引起的非定常气动问题的研究，可以追溯到1935年Theodorsen关于机翼振动的经典性工作［5］，20世纪70年代以来，Weis-Fogh、Lighthill、Maxworthy和孙茂［6-9］等人的理论分析和实验表明昆虫飞行中外形改变引起的非定常流动效应是昆虫获得大升力、在空气中实现自由飞行的重要因素，Kramer［10］指出海豚腹部在运动中不断自适应变形是其拥有高速运动能力的主要原因，Wickenheiser［11］等发展了Prandtl的升力线理论，并应用于海鸥式变形翼研究。对于可变形飞行器，Neal等［12］试验研究了低速飞行时变后掠和变展长等对气动性能的影响，Hall等［13］研究了采用变后掠的方式提高微型飞行器的飞行性能，Secanell等［14］研究了爬升、巡航和盘旋等不同飞行状态下的翼型优化问题，陈钱等［15-16］对机翼变形的气动特性进行了实验研究。郭秋亭等［17］通过数值模拟指出跨声速飞行时，机翼折叠与展开过程中其气动特性会发生急剧的变化。

早在20个世纪70年代中期，Morino等［18-19］利用以格林公式为基础的边界元方法计算亚声速和超声速流动问题。刘千刚等［20］将边界元法推广到研究机翼、机身和尾翼组合体的气动力特性，周文伯等［21］利用边界元研究了三维超声速机翼和尾翼组合体在启动过程中机翼对尾翼的洗流影响作用。在过去的研究工作中［22-23］，我们对于可变形儒可夫斯基翼型的二维低速不可压缩和亚声速绕流问题开展了理论和数值研究，将解析解和离散涡方法相结合计算变形翼型的流场及非定常气动力，分析了变形翼型升力系数的准定常计算方法的误差来源，并给出修正方法。机翼变形根据变形方式可以分为分布式小变形，如改变弦长、厚度、弯度等的翼型变形；以及整体式大变形，如后掠角、弯扭和展弦比等。本文将利用以格林公式为基础的边界元方法研究变形机翼进行分布式小变形时的超声速非定常气动性能，即针对可变形翼型二维超声速绕流问题开展初步研究。

1 数学模型

设无穷远处的来流速度为V∞，来流马赫数为Ma∞，来流速度沿x方向，来流和翼型前后缘连线之间夹角为α。为了便于数学上的分析，首先将参照系选择在来流上，从而机翼绕流问题转化为机翼以V∞速度沿-x方向运动的问题，另外我们将坐标系固结在机翼上，采用动坐标系描述机翼运动问题。对于超声速薄翼绕流问题，采用小扰动假设，作为初步研究，本文假设翼型变形速度较小，即忽略了速度势对时间的二阶导数φtt的作用，从而流动速度势φ在整个流场区域满足方程［24］：

物面边界条件为：

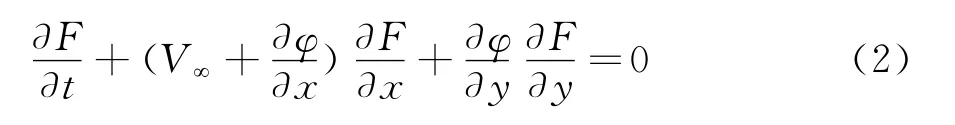
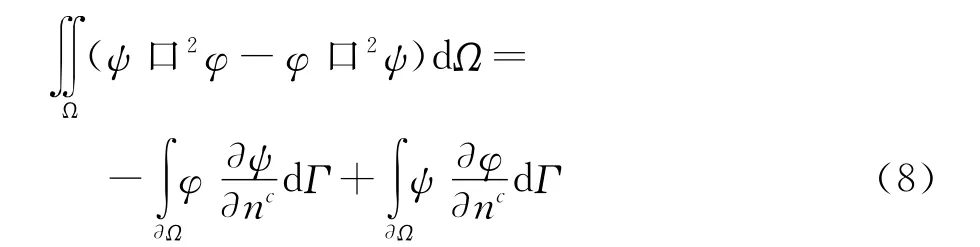
又知算子的口2基本解为［26］：

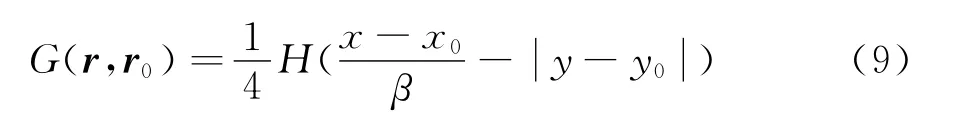
其中，r0和r分别为源点和受扰点，H（·）为Heaviside函数。将基本解代入格林公式即可得到超声速问题扰动速度势的边界积分方程：

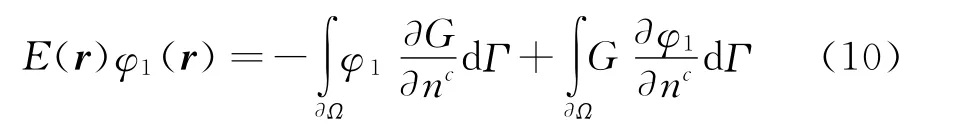
其中当点r在计算区域内时，E（r）＝1；当点r在计算边界上，E（r）＝1／2；当点r在计算区域外时，E（r）＝0。将边界积分方程离散得到：

采用动坐标系下相对运动的伯努利方程计算运动变形翼型的翼面压强：

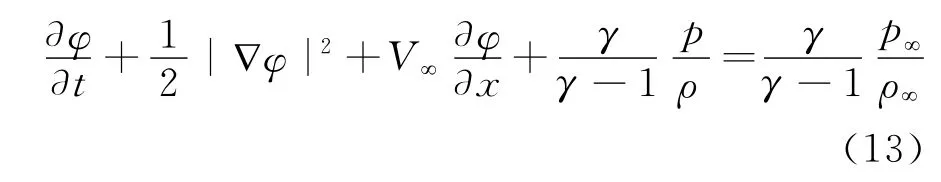
由于薄翼对流场的扰动较小，即｜▽φ｜≪V∞，由方程（13）及理想气体状态方程p＝ρRT可得：

变形翼型的升力系数为：

其中b为半弦长，（Cp）+和（Cp）－分别表示上翼面和下翼面的压力系数，（Cl）准和（Cl）非分别表示超声速可变形翼型的准定常升力系数和非定常附加升力系数：

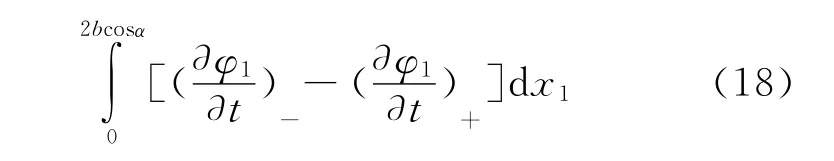
对于可变形翼型，即使选择和机翼一起运动的动坐标系予以描述，在该动坐标系下，翼面位置也会随时间发生变化，这样对翼面上非定常项∂φ／∂t的数值计算需考虑到翼面变形的影响，即t时刻翼面上某点的位置为r（t），在t+Δt时刻该点将运动到r（t+ Δt），为方便起见，我们让翼面上各离散点沿法线方向运动，此时非定常项∂φ／∂t不适合使用两点之间的速度势随时间的变化速率：［φ（t+Δt，r（t））－φ（t，r（t））］／Δt直接予以离散计算，而需考虑该点位置变化带来的影响。由非定常伯努利方程（13）可得：

儒可夫斯基翼型是通过复变函数论中保角变换法得到的一种数学上的理想翼型，由半弦长b、最大弯度f和最大厚度i等三个参数所确定，对于可变形儒可夫斯基翼型，翼型参数是时间i的函数。由于儒可夫斯基翼型在数学上可以用解析形式予以描述，为方便起见，在下节中，我们将以儒可夫斯基翼型为例，研究超声速来流下翼型变形导致的非定常气动力的特性。

2 数值计算及结果分析

选取翼型在初始时刻的状态参数为：弦长为3．8m，最大弯度为0．03m，最大厚度为0．1m，来流与翼型的前后缘连线的夹角为5°；流体比热比为1．41，来流温度为273．15K以及密度为1．29kg／m3。

2.1 变形翼型升力系数与翼型参数之间的关系

在计算中选取马赫数为2．0，我们分别让翼型的半弦长b、最大弯度f和最大厚度τ分别以1．0m／s的速度匀速增加，研究超声速时变形翼型的气动升力系数与翼型参数变化速率之间的关系。图1的计算结果显示，升力系数随着弦长的增加而略为增大，随着最大弯度或最大厚度的增大而减小，在这三个参数中，升力系数对厚度的变化更加敏感。在弦长或弯度的变化过程中，由流场速度势随时间变化率∂φ／∂i导致的非定常附加升力对升力系数无明显贡献，对于升力系数采用准定常方法可以得到较精确的计算结果；而翼型厚度的变化过程中，非定常附加升力对升力系数有着一定的贡献。这和亚声速时变形翼型的非定常气动性能有着明显的不同，在亚声速条件下，在弦长、弯度或厚度的变化过程中，非定常附加升力对升力系数均有着一定的贡献，且弯度变化时非定常附加升力效应更加显著。

忽略翼面变形法向速度的影响，由方程（1）和（3）可得流场速度势φ为半弦长b、最大弯度f和最大厚度t的函数，和翼型几何参数随时间的变化速率无关，即：

于是有：

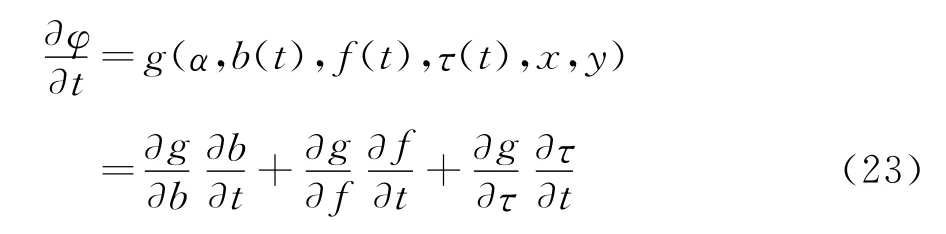
即速度势随时间变化率∂φ／∂t引起的翼面处流场压力变化为翼型几何参数（半弦长b、最大弯度f和最大厚度t）及其随时间变化率的函数，与变形翼型几何参数随时间的二阶及二阶以上的导数无关，从而和不可压缩及亚声速情况相类似［22，23］，由非定常伯努利方程（13）可得，流场速度势随时间变化率引起的非定常附加升力系数仅与当前时刻飞行姿态（来流与翼型前后缘连线夹角）及翼型形状和变形速率有关，与具体的变形历史过程无关，且由方程（23）可得非定常附加升力系数随翼型几何参数变化速率呈线性变化关系（见下小节图2）。变形翼型的升力系数近似等于准定常计算结果叠加上由飞行姿态、翼型形状参数及变形速率所对应的非定常附加升力系数。

图1 三种变形方式下非定常和准定常气动升力系数Fig.1 The unsteady and pseudo-steady lift coefficients for three different kinds of airfoil deformation

2.2 变形翼型升力系数与来流马赫数之间关系

图2 不同来流马赫数时非定常附加升力系数（按马赫数归一化）和翼型最大厚度变化速率的关系Fig.2 Plot of the additional unsteady lift coefficient（normalized according to free-stream Mach number）as the function of the variation rates of the airfoil maximum thickness for different free-stream Mach numbers

2.3 翼型往复变形过程中升力曲线特性分析

若机翼从一种翼型变形到另外一种翼型，然后再变形回到原翼型，对于这往复变形过程，

由于准定常气动升力仅依赖于翼型参数，故采用准定常方法计算气动升力，将得到一条重合的气动升力随翼型参数变化的曲线，但实际变形过程中速度势随时间变化率∂φ／∂t导致的虚拟质量力将诱导非定常附加升力，由于往复变形过程中翼型参数的变化速率不同，甚至可能完全相反，故往复过程中的非定常附加升力将完全不同，从而翼型往复变形过程中升力随翼型参数的变化曲线将是一个闭合回路。由于非定常附加升力系数对厚度变化速率较敏感，本小节主要以厚度变化为例予以讨论。

2.3.1 翼型往复变形过程中升力曲线闭合环与来流速度之间的关系

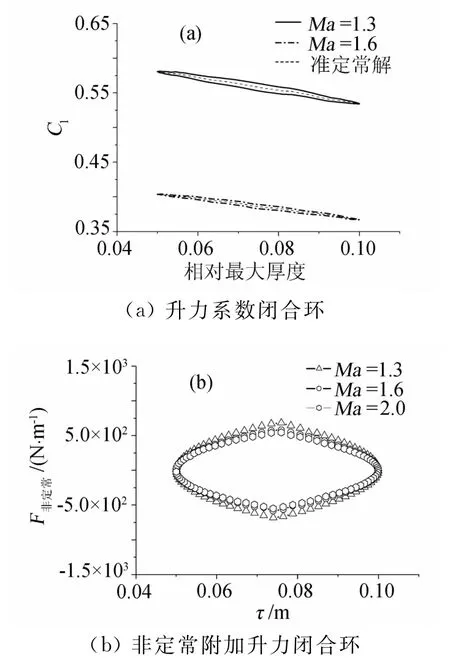
图3 不同马赫数下翼型往复变形时Fig.3 The performance of reciprocating airfoil deformation for different free-stream Mach number

翼型往复变形过程中升力曲线随翼型参数变化的闭合环所围面积，可以解释为往复变形过程中外界所输入的功，所围面积越大则表明需要对外界做的功就越大，在超声速情况下，来流马赫数越高，翼型往复变形所需要做的功就越小，且伴随着来流马赫数的增大，非定常附加升力导致翼型完成往复变形过程所需对外界做的功对来流马赫数趋于不敏感，来流马赫数为1．8与来流马赫数趋于无穷大时的极限值之间相差仅在20%以内，这个特性与亚声速情况有着本质的区别［23］（见图4）。图4的结果还显示在跨声速区域，由线性小扰动模型得到，完成翼型变形需对外界做出的功随来流速度靠近声速而迅速增加并趋于无穷大。尽管在跨声速区域，线性小扰动模型不再适用于机翼流场的计算，此时需考虑非线性作用，但线性小扰动模型在一定程度上反映跨声速区域翼型实现变形难度较大且可能不稳定，从而增加变形控制的难度。

超声速定常流动条件下，升力系数敏感依赖于来流攻角，但我们考察翼型往复变形升力闭合环面积与来流攻角之间的关系，发现不同的来流攻角时该闭合环面积几乎重合，即翼型完成往复变形所需做的功将不依赖于来流攻角（见图5）。

图4 非定常附加升力闭合环面积与来流马赫数之间的关系Fig.4 Plot of the area inside the closed loop for the unsteady additional lift as a function of the free-stream Mach number

图5 不同攻角下非定常附加升力闭合环Fig.5 The closed loops for the unsteady additional lift at various angles of attack

2.3.2 翼型往复变形过程升力曲线闭合环面积与变形加速度之间的关系

图6 非定常附加升力闭合环面积与翼型参数变化加速度之间的关系Fig.6 Plot of the area inside the closed loop for the unsteady lift coefficient as a function of the acceleration rates of geometry parameter variations

3 结 论

本文通过理论分析和数值计算，对可变形翼型在变形速率较小时的超声速非定常气动力特性进行了初步研究。具体结论如下：

（1）超声速条件下，弦长或弯度变化诱导的非定常附加升力很小，而厚度变化诱导的非定常附加升力有着一定的贡献，这些特性与不可压缩或亚声速时差别较大。后者的非定常附加升力对弯度变化的依赖性较大，而对弦长或厚度的变化则较不敏感。

（2）和不可压缩或亚声速时相类似，超声速条件下变形翼型的升力系数近似等于准定常计算结果叠加上由飞行姿态、翼型形状参数及变形速率所对应的非定常附加升力系数，与具体的变形历史过程无关。

（3）着重分析了翼型往复变形时的气动特性，在超声速条件下，来流马赫数越高，往复变形所需要做的功就越小，且伴随着来流马赫数的增大，非定常附加升力导致翼型完成往复变形过程所需对外界做的功对来流马赫数趋于不敏感。而亚声速时，马赫数越高，非定常附加升力将导致完成往复变形需要外界输入的功就越大。

（4）超声速定常流动条件下，尽管升力系数敏感依赖于来流攻角，但翼型完成往复变形所需做的功将不依赖于来流攻角。

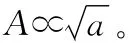
出于数学分析上的方便考虑，本文的数值计算基于可变形儒可夫斯基翼型，另外我们采用了可变形NACA薄翼型进行验证，计算结果均定性相符，本文在此不再进行重复讨论。机翼实行后掠角、弯扭和展弦比等整体式大变形时的超声速气动特性的探讨有待于进一步的研究。

［1］PERRY B，COLE S R，MILLER G D．Summary of an active flexible wing program［J］．Journal of Atrcraft，1995，32（1）：10－15．

［2］CUI E J，BAI P，YANG J M．Development road of smart deformation aircraft［J］．Aeronauttcal Manufacture Technology，2007（8）：38-41．（in Chinese）

崔尔杰，白鹏，杨基明．智能变形飞行器的发展道路［J］．航空制造技术，2007（8）：38-41．

［3］SEIGLER T M，NEAL D A，BAE J S，et al．Modeling and flight control of large-scale morphing aircraft［J］．Journal of Atrcraft，2007，44（4）：1077-1087．

［4］WU J，ANG H S．Aerodynamic characteristics of a folding-wing morphing vehicle［J］．Aeronauttcal Sctence and Technology，2010，2：25-28．（in Chinese））

吴健，昂海松．可折叠翼变形飞行器气动特性研究［J］．航空制造技术，2010，2：25-28．

［5］THEODORSEN T．General theory of aerodynamic instability and the mechanism of flutter［R］．NACA Tech Rep，1935：No．496．

［6］WEIS-FOGH T．Quick estimates of flight fitness in hovering animals，including novel mechanisms for lift production［J］．JExp Bto，1973，59：169-230．

［7］LIGHTHILL M J．On the Weis-Fogh mechanism of lift generation［J］．J Flutd Mech，1973，60：1-17．

［8］MAXWORTHY T J．Experiments on the Weis-Fogh mechanism of lift generation by insects in hovering flight：Part I dynamics of the fling［J］．J Flutd Mech，1979，93：47-63．

［9］SUN M，HAMADANI H．High-lift generation by an airfoil performing unsteady motion at low Reynolds number［J］．Acta Mech．Stntca，2001，17：1-18．

［10］KRAMER M O．Hydrodynamics of the dolphin［J］．Adv．Hydrosct．，1965，2：111-130．

［11］WICKENHEISER M，GARCIA E．Aerodynamic modeling of morphing wings using an extended lifting-line analysis［J］．Jounal of Atrcraft，2007，44（1）：10-16．

［12］NEAL D A，GOOD M G，et al．Design and wind tunnel analysis of fully adaptive aircraft configuration［R］．AIAA Paper 2004-1727．

［13］HALL J，MOHSENI K，LAWRENCE D．Investigation of variable wing-sweep for application in micro air vehicle［R］．AIAA Paper 2005-7171．

［14］SECANELL M，SULEMAN A，GAMBOA P．Design of a morphing aircraft for a light unmanned aerial vehicle using high-fidelity aerodynamic shape optimization［R］．AIAA Paper 2005-1891．

［15］CHEN Q，YIN W L，BAI P，et al．System design and characteristics analysis of a variable-sweep and variablespan wing-body［J］．ACTA Aeronauttcaet Astronauttca Stntca，2010，31（3）：606-613．（in Chinese）

陈钱，尹维龙，白鹏，等．变后掠变展长翼身组合体系统设计与特性分析［J］．航空学报，2010，31（3）：606-613．

［16］CHEN Q，BAI P，YIN W L，et al．Analysis on the aerodynamic characteristics of variable camber airfoils with continuous smooth morphing trailing edge［J］．ACTA Aerodynamtca Stntca，2010，28（1）：46-53．（in Chinese）

陈钱，白鹏，尹维龙，等．可连续光滑偏转后缘的变弯度翼型气动特性分析［J］．空气动力学学报，2010，28（1）：46-53．

［17］GUO Q T，ZHANG L P，CHANG X H，et al．Numerical simulation of dynamic aerodynamic characteristics of a morphing aircraft［J］．ACTA Aerodynamtca Stntca，2011，29（6）：744-750．（in Chinese）

郭秋亭，张来平，常兴华，等．变形飞机动态气动特性数值模拟研究［J］．空气动力学学报，2011，29（6）：744-750．

［18］MORINO L，KUO C C．Subsonic potential aerodynamics for complex configurations：A general theory［J］．AIAA Journal，1974，12（2）：191-197．

［19］MORINO L，CHEN L T，SUCIU E O．Steady and oscillatory subsonic and supersonic aerodynamics around complex configurations［J］．AIAA Journal，1975，13（3）：368-374．

［20］LIU Q G．Review of the Green’s function method for steady and unsteady，subsonic，transonic and supersonic aerodynamics around complex configuration［J］．ACTA Aeronauttcaet Astronauttca Stntca，1996，17（2）：137-143．（in Chinese）

刘千刚．复杂构形的亚、跨、超声速定常及非定常气动力的Green函数计算法综述［J］．航空学报，1996，17（2）：137-143．

［21］ZHOU W B，QIU S G，YAN Z．A boundary element method of supersonic unsteady aerodynamics for wing-tail combination［J］．ACTA Aerodynamtca Stntca，1994，12（1）：100-107．（in Chinese）

周文伯，裘松刚，严震．超声速机翼—尾翼组合体的非定常气动力边界元方法［J］．空气动力学学报，1994，12（1）：100-107．

［22］WANG X H，LAI L J，GAO Y F．Study on the unsteady aerodynamic force of the morphing Joukowski airfoil［J］．Chtnese Quarterly of Mechantcs，2009，30（4）：495-502．（in Chinese）

王晓宏，赖李建，高彦峰．可变形儒可夫斯基翼型非定常气动力的研究［J］．力学季刊，2009，30（4）：495-502．

［23］GAO Y F，WANG X H，LIU Z F．Study on the subsonic unsteady aerodynamic force for the morphing Joukowski airfoil［J］．Chtnese Quarterly of Mechantcs，2012，33（1）：1-9．（in Chinese）

高彦峰，王晓宏，刘志帆．可变形儒可夫斯基翼型亚声速非定常气动力的研究［J］．力学季刊，2012，33（1）：1-9．

［24］TONG B G．Aerodynamics［M］．Beijing：Higher Education Press，1990．（in Chinese）

童秉纲．气体动力学［M］．北京：高等教育出版社，1990．

［25］WANG Y Y．Green function and Navier Stokes equation and its application in ship and ocean engineering［M］．Beijing：National Defence Industry Press，2006．（in Chinese）．

王言英．格林函数与纳维-斯托克斯方程及其在船舶与海洋工程中的应用［M］．北京：国防工业出版社，2006．

［26］CHEN Z C．Partial differential equation［M］．Beijing：Higher Education Press，2003（in Chinese）

陈祖墀．偏微分方程［M］．北京：高等教育出版社，2003．

Study on the supersonic unsteady aerodynamic force for the morphing airfoil

GAO Yanfeng，LIU Zhifan，WANG Xiaohong
（Department of Thermal Science and Energy Engineering，University of Science and Technology of China，Hefei，Anhui 230026，China）

smart aircraft；morphing flight；subsonic flow；aerodynamics force；unsteady flow

V211.41

A doi:10.7638／kqdlxxb-2012.0056

0258-1825（2014）01-0069-08

2012-09-18；

2012-12-19

国家自然科学基金重点基金项目（编号：90816026）

高彦峰（1984-），男，黑龙江兰西人，博士研究生；研究方向：可变形机翼气动特性．E-mail：gaoyf＠mail．ustc．edu．cn

高彦峰，刘志帆，王晓宏．可变形翼型超声速非定常气动力的研究［J］．空气动力学学报，2014，32（1）：69-76．

10．7638／kqdlxxb-2012．0056．GAO Y F，LIU Z F，WANG X H．Study on the supersonic unsteady aerodynamic force for the morphing airfoil［J］．ACTA Aerodynamica Sinica，2014，32（1）：69-76．