基于混合网格的声爆／气动一体化设计方法研究

冯晓强，李占科，宋笔锋，桑建华

（西北工业大学 航空学院，陕西 西安 710072）

0 引 言

超声速飞行时产生的声爆问题已成为新一代军民用超声速飞机研制过程中必须解决的难题。从某种意义上说，声爆问题造成的经济性差导致了“协和式”超声速客机的商业失败。降低超声速客机的声爆水平，使其能够在陆地上空超声速飞行将会给超声速客机带来巨大的潜在市场［1］。

因此，探索声爆预测方法和低声爆布局设计方法已经成为新一代超声速客机发展的当务之急。美国在这一领域已作了较为深入的研究。20世纪70年代末，Seebass等首次提出了基于线化理论Seebass－George－Darden（SGD）方法来降低声爆，为低声爆超声速客机设计奠定了理论基础［2］。在此基础上，Haas等［3］又提出了低声爆超声速客机多激波反设计方法。之后Wu Li等人基于SGD方法和CFD发展了交互式低声爆设计方法［4］。Howel等［5］提出了一种静音锥的低声爆设计概念，通过在机头设置一根可伸缩的静音锥来产生一系列的弱激波，以实现降低声爆的目的，自2006年以来，美国宇航局（NASA）已经对其进行了一系列飞行测试［6］。美国SAI公司联合洛克希德马丁公司的臭鼬工程队一起开展了新一代静音超声速公务机（QSST）的研制计划，已取得实质性进展。日本从1997年开始实施新一代超声速客机研究计划，由日本航空宇航实验室（JAXA）联合高校开展了一系列的研究，2005年在澳大利亚成功实施了基于火箭动力的超声速客机模型飞行试验，2011年在瑞典成功对外形优化低声爆设计方法进行了演示验证。此外欧洲也实施了HISAC计划，对新一代环保型超声速客机涉及到的关键技术展开研究。

国内对于声爆的研究尚处于基础理论探索阶段，文献［7］开展了基于KZK方程的声爆频域预测法，对发动机叶片高速旋转时产生的声爆做了初步研究。文献［8］对超声速公务机的声爆和起降噪声等问题作了初步探讨。文献［9－14］对声爆计算方法以及低声爆设计方法进行了初步研究。

本文探索了基于混合网格的声爆预测方法，在此基础上，对声爆／气动一体化设计方法展开研究。相关分析表明，发动机短舱对超声速升阻特性和声爆特征的影响极为明显，因此开展了发动机短舱位置的声爆／气动一体化设计研究。

1 基于混合网格的声爆预测方法

1.1 声爆预测模型

声爆预测方法是声爆／气动一体化设计方法的基础。将基于CFD的声爆近场预测和基于波形参数法的声爆远场预测相结合构建了声爆预测方法，主要分为以下三步：首先，对飞机近场区域进行求解，通过求解NS方程或者欧拉方程得到近场激波结构和压力扰动；其次，将从近场提取的压力分布作为声爆远场计算的初始条件，利用波形参数法计算得到地面声爆波形；最后，计算声爆信号的感觉噪声级PLdB。图1为声爆预测模型。

图1 声爆预测模型Fig.1 Sonic boom prediction model

波形参数法的基本原理如图2所示［15］，通过分段的方式利用一系列的参数来描述声爆信号在大气中的传播。其中第i段信号的持续时间为λi＝Ti＋1－Ti，压强随时间的变化率为 mi＝（pi－pi－1）／λi，通过激波后的压强增量为Δpi＝pi－pi－1。

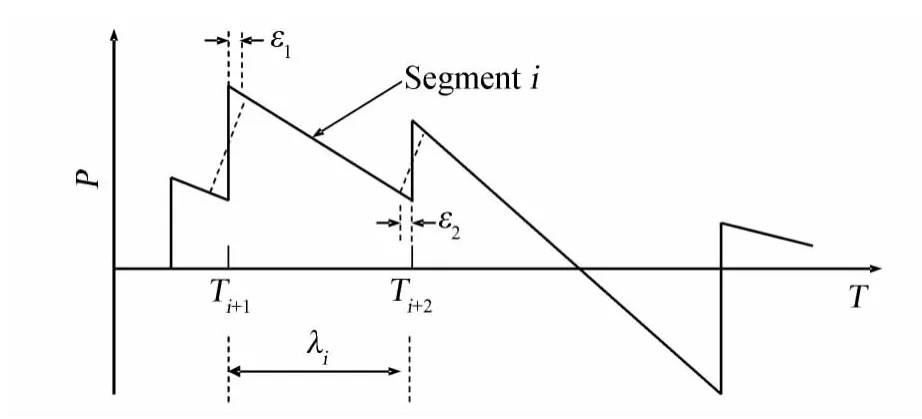
图2 波形参数法Fig.2 Waveform parameter method

在小扰动假设条件下，波形参数法的解为：

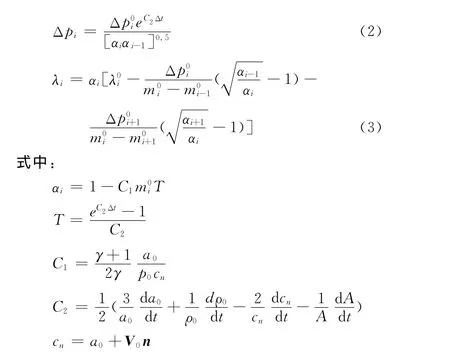
其中，下标0代表滞止值，上标0代表上一步的迭代值，a0代表声速，V代表风速，n代表单位法向波前，A代表声线管截面积，e是自然对数的底数，cn代表声波传播的法向速度。

基于上述波形参数法开发了F－BOOM声爆计算程序，图3为F－BOOM计算得到的远场声爆值与F104战斗机飞行试验值的比较［16］，计算条件设定为：飞行高度8534m，飞行马赫数1.5，采用标准大气模型。由图可知，基于波形参数法的远场声爆计算方法可以满足声爆远场计算的精度要求。

图3 地面声爆计算值与飞行试验值比较Fig.3 Ground sonic booms comparision between calculation and flight test

1.2 基于结构／非结构网格的声爆近场预测方法

常规的声爆近场预测采用结构化网格，可以对近场激波进行精确捕捉。但是，对于飞行器复杂外形而言结构化网格需要花费大量的时间生成，效率和网格质量低下。而非结构网格则对复杂外形具有很好的适应性，但非结构网格不能很好的对激波进行精确捕捉。因此，将结构化网格与非结构化网格进行接合，综合利用结构化网格计算效率高和非结构化网格对复杂外形适应性好的优势，实现对声爆近场的精确预测。

用于声爆近场预测的结构／非结构混合网格拓扑结构如图4所示，在飞机近壁面附近采用非结构网格，而在外部则利用结构化网格，计算域采用楔形拓扑结构，楔形角与马赫角相同。

图4 基于混合网格的声爆近场预测拓扑结构Fig.4 Sonic boom near field prediction topology based on structured／unstructured hybrid method

图5为基于混合网格的声爆预测流程，首先生成飞机气动外形和结构／非结构分界面；其次，在分界面内生成非结构网格，在分界面外生成结构化网格；第三，对结构化网格和非结构化网格进行接合；第四，对流场进行求解，判断激波捕捉精度是否满足要求，若不满足，重新划分网格；最后，提取近场压力分布，利用波形参数法计算声爆远场信号。

图5 基于混合网格的声爆预测流程Fig.5 Flow chart of sonic boom prediction method based on structured／unstructured hybrid grid

国外研究表明，声爆近场计算采用欧拉方程可以满足精度需求［17］，近场采用混合网格，二阶迎风格式，时间推进采用Runge－Kutta法得到稳态解。当需要考虑粘性时，则在飞机近壁面生成棱柱体网格，并且求解NS方程。图6为NASA TND－3106文献［18］风洞试验示意图，风洞试验模型如图所示，其圆锥半径r的分布如图所示。图7为计算数据和风洞试验数据的比较，设定马赫数为1.41，总压69kPa，总温311K，与风洞试验条件相同。图中黑色实线为采用各项同性的结构化网格的计算结果，黑色虚线为混合网格的计算结果，由计算结果可知，结构化网格的计算精度比混合网格的计算精度略高，但基于混合网格的声爆近场预测方法仍然可以满足声爆近场预测的精度需求。

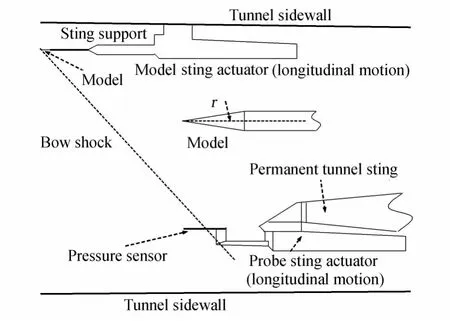
图6 文献TND－3106风洞试验示意图Fig.6 Illustration of wind tunnel experiment of TND－3106

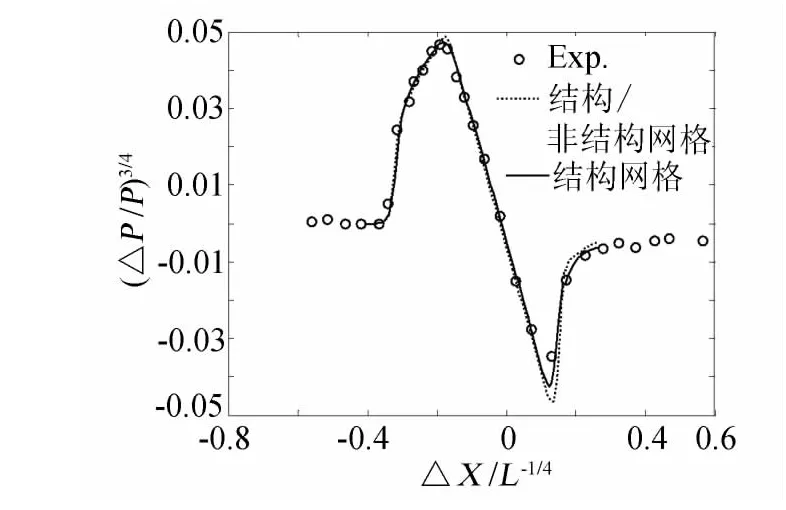
图7 计算值与风洞试验值对比Fig.7 Results comparison between the experiment data and the calculation results

1.3 远近场匹配方法

声爆计算中远近场的定义并不是固定的，而是根据实际问题而变化的。声爆远场计算采用的波形参数法本质上是一种线化方法，远近场的匹配直接影响地面声爆的计算精度。假设L代表飞机的长度，H代表距离飞机的径向距离，如图8所示，因此不同的H L值代表了不同的声源位置和远场计算的匹配距离。如果H／L值太小，远近场匹配不足，近场非线性效应导致远场计算错误；如果H／L值太大，导致计算需要的网格量激增，从而导致计算成本急剧上升。Plotkin提出了若干种远近场匹配方法［19］，但都比较复杂。本文采用直接匹配法实现声爆远近场的匹配［20］，设Δp为声爆扰动压强，p为未扰动的大气压强。超声速线化理论表明，压力扰动Δp／p随的增加而减小，因此，当压力扰动随匹配距离的增加开始减小时，可以认为此时近场非线性效应已经很弱，远近场的匹配是成功的。图8为从不同匹配距离提取的声爆近场压力分布。图9为声爆超压值和匹配距离的关系，由图可知，对于所要解决的问题，H／L≥2.5时超压值开始呈现减小的趋势，因此，匹配距离H／L＝2.5是满足要求的。

图8 声爆远近场匹配Fig.8 Sonic boom far field and near field match

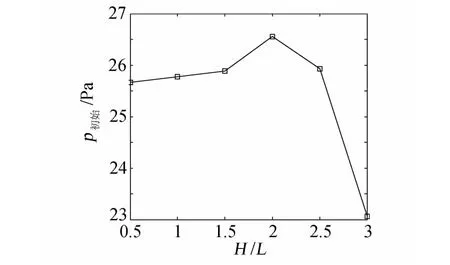
图9 由不同匹配距离计算得到的地面声爆初始超压值Fig.9 Ground sonic boom initial pressure obtained from several H／L

2 声爆／气动一体化设计方法

2.1 响应面模型

响应面模型［21］是以统计方法和数学方法为基础，通过近似构造一个具有明确表达形式的多项式来表达隐式功能函数，本质上来说响应面法是一套统计方法。通常使用低阶多项式构造响应面，形式如下：

式中：N为设计变量个数，xi为设计变量。

2.2 Pareto遗传算法

声爆气动一体化设计是一个多点设计问题，多目标优化问题可以描述为：

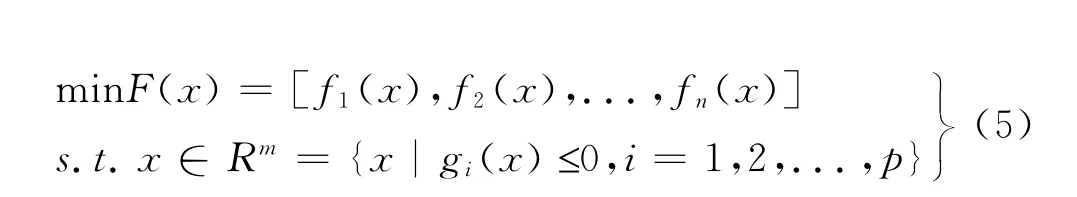
Pareto方法通过求解优化问题中的非劣解集［22］，从而获得不同目标偏向情况下的一组优化解集。对于声爆／气动一体化设计，利用Pareto多目标优化能一次性给出不同设计目标偏向下的优化解集。Pareto解定义为：假设U，V∈Rm，如果不存在可行解U，使得

则V为Pareto解。

2.3 试验设计方法

在基于响应面模型的多目标优化设计中试验设计是其关键之一，试验设计的好坏直接影响模型的近似程度，也影响着设计变量的最终寻优结果。拉丁超立方抽样（LHS）［23］是一种广泛应用于计算机仿真试验设计的方法。

2.4 声爆／气动一体化设计流程

图10给出了基于声爆预测方法、响应面模型以及Pareto遗传算法的声爆／气动一体化设计流程，流程主要包括：试验设计、声爆水平及升阻特性计算、响应面模型建立、Pareto多目标优化以及优化方案确定等。

通过拉丁超立方抽样对发动机短舱位置构成的设计空间进行采样，计算中对发动机短舱展向位置和弦向位置两个参数进行组合，构造了19组样本方案。利用声爆预测方法对构造的样本方案的声爆水平和升阻特性进行计算分析。

3 梭式布局短舱位置优化

文献［10］提出了一种梭式布局超声速客机方案，可以较好地兼顾气动性能和低声爆特征。在梭式布局的基础上开展发动机短舱位置的声爆／气动一体化设计研究。

3.1 梭式布局声爆／气动特性分析

计算条件设定为：马赫数1.41，飞行高度14km，温度216.5K，压力14000Pa。图11为0°迎角时翼身组合体和带发动机短舱的布局的地面声爆信号比较，由图可得，增加短舱后地面声爆超压值增大了23.5%，升阻比降低了34%，因此，发动机短舱对超声速客机的声爆水平和升阻特性都有极大的影响。有必要开展针对发动机短舱的声爆气动一体化设计研究。

图10 声爆气动一体化设计流程Fig.10 Flow chart of optimization of sonic boom and aerodynamic performance

图11 翼身组合体和带发动机短舱的布局声爆信号比较Fig.11 Sonic boom signatures comparison between the wing body and the nacelle layout

图12为梭式布局方案在马赫数1.41时升阻比和声爆超压值随迎角的变化曲线，由图可知，梭式布局方案在超声速巡航状态下有较好的升阻特性和较低的声爆水平，因此在梭式布局的基础上开展声爆气动一体化设计方法研究具有更大的工程实用价值。

图12 声爆超压值和升阻比随迎角的变化曲线Fig.12 Sonic boom overpressures and lift to drag ratio obtained from different angles of attack

3.2 发动机短舱位置优化

图13为发动机短舱位置坐标系以及相应坐标的取值范围，主要对发动机短舱在机翼上的安装位置进行优化，优化目标为超声速升阻比和地面声爆水平。

图13 发动机短舱位置参数Fig.13 Parameters of nacelle location

通过响应面法构造声爆超压值和升阻比的代理模型。图14为构造得到的声爆超压值响应面模型。

图14 声爆超压值响应面模型Fig.14 Response surface model of sonic boom overpressure

声爆／气动一体化设计通过Pareto遗传算法在响应面模型上进行多目标优化。利用非支配排序遗传算法（NSGA－II）对发动机短舱位置参数进行多目标优化设计，初始种群数为100，进化代数20。与其他多目标优化算法相比，该算法具有更强的Pareto前沿前进能力，同时在进化过程中能够防止早熟收敛，保证种群的分布多样性。图15为经过遗传算法优化得到的Pareto解集，横坐标和纵坐标分别为超声速升阻比和地面声爆超压值。

图15 Pareto前沿解集与优化解Fig.15 Pareto solutions and optimized layout

3.3 优化结果及分析

由图15可知，多目标优化得到的Pareto前沿解集是两个设计目标之间不同偏向下的优化解的集合，优化中基本没有其他可行解在两个设计目标上能同时比Pareto解更好。声爆／气动一体化设计中，Pareto解集代表了所有最优方案的集合，因此优化方案可以根据设计偏向直接在Pareto解集中选择。根据突出超声速升阻比、超声速升阻比和降低声爆兼顾以及突出低声爆性能3种不同的设计偏向，在图15所示的Pareto解集中选择了3种方案作为最终的设计结果。

图16为3种优化方案和原始设计方案的压力分布图。优化方案1为突出了超声速升阻比的方案，优化方案2为超声速升阻比和低声爆兼顾的方案，优化方案3为突出低声爆特征的方案。

表1给出了对于优化解响应面模型和CFD声爆预测结果的比较，由表可知，对于两个设计目标，响应面模型和CFD计算方法的计算偏差均小于5%，能够满足声爆／气动一体化设计的需要。

表1 响应面模型结果与CFD结果比较Table 1 Results comparison between the RSM and the CFD solutions

表2为三种优化方案与原始方案在设计目标上的比较，方案1侧重于优化超声速升阻比，方案2兼顾低声爆和超声速升阻比，方案3侧重优化低声爆。由表可知，对于所选定的设计偏向，优化方案较原始方案都有不同程度的性能提升。

图16 原始方案与优化方案比较Fig.16 Comparison between the original layout and the optimized layouts

表2 原始方案与初始方案性能比较Table 2 Variation of performance between the original layout and the optimized layouts

由以上分析可知，优化方案1与原始方案相比，升阻比增大26.34%，但声爆增加11.45%；优化方案2与原始方案相比，升阻比增大8.46%，声爆超压值降低4.72%；优化方案3与原始方案相比，升阻比下降13.04%，声爆超压值降低20.62%。

另外，从表2中也可以看出，在声爆／气动一体化设计时，没有对两个目标绝对最优的方案，偏向其中一个设计目标必然牺牲另一个目标的性能。在同样的设计偏向下，经过Pareto优化方案的性能要优于其他可行方案。

4 结 论

探索了基于混合网格的近场预测以及基于波形参数法的远场预测的声爆预测方法，综合利用了结构化网格计算效率高以及非结构网格对复杂外形适应性好的优点，在保证声爆预测精度的基础上提高了计算效率。

建立了基于声爆预测方法、响应面模型和Pareto遗传算法的声爆／气动一体化设计方法。

利用声爆／气动一体化设计方法对发动机短舱位置进行了一体化设计研究。结果表明，优化方案1偏向增加超声速升阻比，与原始方案相比，升阻比增加26.34%；优化方案2兼顾增加超声速升阻比和降低声爆，优化方案与原始方案相比，升阻比增加8.46%，声爆超压值降低4.72%；优化方案3侧重降低声爆，优化方案与原始方案相比，声爆超压值降低20.62%。

［1］NATIONAL RESEARCH COUNCIL.High speed research aeronautics and space engineering board U.S.supersonic commercial aircraft：assessing NASA′s high speed research program［R］.National Academy Press，Washington，D.C.，1997.

［2］SEEBASS A R.Sonic boom theory［J］.Journal of Aircraft，1969，6（13）：177－184.

［3］HAAS A，KROO I.A multi－shock inverse design method for low－boom supersonic aircraft［R］.AIAA －2010－843，2010.

［4］LI W，SHIELDS E，LE D.Interactive inverse design optimization of fuselage shape for low－boom supersonic concepts［J］.Journal of Aircraft，2008，45（4）：1381－1398.

［5］HOWE D C.Improved sonic boom minimization with extendable nose spike［R］.AIAA－2005－1014，2005.

［6］DONALD FREUND，FRANK SIMMONS.Quiet spikeTMprototype flight test results［R］.AIAA－2007－1778，2007.

［7］陈鹏，李晓东.基于 Khokhlov－Zabolotskaya－Kuznetsov方程的声爆频域预测法［J］.航空动力学报，2010，25（2）：359－365.

［8］ 但聃.基于声爆和起降噪声要求的超音速公务机设计［D］.［硕士学位论文］.中国航空研究院611所，2010：31－35.

［9］冯晓强，李占科，宋笔锋.超音速客机音爆问题初步研究［J］.飞行力学，2010，28（6）：21－27.

［10］冯晓强，李占科，宋笔锋.超声速客机低音爆布局反设计技术研究［J］.航空学报，2011，32（11）：1980－1986.

［11］冯晓强.声爆计算方法研究及在超声速客机设计的应用［D］.［硕士学位论文］.西北工业大学，2012：43－53.

［12］冯晓强，宋笔锋，李占科.低声爆静音锥设计方法研究［J］.航空学报，2013，34（5）：1009－1017.

［13］冯晓强，宋笔锋，李占科，等.超声速飞机低声爆布局混合优化方法研究［J］.航空学报，2013，34（8）：1768－1777.

［14］沈沉，周华.细长杆降低超声速客机气动噪声的数值分析［J］.空气动力学学报，2012，30（1）：39－45.

［15］THOMAS C L.Extrapolation ofsonic boom pressure signatures by the waveform parameter method［R］.NASA TND－6832，1972.

［16］TIMOTHY P J.Comparison of sonic booms from modified linear theory to flight test data［R］.AIAA－2012－0018，2012.

［17］ISIK ALI O.Sonic boom prediction using Euler／full potential methodology［R］.AIAA－2007－0369，2007.

［18］CARLSON H W.A wind tunnel investigation of the effect of body shape on sonic boom pressure distributions［R］.NASA TND－3106，1965.

［19］KENNETH J P.Extrapolation of sonic boom signatures from CFD solutions［R］.AIAA－2002－0922，2002.

［20］KANDIL O A.Prediction of sonic boom signature using Euler－full potential CFD with grid adaptation and shock fitting［R］.AIAA－2002－2542，2002.

［21］张成成.基于响应面的结构抗疲劳优化设计方法［D］.［硕士学位论文］.南京航空航天大学，2007：10－12.

［22］梁煜，程小全，郦正能.基于代理模型的气动外形平面参数多目标匹配设计［J］.航空学报，2010，31（6）：1141－1148.

［23］刘继涛，刘飞，张为华.基于拉丁超立方抽样及响应面的结构模糊分析［J］.机械强度，2011，33（1）：073－076.