自由活塞激波风洞定压驱动时间研究

朱 浩，沈 清，宫 建

（中国航天空气动力技术研究院，北京 100074）

自由活塞激波风洞定压驱动时间研究

朱 浩，沈 清，宫 建

（中国航天空气动力技术研究院，北京 100074）

自由活塞激波风洞是一种高焓值的高超声速地面试验设备，其运行时间十分短暂。提高自由活塞激波风洞有效试验时间的一个可行途径是延长定压驱动时间。以此为目的，本文探索了活塞压缩器中活塞速度对定压驱动时间的影响。研究结果表明，在不同的初始参数下，定压驱动时间关于活塞速度存在极大值，这些极大值形成了一条脊线（局部极值曲线）。随后，通过数值计算的结果归纳出脊线的若干性质。这些结果表明，在活塞压缩器的理论设计中，设计参数应选择在靠近这条脊线的区域，并且该处的定压驱动时间关于参数的梯度应该相对较小。

自由活塞激波风洞；活塞压缩器；定压驱动时间；脊线

0 引 言

自由活塞激波风洞是一种采用活塞压缩器作为驱动装置的激波风洞。这类风洞可以产生和近地轨道飞行器的焓值相当的高能量试验气流，足以使得试验气体分子发生离解和电离，因此可以复现高超声速飞行中出现的真实气体效应。自由活塞激波风洞被人所知，源于“Stalker管”（即利用活塞压缩器推动的激波管），这是Stalker在20世纪60年代尝试着从激波风洞技术上去理解真实气体效应而获得的产物。随着建造高超声速飞行器兴趣的增长，澳大利亚、美国、德国以及日本开始陆续兴建了这类自由活塞激波风洞。关于这类风洞的评述文章可参阅文献［1］。

活塞压缩器是自由活塞激波风洞的核心部件之一。活塞压缩器的性能决定了自由活塞激波风洞的驱动能力。20世纪60年代，Stalker率先对于这类活塞压缩器的进行理论研究［2-3］，并开展了相关工程实践。20世纪80年代后期，Hornung进一步完善了活塞压缩器中活塞运行的理论刻画［4］。受到Stalker活塞软着陆思想的启发，Itoh等人将活塞运动学方程近似为一个Bessel方程，给出了调谐操作（tuned operation）满足的条件。在此条件下，活塞可以在膜片破裂以后保持一定速度实现定压驱动，同时还将柔软地停在压缩管的末端，不发生碰撞［5］。近些年来Jacobs等人采用CFD手段模拟了自由活塞激波风洞的运行，探索了摩擦、热损失和气体泄漏对活塞运动的具体影响［6］。活塞压缩器的相关试验研究见文献［7-8］。基于Hornung的活塞运动学方程，本文详细地探索了参数空间上活塞速度和定常驱动时间的关系，这可以看作是对Hornung和Itoh等人的理论研究工作的一个补充。

事实上，自由活塞激波风洞的有效试验时间是短暂的，一般在几个毫秒以内。在实际运行中，自由活塞激波风洞的有效试验时间受到多种因素的影响。理论设计中，拓展定压驱动时间（或者称为常压力时间），采用缝合操作是延长自由活塞激波风洞有效试验时间的主要途径。为了理论研究的方便，本文将自由活塞激波风洞简化为“Stalker管”，通过研究了“Stalker管”中活塞速度对定压驱动时间的影响，获得了定压驱动时间的极值曲线及其相关性质。这将为寻找合适的活塞破膜速度（膜片在预设压力下破裂时，活塞具有的运行速度［4-5］），获得最优或者次优的定压驱动时间提供便利。

1 活塞的控制方程

自由活塞激波风洞的运行如图1所示，在压缩管中，重活塞的右侧为驱动气体（一般为氦气或者氦气和氩气的混合气体，为了研究方便，本文选用氦气作为驱动气体），其压力很低，在重活塞的左侧，连接高压空气贮室，其内贮存高压空气。当释放活塞时，由于活塞两边压力存在巨大差别，活塞向低压气体的方向加速运动，低压气体从膨胀的高压气体那里获得能量，当活塞抵达压缩管的末端时，活塞逐步减速，到达预设压力时，膜片破裂，激波管处于启动状态。这个压缩过程可以使得氦气具有很高的压力和温度（比如在一个典型状态下，氦气的压力和温度分别为20MPa和4000K）。膜片破裂以后，活塞仍然向前运动，速度继续减小。

图1 自由活塞激波风洞的运行（取自文献［6］）Fig.1 The operation of the free piston tunnel

由于采用重活塞，驱动气体的压缩过程可以视为等熵压缩。氦气密度小声速大，作为驱动气体特别适合。此外，在较高的温度下，氦气仍然可以保持完全气体性质。当自由活塞激波风洞在缝合接触面模式下运行时，试验时间依赖于活塞在压缩管末端的停止方式。因此，在膜片破裂以后，控制活塞移动减缓驱动气体压降时间对风洞的延长有效试验时间十分有益。这也就是本文研究定压驱动时间的原因所在。

在本文的研究过程中将不考虑摩擦和气体泄漏。破膜以前，无量纲化的活塞运动方程可以表示为如下形式（具体推导过程，见文献［4］）：

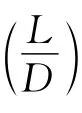
膜片破裂之后的运行机制如下，活塞到达设定的压缩位置时，膜片达到设定的极限压力，随即发生破裂。此后活塞仍然保持原来的运动方向向下游运动，继续推动氦气，使其扩张进入激波管。假定膜片的破裂过程是个瞬态过程，仿照方程（1）做无量纲处理后，可以得到（具体推导过程，见文献［4］）：

方程组（2）中变量μ＝m／mr表示破膜以后氦气的无量纲质量。方程组（2）边界条件为：

这里

其中，pAr表示破膜时刻高压空气的压力，pr表示破膜时刻氦气的压力，ξr表示破膜时刻活塞的无量纲位置。以上参数除了b5是新参数以外，其他两个b3和b4均可以用b1和b2加以表达。如果自由活塞激波风洞的压缩管和激波管的尺寸给定，那么b5为确定量。以下的研究工作主要将在参数空间（b1，b2）上进行。

自由活塞激波风洞的采用的压缩比λ一般控制在40～60之间。于是，膜片破裂时刻活塞的无量纲位置可以表达为：

2 定压驱动时间的确定

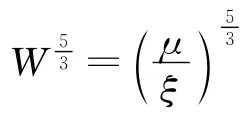
将破膜时刻作为定压驱动的起点，上述的定压驱动时间可以表述成如下的数学过程。首先利用

获得τmax。再利用如下方程获得：

这样一来，定压时间可以表示为：

假定膜片在固定的压缩比λ下破裂，那么氦气以声速条件流进激波管。当活塞速度刚好抵消氦气的排出体积，压缩管末端的氦气压力将保持定常值。此时，活塞具有的速度称为临界速度φrc，其具体表示如下：

为了获得更长的定压驱动时间，活塞正常的破膜速度一般将高于这个临界速度［4，9］。但是过快的活塞的破膜速度不仅对定压驱动时间不利，而且也增加了活塞软着陆的困难。因此研究不同运行参数下的活塞的破膜速度，对风洞的气动设计是有益的。不过，众多的参数使得获得破膜速度和定压驱动时间的直接关系十分困难。

图2 定压驱动时间的定义Fig.2 Definition of the constant pressure time

3 活塞控制方程的重整化

为了详尽研究破膜速度对于定压驱动时间的影响，需要将方程（2）做如下的重整化变换。

经过重整化以后，方程（9）将会给理论研究和计算带来很大方便，此时各个变量的初始值均为1，其演化过程如图3所示。

图3 活塞的速度、位置以及氦气的质量和压力随时间的演化（其中参数b1＝0.01，b2＝25.0，b5＝0.5，Fig.3 Velocity，position of the piston and mass，pressure of driver gas（He）with dimensionless time

由于氦气的无量纲质量Z是随无量纲时间τ单调递减的，于是τ可以用Z加以代替，即τ＝τ（Z）。另外，方程（9）的其他两个变量X、Y也可以表示成质量μ的函数。但是，直接找出这样的显式函数表达仍然困难［10］，文献［5，11］采用Bessel方程理论获得了近似的显式表达，可供参阅。选择μ代替τ，将会在定压驱动时间的极值研究中带来便利。

4 定压驱动时间极大值的存在性

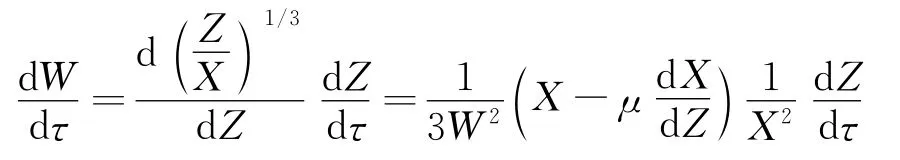
上式的物理意义相当明显。当活塞的破膜速度φr大于破膜临界速度φrc时（即β＞1），活塞对于压缩管末端的空气继续进行压缩，其压缩管中的压力还将增加，当破膜速度φr下降到临界速度φc的时刻，压缩管末端压力抵达最大值，在这个时刻，密度信息W满足：

化简之后得到：

这就是密度信息极值和活塞速度之间的关系。相应地，对应的峰值压力为：

如果将破膜时刻作为定压驱动的起点（后面的数值结果可以证实这样的假设是合理的）。由于τ可以表示为Z的函数，利用方程组（9）可知，定压驱动时间τcp是Zsub的函数，而Zsub满足

上式中，Zmax表示压力获得极大值时刻下的Z，而τ（Zsub）对应着定压驱动结束时刻。W－1表示压力信息W的反函数。对方程（13）的第一个等式，利用隐函数定理，可以得到，定压驱动时间关于参数b2（或者b1）存在极值，即可考虑

而在上式中

这里（*）＝［（0．9）1／3W（τ（Zmax））］。由于τ是Z的函数，上式表明定压驱动时间τcp关于参数b1或者b2均存极大值。因此，定压驱动时间τcp的图像关于坐标参数b1和b2存在着一条脊线（局部极大值线），如图4所示。

图4 活塞定压驱动时间和活塞速度在平面（b1，b2）上的分布（其中参数Fig.4 Distribution of the constant pressure time and piston velocity on the plane（b1，b2）

与此同时，活塞的破膜速度φ（或者β）亦由参数b1、b2决定。这样以来，定压驱动时间的极值曲线也将和活塞速度变化曲线形成对应，定压驱动时间极值下的最优活塞速度由此得到。

5 脊线的重要性质

脊线的存在性和唯一性，意味着定压驱动时间τcp关于活塞速度β存在极值。在图4中，将脊线向下投影到活塞速度β的曲面上，即可获得活塞破膜速度β的极值曲线。这条曲线刻画了定压驱动时间τcp取得局部最大值时，活塞具有的破膜速度β。一般而言，自由活塞风洞的活塞破膜速度的选择应该尽可能从外侧靠近这条极值曲线（极值曲线的外侧β相对较小）。这样选择的好处在于定压驱动时间τcp变化相对平缓（如图4），且更有可能实现调谐操作。

图5 活塞速度等值面上的极值曲线Fig.5 Extremely curves in the velocity distribution on the plane（b1，b2）

表1 极值曲线上若干重要变量值（不同压缩比）Table 1 Important quantities of ridge curve with different compress ratio

表2 极值曲线上若干重要变量值（不同设计参数）Table 2 Importantquantities of ridge curve with different design parameters

图6 极值曲线（脊线）上无量纲压力比的变化（L／d＝70，D／d＝3.3，λ＝50）Fig.6 Dimensionless pressure ratio of the ridge curve

6 结 论

在高超声速飞行中，真实气体效应对于飞行器的气动力／热影响显著，由于目前CFD手段的局限性，对真实气体效应的研究主要还是依赖地面试验。虽然，自由活塞激波风洞产生的试验气流在离解度和组分上，与真实飞行环境还存在一定偏差，但就目前技术水平而言，自由活塞激波风洞仍然是研究真实气体效应的重要地面设备之一。这类风洞有效运行时间十分短暂，延长风洞的活塞压缩器的定压驱动时间将有助于弥补这一缺陷。本文以此为目的，利用重整化方程，证明了定压驱动时间的局部极值曲线（即脊线）的存在性，并详尽地研究了活塞破膜速度和定压驱动时间的关系。通过脊线在速度分布曲面上的投影，获得了最优的活塞破膜速度的极值曲线。辅以数值计算，本文获得了不同设备参数下的极值曲线的若干重要性质。这些结果将为调谐操作约束下的设计点的选择，提供了更为准确和有效的理论依据。

［1］STALKER R J．Modern developments in hypersonic wind tunnels［J］．The Aeronauttcal Journal，2006，110：21-39．

［2］STALKER R J．The free piston shock tube，Aero．Quart．17［M］．1966．

［3］STALKER R J．A study of the free piston shock tunnel［J］．AIAA Journal，1967，5：2160-2165．

［4］HORNUNG H G．The piston motion in a free piston driver for shock tubes and tunnels［R］．GALCIT Rep．FM88-1，1988．

［5］ITOH K，et al．Improvement of a free piston driver for a high enthalpy shock tunnel［J］．Shock Wave，1998，8：215-233．

［6］JACOBS P A．Quasi-one-dimension modeling of free piston shock tunnel［R］．AIAA 93-0352，1993．

［7］LABRACHERIE L，et al．On compression process in a free piston shock tunnel［J］．Shock Wave，1993，3：19-23．［8］TANNO H，ITOH K，SATO K．Experimental study on the tuned operation of a free piston driver［J］．Shock Wave，2000，10：1-7．

［9］GAI S L．Free piston shock tunnels：developments and capabilities［J］．Prog．Aerospace Sct．，1992，29：1-41．

［10］FARRELL O J，ROSS B．Solved problems in analysis as applied to Gamma，Beta，Legendre，Bessel functions［M］．New York：Dover publications，1971．

［11］LUKE Y L．Mathematical functions and their approximations［M］．New York：Academic Press，1975．

The constant pressure time of piston driver in free piston shock tunnel

ZHU Hao，SHEN Qing，GONG Jian
（China Aerospace Aerodynamics Academy，Beijing 100074，China）

The free piston shock tunnel is one of high-enthalpy ground facilities for hypersonic test，however the useful test time of this kind tunnel is very short．Increasing the constant-pressure time of piston driver can be regarded as one of the available approach to extend the useful test time of the free piston shock tunnel．For this reason，the relation of the piston velocity and the constant-pressure time in the piston driver was studied in this paper．The results revealed that the constant-pressure time has local maximums with different velocity of piston and initial parameters，which form a ridge curve．Subsequently，the properties of this ridge curve were obtained by numerical analysis．It shows that the optimal or suboptimal design points of this tunnel should be close to the ridge curve，and its gradient of constant-pressure time is small．

free piston shock tunnel；piston driver；constant-pressure time；ridge curve

V211.751

A doi:10.7638／kqdlxxb-2012.0048

0258-1825（2014）01-0045-06

2012-11-14；

2013-06-07

朱 浩（1977-），男，江苏邳州人，高级工程师，研究方向：高超声速空气动力学．E-mail：zhuhao1977＠hotmail．com

朱 浩，沈 清，宫 建．自由活塞激波风洞定压驱动时间研究［J］．空气动力学学报，2014，32（1）：45-50．

10．7638／kqdlxxb-2012．0048。ZHU H，SHEN Q，GONG J．The constant pressure time of piston driver in free piston shock tunnel［J］．ACTA Aerodynamica Sinica，2014，32（1）：45-50．