覆冰四分裂导线节段模型驰振风洞模拟试验

严 波，刘小会，胡 景，周 松，张宏雁

（1.重庆大学 资源及环境科学学院，重庆 400030；2.四川省电力工业调整试验所，四川 成都 610016；3.四川电力科学研究院，四川 成都 610071）

0 引 言

覆冰导线的舞动可能导致相间闪络、断线甚至杆塔倒塌等事故，是输电线路安全运行中急需解决的关键问题之一。目前，对这一问题的研究已受到广泛关注。覆冰导线舞动的研究主要包括舞动机理、数值模拟和覆冰导线气动特性及舞动试验研究等。舞动机理研究方面，最早出现的有Den Hartog垂直舞动机理和O Nigol扭转舞动机理［1］，之后又发展了多种耦合舞动理论和稳定性理论［1－2］。舞动数值模拟研究方面，也取得了不少研究成果［3－6］。

关于覆冰导线气动特性的风洞试验研究起步较早，但国际上公开报道的试验数据却非常有限［7］。近年，国内学者对典型覆冰三分裂导线和四分裂导线的气动特性进行了一系列的风洞试验研究，获得了宝贵的试验数据［8－10］。此外，国际上日本和加拿大等国较早建立了试验线路用于观测和研究输电线路的舞动［11－12］。2008年，我国国家电网公司在河南省郑州尖山建立了我国第一条真型输电试验线路，并于2011年6月在导线上安装D形人造覆冰模型后诱发了舞动。利用试验线路研究舞动问题存在重复性差、效率低、在现场不易准确获取各种数据的缺点，不便于理论和数值方法的验证以及参数研究等。另一方面，若利用风洞试验模拟覆冰导线的舞动，则要求结构气动弹性模型的设计满足相似性原理。文献［13］提出了建立输电导线风洞试验气动弹性模型的方法，并对双分裂导线的气动弹性问题进行了风洞试验研究［14］。然而，对于覆冰导线，要设计满足相似性原理的气动弹性模型却极为困难，特别是要同时满足阻力、升力和扭矩的相似性几乎不可能。因此，基于输电导线大档距小弧垂的特点，文献［7］采用导线节段模型，在风洞中模拟了一种实际冰形覆冰单导线的驰振过程。目前，尚未见到覆冰分裂导线舞动模拟的风洞试验研究报道。

本文采用覆冰导线节段模型，针对典型的新月形和扇形冰型，利用风洞试验模拟覆冰四分裂导线节段模型的驰振，并利用作者提出的舞动数值模拟方法［5］模拟风洞试验，进而对数值方法进行验证。试验结果对输电线路舞动问题的研究具有重要的价值。

1 覆冰导线节段模型驰振试验原理

对于覆冰导线，要设计同时满足阻力、升力和扭矩相似性的气动弹性模型还难以实现，这也是目前还没有输电线舞动风洞模拟试验研究报道的原因。尽管如此，根据输电导线大档距小弧垂的特点，可以采用覆冰导线节段模型，在风洞中模拟其驰振过程，试验结果可以用于验证覆冰导线舞动方法的正确性。若利用节段模型，覆冰导线可以采用和原型相同的截面尺寸，即缩尺比为1，因而可以不考虑相似性问题。

1.1 覆冰形状及导线型号

新月形和扇形覆冰是输电线路中两种常见的形式，该两种覆冰导线的截面示意图如图1所示。节段模型驰振风洞模拟试验中新月形覆冰的厚度取28mm，扇形覆冰的厚度取18mm。

四分裂导线为钢芯铝绞线，型号为4XLGJ－400／50。每根子导线的直径为27.6mm，相邻子导线的间距为450mm。

1.2 试验原理

覆冰四分裂导线节段模型驰振风洞模拟试验原理参见图2所示。四根覆冰子导线模型的两端固定在两个竖直圆盘上。覆冰导线模型由四根竖直弹簧悬挂起来，另用四根弹簧约束试验模型在水平方向的运动。可通过改变弹簧的刚度和悬挂点调整模型的垂直、水平和扭转刚度，还可通过调整配重块在吊架上的位置改变模型的转动惯量，从而改变系统的固有频率。系统的固有频率可用模态分析系统测得，该系统包括加速度传感器、数据采集器和动态信号分析仪。

图1 覆冰导线模型截面示意图Fig.1 Cross－section of iced conductor model

图2 覆冰四分裂导线节段模型驰振风洞试验原理示意图Fig.2 Mechanism of wind－tunnel test for galloping of iced quad bundle conductor

在分裂导线节段模型的一端部安装三个均匀排列的LED点光源，分别用三个CCD摄像机记录该三个光点的运动轨迹，通过数据采集系统，由计算机记录导线节段模型的垂直、水平位移随时间的变化以及导线模型的驰振运动轨迹。

2 覆冰导线驰振风洞模拟试验

2.1 覆冰四分裂导线试验模型

为了尽量与实际接近，导线模型为外表面盘绕橡胶管的中空硬铝管，橡胶管用于模拟绞股线。导线模型的外径与实际导线相同，每根子导线模型的直径为27.6mm，长度取1300mm。覆冰模型则采用与冰密度接近的轻木制作，将其附着在导线模型上。相邻子导线的间距为450mm，四根子导线模型的两端固定在两个竖直薄圆盘上。

覆冰导线试验模型如图3所示，图3（a）和（b）所示分别为新月形覆冰子线和扇形覆冰子导线模型；图3（c）所示为水平安装在风洞内的覆冰四分裂导线节段模型。

图3 覆冰四分裂导线试验模型Fig.3 Test model of iced quad bundle conductor

2.2 试验系统

试验在中国空气动力研究与发展中心低速空气动力研究所1.4m×1.4m风洞中完成。该风洞为直流式低速风洞，截面形状为切角矩形，试验段长2.8m，风速范围为0～65m／s。

图4所示为覆冰四分裂导线节段模型驰振风洞模拟试验系统。图4（a）中显示了置于风洞内的覆冰四分裂导线模型与水平吊架连接，通过与水平吊架连接的竖直弹簧和水平弹簧悬挂在刚性支架上。各竖直弹簧的刚度为40N／m，各水平弹簧的刚度为36N／m。此外，在吊架上安装三个LED点光源，与每个点光源对应安装一个CCD摄像机，以记录试验过程中导线的运动轨迹。图4（b）中CCD摄像机与数据采集系统连接，计算机采集记录三个光点的运动轨迹，从而可得到覆冰导线的垂直、水平位移时程及其运动轨迹。

2.3 试验结果

分别对新月形和扇形两种形状的覆冰四分裂导线节段模型进行了驰振模拟试验。现分别给出两种冰形情况下的试验结果。

对于新月形覆冰四分裂导线节段模型，由作者试验得到的28mm厚新月形覆冰导线空气动力学系数随风迎角变化曲线［9］可知，当风迎角在40°～100°范围内其升力系数曲线斜率为负，根据Den Hartog舞动机理，风迎角在此范围内可能诱发垂直舞动，故选取初始迎角60°进行试验。此外，当覆冰导线的扭转固有频率与垂直频率接近时，更容易诱发驰振，故试验时通过调节弹簧刚度和配重等改变系统的固有频率使该两频率接近。调整后测得系统竖直方向的1阶固有频率为0.69Hz，扭转方向的固有频率为0.75Hz，两者之比为0.92。

图4 覆冰导线节段模型驰振风洞模拟试验系统Fig.4 Wind－tunnel test system for galloping of iced quad bundle conductor

图5 新月形覆冰四分裂导线节段模型驰振试验结果（U＝9m／s，θ0＝60°）Fig.5 Galloping test results of quad bundle conductor with crescent－shaped ice

图5所示为风速为9m／s时新月形覆冰四分裂导线节段模型驰振风洞模拟试验结果，图中给出了导线的垂直和水平位移时程曲线以及驰振运动轨迹。可见，导线模型的驰振主要为垂直运动，运动轨迹近似为椭圆，和实际观测的Den Hartog垂直舞动现象相符。

对于扇形覆冰四分裂导线节段模型，由18mm厚扇形覆冰导线空气动力学系数随风迎角变化曲线［9］可知，当风迎角在130°附近时其升力系数曲线斜率为负，可能诱发Den Hartog垂直舞动，故选取初始迎角130°进行试验。调整后测得系统竖直方向的1阶固有频率为0.69Hz，扭转方向的固有频率为0.70Hz，两者之比近似为1。

图6所示为风速为8m／s时扇形覆冰四分裂导线节段模型驰振风洞模拟试验结果，图中给出了导线的垂直和水平位移时程曲线以及驰振运动轨迹。与

3 导线节段模型驰振试验的有限元模拟

图6 扇形覆冰四分裂导线节段模型驰振试验结果（U＝8m／s，θ0＝130°）Fig.6 Galloping test results of quad bundle conductor with sector－shaped ice

新月形覆冰情况类似，运动轨迹仍然近似为椭圆，类似于实际输电线路的垂直舞动现象。

3.1 有限元模型

本文作者提出了一种求解覆冰分裂导线舞动的数值模拟方法［5］，在此利用该方法模拟两个覆冰导线节段模型风洞试验的驰振过程，进而对该数值方法进行验证。

将覆冰四分裂导线风洞试验模型简化为如图7所示的数值模型。在数值模型中，用具有扭转自由度的索单元模拟覆冰导线，用空间梁单元模拟水平吊架。固定四根分裂导线的两个圆盘简化为图中所示的梁结构，两根梁的质量与一个圆盘的质量相等。此外，系统中的弹簧用弹簧单元模拟。

图7 覆冰四分裂导线节段试验有限元模型Fig.7 Finite element model of iced quad bundle conductor test model

本文作者利用风洞试验测量了不同厚度新月形和扇形覆冰四分裂导线在不同风速下的升力系数、阻力系数和扭矩系数随风迎角的变化规律［9］，这些系数曲线可用于计算节段模型驰振过程中的气动载荷。气动荷载的计算和驰振的数值模拟方法详见文献［5］。

3.2 数值模拟结果及其与风洞试验的比较

数值模拟得到的新月形覆冰导线节段模型的驰振结果如图8所示，图中给出了垂直位移和水平位移时程和驰振轨迹。比较图8和图5的结果可见，数值模拟得到的垂直位移与试验较接近，而水平位移数值模拟结果与试验结果偏差相对较大。出现较大偏差的原因，一方面可能与气动参数风洞试验结果的误差有关；另一方面，数值模型可能与真实试验系统之间存在差异。但总的来讲，数值模拟结果与试验结果表现出较好的一致性。

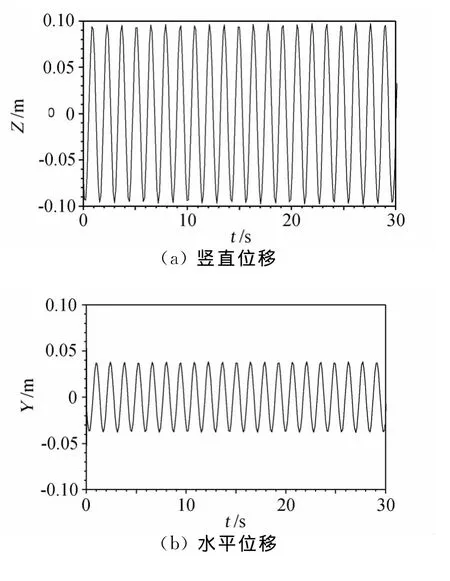
图8 新月形覆冰四分裂导线节段模型驰振数值模拟结果（U＝9m／s，θ0＝60°）Fig.8 Numerical galloping results of quad bundle conductor with crescent－shaped ice

图9 扇形覆冰四分裂导线节段模型驰振数值模拟结果（U＝8m／s，θ0＝130°）Fig.9 Numerical galloping results of quad bundle conductor with sector－shaped ice

数值模拟得到的扇形覆冰导线节段模型的驰振结果如图9所示。比较图9和图6的结果可见，数值模拟得到的垂直位移、水平位移和运动轨迹均与试验结果吻合。由两个模型的数值模和试验结果的一致性，验证了本文作者提出的覆冰分裂导线舞动数值方法的正确性。

4 结 论

本文设计制作了覆冰四分裂导线节段模型驰振模拟风洞试验系统，测试了典型厚度新月形覆冰和扇形覆冰四分裂导线节段模型在典型风速下的驰振过程，给出了导线垂直位移和水平位移时程曲线和运动轨迹。利用获得的覆冰分裂导线舞动数值模拟方法模拟节段模型的驰振过程，得到一致的结果，验证了数值方法的正确性。风洞试验方案合理，试验数据可靠，对覆冰导线舞动研究具有重要的参考价值。

［1］GUO Y L，LI G X，YOU C Y，Galloping of transmission lines［M］.Beijing：China Electric Power Press，2003.1（in Chinese）郭应龙，李国兴，尤传永，输电线路舞动［M］，北京：中国电力出版社，2003.1.

［2］LUONGO A，PICCARDO G.Linear instability mechanisms for coupled translational galloping［J］.Journal of Sound and Vibration，2005，288：1027－1047.

［3］DESAL Y M，YU P，POPPLEWEL N，SHAH A H，Finite element modeling of transmission line galloping［J］.Computers ＆ Structures，1995，57（3）：407－420.

［4］ZHANG Q，POPPLEWEL N，SHAH A H，Galloping of bundled conductor［J］.Journal of Sound ＆ Vibration，2000，234（1）：115－134.

［5］LIU X H，YAN B，ZHANG H Y，et al.Nonlinear finite element method for bundle conductors［J］.Journal of Vibration and Shock，2010，29（6）：129－133.（in Chinese）刘小会，严波，张宏雁，等.分裂导线舞动非线性有限元方法［J］.振动与冲击，2010，29（6）：129－133.

［6］HU J，YAN B，ZHOU S，ZHANG H Y.Numerical investigation on galloping of iced quad bundle conductors［J］.IEEE Transactions on Power Delivery，2012，27（2）：784－792.

［7］CHABART O，LILIEN J L.Galloping of electrical lines in wind tunnel facilities［J］.Journal of Wind Engineering and Industrial Aerodynamics，1998（74－76）：967－976.

［8］LI W P，YANG X X，ZHANG L Z，Static aerodynamic characteristics of the galloping of bundled iced power transmission lines［J］.ACTA Aerodynamica Sinica，1995，13（4）：427－433.（in Chinese）李万平，杨新祥，张立志.覆冰导线群的静气动力特性［J］.空气动力学学报，1995，13（4）：427－433.

［9 ］ZHANG H YYAN BZHOU Set al.Static test on aerodynamic characteristics of iced quad bundled conductors［J］.ACTA Aerodynamica Sinica，2011，29（2）：150－154.（in Chinese）张宏雁，严波，周松，等.覆冰四分裂导线静态气动力特性试验研究［J］.空气动力学报，2011，29（2）：23－27.

［10］MA W Y，GU M，QUAN Y，et al.Testing study on aerodynamic force characteristics of quasi－oval shape iced conductor［J］.Journal of Tongji University（Natural Science），2010，38（10）：1409－1413.（in Chinese）马文勇，顾明，全涌，等.准椭圆形覆冰导线气动力特性试验研究［J］.同济大学学报，2010，38（10）：1409－1413.

［11］GURUNG C B，YAMAGUCHI H，YUKINO T，Iden－tification of large amplitude wind－induced vibration of ice－accreted transmission lines based on field observed data［J］.Engineering Structures，2002，24：179－188.

［12］DYKE P V，LANEVILLE A，Galloping of a single conductor covered with a D－section on a high－voltage overhead test lines［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96：1141－1151.

［13］LOREDO－SOUZA A M，DAVENPORT A G，A novel approach for wind tunnel modelling of transmission lines［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89：1017－1029.

［14］LOREDO－SOUZA A M，DAVENPORT A G，Wind tunnel aeroelastic studies on the behaviour of two parallel cables［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90：407－414.