谱单元法及其在多圆柱绕流分析中的应用

韩兆龙，周 岱，陈亚楠，桂晓澜，李俊龙

（上海交通大学 船舶海洋与建筑工程学院，上海 200240）

谱单元法及其在多圆柱绕流分析中的应用

韩兆龙，周 岱，陈亚楠，桂晓澜，李俊龙

（上海交通大学 船舶海洋与建筑工程学院，上海 200240）

系统阐明谱单元方法，基于谱单元方法对低雷诺数Re＝200时不同间距下的顺排两圆柱和Re＝150正方形排列的四圆柱绕流及其阻力系数、升力系数等进行数值模拟。研究比较不同间距比L／D（两圆柱圆心距离与圆柱直径之比）对两圆柱和四圆柱绕流的影响，计算分析了涡量图分布、平均阻力系数和斯托罗哈数随间距比的变化。研究表明，间距比对顺排两圆柱和正方形四圆柱绕流影响显著；顺排两圆柱绕流存在临界间距比，在Re＝200时临界间距比约为3．6。正方形排列四圆柱存在三种流态。当流场从一种流动形态变成另外一种流动形态时，力学参数发生显著变化，在某些间距比区间内出现骤升或骤降现象。

谱单元法；顺排两圆柱；正方形四圆柱；间距比；流动形态

0 引 言

自从1977年Gottlieb和Orszag［1］系统性地从数学方面对谱方法进行了理论阐述以来，谱方法被广泛地应用于更多的领域。1984年，Gottlieb和Hussaini开始将谱方法向计算流体动力学推广［2］。20世纪80年代初期，Patera结合谱方法的精度和有限元的思想提出了所谓的谱单元法［3］。谱单元法是谱方法与有限元方法结合起来，将求解区域剖分成单元，采用等参元，在每个单元内用N阶多项式展开来近似变量，对方程采用Galerkin方法，用Gauss点求积分，得到离散化的方程组。当单元数目固定时，计算精度随多项式阶数N的增加而增加。因此，谱单元法是求解偏微分方程的一种高阶加权余量法，它继承了有限元方法对复杂几何区域的适应性和谱方法的高精度与收敛特性等优点。

圆柱绕流的理论研究和工程应用意义重大。顺排两圆柱或多圆柱是常见的排列形式，例如发电厂冷却塔群等。圆柱尾流中的旋涡脱落对圆柱绕流的周期性升力、阻力产生影响，引起压力脉动、切应力脉动和升阻力系数的脉动。相对于单圆柱的绕流，两圆柱或多圆柱绕流及其流致受力更为复杂。现今，有限体积法、Boltzmann等多种数值模拟方法可用于分析圆柱绕流，获取柱体表面上的作用力和关键参数［4-6］。

本文较系统阐述谱单元方法及其表达，运用谱单元方法数值模拟低雷诺数Re＝200下的顺排两圆柱、Re＝150正方形排列四圆柱的绕流及其互扰效应，分析不同间距比对流场特性的影响，揭示平均升阻力系数和斯托罗哈数（旋涡脱落频率）等随间距比的变化，并解释其形成机制。

本文的数值计算采用由Monash大学的Blackburn教授所提供的Semtex程序，对二维计算，该程序采用Gauss-Lobatto-Legendre（GLL）多项式作为谱单元基函数，时间和空间的数值精度可由使用人员自由控制。该方法已成功应用于多项科学研究［7-10］。

1 基本理论和计算公式

二维粘性不可压缩非定常流动的控制方程为Navier-Stokes方程：

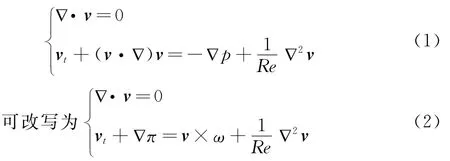
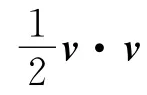
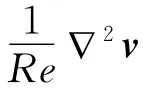
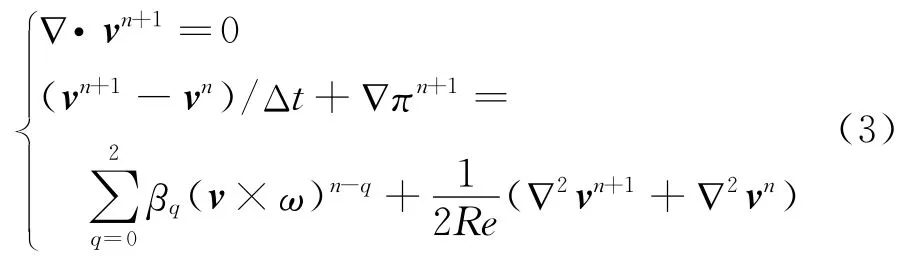
采用基于混合刚性稳定格式的高阶时间分裂算法［7］，可将Navier-Stokes方程的求解转化为如下三部分：

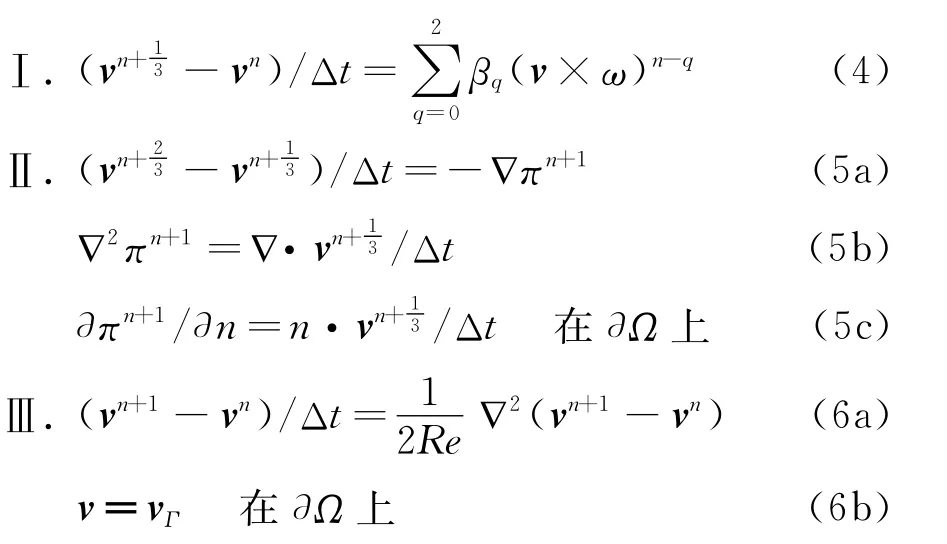
流体压力满足泊松方程：

对流体域的空间离散，采用谱单元法，且选取Legendre多项式［7］的极值点作为插值点。

Φ（Ω）（Ω上任意连续函数构成的空间）中的任何连续实函数u（x）可表示为：

插值多项式

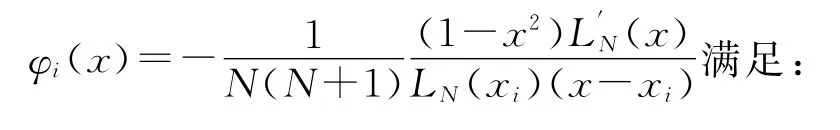
（1）在［-1，1］以外为0；（2）在［-1，1］内，φi（xj）＝δij。其中LN（x）为Legendre多项式。

若将式（4）、（5a）、（5b）、（6a）写成变分形式，则有：

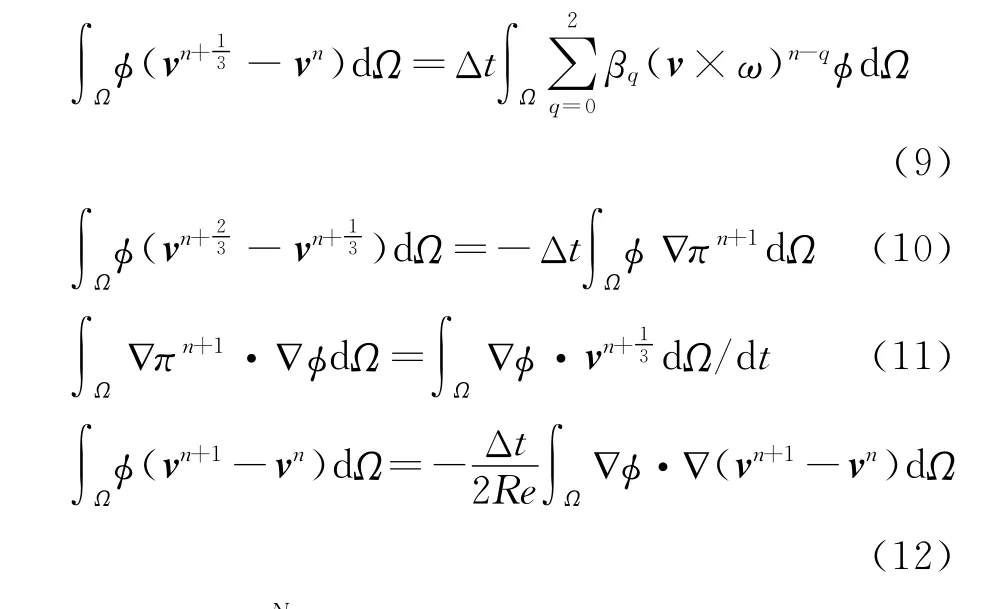
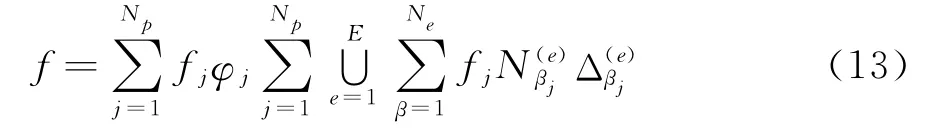
对计算区域Ω采取等参变换，且取φ＝φj，Navier-Stokes方程的离散格式变为：

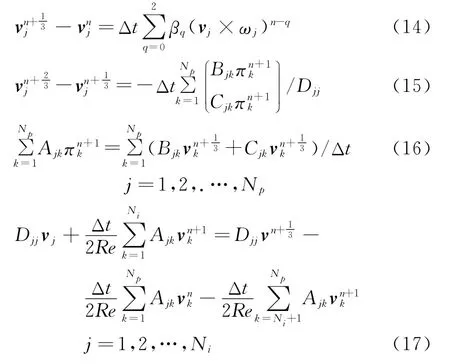
其中

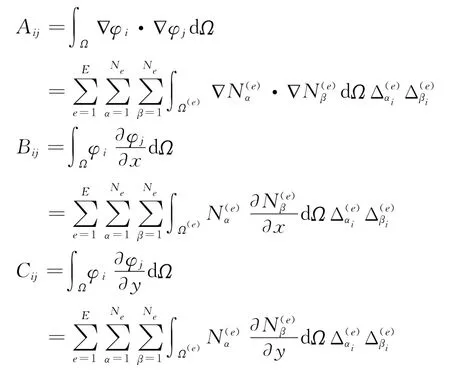
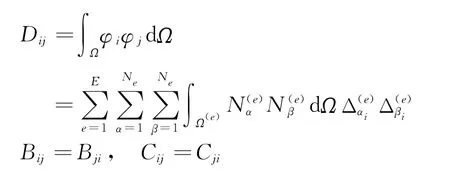
选取Legendre多项式，并利用Gauss积分，各系数计算公式为

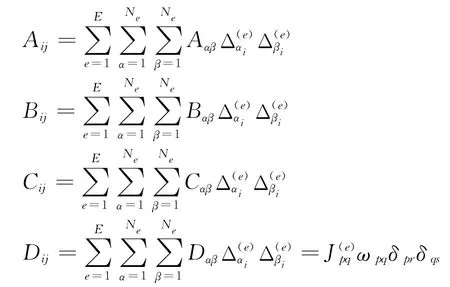
其中

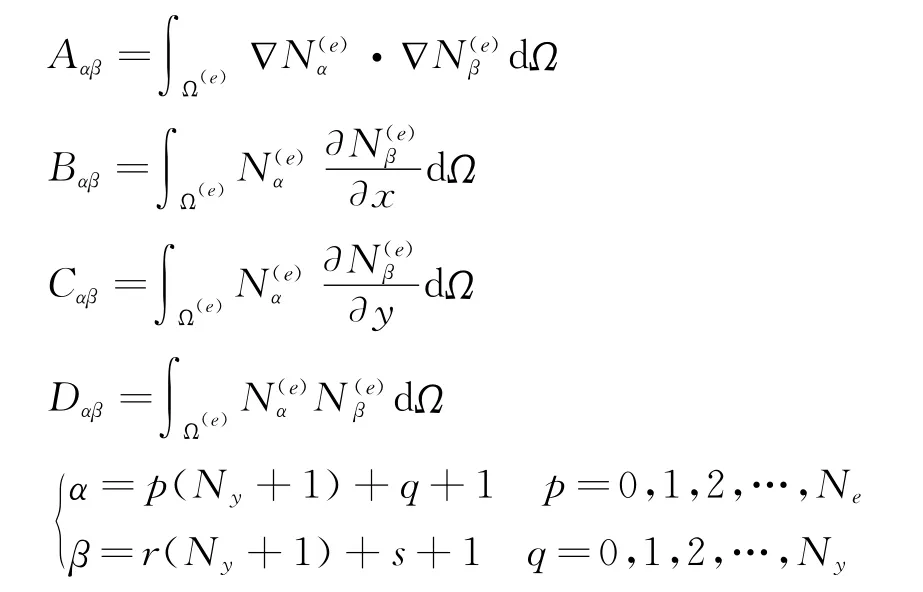
其中，［φb］表示相应变量（压力或速度）在计算区域边界点上的未知值，［φi］表示相应变量是在计算区域的内点上的未知值。

先由下式解出边界上的未知物理量值：

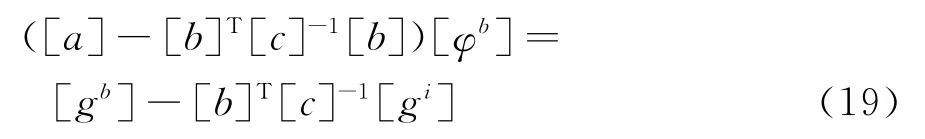
再由下式解出计算区域内点的未知物理量值：

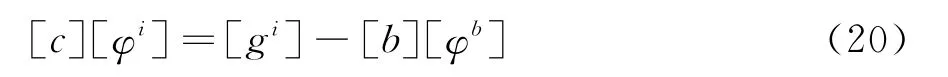
若求解的方程组维数较高，可采用对单元（而不是对计算区域）求解的策略，即先采用类似于式（19）的方程求得各个单元边界上的未知量值，而后再对各个单元分别求解其内点上的未知物理量值。

2 单圆柱绕流模拟与数值验证

为验证计算的准确性和可靠性，兹选用图1示的单圆柱绕流问题进行数值方法验证。考虑直径为D的圆柱受未经扰动的均匀来流作用，基于圆柱直径和来流流速的雷诺数取Re＝200。选定计算域为50D×40D，圆柱位于坐标系原点（0，0）。入口边界和出口边界分别位于圆柱中心上游20D和下游30D处，流域顶部和底部离圆柱中心20D。相应的边界条件为：进口处自由来流速度为特征速度，即u＝U∞＝1，v＝0．0；上下边界条件与进口边界条件相同；出口边界处压力均为0．0，即p＝0．0；圆柱表面处为不可滑移边界条件，即u＝0．0，v＝0．0。计算域网格划分采用四边形非结构化谱单元网格，网格单元数为354，如图1（a）所示。在靠近圆柱壁面的地方进行几层细化网格加密，离圆柱壁面最近的一层网格厚度为0．1D，如图1（b）示。同时，在圆柱尾流区域亦进行加密处理。

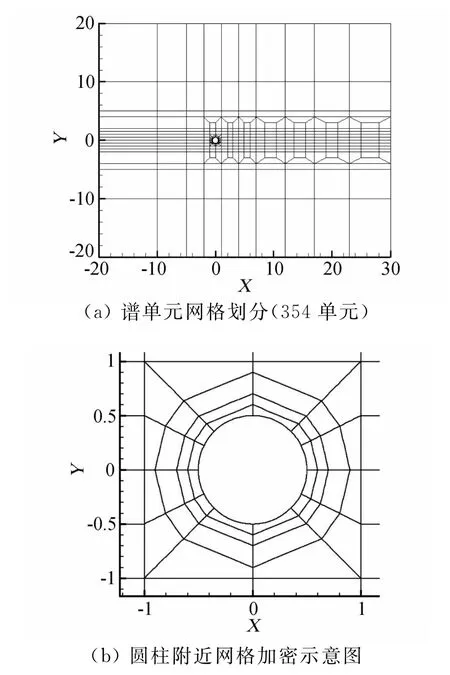
图1 单圆柱绕流的谱单元网格示意Fig.1 Mesh system of spectral element for cross-flow around a single cylinder

研究圆柱绕流流场常用的无量纲化系数包括阻力系数CD、升力系数CL和斯托罗哈数St，定义为：

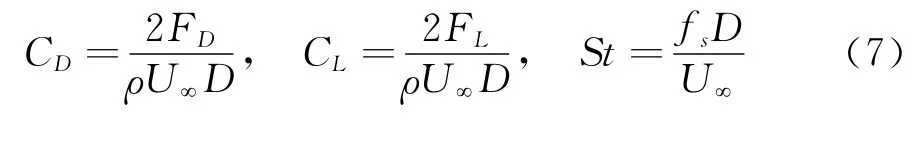
其中，FD为阻力，与来流方向一致，主要由流体圆柱前后压力差和绕圆柱柱表面摩擦阻力造成；FL为升力，与来流方向垂直，主要由涡交替从圆柱上下表面脱落产生上下表面压力脉动造成；fs为旋涡脱落频率，D为圆柱直径。

为分析插值函数的阶数对计算结果的影响，对单圆柱绕流的三种计算工况进行基于三种不同阶数的插值函数的数值模拟。计算工况1中，谱函数插值采用N＝5阶Gauss-Lobatto-Legendre多项式形函数；计算工况2中，N＝7；工况3中，N＝9。计算时间步长Δi＝0．005。从表1中看出，采取高阶谱插值的谱单元法的计算精度和效率较高，即使对较粗糙网格划分，当N＝5、7、9时，亦可得到满意的结果，且与既有文献中的实验结果和数值模拟结果吻合。为取得计算精度和计算效率的平衡，本文取N＝7。这样，计算的空间精度为7阶，时间上的精度为2阶。

需要说明的是，尽管在本单圆柱扰流的算例中Re＝200有弱三维效应，但是本研究采用二维计算，仍能得到与其他文献接近的结果。

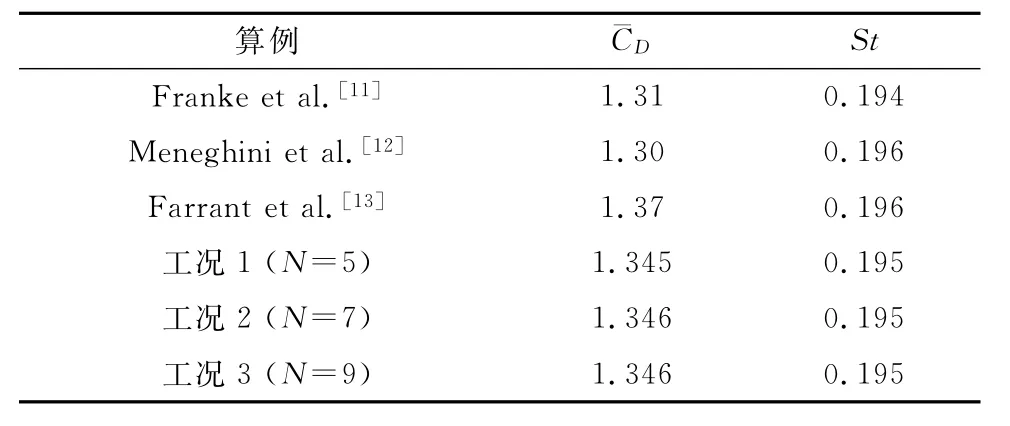
表1 平均阻力系数和斯托罗哈数（雷诺数Re＝200）Table 1 Average drag coefficients and Strouhal numbers（Re＝200）

3 顺排两圆柱绕流数值模拟

将两圆柱顺排排列放置在流体中，通过改变圆柱轴线之间的距离L，分析流场的变化。取Re＝200，计算时间步长Δi＝0．005，采用N＝7阶插值函数，数值模拟间距比L／D＝1．2、1．5、2．0、3．6、4．0、6．0、8．0和10．0情形下的流场。

3.1 计算域和边界条件

流场计算域和边界条件与上述单个圆柱绕流数值模拟情形相同，图2为计算域和边界条件示意图。图3（a）为两圆柱圆心间距为2．5D时的网格划分示意图，共划分432个网格，在靠近圆柱壁面的几层进行细化网格加密处理，离圆柱壁面最近的一层网格厚度为0．1D，如图3（b）所示。同时，在圆柱尾流区域进行加密处理。

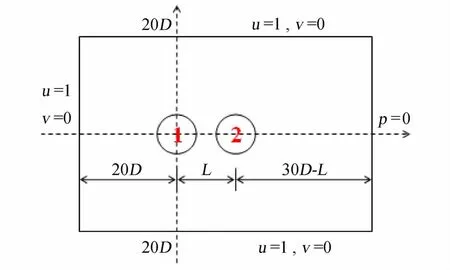
图2 双圆柱顺排排列的计算域和边界条件示意图Fig.2 Schematic diagram of the computational domain and boundary conditions

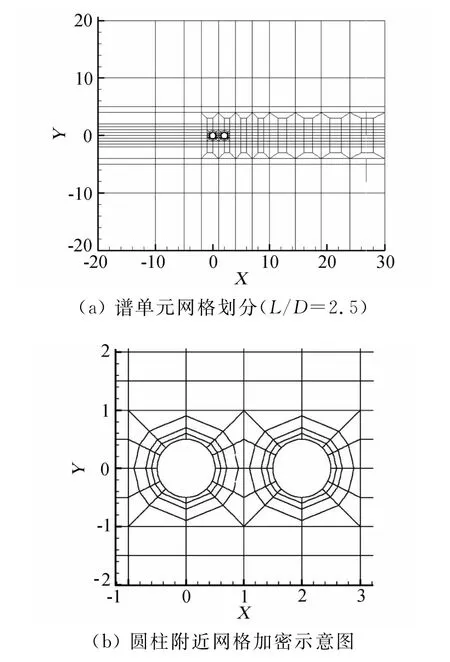
图3 两圆柱绕流的谱单元网格示意图Fig.3 Mesh system of spectral element for cross-flow around two cylinders

3.2 不同间距比下的流态

图4为不同间距比下的顺排两圆柱绕流涡量图，从图4中看出，当两圆柱串列时存在一个临界间距，小于临界间距时，上游圆柱后不存在旋涡脱落；大于临界间距时，上游圆柱后发生周期性旋涡脱落。据图4可定性判定出此临界间距比大约为L／D≈3．6；即当L／D＜3．6时，上游圆柱后没有产生涡脱落，上游圆柱绕流的分离分界层附着在下游圆柱上，而下游圆柱的后侧产生涡脱落，尾流模式类似于单圆柱绕流尾流模式，当L／D＝3．6时，上游圆柱后开始形成涡脱落，当L／D＝4时，上游圆柱的后侧已形成Kármán涡街，且旋涡脱落后撞击下游圆柱前表面，干扰下圆柱的旋涡脱落模式，随着间距比的继续增大，上游圆柱后的脱落涡继续影响下游圆柱的尾流。Re＝200时，圆柱绕流发生三维效应；可以看到上游圆柱后的涡脱落稳定，但下游圆柱后的尾流涡脱落形态变得复杂，因此二维数值模拟不能精确确定临界间距比周围的互扰区域。

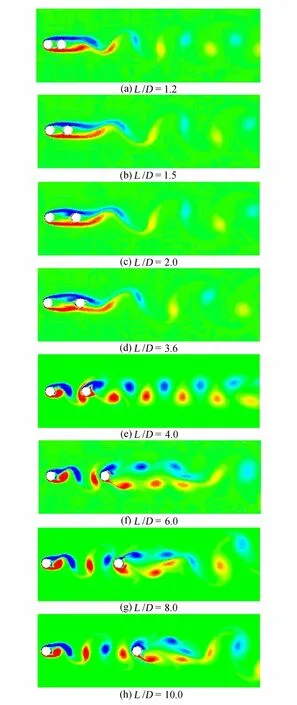
图4 双圆柱不同间距比下的涡量云图Fig.4 Vorticity contours with different spacing ratios for the two cylinders

3.3 圆柱表面受力特性随间距比的变化

图5为两圆柱绕流平均阻力系数随间距比的变化。从图5可以看到，两圆柱的平均阻力系数均小于单个圆柱的平均阻力系数，圆柱1（上游圆柱）的平均阻力系数要大于圆柱2（下游圆柱）的平均阻力系数。对于小间距比下圆柱1，先观察到其平均阻力系数随着间距比的增大而减小，间距比L／D＝3．6的时取得最小值；然后随着间距比增大，平均阻尼增大，在L／D＝3．6和L／D＝4之间剧增后，其值缓慢增大，逐渐接近于单个圆柱的平均阻力系数。对于圆柱2，间距比L／D＜3．6时，其值随着间距比增大而增大，在L／D＝3．6和L／D＝4之间剧增，从负值变到相当大的正值，之后又缓慢减小，趋于稳定。从中易见临界间距比的存在（3．6＜L／D＜4．0）。当间距比小于临界值时，上游圆柱的分离剪切层附着在下游圆柱上，涡脱落现象只在下游圆柱出现，此时下游圆柱受到较小的阻力，且为负值。当间距比大于临界值时，上下游圆柱均产生涡脱落，且升力振幅均骤然增大（图4g），平均阻力系数突然变大，下游圆柱变化更剧烈。之后，随着间距比继续增大，上下游圆柱的涡脱落均呈现出稳定性，变化缓慢。

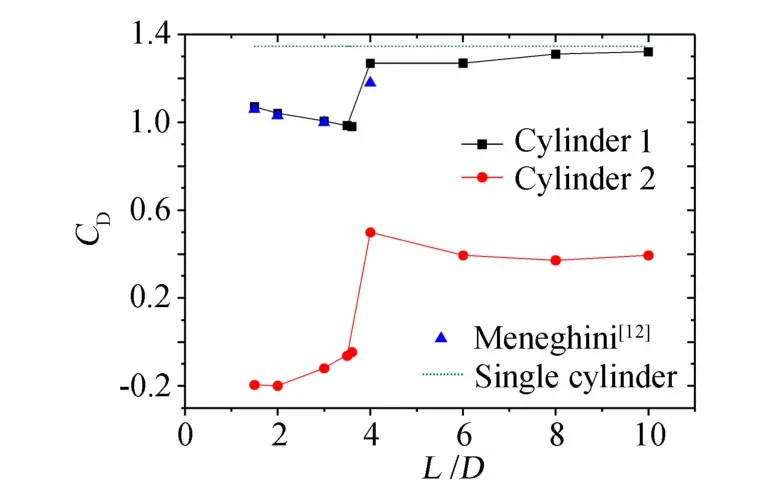
图5 双圆柱平均阻力系数随间距比的变化Fig.5 Variation of mean drag coefficients with different spacing ratios for the two cylinders

3.4 斯托罗哈数随间距比的变化

本文所有变量均经过无量纲化处理，因此斯托罗哈数即等于涡脱落频率。涡脱落频率可通过对升力曲线作FFT分析求得。

图6为斯托罗哈数随间距比的变化。总体上，两圆柱的斯托罗哈数基本保持相等，均随着间距比的增大先减小再增大，并趋向于单个圆柱绕流时的斯托罗哈数。但间距比在某些区间内对斯托罗哈数的影响显著，即间距比从3．6增大到4．0时，斯托罗哈数剧烈增大。当间距比小于临界值时，上游圆柱后无涡脱落，仅下游圆柱后产生涡脱落；当间距比大于临界值时，上游圆柱和下游圆柱均存在周期性的涡脱落，从而使得斯托罗哈数在临界间距之间发生显著跳跃。同样，在双圆柱扰流的算例中Re＝200有弱三维效应，二维计算，仍能得到与其他文献较好拟合的结果。

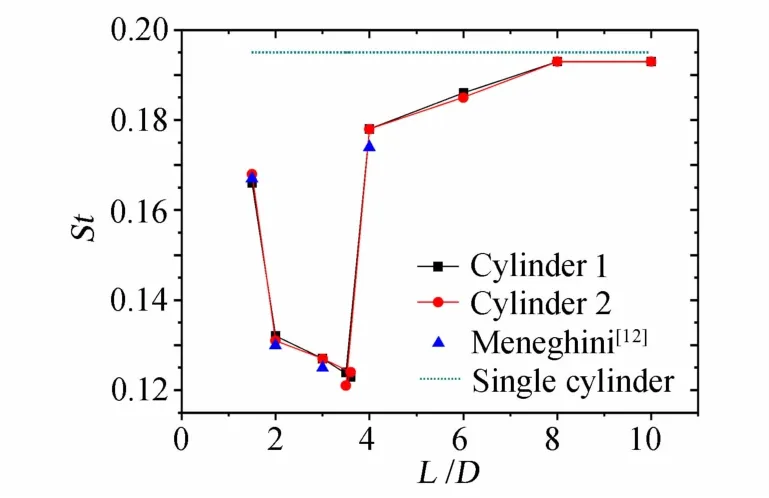
图6 斯托罗哈数随间距比的变化Fig.6 Variation of the Strouhal numbers，St，with different spacing ratios，L／D for the two tandem cylinders

4 正方形顺排排列四圆柱绕流数值模拟

把四圆柱绕正方形顺排排列放置在流体中，通过改变圆柱轴线之间的距离L，分析流场的变化。取Re＝150，计算时间步长Δi＝0．005，采用N＝7阶插值函数，数值模拟L＝1．4D、2．5D、3．5D和4．0D时的流场。在Re＝150这样的雷诺数下，流体无三维效应。同样，计算的空间精度为7阶，时间上的精度为2阶。

4.1 计算域和边界条件

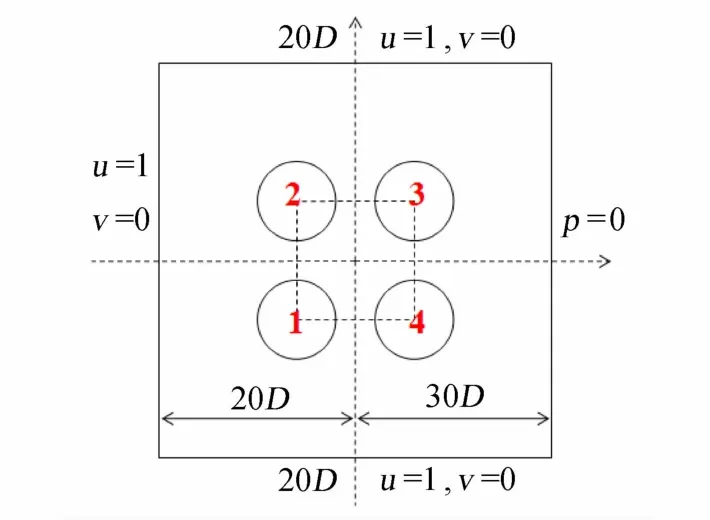
图7 四圆柱排列的计算域和边界条件示意图Fig.7 Schematic diagram of the computational domain and boundary conditions for four cylinders

流场计算域和边界条件与上述单圆柱绕流数值模拟情形相同，图7为计算域和边界条件示意图。图8（a）为两圆柱圆心间距为2．5D时的网格划分示意图，共划分778个网格，在靠近圆柱壁面的地方进行几层网格加密，离圆柱壁面最近的一层网格厚度为0．1D，如图8（b）所示。同时，在圆柱尾流区域进行加密处理。

图8 四圆柱绕流的谱单元网格示意图Fig.8 Mesh system of spectral element for cross-flow around four cylinders

4.2 不同间距比下的流态

图9为不同间距比下的四圆柱绕流的涡量云图。观察发现三种不同的流动形态：间距比较小（L／D＝1．4）时，圆柱互扰以临近效应为主，上游两个圆柱后面靠内侧的自由剪切层附着在下游两个圆柱表面，但是靠外侧的两个自由剪切层并未附着在下游两个圆柱表面，而是覆盖下游两个圆柱，并从下游两个圆柱后面流出，内外两侧的自由剪切层未出现摆动，圆柱尾流呈现为单钝体绕流流动形态；在中等间距比（L／D＝2．5）条件下，结构互扰以临近效应和剪切层干扰为主，上游两个圆柱后面靠内侧的自由剪切层再附着在下游两个圆柱表面，但是靠外侧的两个自由剪切层并未再附着在下游两个圆柱表面，而是在下游两个圆柱表面交替出现摆动，此时下游圆柱尾部形成旋涡脱落流态，且干扰上游圆柱尾部旋涡发展并抵制其脱落；圆柱间距比较大（L／D＝3．5／4．0）时，结构互扰以尾流效应为主，此时所有圆柱尾流均充分发展，上游圆柱的自由剪切层形成成熟的涡脱落，然后撞击到下游圆柱，且剪切层不断向下游泄送Kármán旋涡，圆柱互扰表现为相邻剪切层之间的相互干扰。由上可见，流动形态明显影响圆柱表面的压力分布，尤其是当从一种流动形态转变到另一种流动形态，压力分布变化显著。

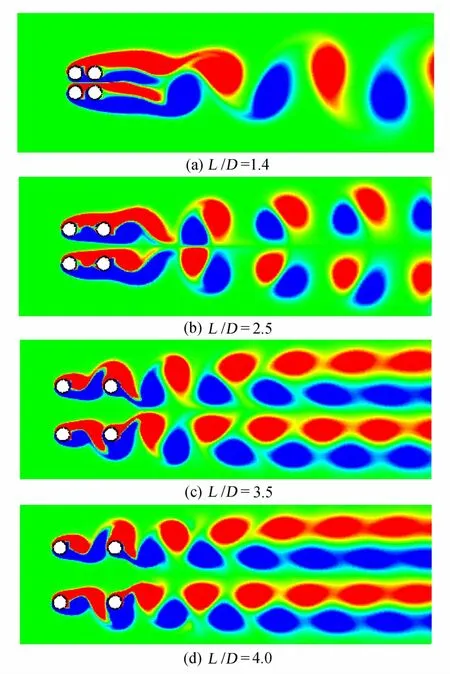
图9 不同间距比下的涡量云图Fig.9 Vorticity contours with different spacing ratios for the four cylinders

4.3 圆柱表面受力特性随间距比的变化

图10为四圆柱绕流情形下的柱体平均阻力系数随间距比的变化，同时与相关文献［11-12］在不同雷诺数下的结果对比。从图10中看出，圆柱1和2的平均阻力系数CD1和CD2基本上相等，圆柱3和4CD3和CD4也呈现相同的特征，这是对称性造成的结果，但是在间距比较小时，则有细微差异。另外，比较不同雷诺数的结果，发现雷诺数对阻力系数的影响较大，但是数值在同一数量级范围内。

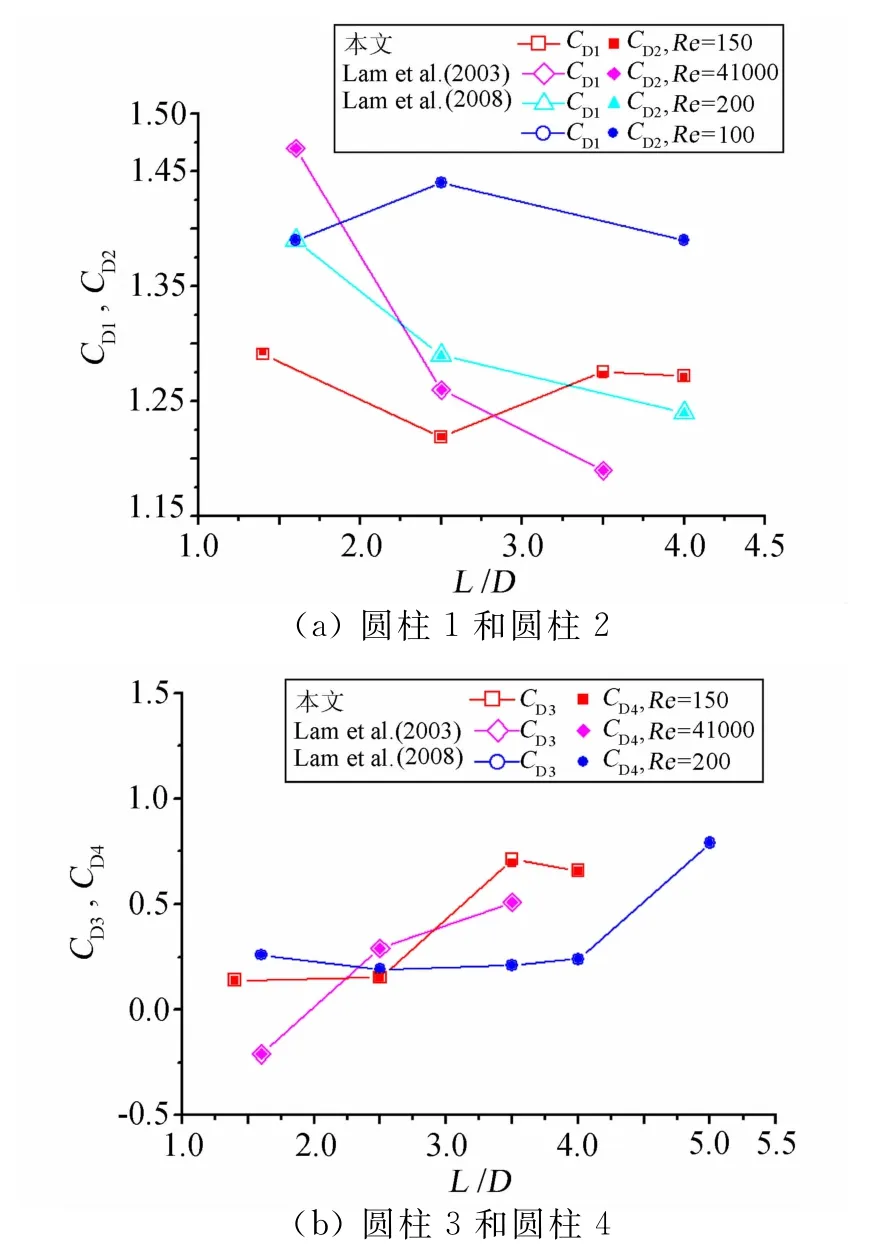
图10 四圆柱平均阻力系数随间距比的变化Fig.10 Variation of mean drag coefficients with different spacing ratios for the four cylinders

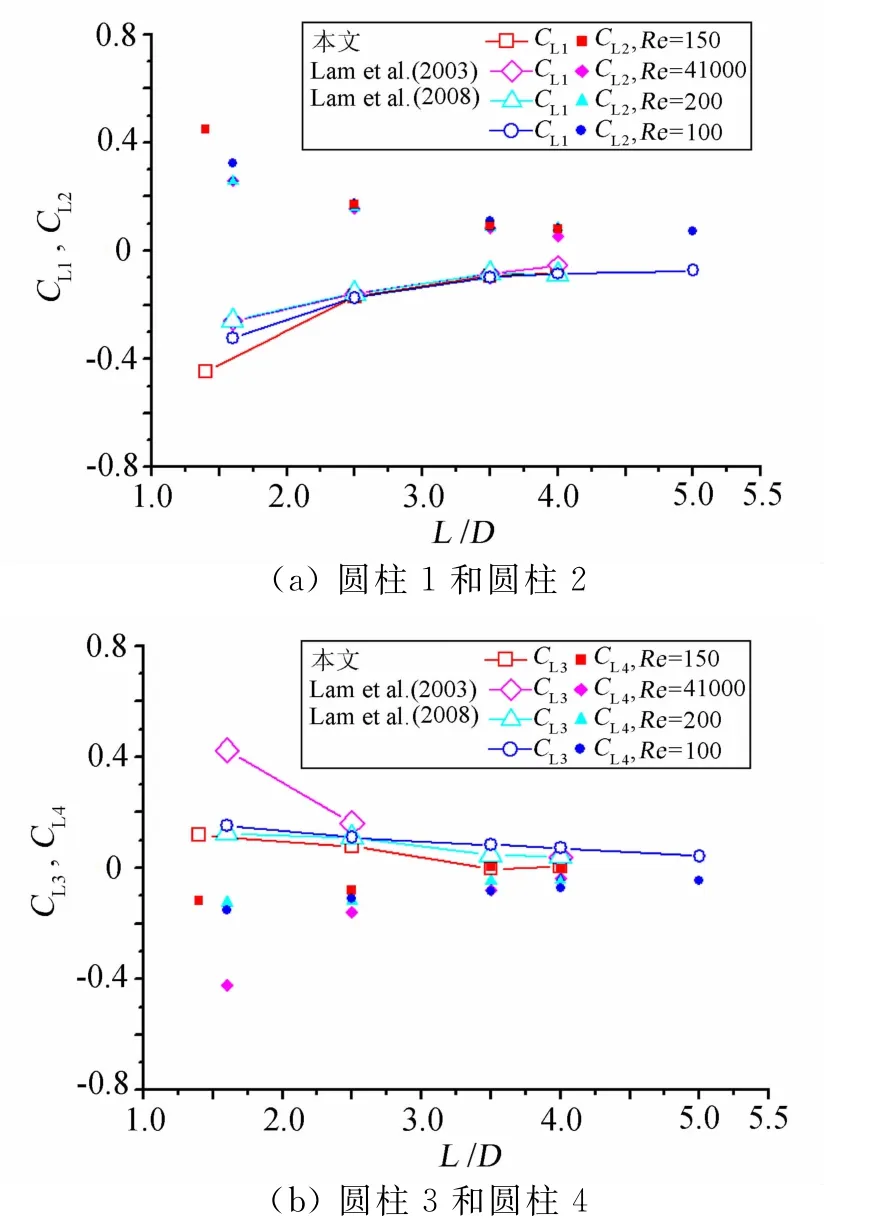
图11 四圆柱平均升力系数随间距比的变化Fig.11 Variation of mean lift coefficients with different spacing ratios for the four cylinders

图11为四圆柱绕流情形下的柱体平均升力系数随间距比的变化，同时与相关文献［14-15］在不同雷诺数下的结果对比。从图中可见，圆柱1和2平均升力系数CL1和CL2相反，圆柱3和4平均升力系数CL3和CL4也相反，这反映出两对圆柱间互相排斥。随着间距比的增大，4个圆柱的平均升力系数的绝对值均减小，且趋于0。上游两个圆柱的平均升力系数绝对值大于下游两个圆柱。在层流范围内不同雷诺数的情况下，柱体的平均升力系数接近。但是在湍流情况下，间距越小，平均升力系数会更大。

4.4 斯托罗哈数随间距比的变化

图12为四圆柱绕流情形下的斯托罗哈数St1-St4随间距比的变化。因本文变量均经无量纲化处理，所以斯托罗哈数即等于旋涡脱落频率。旋涡脱落频率可通过对升力曲线作傅立叶变换（FFT）分析求得。从图9中看出，四个圆柱旋涡脱落频率近乎相同。从L／D＝1．4到L／D＝2．5是从一种尾流形态转变成另一种完全不同尾流形态，旋涡脱落频率有所减小，从L／D＝2．5到L／D＝3．5尾流形态再发生转变，旋涡脱落频率增大。L／D＝1．4时，尾流形态类似于单钝体绕流时的尾流，尾流只有一个占主要地位的旋涡脱落；L／D＝2．5时，上下侧两对圆柱尾流中分别形成旋涡脱落，类似于两对反对称的串列圆柱，但是每一对串列圆柱后面的尾流又不同于两串列圆柱时的尾流，尾流中有一个占主要地位的旋涡，还有一个小涡伴随，而并非两排相同大小的旋涡；之后随着间距比继续增大，旋涡脱落频率随之增大，并逐渐趋近于单圆柱绕流时的旋涡脱落频率，上下两侧尾流形态也类似于两对串列圆柱尾流形态。

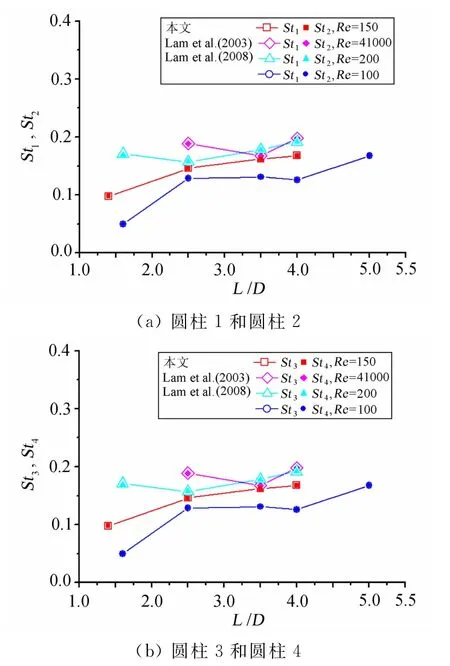
图12 四圆柱斯托罗哈数随间距比的变化Fig.12 Variation of the Strouhal numbers with different spacing ratios for the four cylinders

比较雷诺数的影响，发现从层流到湍流范围内，旋涡脱落频率在0．05～0．2之间，在同一数量级。

5 结 论

本文系统阐明了谱单元方法的基本原理，基于谱单元方法对低雷诺数和不同间距比下的顺排双圆柱绕流和正方形排列的四圆柱扰流及其阻力系数、升力系数等关键参数进行数值模拟和比较分析。

对顺排双圆柱扰流Re＝200，间距比选择包括1．2、1．5、2．0、3．6、4．0、6．0、8．0和10．0等八种。分析显示，间距比对两圆柱绕流流场特性影响明显，当流场从一种流动形态变成另外一种流动形态时，关键力学参数变化显著，在某些间距比区间内出现骤升或骤降的现象。顺排双圆柱绕流存在临界间距比，在Re＝200时临界间距比约为3．6；当间距比较小时（L／D≤3．6），上游圆柱后不发生涡脱落，而仅在下游圆柱后发生涡脱落；间距比增大时（L／D≥4．0），两圆柱之间产生涡脱落，且上游圆柱后的涡脱落对下游圆柱产生较大的影响。在临界间距比区间（3．6≤L／D≤4．0），平均阻力系数、平均阻力系数均方根、升力系数均方根和斯托罗哈数变化显著。

对于正方形排列四圆柱绕流问题在Re＝150，发现了三种不同的流动形态：间距比较小（L／D＝1．4）时，圆柱互扰以临近效应为主，圆柱尾流呈现为单钝体绕流流动形态；中等间距比（L／D＝2．5）时，结构互扰以临近效应和剪切层干扰为主，此时下游圆柱尾部形成旋涡脱落流态，且干扰上游圆柱尾部旋涡发展并抑制其脱落；圆柱间距较大（L／D＝3．5／4．0）时，结构互扰以尾流效应为主，此时所有圆柱尾流均充分发展，且剪切层不断向下游泄送Kármán旋涡，圆柱互扰表现为相邻剪切层之间的相互干扰。圆柱1和圆柱2的平均阻力系数在L／D＝2．5处发生跳跃，四个圆柱的斯托罗哈数均在L／D＝2．5处有一个弯折，之后随着间距比的增大而增大。

［1］GOTTLIEB D，ORGSZAG S A．Numerical analysis of spectral method：theory and application［A］．CB Ms-NFS Monograph No 26．Society for Industry and Applied Mathematics［C］．Philadelphia，1977．

［2］GOTTLIEB D，HUSSAINI M Y，ORGSZAG S A．Theory and application of spectral method［A］．In：Voigt RG．Gottlieb D．Hussaini M Y．Spectral Method for Partial Differential Equation［C］．SIAM Philadelphia，1984：1-54．

［3］PATERA A T．A spectral element method for fluid dynamics：laminar flow in a channel expansion［J］．Journal of computattonal Phystcs，1984，154：468-488．

［4］TAN Lingyan．Numerical simulation of flow past a main cylinder with an affiliated cylinder［J］．Journal of Jtltn Untverstty（Sctence Edttton），2012，50（1）：69-72．（in Chinese）

谭玲燕．数值模拟放置附属圆柱的主圆柱绕流［J］．吉林大学学报（理学版），2012，50（1）：69-72．

［5］WANG Tong，CAO Shuyang，ZHOU Qiang．Investigation of aerodynamic lift of a circular cylinder in linear shear flows at subcritical Reynolds number［J］．Chtnese Quarterly of Mechantcs，2011，32（4）：473-479．（in Chinese）

王通，曹曙阳，周强．亚临界雷诺数线性剪切流场中圆柱的气动升力特性研究［J］．力学季刊，2011，32（4）：473-479．

［6］GONG Shuai，GUO Zhaoli．Lattice Boltzmann simulation of flow over a transversly oscillation circular cylinder［J］．Chtnese Journal of Theorettcal and Applted Mechantcs，2011，43（5）：809-818．（in Chinese）

龚帅，郭照立．横向振荡圆柱绕流的格子Boltzmann方法模拟［J］．力学学报，2011，43（5）：809-818．

［7］BLACKBURN H M，SHERWIN S J．Formulation of a Galerkin spectral element-Fourier method for three-dimensional incompressible flows in cylindrical geometries［J］．Journal of Computattonal Phystcs，2004，197：759-778．

［8］BLACKBURN H M，LOPEZ J M．Modulated waves in a periodically driven annular cavity［J］．Journal of Flutd Mechantcs，2011，667：336-357．

［9］BLACKBURN H M，SHEARD G J．On quasi-periodic and subharmonic Floquet wake instabilities［J］．Phystcs of Flutds，2010，22：031701-1-4．

［10］BLACKBURN H M，BARKLEY D，SHERWIN S J．Convective instability and transient growth in flow over a backward-facing step［J］．Journal of Flutd Mechantcs，2008，603：271-304．

［11］FRANKE R，RODI W，SCHONUNG B．Numerical calculation of laminar vortex shedding flow past cylinders［J］．Journal of Wtnd Engtneertng and Industrtal Aerodynamtcs，1990，35：237-257．

［12］MENEGHINI J R，SALTARA F，SIQUEIRA C L R，et al．Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements［J］．Journal of Flutds and Structures，2001，15：327-350．

［13］FARRANT T，TAN M，PRICE W G．A cell boundary element method applied to laminar vortex-shedding from arrays of cylinders in various arrangements［J］．Journal of Flutds and Structures，2000，14：375-402．

［14］LAM K，LI J Y，SO R M C．Force coefficient and strouhal numbers of four cylinders in cross flow［J］．Journal of Flutds and Structures，2003，18：305-324．

［15］LAM K，GONG W Q，SO R M C．Numerical simulation of cross-flow around four cylinders in an in-line square configuration［J］．Journal of Flutds and Structures，2008，24：34-57．

Numerical simulation of cross-flow around multiple circular cylinders by spectral element method

HAN Zhaolong，ZHOU Dai，CHEN Yanan，GUI Xiaolan，LI Junlong
（School of Naval architecture，Ocean and Civil Engineering，Shanghai Jiao Tong University，Shanghai 200240，China）

The details of the spectral element method are presented．Flow past two tandem circular cylinders at the Reynolds numberRe＝200 and four square-arranged circular cylinders with various spacing ratios atRe＝150 are numerically investigated．The effects of spacing ratiosL／D（ratio of center-to-center distance to diameter of cylinder）for the two cases above are main concerned．The relationship between the spacing ratio and the flow patterns，mean drag and lift coefficients as well as the Strouhal numbers are studied．The results reveal that the spacing ratio has a great impact on the flow characteristics of both the two-cylinder andthe four-cylinder cases．There is a critical spacing ratio of around 3．6 atRe＝200 for the case of two tandem cylinders．Three different flow patterns are observed in the case of four-cylinders．Among different flow patterns，a transformation from one pattern to another will change the drag／lift forces and vortex shedding frequencies．The key mechanical parameters jump suddenly in some critical spacing ratio intervals．

spectral element method；two tandem cylinders；four square-arranged cylinders；spacing ratio；flow patterns

O353.4

A doi:10.7638／kqdlxxb-2012.0070

0258-1825（2014）01-0021-10

2012-08-07；

2012-11-22

国家自然科学基金（51078230，11172174，51278297）、上海市优秀学术带头人计划（13XD1402100）项目资助

韩兆龙（1983-），男，工学博士，专业：结构工程，研究方向：风工程与流固耦合．E-mail：han．arkey＠gmail．com

周岱，男（1963-），工学博士，教授，研究方向：大跨空间结构与流固耦合．E-mail：zhoudai＠sjtu．edu．cn

韩兆龙，周 岱，陈亚楠，等．谱单元法及其在多圆柱绕流分析中的应用［J］．空气动力学学报，2014，32（1）：21-29．

10．7638／kqdlxxb-2012．0070．HAN Z L，ZHOU D，CHEN Y N，et al．Numerical simulation of cross-flow around multiple circular cylinders by spectral element method［J］．ACTA Aerodynamica Sinica，2014，32（1）：21-29．