机翼边界层的横流稳定性分析和转捩预测
黄章峰,逯学志,于高通
(1.天津大学力学系,天津 300072;2.空气动力学国家重点实验室,四川 绵阳 621000)
机翼边界层的横流稳定性分析和转捩预测
黄章峰1,2,逯学志1,于高通1
(1.天津大学力学系,天津 300072;2.空气动力学国家重点实验室,四川 绵阳 621000)
通过求解经典O-S方程(LST)、扩展的O-S方程(EOS)和线性抛物化稳定性方程(LPSE),对展向无限长、后掠角25°、迎角0°、来流Mach数0.8、单位Reynolds数6.79×106/m的机翼边界层进行了稳定性分析,结合eN方法进行了转捩预测。研究发现无限长后掠机翼在(x,ω)平面上的中性曲线没有下支,在(x,β)平面上的中性曲线呈反拇指的形状,横流不稳定性在机翼前缘占主导作用。当外界扰动进入边界层后,幅值将被直接放大,对于频率相同的扰动,首先是展向波数β大的增长起来,演化到一定位置开始衰减,然后是展向波数β小的逐渐增长起来,并且增长的指数N逐步超过波数大的扰动。转捩在机翼前缘完成,引起转捩的扰动波的展向波长约为2mm。
流动稳定性分析;转捩预测;横流不稳定性;后掠机翼;抛物化稳定性方程
0 引 言
机翼是飞机的重要部件之一,其最主要作用是产生升力,同时也产生一部分阻力。气流在机翼表面的流动状态是层流还是湍流直接决定了摩擦阻力的大小。研究结果表明层流翼型的阻力比湍流翼型的阻力可以减少一半以上。若大型运输机翼能大部分保持层流,则可节省25%的燃料,具有很高的经济价值[1]。深入理解后掠机翼的转捩机理、预测转捩位置对气动力计算和翼型优化设计是非常必要的,对机翼的气动减阻有着重要的经济价值。
后掠机翼的边界层是典型的三维边界层,其主要特点是在边界层外缘势流流速的横向有压力梯度。因此,边界层内的横向速度不为零,称为横流。横流的速度剖面存在拐点,因此流动是不稳定的,即所谓横流不稳定性。横流不稳定性的本质和T-S波不同,T-S波的产生依靠粘性。除了不稳定行进波外,横流不稳定性还可能产生不稳定的定常涡。通常在背景扰动较小时,定常涡起主导作用,在背景扰动较大时,行进波在起主导作用。
早在十几年前,机翼横流不稳定性和转捩问题就是国外研究的热点,如Malik[2-3]、Saric[4]、Haynes[5]等人的工作。近五年,除了横流不稳定性机理的研究外,添加粗糙度或吹吸的人工方法对横流和转捩位置进行控制是热点,如Mack[6]、Guha[7]等研究了横流不稳定性与压缩性、Couette不稳定性的关系,Chernoray[8]采用实验的方法、Li[9]采用抛物化稳定性方程(PSE)、Nishino[10]和Rizzetta[11]采用直接数值模拟(DNS)方法研究了粗糙度对横流不稳定性的影响和转捩位置的控制。
近五年国内大部分的研究工作是横流不稳定性机理和转捩预测,如杨永等人[12-13]在采用升华法测量转捩位置的基础上,结合线性稳定性理论(LST)做了一系列的转捩控制实验,王运涛[14]、钱炜祺[15]、陈奕[16]采用不同的湍流模式研究了翼型转捩的特点和转捩位置的预测,张坤[17]、左岁寒[18]通过线性稳定性分析(LST)、线性抛物化稳定性方程(LPSE)研究了横流不稳定性,徐国亮[19]采用非线性抛物化稳定性方程(NPSE)研究了曲率对机翼边界层二次失稳的影响。
转捩预测eN方法的理论基础是线性稳定性理论。线性稳定性分析方法可以分为两类,一类是求解经典的O-S方程,即线性稳定性分析(LST),归结为特征值问题,另一类是求解线性抛物化稳定性方程(LPSE),归结为初值问题。
借鉴LPSE方法,本文对LST进行了改进,提出用扩展的O-S方程(EOS)来进行稳定性分析的方法。该方法仍然是求解特征值问题,部分考虑了边界层内非平行流等因素对扰动幅值演化的影响。然后结合LST、EOS、LPSE和eN方法研究展向无限长的后掠机翼稳定性特性、扰动演化规律及转捩机理,对转捩位置进行预测。
1 数值方法
1.1 基本流场
采用CFD软件计算后掠翼的三维流场,其中x方向为机翼弦长方向,z方向为机翼展向方向,远离机身为正。收敛后,取展向均匀区域的流场截面,重新划分并加密网格,其中流向方向沿机翼剖面的弧线方向,采用变间距网格,机翼两头密中间稀;法向方向的网格全部垂直于机翼壁面,y的大小定义为坐标点到壁面的距离。采用直接数值模拟(DNS)的方法计算收敛后得到后掠翼的基本流场。
1.2 经典的O-S方程(LST)



在正交曲线坐标系下,考虑流向曲率drx和展向曲率drz,将N-S方程写成扰动形式,并进行线化就得到了经典的O-S方程。采用2点4阶的Malik差分法,将O-S方程离散后得到特征关系式:


1.3 扩展的O-S方程(EOS)
考虑,且基本流是x的函数将NS方程写成扰动形式,并进行线化就得到了扩展的O-S方程,离散后得到特征关系式:


1.4 线性抛物化稳定性方程(LPSE)
无论是求解经典的O-S方程还是扩展的O-S方程,都是采用某个x位置的基本流求解当地的特征值α,β,ω和特征函数φ,并对特征函数φ进行归一化,并没有考虑扰动幅值A本身的演化。将N-S方程抛物化和线化就得到线性抛物化稳定性方程:


1.5 稳定性分析及转捩预测
在得到基本流的基础上,通过求解经典的O-S方程(LST)、扩展的O-S方程(EOS)或线性抛物化方程(LPSE),就可以得到某个扰动波的特征值α,β,ω和特征函数φ,进行稳定性分析,进而进行转捩预测。转捩预测方法常用的是eN方法,其基本概念是:若在边界层内存在各种频率的小扰动,这些扰动向下游传播过程中,当其进入各个扰动相应的不稳定区域时,扰动的幅值会被逐步放大,将各个频率的扰动从其幅值开始放大的位置起,沿传播路径累计其幅值的放大倍数en,取对数后为n值。在所有扰动中,若有某一扰动的幅值放大倍数的对数最先达到预设值N时,则可判定转捩发生。该方法的理论基础是线性稳定性理论,而作为转捩判定的域值N,则是由大量的实验和计算数据相结合给出。
在本问题中,扰动演化是空间模式,因此ω为实数。展向为无限长,流场在展向均匀,仅在流向变化,因此扰动仅在流向有变化,故β为也实数,而α=αr+iαi为复数。给定β和ω,通过LST、EOS或LPSE方法就可以得到不同流向位置下的αi,积分得到eN方法中的n值:

其中x0为扰动开始增长的位置或参考位置,积分到该扰动开始衰减,即-αi<0。改变β和ω,求出n(β,ω,x)的包络值,得到转捩位置的N值:

1.6 物理模型
选用NACA0012翼型,弦长1m,厚度0.12m,后掠角25°,迎角0°。取高空10000m处无量纲参数,温度223.3K,密度0.4134kg/m3,粘性系数1.4579× 10-5Pa·s,来流Mach数0.8,单位Reynolds数6.79 ×106/m,无量纲长度1mm,无量纲Reynolds数6790。下文除非特殊说明,均为无量纲量。
2 结果分析
2.1 网格及基本流场
用有限长度机翼的流场代替无限长机翼的流场。计算发现展向前缘的影响长度大约是弦长的2倍,后缘影响的长度大约是弦长的0.5倍,本文选取展向长度为弦长的4倍。图1(a)给出了CFD整体网格示意图,在32位系统中网格达到最大值70万,在64位系统中网格为250万。取出机翼展向均匀区域的流场截面,重新划分并加密网格。图1(b)给出了加密后局部网格示意图。在流向,靠近机翼头部的间距Δx<0.1,在机翼中部的间距Δx<1;在法向,1个边界层内有100个网格点,壁面处网格间距Δy<0.008,确保网格满足稳定性分析的需要。

图1 计算网格Fig.1 Computational grid
图2(a-c)给出了机翼头部不同x位置基本流的速度剖面u、v、w沿y方向的分布,其中u和w是平行于当地壁面沿流向和展向的速度分量,v是垂直于当地壁面沿法向的速度分量。可以看出在y>1以上的速度u和w的剖面接近于常数。在机翼头部出现了加速效应,边界层外的速度u随着x的增大而增大,而速度w在边界层外接近于常数,即来流速度在展向的分量。法向速度分量v要比流向速度u小2个量级,满足局部平行流假设的要求。图2(d)给出了边界层名义、排移和动量厚度沿流向的分布曲线。在x=100处的边界层名义厚度约为0.4mm,排移厚度约为0.2mm。机翼前部分的边界层名义厚度是毫米量级。

图2 基本流的速度剖面和边界层厚度Fig.2 Pr of ile of mean flow and boundary layer thickness
2.2 特征值和特征函数
表1给出了采用LST、EOS、LPSE三种方法计算出来的不同流向位置的特征值。可以看出EOS计算出的幅值增长率-αi略大于LST的计算结果,而LPSE的结果比LST的结果要大30%左右,表明对无限长后掠翼而言,除了扰动波特征值-αi引起的幅值增长外,还需要考虑幅值本身的增长。

表1 扰动波(β=2.0,ω=0.05)的增长率Table 1 Growth rate of the wave(β=2.0,ω=0.05)
图3(a)给出了扰动波(β=2.0,ω=0.05)在x=150.7处的特征函数沿法向的分布。速度|u|的最大值远离壁面,在边界层排移厚度外,属于第一模态的不稳定波。通过LST和EOS计算得到的特征函数符合的很好。图3(b)给出了该扰动波的幅值增长曲线,同样可以看出LPSE的结果要比EOS和LST的结果大很多,LST和EOS的幅值最大增长值n在5左右,而LPSE的结果达到了8左右。说明非平行性效应在机翼头部必须考虑。

图3 扰动波(β=2.0,ω=0.05)的特征函数和幅值演化曲线Fig.3 Eigen-function and growth curve of the wave(β=2.0,ω=0.05)
2.3 中性曲线和最大增长率
图4(a)给出了LST得到的不同β的(x,ω)平面上的中性曲线,即在该线上αi=0。本文中取x0=25作为稳定性分析的开始位置。对于平板边界层,中性曲线有上下两支,并且存在一最小的位置xcr,在该位置上下两支重合,形成一个类似于大拇指的外形,也称为拇指曲线。在中性曲线内,αi<0,扰动波是增长的,在中性曲线外,αi>0,扰动波是衰减的。不同于平板边界层,有后掠角的机翼边界层不一定存在下支中性曲线。
从图4(a)可以看出,当β=4.0时,中性曲线呈半开放式,即在中性曲线的左边,αi<0,扰动波都是增长的,而在中性曲线的右边,αi>0,扰动是衰减的。随着β的减小,中性曲线出现左半支,在左半支和右半支之间扰动波是增长的,之外是衰减的,但是仍然没有下支。不同的β,在一定的x范围内,出现了ω=0的扰动波是增长的,即出现不稳定的驻波。从图4(a)可以看出,当β=4,x<150,而当β=2.5、2.0和1时,在x<300的位置都出现了增长的驻波,是典型的横流不稳定性问题。
图4(b)给出了不同ω的(x,β)平面上的中性曲线。不同的ω,存在上、下两支中性曲线,但是两支曲线在右边重合封闭,而向左边是开口的,形成一个反拇指的形状。而且在频率ω从0到0.10的范围内,在x<200位置的中性曲线非常接近,表明在这个范围内的扰动都是增长的。外界扰动进入边界层后将直接被放大。

图4 中性曲线Fig.4 Neutral curve
图5(a)和(b)分别给出了不同β的最大增长率-αi和相应的ω。从图5(a)可看出,当β=4时,越靠近前缘最大增长率-αi越大,最大能到0.085,相应的ω也越大,超过了0.20,但是增长的范围较小,在x<150以内。当β=2.5、2和1时,最大增长率小于0.04,但是增长的范围很宽,从x=50到x=400,而且当x>150后最大增长率曲线重合的很好,不同的展向波数β在该范围内的最大增长率相同。从图5(b)可以看出最不稳定的扰动波的频率在ω=0.05附近。

图5 最大增长率和相应的频率Fig.5 Maxinum growth rate and its corresponding frequence
2.4 扰动波的幅值演化曲线
图6(a)给出了LST计算得到的不同扰动的幅值演化曲线,可以看出,当扰动频率相同时,首先是展向波数β大的扰动波先增长起来,随着往下游的演化,到一定位置又开始衰减,展向波数β小的波也逐渐增长起来,并且增长的指数n逐步超过波数大的扰动。由于中性曲线向左是开口的,这些扰动在开始积分的起点位置x0=25处都是不稳定的,因此所有扰动从积分起点就开始增长。EOS和LPSE的计算结果与LST的一致,仅仅是扰动曲线幅值n的大小不同。图6(b)给出了LPSE的计算结果,趋势与LST相同,不同的是增长幅度n值要大。
2.5 转捩预测
给定扰动的展向波数β和频率ω就能得到一条幅值演化曲线,这些幅值演化曲线的包络线就是转捩预测eN方法中N值曲线。从图4可以看出幅值演化曲线能达到最大值的扰动波的展向波数范围为0.5到8,频率范围为0到0.5。本文中取波数间隔为0.1,频率间隔为0.05,计算了全部扰动波的幅值演化曲线,在每个位置上取全部扰动波中最大的n值,作为该处的包络值N。
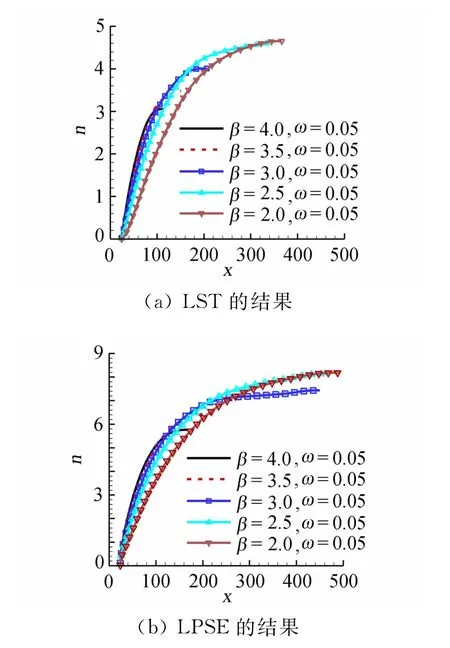
图6 幅值增长曲线Fig.6 Growth curve
图7给出了基于LST、EOS、LPSE三种方法得到了包络曲线,其中线条表示所有扰动波的包络线,而符号表示驻波的包络线。可以看出采用LST方法预测的N值相对EOS和LPSE的值偏小,最大值小于5,EOS的结果略大于LST的结果,最大值接近5,而LPSE的结果比LST和EOS均要大,最大值接近9。

图7 转捩预测方法eN中的N值Fig.7 N-factor in eNmethod
在后掠机翼中存在横流不稳定性,其扰动波的波矢方向跟主速度矢量方向垂直,而且扰动频率很小,接近于0,常以驻波的形式出现。对比所有扰动波的包络线和驻波的包络线,可以看出,横流不稳定波的预测N值略小,表明横流不稳定性占主导作用。
采用LPSE的方法预测的转捩N值达到了9,表明转捩位置在机翼的前缘。实际的转捩位置跟感受性问题有关,取决于外界扰动进行边界层后的扰动展向波数、频率和幅值大小。不同的x位置,对应的N值不同,相应的最不稳定波的展向波数和频率也不同。研究结果表明,如果扰动波的无量纲的幅值达到20%就发生转捩了[20]。表2给出了x=50、100和200位置处发生转捩时的N值及其可能引发转捩的扰动波的展向波数β、频率ω和在x0=25处的扰动幅值u0。

表2 在x处发生转捩时(u=0.2U∞)的N值,以及引起转捩发生的扰动波的波数β、频率ω和在x0=25处的幅值u0(m/s)Table 2 N-factor at the transition location x where u=0.2U∞,and the wave numberβ,frequencyωand the amplitude u0(m/s)at x0=25 of the inducing wave
以LST的计算结果为例,如果展向波数为4,频率为0.15的扰动波进入了x0=25处的幅值为7.93m/s,那么该扰动传播到达x=50位置时的幅值将被放大e1.8=6倍,即48.8m/s,达到了来流速度U∞=240m/s的20%,可以认为转捩发生了。而EOS和LPSE的计算结果表明在x0=25处的幅值分别为5.88m/s和2.16m/s就能在x=50处引发转捩。而若转捩在x=200处发生,LST、EOS、LPSE三种方法计算出扰动在x0=25的幅值仅为0.65m/s、0.36m/s和0.04m/s。
从表2还可以看出,虽然三种稳定性分析方法获得的N值不完全相同,但预测的最可能引发转捩的扰动波的展向波数在3.0到3.5之间,频率在0.035到0.060之间,相应的展向波长为约为2mm。
3 结 论
本文在采用CFD和DNS相结合的方法计算得到无限长后掠翼基本流的基础上,通过求解经典的O-S方程(LST)、扩展的O-S方程(EOS)和线性抛物化稳定性方程(LPSE)进行稳定分析和转捩预测,得到以下结论:
(1)后掠翼在(x,ω)平面上的中性曲线没有下支,在(x,β)平面上的中性曲线呈反拇指的形状,横流不稳定性在机翼前缘占主导作用。
(2)当外界扰动进入边界层后,幅值将被直接放大,首先是展向波数β大的扰动波增长起来,然后是波数β小的波逐渐增长起来,并且增长的指数N逐步超过波数大的扰动。
(3)转捩在机翼前缘完成,引起转捩的扰动波的展向波长约为2mm。
[1]周恒,赵耕夫.流动稳定性[M].北京:国防工业出版社,2004.
[2]MALIK M R,LI F,CHANG C L.Crossflow disturbances in three-dimensional boundary layers:nonlinear development,wave interaction and secondary instability[J].J.Flutd Mech.,1994,268:1-36.
[3]MALIK M R,LI F,CHOUDHARI M M,et al.Secondary instability of cross-flow vortices and swept-wing boundary-layer transition[J].J.Flutd Mech.,1999,399:85-115.
[4]SARIC W S,CARRILLO J R,REIBERT M S.Nonlinear stability and transition in 3-D boundary layers[J].Meccantca,1998,33:469-487.
[5]HAYNES T S,REED H L.Simulation of swept-wing vortices using nonlinear parabolized stability equations[J].J.Flutd Mech.,2000,405:325-349.
[6]MACK C J,SCHMID P J,SESTERHENN J L.Global stability of swept flow around a parabolic body:connecting attachment-line and crossflow modes[J].J.Flutd Mech.,2008,611:205-214.
[7]GUHA A,FRIGAARD I A.On the stability of plane Couette-Poiseuille flow with uniform crossflow[J].J.Flutd Mech.,2010,656:417-447.
[8]CHERNORAY V G,DOVGAL A V,KOZLOV V V,et al.Secondary instability of a swept-wing boundary layer disturbed by controlled roughness elements[J].Journal of Vtsualtzatton,2010,13(3):251-256.
[9]LI F,CHOUDHARI M M,CHANG C L,et al.Computational modeling of roughness-based laminar flow control on a subsonic swept wing[J].AIAA Journal,2011,49(3):520-529.
[10]NISHINO T,SHARIFF K.Direct numerical simulation ofa swept-wing boundary layer with an array of discrete roughness elements[A].Seventh Iutam Symposium on Laminar-Turbulent Transition[C],2010,18:289-294.
[11]RIZZETTA D P,VISBAL M R,REED H L,et al.Direct numerical simulation of discrete roughness on a sweptwing leading edge[J].AIAA Journal,2011,48(11):2660-2673.
[12]杨永,左岁寒,李喜乐,等.基于升华法实验研究后掠翼三维边界层的转捩[J].实验流体力学,2009,23(3):40-43.
[13]左岁寒,杨永,李栋,等.后掠翼边界层横流不稳定性的实验研究(英文)[J].空气动力学学报,2010,28(5):495-502.
[14]王运涛,王光学,张玉伦.30P-30N多段翼型复杂流场数值模拟技术研究[J].空气动力学学报,2010,28(1):99-103.
[15]钱炜祺,RANDOLPH C,LEUNG K.考虑转捩影响的翼型动态失速数值模拟[J].空气动力学学报,2008,26(1):50-55
[16]陈奕,高正红.Gamma-Theta转捩模型在绕翼型流动问题中的应用[J].空气动力学学报,2009,27(4):411-418.
[17]张坤,宋文萍.基于线性稳定性分析的e~N方法在准确预测翼型气动特性中的应用[J].西北工业大学学报,2009,27(3):294-299.
[18]左岁寒,杨永,李栋.基于线性抛物化稳定性方程的后掠翼边界层内横流稳定性研究[J].计算物理,2010,27(5):665-670.
[19]徐国亮,符松.曲率对机翼边界层二次失稳影响[J].力学学报,2010,42(6):995-1005.
[20]黄章峰,曹伟,周恒.超音速平板边界层转捩中层流突变为湍流的机理-时间模式[J].中国科学,G辑,2005,35(5):537-547.
Cross-flow instability analysis and transition prediction of airfoil boundary layer
HUANG Zhangfeng1,2,LU Xuezhi1,YU Gaotong1
(1.Department of Mechanics,Tianjin University,Tianjin 300072,China;2.State Key Laboratory of Aerodynamics,Mianyang Sichuan 621000,China)
Cross-flow instability analysis and transition prediction have been done on a 25°swept,0°attacked airfoil with Mach number 0.8,unit Reynolds number 6.79×106/m by solving the classic O-S equation(LST),extended O-S equation(EOS)and linear parabolic stable equation(LPSE)together with theeNmethod.Results show that the lower branch of the neutral curve in(x,ω)plane does not exist and the shape of the neutral curve in(x,β)plane appears as an anti-thumb.The cross-flow instability plays a key role in the leading edge.As disturbances enter the boundary layer,their amplitude will be enlarged directly.For the same frequence,the disturbances with big wave numberβwill grow firstly and propogate to a certain place where they begin to decay,then the disturbances with small wave numberβincreased gradually and their increasing factorNwill exceed that with big wave number finally.Transition occurs in the leading edge of the airfoil and the wave lengh of the inducing wave is about 2mm.
instability analysis;transition prediction;cross-flow instability;swept airfoil;parabolic stable equation
V211.1+9;O357.4+1
A doi:10.7638/kqdlxxb-2012.0062
0258-1825(2014)01-0014-07
2012-08-20;
2012-11-15
空气动力学国家重点实验室开放课题资助(SKLA201101,SKLA201201)
黄章峰(1977-),男,湖南宜章人,副教授,研究方向:流动稳定性、转捩及湍流、直接数值模拟.E-mail:hzf@tju.edu.cn
黄章峰,逯学志,于高通.机翼边界层的横流稳定性分析和转捩预测[J].空气动力学学报,2014,32(1):14-20.
10.7638/kqdlxxb-2012.0062.HUANG Z F,LU X Z,YU G T.Cross-flow instability analysis and transition prediction of airfoil boundary layer[J].ACTA Aerodynamica Sinica,2014,32(1):14-20.

