数学练习的“拓展”思考

应苏玲

数学练习是每一节数学课必备的一个环节，在实际的教学中，许多教师多注重新授知识的教学，往往忽略了对课堂练习的设计与处理，致使比较低效甚至无效的作业练习在教学中普遍存在. 因此，针对当前的这种情况，我觉得有必要对课堂教学进行“刷新”，我们应该给数学练习进行彻底的“拓展”.

方法一：由“超前性”向“同步性”拓展

数学练习的设计必须和课堂教学保持一致，因为学生的思维是受课堂教学而驱动的. 学生一节课大约有25分钟的思维活动时间用来学习新知，每节课一般只学习一个或两个新的知识点，新的知识结构在学生的头脑中已经基本成型. 新、旧两种知识形成阶梯，学生借助新、旧知识作为“扶手”，能够登攀一至两个台阶. 若练习设计深了一步，无“扶手”可抓，学生则很容易“摔倒”.

方法二：由“无序性”向“层次性”拓展

在课堂练习中，许多教师只是按部就班，按照教材的顺序一题一题地往下讲，根本不注意学生的认知发展规律. 心理学研究表明，小学生的数学学习有其独特的规律，小学生数学学习的认识过程大致要经历三个层次：凭借旧知来同化新知；将新知类化纳入到原有的知识结构中；在相应的情境中运用提升. 因此，我们在设计数学练习的时候，应遵循学生的认知规律，要了解学生知识的掌握情况，设计一些有效的、有针对性的练习. 在设计练习时还要注意层次性，要兼顾到班级群体和个体之间的差异性.

例如，在教学“分数大小比较”时，我设计了以下四组练习. 比较下面各组分数的大小：（1）和；（2）和；（3），和；（4）和. 这四组题目难度各异，逐级递进，符合学生的认知规律. 这样的练习设计，具有一定的层次性，促进了不同认知水平的学生都有不同的发展.

方法三：由“呆滞性”向“灵活性”拓展

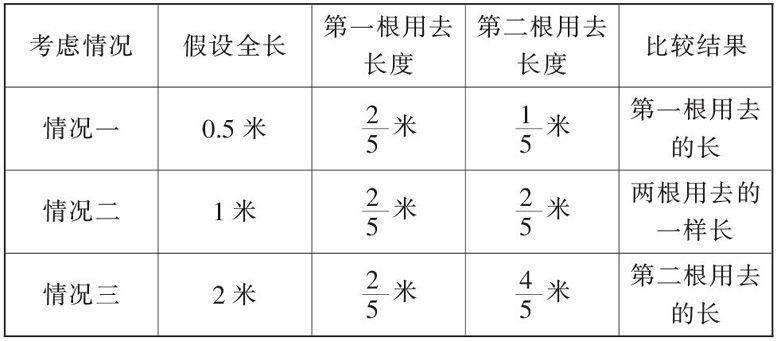
《数学课程标准》指出：动手实践、自主探索、合作交流是学生学习数学的重要方式. 传统的练习一般具有如下的缺点：呆板、枯燥、繁琐. 学生往往是为了做题而做题，没有一定的思维活动空间. 如果设计的练习题具有灵活性，学生就会有动手实践的机会，也会有自主探索的空间，学生之间还会有合作交流的余地. 我们教师应改变那种传统的模仿或示范练习的教学方式，要引导学生投入到探索与交流的活动中来. 例如，教学这样一道思维题：两根同样长的钢管，第一根用去■米，第二根用去，哪一根用去的长一些？这道题目就比较灵活，在解答时，我们要考虑第二根钢管的变化，第二根用去的长度是随着全长的变化而变化的，因而是不确定的. 要知道哪一根用去的长一些，要进行分类讨论. 可以让学生先小组合作交流，然后共同探索解题的策略. 在交流汇报时，教师可以引导学生利用假设法列表比较：

方法四：由“封闭性”向“開放性”拓展

国际数学教育委员会曾撰文指出：在数学课堂里更多地进行没有固定答案的研讨，会使更多的学生体会到数学的美感. 因此，在教学中增强数学练习的开放性，鼓励学生探讨开放性问题，有利于培养学生的创新意识. 增强练习教学的开放性，一是要让学生参与练习的形成过程，可以在练习过程中现场采集数据或让学生提供练习的素材，也可以让教师提供不完备的练习题材，让学生共同参与形成练习的习题. 二是要设计合适的开放题，开放题的形式可以是条件开放、问题开放、解题策略开放等.

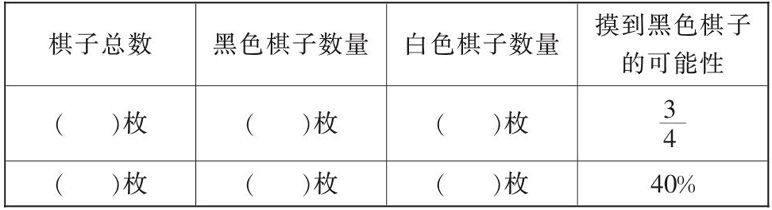
例如，“用分数表示可能性的大小”教学后，我设计这样的一道开放题：在口袋里放黑色和白色棋子，任意摸一摸，要符合表中的要求，可以怎样设计？把你的设计填在下面的表中.

这样的开放题有利于学生创新潜能的发挥和创新个性的形成，有利于学生体会数学的应用价值，能有效地预防思维定式，拓宽学生的思路，促进高层次思维的发展，开发学生的创造潜能. 另外，设计开放题要注意适时性和适用性，不要过多过滥，同时要使用到位，真正发挥每一道开放题的价值.

方法五：由“课内”向“课外”拓展

所谓“调查型”作业就是让学生进行社会小调查，通过探究、讨论来分析计算调查结果，得出其所需结论的一个实践过程，再运用已有的知识来解决实际问题. 让学生在生活中进行数学调查，培养了学生的探索能力，增进了学生的数感意识. 如学习了“升和毫升”后，就让学生去超市或家中进行调查，看看哪些物品是用升和毫升作单位的，并将其结果记录下来. 《数学课程标准》中也有一个很好的范例：请调查一天内你家丢弃多少个塑料袋，一周呢？一月呢？一年呢？全班学生一年大约丢弃多少个塑料袋？全校学生呢？你能针对塑料袋问题向环保部门提个建议吗？……这些有趣又紧密联系学生生活实际的数学问题不仅激发了学生探索的意识，还将数学知识与其他学科进行了有效的结合，有利于学生综合素质的提高.