浅谈分数应用题的解法

张克

稍复杂的求一个数的几分之几是多少的应用题和已知一个数的几分之几是多少，求这个数的应用题是小学阶段最抽象、学生最难理解的数学知识之一，也是学生最容易混淆的内容之一。怎样帮助学生学好分数应用题，是摆在我们数学教师面前的一项重要任务，我们必须认真钻研教材，领会教材的编写意图，鼓励学生积极参与教学活动，真正使学生学会、理解稍复杂的分数应用题的解法。

一、让学生用不同思路解答稍复杂的分数应用题，使解题方法多样化

为了便于比较，以下面两道题为例来说明：

（1）4年（1）班有男生30人，女生比男生多1/5 ，女生有多少人？

（2）4年（2）班有女生36人，比男生多1/5 ，男生有多少人？

1. 用解整数应用题的思路来解分数应用题。

（1）出示上面两道题，让学生说说这两道题有什么相同点和不同点。

相同点：这两道题都是把男生人数看作单位“1”，两道题的第二个条件相同。

不同点：第一题单位“1”的量是已知的，第二题单位“1”的量是未知的。

（2）画线段图分析

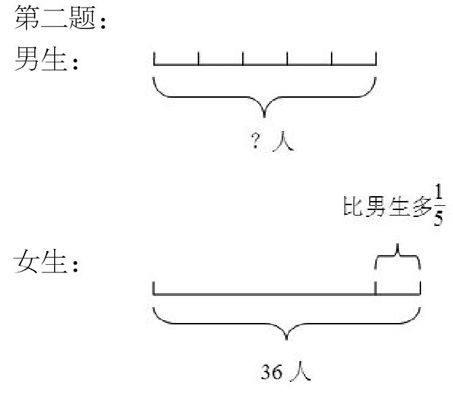
第一题：

男生：

把男生人数看作单位“1”，则可列出等式：男生人数加上女生比男生多的人数等于女生人数。即：男生人数+男生人数×1/5 =36，然后列方程解答。解：设男生有X人，X+ 1/5 X=36，X=30。

用解整数应用题的思路解分数应用题是从学生已有的知识和经验出发来学习新知识，符合学生的认知规律，便于学生接受和理解新知识。

2. 用较新的思路来解分數应用题。第一题：把男生人数看作单位“1”，女生人数相当于男生人数的（1+ 1/5 ），求女生有多少人，就是求30人的（1+ 1/5 ）是多少，列式为30×（1+ 1/5 ）=36（人）

第二题：把男生人数看作单位“1”，女生人数相当于男生人数的（1+ 1/5 ），也就是男生人数的（1+ 1/5 ）是女生人数，即：男生人数×（1+ 1/5 ）=36，根据这个等式可以列方程解答。解：设男生有X人，（1+ 1/5 ）X=36，X=30;也可以根据除法的意义用算术方法解，36÷（1+ 1/5 ）=30（人）。

这是一种比较新的思路，它是建立在一个数乘以分数的意义的基础之上的，只要学生理解了一个数乘以分数的意义，也就能够理解这种解题思路。

3. 用整数列式解分数应用题。第一题：把男生人数看作单位“1”，把男生人数平均分成5份，则女生人数比男生多1份，即5+1=6份，先求1份有多少人，再求6份有多少人，列式为30÷5×（5+1）=36（人）。

第二题：分析同上题，先求1份有多少人，再求5份有多少人，列式为36÷（5+1）×5=30（人）。

这种解题思路虽然不是教材所提倡的，但是对一些学困生来说学会这种解题思路也是有益的。

二、抓住两种类型分数应用题之间的内在联系，巧解分数应用题

从上面两道题可以看出，两种类型分数应用题具有相同的基本结构，只不过是已知条件和所求问题变化了，二者的解题思路基本上是一致的，它们具有共同点，是一个数乘以分数的意义，把二者联系起来，因此我们在教学中要引导学生分析这两种类型分数应用题中的数量关系，弄清它们之间的内在联系，进而从整体上把握其解题规律。

如从第一题和第二题的第二个条件中，都能很容易得出这样的数量关系，男生人数+男生人数×1/5 =女生人数，或男生人数×（1+ 1/5 ）=女生人数，然后把已知条件分别代入上面的等式中。即：

第一题：30+30×1/5 =女生人数，或30×（1+ 1/5 ）=女生人数，这样可以直接求出女生人数。

第二题：男生人数+男生人数×1/5 =36，或男生人数×（1+ 1/5 ）=36，根据这两个等式可以列方程或用算术方法求出男生人数。

通过上面对两道题的分析可知：任何一道求一个数的几分之几是多少的应用题和已知一个数的几分之几是多少，求这个数的应用题，都可以写成一个具体的数量关系式，然后把已知条件代入关系式中，便能求出答案。

三、交给学生通俗易懂的解题方法，切忌死记硬背

有的教师在教学上面的两种类型应用题时，常常引导学生总结所谓的解题方法，即：如果单位“1”的量是已知的用乘法列式;如果单位“1”的量不是已知的，列方程或用除法列式。

这是交给学生一种死记硬背的解题方法，一部分学生特别是学困生并没有理解，只能暂时记住这种方法，过一段时间这样的题又开始混淆了，显然这样的教学是不成功的。

我们在教学中应结合学生的学习活动，引导学生总结出通俗易懂的解题方法，使学生不但会用而且会讲，说出其来源，这样学生才是真正地理解了所学知识。

总之，我们在教学中应不断的更新教育观念，改革教学方法，积极引导学生参与教学活动，让学生概括应用题的解题规律，总结解题方法，并知其来龙去脉，真正使学生灵活自主地学习数学知识。