股市收益率涨跌不对称性的区间分析

方立兵,刘 烨

（南京大学 工程管理学院,南京 210093）

0 引言

股市收益率涨跌变化的不对称性已经引起人们的广泛关注。在资产定价领域，收益率的不对称性是三阶矩（偏度）风险的主要衡量内容；在衍生品定价领域，这一特性意味着均值两侧未来支付存在多大的差异；在风险管理领域的重要性则更为明显，涨跌的不对称性意味着同一资产多头和空头头寸的风险并非一致的。鉴于此，进一步分析收益率涨跌的不对称特征在不同的分位数区间具有怎样的差异，有助于深刻认识收益率的分布特征，进而为资产定价、衍生品定价和风险管理提供借鉴。特别对于风险管理而言，明确收益率分布的不对称性在哪个区间更加严重，将有助于实现对多头和空头头寸的风险进行更加细致的差异化管理。

1 模型方法

2 实证分析

2.1 样本说明

本文的实证研究选取沪深指数1998年1月1日至2011年5月31日的百分比对数日收益率为样本。选取市场指数收益率为研究对象的重要意义在于，市场指数收益率是分散较为充分的组合，其收益率条件偏度的存在性更有助于支持偏度风险的系统性。样本的描述性统计结果如表1所示。

从表1可以看出，两市的指数收益率均存在显著的负偏度和超额峰度，Jarque-Bera检验也显著拒绝了正态分布的原假设。从中位数和均值的相对大小可以看出，中位数在均值的右边，这说明收益率分布的左尾长于右尾。因此，描述性统计初步说明上证指数的收益率在左右两侧的分布是存在差异的。特别的，深证综指的负偏斜程度比上证指数更加严重。当然，这一比较结果未考虑收益率波动的聚集性和持续性等典型事实的影响。

2.2 半参数EGARCH模型的估计

表1 沪深指数1998年1月1日至2011年5月31日收益率的描述性统计

表2 基于EF方法的EGARCH模型拟合的沪深两市标准化收益率

从表2可以看出，经EF-EGARCH模型拟合后的标准化收益率仍然存在显著的负偏度和超额峰度，Jarque-Bera检验显著拒绝了正态性。其次，从位置参数来看，两市标准化收益率的中位数远大于样本均值，这与负偏度的分布形态是一致的。由此可见，表2的描述性统计结果显示，两市的标准化收益率仍然存在显著的负偏特征。

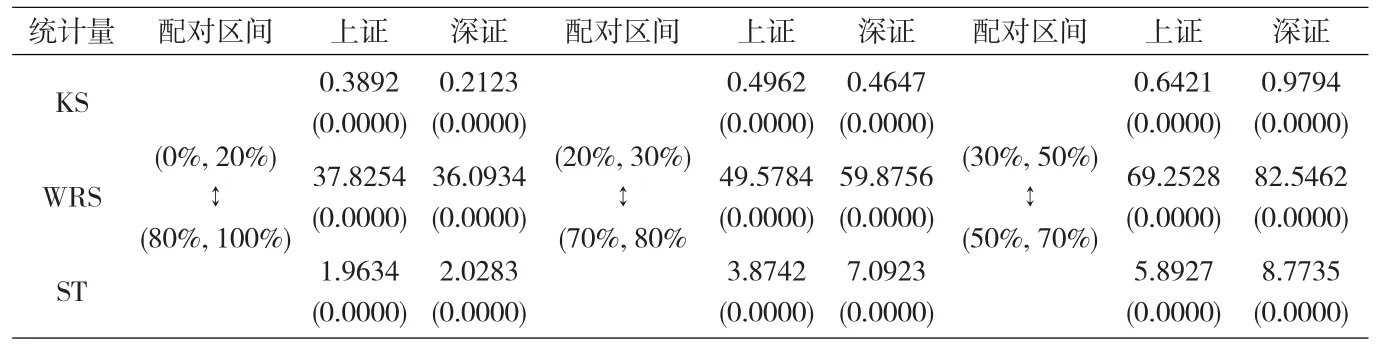
表3 基于三种非参数统计量对收益率均值两侧的对称性进行区间分析

2.3 基于核密度估计的区间分析

进一步采用核估计方法检验对标准化收益率的非对称特征进行区间分析。考虑将均值两侧核密度估计结果按照 (q0，q1)=(0%,20%)、(20%,30%)和(30%,50%)分成三段，并进行比较。当然，这三个区间段只是作为本文应用的一个例子，实际应用中可以根据研究所涉及的问题背景确定。图1给出了上证标准化收益率的结果。限于篇幅，且深证综指的结果与上证指数类似，因此不再给出。

图1 上证EGARCH收益率均值两侧核密度分布之比较

从表3的结果可以看出，三种非参数统计量的检验结果均显示，基于EF-EGARCH获得的标准化收益率，在其均值两侧的核密度具有显著差异。其中，深证综指的核密度在均值两侧的差异相对较大，这与表2的描述性统计的结果显示深证综指具有更加严重的负偏度是类似的。另外，与图2的直观展示结果类似，表3也显示，标准化收益率在均值的非对称性随着分位数水平 (q0，q1)取(0%,20%)、(20%,30%)和(30%,50%)，均值两侧的核密度差异越来越大。因此，可以认为收益率非对称性在均值两侧的中间部分更加严重。

3 结论

本文基于核密度估计和估计函数方法提出了一种对收益率涨跌不对称性的区间分析方法。与现有的方法相比，该方法模型风险相对较小，且可以更为细致地考察条件分布的不对称性来自分布的哪个区间。以沪深两市的日收益率为样本，在收益率服从指数GARCH模型的假设下，采用效率较高的估计函数方法获得了两市的半参数标准化收益率，并采用核密度方法对其不对称性进行区间分析。以(0%,20%)、(20%,30%)和(30%,50%)三个分位数区间为例，收益率分布的不对称性在(30%,50%)以及(50%,70%)两个区间最为严重。这一现象预示着，收益率分布的不对称性在均值两侧的中间部分最为严重。这一研究结果对于资产价格的风险管理具有重要意义。市场风险管理常常针对的是价格的大幅变动。本文的研究结果预示着，价格的小幅变动（均值两侧的中间部分）应着重关注涨跌的不对称性。

[1]Li D X,Turtle H J.Semiparametric ARCH models：An Estimating Function Approach[J].Journal of Business&Economic Statistics,2000,18(2).

[2]Silverman B W.Density Estimation for Statistics and Data Analysis[M].London：Chapman&Hall,1986.