基于遗传神经网络的独立机构投资者持股偏好研究
李辰颖,田治威,杨海燕
(1.北京林业大学,北京100083;2.广西大学,南宁 530004)
0 引言
资本市场上活跃的两大投资主体分别为个人投资者和机构投资者,机构投资者与个人投资者相比,其投资管理更加专业化、投资结构呈现组合化、投资行为更加规范化,也能够在促进证券市场稳定、健康及完善等方面发挥较大的作用,因而机构投资者对于上市公司和资本市场都是非常重要的,也正因如此,机构投资者持股行为特征一直是理论界和实务界的热点话题之一。
通过总结国内外文献的回顾与对比可以发现:(1)国内关于机构投资者持股特征的实证研究还相对较为缺乏,特别是独立机构投资者持股特征的实证研究;(2)从研究方法来看大多数研究集中在多元线性回归分析甚至是单变量分组检验,这样的处理一方面忽略了机构投资者持股数量或比例与持股影响因素之间可能的非线性关系,另一方面将诸多的持股影响因素代入多元线性回归模型可能会影响模型的精度,从而影响分析结论的稳定性。为解决这些问题,本文采用改进遗传神经网络和平均影响值方法研究独立机构投资者持股比例持股偏好。
1 研究思路及变量的选取
1.1 研究思路
本文的研究思路是:在选取上市公司安全性、盈利性等相关指标数据及独立机构投资者持股比例的基础上,首先将独立机构投资者持股比例划分为高持股组和低持股组,并对选取的指标与独立机构投资者持股比例的关系采用改进后的遗传BP神经网络建模;最后在建模的基础上,采用平均影响值方法研究上市公司相关指标对独立机构投资者持股比例的影响情况。
1.2 变量的选取
依据研究目的,因变量选取了独立机构持股比例。在自变量选取上,Eakins等发现机构投资者一般倾向持有流动比率高、规模大、流动性强、支付股利、排名较高的公司。Bushee[1]分别检验了不同类型机构投资者持股公司的特征,包括公司的规模、每股账面价值、股票的市场回报率、债务水平、盈余的变化等变量,发现机构投资者偏好成长性较好的公司。Russell Reynolds Associates通过调查发现,机构投资者主要关注特征有:高管持股和高管受到外部权威独立组织评价的结果等。
通过分析可发现,学者们主要选取了反映企业安全性、营利性、成长性、股权结构以及高管受外部评价结果5个方面的特征,因此结合本研究对象目的,选取了这5个方面的10个自变量(见表1)。

表1 变量说明表
需要说明的是这里将CEO声誉作为高管受外部权威且独立组织评价的结果,是参考了Milbourn[2]的研究结论,将CEO作为高管的代表,并用媒体曝光度度量CEO声誉“量”上的积累,用按行业调整的企业绩效作为CEO声誉“质”的度量。
2 自变量与因变量模型的建立
2.1 遗传神经网络算法的改进
由于自变量与因变量之间存在非线性关系,而BP神经网络具有较好的非线性拟合能力,故采用BP神经网络进行建模,但BP神经网络在网络权值和阈值的训练中易陷入局部极小值,所以需采用有效的优化算法保证神经网络收敛到全局最优解。遗传算法相对来说具有全局优化能力,能保证BP神经网络收敛到全局最优解,故采用遗传算法对BP神经网络进行优化。在参考史峰等[3]的算法(以下称原算法)基础上,为提升原算法的精度及计算效率,对原算法进行了改进,具体步骤见图1所示。
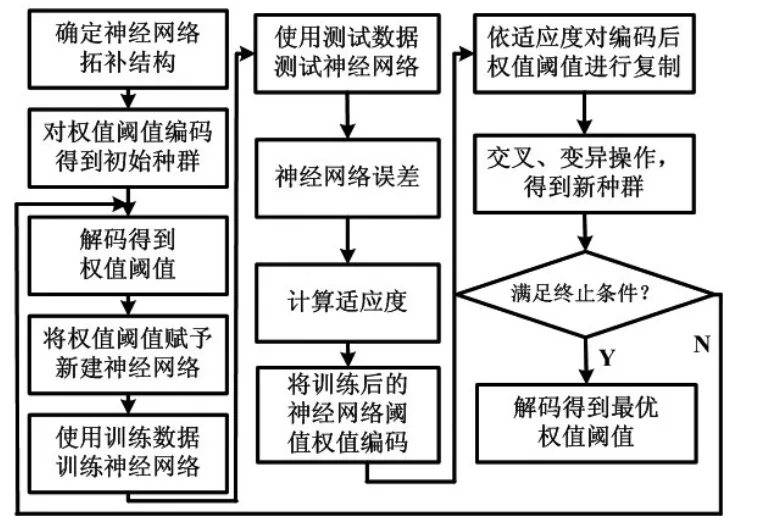
图1 改进后的遗传BP神经网络算法流程图
(1)确定BP神经网络拓补结构,包括BP神经网络的层数,隐含层神经元的个数等;
(2)将BP神经网络的权值和阈值进行编码,并随机赋值得到遗传算法的初始种群G0;
(3)解码得到权值和阈值,赋予新建的神经网络;
(4)使用训练数据训练神经网络,并用测试数据测试神经网络,得到测试误差,且计算适应度函数;
(5)将训练后的神经网络权值和阈值编码,并根据适应度函数值的大小进行复制,然后进行交差和变异操作得到新的种群Gi;
(6)若神经网络等于小于预设的误差或遗传算法达到最大进化次数,则停止计算,否则返回步骤(3);
(7)将第(6)步采用遗传算法得到的最优解解码,得到最优BP神经网络的权值和阈值。
改进后的算法与原算法的主要区别在于:在步骤5中,原算法直接对神经网络训练前的权值和阈值进行复制,变异和交叉操作得到新种群,而改进后的算法是对经过训练后的神经网络权值和阈值进行复制,变异和交差操作得到新的种群。两种算法计算过程及结果比较将在计算结果中给出。
2.2 BP神经网络设计
(1)训练数据和测试数据的选取
本文的数据来源于万德资讯中2010年沪深两市A股上市公司的相关数据,在剔除了空值之后,依据变量选取部分所述方法得到10个自变量的值及因变量的值,共计743个样本。
将2010年的独立机构投资者持股比例按中位数分为高持股组和低持股组,并定义高持股组的因变量为1,低持股组为0,然后将总样本80%的数据用于训练为训练数据,剩下的样本为测试数据。为保证神经网络收敛速度和收敛误差,对样本数据应用极差归一化公式进行了归一化。
(2)神经网络结构的确定
定义了高持股组和低持股组因变量的数值后,就将问题转化成一个分类问题。一般情况下3层BP神经网络可以很好地解决模式识别问题,故构建的BP神经网络包含输入层、隐含层和输出层3层。与自变量和因变量相对应输入、输出层神经元个数分别为10个和1个。
在确定隐含层神经元个数前需确定网络训练方法,结合本研究计算量,兼顾精度、速度及占用内存等方面情况,参考陈明忠[4]的结论,网络训练方法采用Levenberg-Marquardt算法。
在隐含层神经元个数的确定中,采用在经验公式的基础上,结合实验法的方法。首先采用经验公式n1=sqrt(m+n)+a(sqrt为平方根,n1为隐含层节点个数,m和n分别为输入和输出层节点个数,a为1~10之间的整数)确定隐含层神经元个数范围为5~15个,接着用训练数据训练神经网络,并用测试数据测试神经网络并得到网络分类错误率,错误率最小时所对应的神经元个数即为最佳隐含层神经元个数,在计算中为了克服神经网络随机初始权值和阈值带来的影响,对每个隐含层神经元个数都训练50次,并取平均值,结果如图2所示。
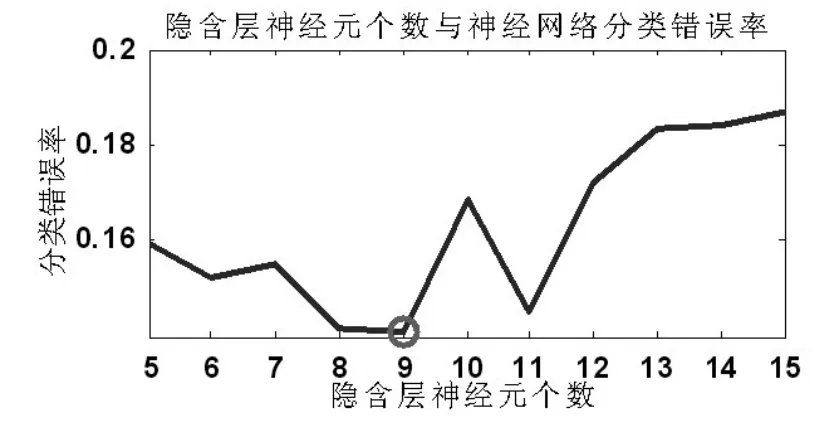
图2 隐含层神经元个数与神经网络分类错误率
从图2中可知,当隐含层神经元个数为9时,BP神经网络分类错误率最小,大约为0.14,因而隐含层神经元个数为9个。
2.3 遗传算法设计
(1)适应度函数。适应度函数定义为预测值与期望值的残差,这里用均方误差衡量。
(2)选择。根据适应度值,在当前群体中采用轮盘赌模型选择下一代,第i个个体的选择概率为

式中Ei为第i个个体适应度值,m为种群数量。
(3)交叉。本研究交叉操作为:1)随机选定第k个染色体ak和第l个染色体al;2)随机产生[0,1]区间的随机数b;3)ak和al在j位的交叉操作如下:

(4)变异。采用基本变异法,主要步骤如下:
1)设定变异概率Pm,随机选择发生变异个体;
2)将选中个体中的染色体随机位的基因,替换为符合约束条件的任意值。
此外,经反复实验并参考闫利军[5]的相关结论,设定遗传算法主要参数:最大进化次数30代,种群数量30,交叉概率0.6,变异概率0.1。
2.4 计算结果及性能分析
首先用训练数据训练改进后的遗传BP神经网络然后用测试数据测试训练好的网络,并得到网络误差和分类错误率,为了比较改进后的算法与原算法的性能,同时按原算法进行了计算。
图3为采用改进后方法得到的最优个体适应度值与进化次数关系图,从图中可以看出进化初期最优个体适应度值随进化代数增加快速下降,之后下降较为缓慢,达到最大进化次数30次时,最优个体适应度值为0.0519;图3虚线为采用原算法得到的最优个体适应度值与进化次数关系图,可看到在进化了100次之后最优个体适应度值为0.0672。通过对比易发现,改进后的算法效率较高,用了较少的进化次数就达到了比原算法还优的效果,主要原因是改进后的算法可将BP神经网络在权值阈值训练中具有方向性的优点与遗传算法具有全局寻优的优点结合起来,既避免了遗传算法到达最优解附近随机搜索最优解的缺点又克服了神经网络在权值阈值训练中易陷入局部极小值的缺点。
表2是分别采用改进后算法与原算法得到的神经网络分类错误率。改进后的算法与原算法相比,训练数据与测试数据的分类错误率均较低,说明对本例而言,改进后的算法分类准确率优于原算法。

表2 用改进后算法与原算法分类错误率统计表
3 影响关系分析
平均影响值法(MIV)被认为是在神经网络中评价自变量相关性最好的指标之一,可用于确定神经网络中输入变量对输出变量影响大小,其绝对值大小代表影响的相对重要性。故采用MIV法研究上市公司相关指标对独立机构投资者持股比例的影响关系。MIV法的步骤这里不作介绍,请参阅相关文献。
采用训练好的改进遗传神经网络,并依据上述步骤求解得到各自变量MIV绝对值如表3所示。

表3 自变量MIV绝对值
从表3可得,上市公司的安全性和盈利性对独立机构资者所持上市公司股权比例影响比较大。总体来说独立机构投资者偏好于持有规模大,盈利能力强,且风险小的企业的股票,独立机构投资者持股特征具有追求盈利且规避风险的特性。投资者的投资目标决定了持股行为,独立机构投资者的投资目标是在保证资金安全的基础上追求盈利,这一方面决定了其倾向于选择安全性较高的企业,而规模大、偿债能力强的企业相对来说比较稳定与可靠,另一方面也决定了其倾向于选择盈利性高的企业,因而反映企业业绩的每股收益和净资产收益率也是其在选择投资目标时重点关注的指标。
4 结论
本文研究了独立机构投资者持股行为特征,在研究中为了提高模型精度和计算效率,改进了遗传神经网络方法,改进后的算法较原算法在分类准确率和效率上有一定程度的提升,之后在建模的基础上采用MIV方法研究了影响关系,结果表明上市公司的安全性和盈利性对独立机构资者所持上市公司股权比例影响较大,这体现了独立机构投资者追求盈利且规避风险的特性。
本文的不足之处在于仅采用了2010年一年的数据进行研究,还应进行更大样本的实证研究工作。
[1]Bushee B,Noe C.Corporate Disclosure Practices,Institutional Investors,and Stock Return Volatility[J].Accounting Research,2000,38(S).
[2]Milbourn T T.CEO Reputation and Stock-based Compensation[J].Journal of Financial Economics,2003,68(2).
[3]史峰,王小川,郁磊,李洋.Matlab神经网络30个案例分析[M].北京:北京航空航天大学出版社.2009.
[4]陈明忠.BP神经网络训练算法的分析与比较[J].科技广场,2010,(3).
[5]闫利军,李宗斌,杨晓春.基于混合优化算法的遗传算法参数设定研究[J].系统工程与电子技术,2007,(10).

