弹药无法改装的地炮甲弹射表编拟方法

张宏江， 王智杰， 杜 锋， 孟庆均， 王鹏新

(1. 装甲兵工程学院装备试用与培训大队， 北京 100072； 2. 中国白城兵器试验中心， 吉林 白城 137001)

地炮甲弹射表编拟所需弹药要求从工厂调拨或者对库存弹药进行改装，以精确测量弹丸飞行体质量，并配装摘火引信。而对于近年无生产定购任务而又需编拟射表的弹药，均调拨库存产品。由于大部分甲弹为定装弹，库存弹药无法精确测量其飞行体质量；同时，若为弹底引信，则无法进行摘火操作。为完成此类射表编拟任务，必须对试验方法和数据处理方法进行研究，在保证试验安全的前提下，使所编拟出的射表精度达到最高，并结合该弹药射表精度要求分析此种精度的射表是否满足部队使用要求[1]。

1 对弹丸质量不准确的处理

射表编拟过程中必须采用合理的数据处理方法，使弹丸质量不准确所造成的射表误差降到最小。在射表试验中，将相同弹重等级的弹丸分为一组，并在射表编拟数据处理时，取每一组弹丸质量的中间值(以下称作中间弹重)作为这一组弹丸的质量。同时，为确定使用无法测量飞行体质量的库存弹药所编拟的射表是否可提供部队使用，必须分析以此方法编拟射表的误差大小。

1.1 阻力系数的提取

某型破甲弹射表试验所调拨的弹药为标准级，但是不能精确测量弹丸质量，其中间弹重为表定弹丸质量18 500 g，该弹重等级弹丸的最大质量(以下称作最大弹重)为18 561.7 g。此次射表编拟进行了3组2.5 km立靶试验，分别以试验弹丸的中间弹重和最大弹重处理贝尔雷达测速数据，提取弹丸自身阻力系数C[2-4]。当弹重取中间弹重时，

式中：Ma为飞行马赫数。当弹重取最大弹重时，

提取的阻力系数曲线比较结果如图1 所示。

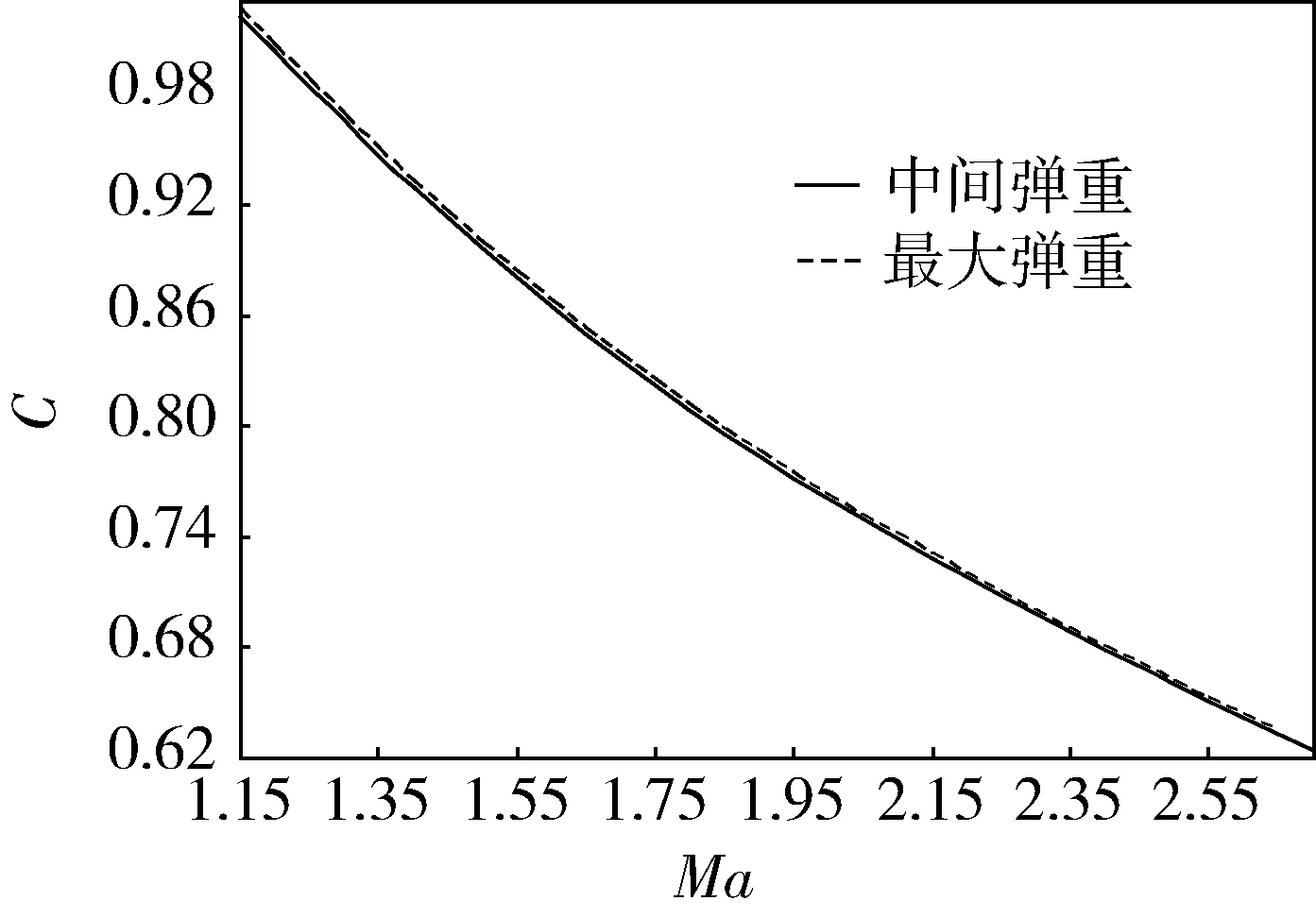
图1 弹丸取不同质量时的阻力系数曲线

1.2 立靶符合

对试验结果进行符合计算是获取射表编拟关键参数的必需环节，其目的是为射表计算确定阻力符合系数。立靶试验符合计算是在实际射击条件下，针对在不同弹丸质量情况下提取的弹丸阻力系数，对2.5 km立靶试验坐标和弹丸飞行时间进行符合计算，符合结果如表1所示，K1、K2分别为以中间弹重和最大弹重进行符合计算的结果。

表1 2.5 km立靶试验阻力符合系数

1.3 误差分析

射表计算是在标准条件下对弹道进行计算，针对已知的2条阻力系数曲线和对应的阻力符合系数，弹道计算结果如表2、3所示。

由表2、3可以看出：利用中间弹重编拟射表会造成一定的误差，而且误差随着射程的增加而增大，对于该型破甲弹，在射角为2°时造成的射程误差会达到1.611‰。

表2 不同弹重条件下的射表计算对比

表3 不同弹重条件下的射程对比

2 对引信无法摘火的处理

对于部分弹底引信的库存弹药，其引信无法进行摘火操作，如果进行立靶试验,就可能造成2种安全隐患：一是弹丸穿过立靶时发生爆炸，损毁立靶和测试设备；二是在试验场区布下大量引信保险已解脱的未爆弹丸，给弹丸销毁造成极大困难，对场区安全造成巨大威胁。为此，必须重新设计试验方案，并对其可能造成的射表误差进行分析。

2.1 试验方法

为增加引信发火率，减轻销毁弹丸的压力，减小对场区安全的威胁，不进行立靶试验，而是取较大射角进行阻力系数试验[5]。试验中，利用初速雷达测试弹丸初速；利用贝尔雷达测试与飞行时间对应的弹道径向速度和斜距；利用机动气象站测试地面气象诸元;根据最大弹道高选择合适的气象测试设备测试低空或高空气象诸元[6-8]。

2.2 阻力系数提取

为获取研究数据，以某型可改装破甲弹射表试验为例，进行了3组2 km立靶试验和3组射角为11°的阻力系数试验。对试验数据进行处理，提取的弹丸自身阻力系数为

其拟合曲线如图2所示。

图2 某型可改装破甲弹阻力系数曲线

2.3 符合计算

在实际射击条件下，利用提取的弹丸自身阻力系数，对2 km立靶试验的坐标和弹丸飞行时间进行符合，得到立靶阻力符合系数；针对2 km立靶试验和11°射角阻力系数试验的雷达数据，在斜距2 km附近取点，对斜距和相应的弹丸飞行时间进行符合计算，得到其斜距阻力符合系数，如表4所示。其中，K3、K4、K5分别为2 km立靶试验立靶阻力符合系数、2 km立靶试验斜距阻力符合系数和11°射角阻力系数试验斜距阻力符合系数。

表4 某型破甲弹阻力符合系数

比较上述符合结果，如果认为对立靶坐标和飞行时间的符合是精确值，那么对2 km立靶试验符合所得斜距阻力符合系数误差为2.891‰ ，11°射角阻力系数试验的斜距阻力符合系数误差为7.321‰ 。

2.4 误差分析

在标准条件下进行弹道计算[9]，其结果如表5、6所示。

表5 不同阻力符合系数下的射表计算对比

表6 不同阻力符合系数下的射程对比

由表5可以看出:对于该型破甲弹，用2 km立靶试验射击数据进行射表编拟时，如果认为立靶坐标和飞行时间的测量结果是精确值，那么利用贝尔雷达所测斜距和飞行时间编拟射表所造成的误差会随着射程的增加而增大。但实际上对立靶坐标的符合结果并不是精确值，两者之间的误差并不完全是由斜距符合所造成，其中包括了大量的试验误差，如立靶距离的测量误差、立靶坐标的测量误差、立靶不垂直地面造成的误差、立靶靶面与射击线不垂直造成的误差、飞行时间的测量误差、各点位坐标的测量误差、雷达斜距的测量误差等。所以实际上利用贝尔雷达所测斜距和飞行时间编拟射表所造成的误差可能小于表5中所列结果。在地炮甲弹射表编拟中规定，立靶距离测量精度不小于1/5 000，而贝尔雷达距离测量随机误差仅为0.1 m ，所以对于标校过

的雷达,其精度应该是满足要求的。

由表6可以看出:如果用较大射角阻力系数试验代替立靶试验进行射表编拟，对该型破甲弹射表所造成的误差也是随着射程的增加而增大，在射角为0.5°时，射程误差为1.449‰，而在射角为2°时，射程误差为3.533‰。当然这种误差中2次试验的误差应该占很大部分，在误差分析中应当以2 km立靶试验为主。

3 结论

对于无法精确测量弹丸飞行体质量的情况，取每一组弹丸弹重等级的中间值作为这一组弹丸的质量，并对可能造成的最大误差进行分析，利用该分析结果与该弹药射表精度要求进行对比，可以确定是否可利用该无法改装弹药编拟射表；

2) 对于引信无法摘火的甲弹，不进行立靶试验，而是取较大射角进行阻力系数试验，利用标校过的雷达提供弹道速度、飞行时间和斜距编拟射表，该方法解决了目前该类弹药无法进行射表编拟的难题。

参考文献：

[1] 王燕生. 提高射表精度和射表使用精度的几个建议[J]. 弹道学报，1997，9(2)：95-96.

[2] Qi Z K. Multi-spline Technique for the Extraction of Drag Coefficients from Radar Data[J]. Journal of Beijing Institute of Technology, 1994, 3(1): 33-42.

[3] 宋锦武，祁载康，林德福，等. 对比试验法在射表编制中的应用研究[J]. 弹道学报，2003，15(4)：22-26.

[4] 朱宁，林德福，徐劲祥. 弹丸阻力系数辨识模型[J]. 兵工自动化，2005，24(4)：18-21.

[5] 林德福，祁载康. 非常规炮弹阻力系数与攻角辨识方法研究[J]. 系统仿真学报，2006，18(S2)：282-284.

[6] 陈群斋. 一种快速高精度的射表数据处理方法[J].火力与指挥控制，1995，20(3)：24-27.

[7] 徐劲祥，祁载康，林德福，等. 火箭炮射表编拟及发射诸元快速装定研究[J]. 南京理工大学学报，2004，28(3)：333-336.

[8] 崔新军. 榴弹射表编拟中最佳符合射角的确定及射表精度对比[J]. 火控发射与控制学报，1996，8(1)：60-66.

[9] 何友，闫红星. 火炮射表数据处理方法评述[J]. 火力与指挥控制，1994，19(3)：45-49.