基于蒙特卡罗的复杂可修系统预防性维修周期决策
杨 智, 黄学卫, 黄松华
(镇江船艇学院维修教研室, 江苏 镇江 212003)
当前对零部件预防性维修周期的决策研究主要从2方面进行:一是理论研究,假定其寿命服从特定分布,给定平均修复时间和平均预防性维修时间,以可用度最大或者单位工作时间总费用最小为目标,确定最佳的维修周期[1-4];二是基于蒙特卡罗的仿真研究,由于零部件寿命、修复时间和预防性维修时间可以服从任意分布,从而避免了常规数学建模的大量理论计算,突破了理论分析的局限性[5-6]。
对于复杂的可修系统,由于零部件寿命和修复时间分布任意,使得建模和仿真困难。传统方法是分别确定系统中不同零部件的预防性维修周期,然后综合权衡确定系统的维修周期[1]。但该方法割裂了系统中零部件之间以及零部件与系统之间的联系。对于建立复杂可修系统中零部件之间联系的问题,Dekker等[7-9]认为将系统分解为多个部件时,是视为多个独立的单部件决策问题还是整体的多部件决策问题,取决于部件之间的维修相关性。蔡景等[10-11]从维修经济相关性的角度,提出了将预防性维修和故障维修有机结合的思路,在此基础上,又建立了以系统预防性维修费用率最小化为目标的优化模型,但此方法忽视了零部件与系统之间的联系,不能系统、直观地描述系统中故障传递的过程。故障树分析法(Fault Tree Analysis,FTA)通过分析可能造成复杂系统故障的各种因素,显示复杂系统各级故障之间的传播关系[2-3]。目前,已有研究者利用FTA对复杂系统可靠性进行仿真分析[12-14],但很少将其与预防性维修周期决策相结合。为此,笔者利用FTA建立了复杂系统故障树模型,提出了基于蒙特卡罗方法,以可用度最大为目标确定系统最优预防性维修周期,进而改进系统设计的思路。
1 仿真原理
1.1 系统组成
设系统S由n个部件组成,Zi(i=1,2,…,n)为系统的组成部件。应用FTA建立系统的故障树模型,顶事件为系统S的故障事件,底事件为部件Zi的故障事件,即系统有1个顶事件和n个底事件。
1.2 仿真模型
设部件Zi的故障分布函数为Fi(t),维修时间分布函数为Mi(t)。假设部件发生故障后不能马上被发现,直到系统发生故障,或者达到预先给定的预防性维修周期T(T仅为工作时间,不包含故障检测和修复时间)之后,才能通过检测发现(因其为复杂系统,所以不管是事后维修还是预防性维修,均需经过检测才能对故障部件定位),系统每一次的检测时间为常量Tf。当系统发生故障时间小于T时,对发生故障的部件进行事后维修,其他部件处于停止工作状态;当系统发生故障时间大于等于T时,对系统进行预防性维修,系统预防性维修时间分布函数为Mp(t)。假定事后维修和预防性维修都是完全维修,系统修复如新。仿真过程可分5个步骤。
1) 设定仿真次数N,利用通扫故障树法[5]得到系统的故障发生时间及发生故障的部件。通过蒙特卡罗法,对n个部件进行随机抽样,得到各部件的故障时间ti=F-1(η),η为随机数。将n个故障时间由小到大排序为t1′,t2′,…,tn′,相应的部件顺序为Z1′,Z2′,…,Zn′。首先将Z1′置于故障状态,其余部件在此时均未发生故障,利用故障树结构函数或系统故障的最小割集底事件来判断系统S是否发生故障。若系统发生故障,则其发生故障时间为t1′;若系统未发生故障,则推进到下一个部件故障时间t2′,此时Z1′、Z2′已发生故障,再次判断系统此时S是否发生故障。若系统发生故障,则系统发生故障时间为t2′;若系统未发生故障,则推进到下一个部件故障时间t3′。依次最终找到系统发生故障时间t及发生故障的m个部件。
2) 分别计算系统发生故障后总的修复时间及预防性维修时间。对m个故障部件进行随机抽样,得到各故障部件的维修时间twj=M-1(η)。设每项维修作业之间相互独立,且只有一个维修单元,根据串行作业模型[2],系统总的修复时间为
(1)
预防性维修时间可直接产生,即
(2)
3) 重复步骤1)、2),直到达到规定的仿真次数N,计算可用度[2],即
A=U/(U+D),
(3)
式中:A为可用度;U为工作时间;D为停用时间。根据U的计算方法不同,可用度计算可分为2种情况[2]:一是工龄维修,即产品在使用中即使未发生故障,到了规定的维修工龄,也要进行预防性维修,如未到规定工龄发生故障,则进行修复性维修;二是定时维修,即每隔预定的维修间隔,对使用中的产品进行预防性维修,即使产品在此间隔期内发生过多次故障且维修过,到达维修间隔时间时也一起维修。
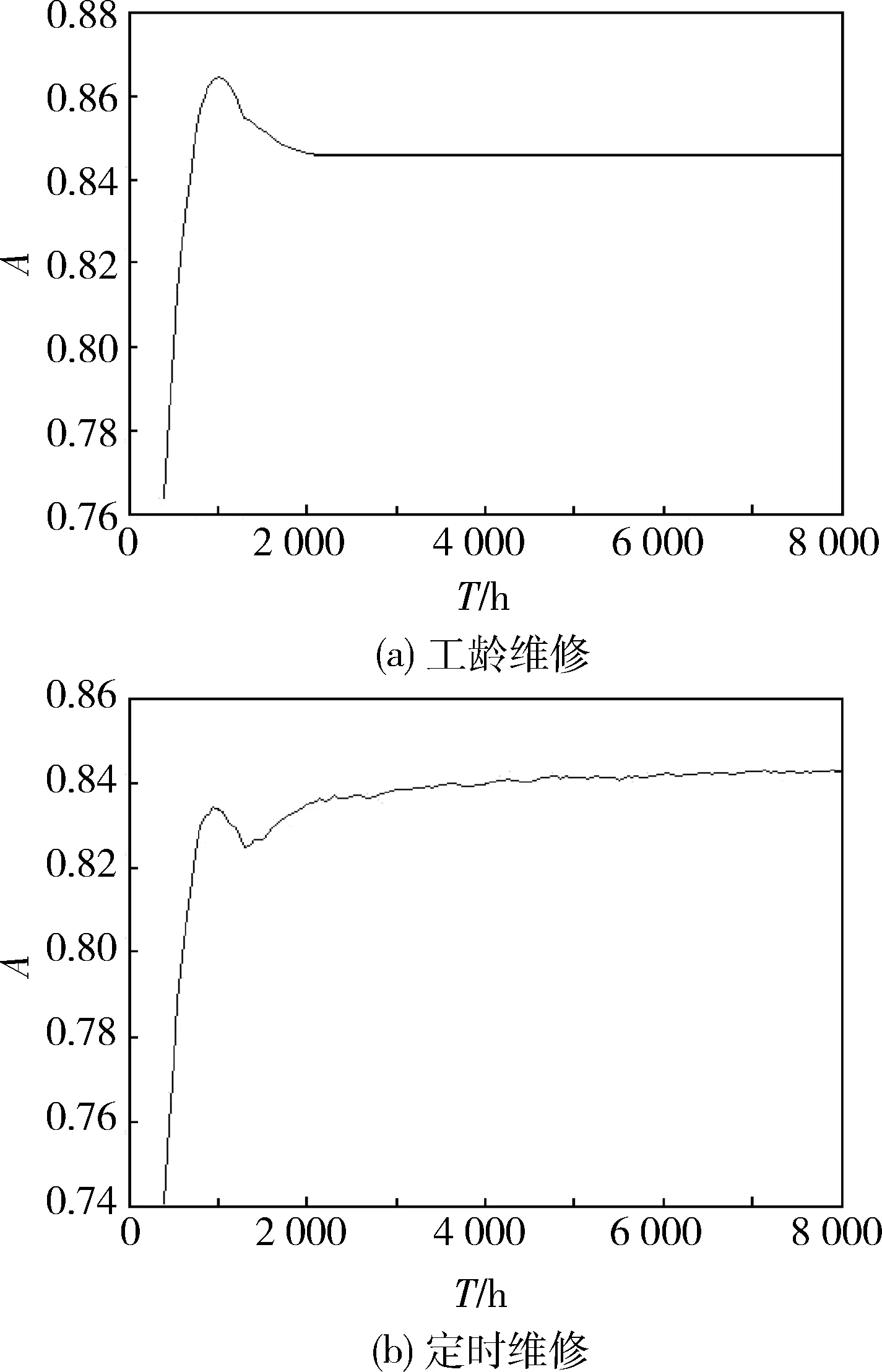
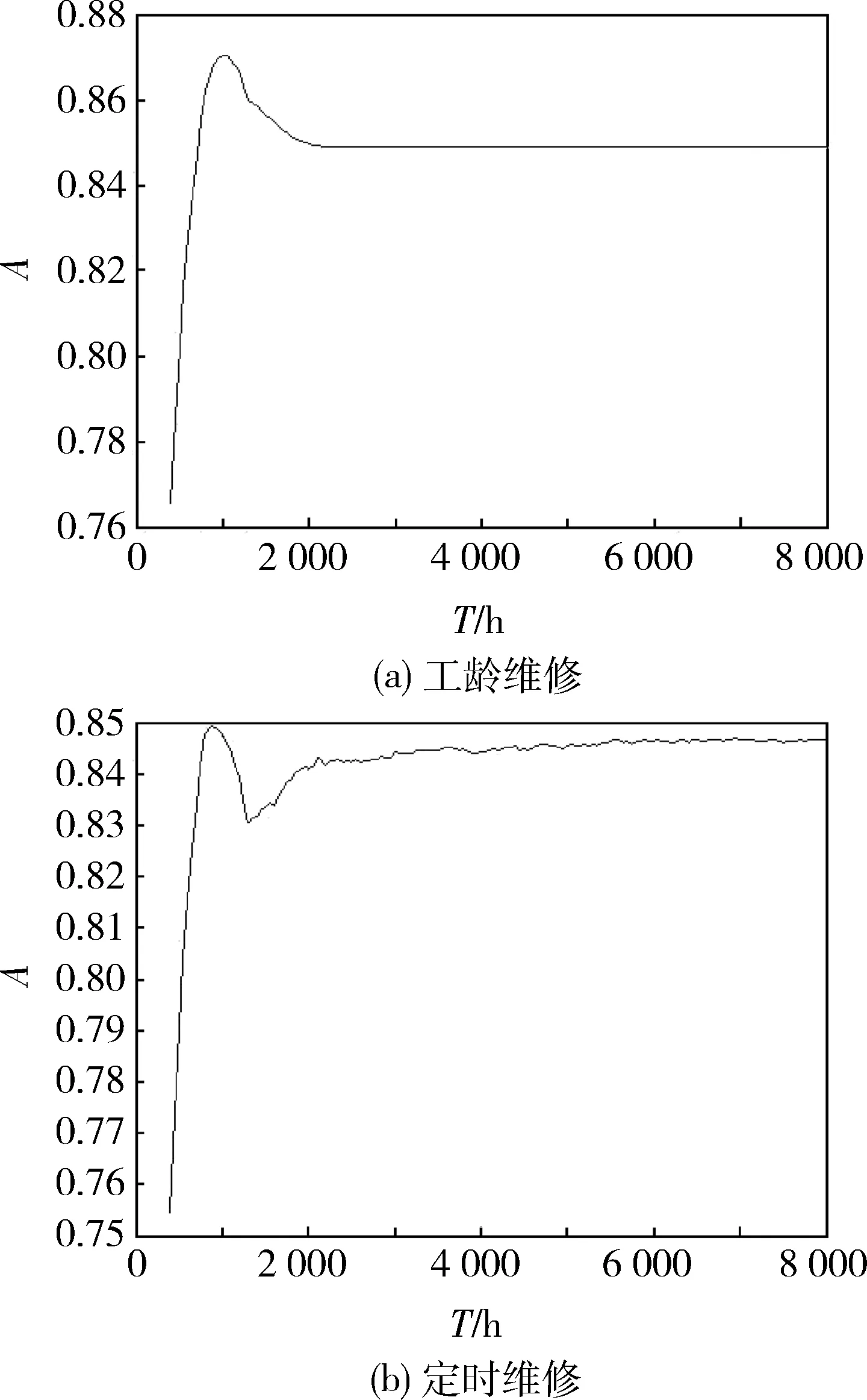
(1)采用工龄维修时,比较某次仿真中系统发生故障时间t与给定的预防性维修周期T。若t (4) (5) 式中:M为N次仿真中t (2)采用定时维修时,首先通过累计工作时间确定在第k次仿真中的一个周期T内系统发生故障的次数H,令 式中:ti为第k次仿真中第i次系统发生故障的时间。当tH 式中:twp为每一次系统故障的修复时间,p=1,2,…,H,可由式(1)得出。所以有 U=NT, (6) (7) 式中:tywk为第k次仿真中系统总的预防性维修时间,可由式(2)得出,1≤k≤N,k∈N。将式(6)、(7)代入式(3)可得 4) 改变T值,按上述步骤进行仿真,找出最大可用度对应的T值,即为最佳预防性维修周期。 5) 改变系统参数或系统中关键零部件(可通过系统故障树的最小割集确定)的参数(如故障分布函数、维修时间分布函数等或这些函数中的某些参数),对提高系统可用度,改进系统设计进行探索。 某装备系统由5个部件组成,故障树模型由门事件(A、B、C、D、E)、底事件(X1、X2、X3、X4、X5,分别表示相应的部件故障)和顶事件(M,表示系统故障)组成,如图1所示。各部件故障分布函数F(t) 图1 某装备系统故障树模型 和维修时间分布函数M(t)如表1所示。 系统预防性维修时间分布Mp(t)为指数分布,平均预防性维修时间1/λ=120 h,系统单次检测花费的时间为3 h。 表1 各部件故障、维修时间分布类型与参数 根据仿真原理,通过Matlab编程计算可用度。当采用工龄维修时,预防性维修周期T与可用度A的关系如图2(a)所示;当采用定时维修时,预防性维修周期T与可用度A的关系如图2(b)所示。 图2 预防性维修周期与可用度的关系 由图2可见:对于工龄维修,T=1 000 h时,A取得最大值0.864;对于定时维修,T>5 000 h时,A取得最大值0.842,且基本保持恒定。从系统可用度的角度考虑,应采取工龄维修模式,预防性维修周期取1 000 h。 考察图1中系统的最小割集,可知X1对应的部件Z1因阶数最低而最重要,为此,对Z1进行技术改造,假定将其工作寿命提高一倍,达到1/λ=3 400 h,其他参数维持不变。可得2种维修模式下,预防性维修周期与可用度的关系,如图3所示。 图3 系统改进后预防性维修周期与可用度的关系 由图3可见:对于工龄维修,T=1 000 h时,A取得最大值0.87;对于定时维修,T=900 h时,A取得最大值0.849。可用度比改进前均提高约0.006,且仍是工龄维修占优。从系统可用度的角度考虑,仍应采取工龄维修模式,预防性维修周期取1 000 h,与改进前相同。 本文对复杂可修系统的预防性维修周期决策进行了探讨,建立了以可用度最大为目标的工龄维修和定时维修2种模式下的仿真分析模型。与传统方法相比,建立了零部件与系统之间的联系,反映了故障传递的过程。进一步的研究可从以下2方面进行: 1)本文设定当系统发生故障后通过检测发现故障部件,并依次对其进行维修,没有考虑维修的顺序,然而在紧急场合,要求系统停工时间越短越好,此时就需首先对重点部件进行维修,在系统恢复工作之后,再对系统中不重要部件进行维修,下一步应考虑维修的有序性问题; 2) 本文假定系统经维修后修复如新,而在有些情况下,这一点并不能成立,即只能达到基本修复,下一步应考虑此种情况。 参考文献: [1] 陈学楚. 现代维修理论[M]. 北京:国防工业出版社,2003:126-150. [2] 甘茂治,康建设,高崎. 军用装备维修工程学[M]. 北京:国防工业出版社,2001: 244-250. [3] 宋保维. 系统可靠性设计与分析[M]. 西安:西北工业大学出版社,2008:84-87. [4] 贾希胜. 以可靠性为中心的维修决策模型[M]. 北京:国防工业出版社,2007:71-99. [5] 杨为民,盛一兴. 系统可靠性数字仿真[M]. 北京:北京航空航天大学出版社,1990:336-394. [6] 肖钢,李天柁. 系统可靠性分析中的蒙特卡罗方法[M]. 北京:科学出版社,2003:153-157. [7] Dekker R, Van der Duyn Schouten F A, Wildeman R E. A Review of Multi-component Maintenance Models with Economic Dependence[J]. Mathematical Methods of Operations Research, 1997, 45(3): 411-435. [8] Dekker R, Roelvink I F K. Marginal Cost Criteria for Preventive Replacement of a Group of Components [J]. European Journal of Operational Research, 1995, 84(2): 467-480. [9] Archibald T W, Dekker R. Modified Block-replacement for Multiple-component Systems [J]. IEEE Transactions on Reliability, 1996, 45(1): 75-83. [10] 蔡景,左洪福,王华伟. 多部件系统的预防性维修优化模型研究[J]. 系统工程理论与实践,2007(2):133-138. [11] 蔡景,左洪福,王华伟. 基于经济相关性的复杂系统维修优化模型研究[J]. 系统工程与电子技术,2007,29(5):835-838. [12] 张玉涛,唐俊,张明清,等. 基于蒙特·卡罗方法的可靠性仿真过程模型研究[J].系统工程与电子技术,2008,30(7):1374-1385. [13] 吕学志,于永利,陈立勇,等. 基于Simulink的复杂可修系统的建模与仿真方法[J]. 装甲兵工程学院学报,2009,23(4):15-20. [14] 袁静,胡昌华,徐瑞,等. 一类改进故障树分析法的可靠性仿真及应用[J]. 计算机应用研究,2006(11):167-172.2 应用实例
2.1 系统参数设定
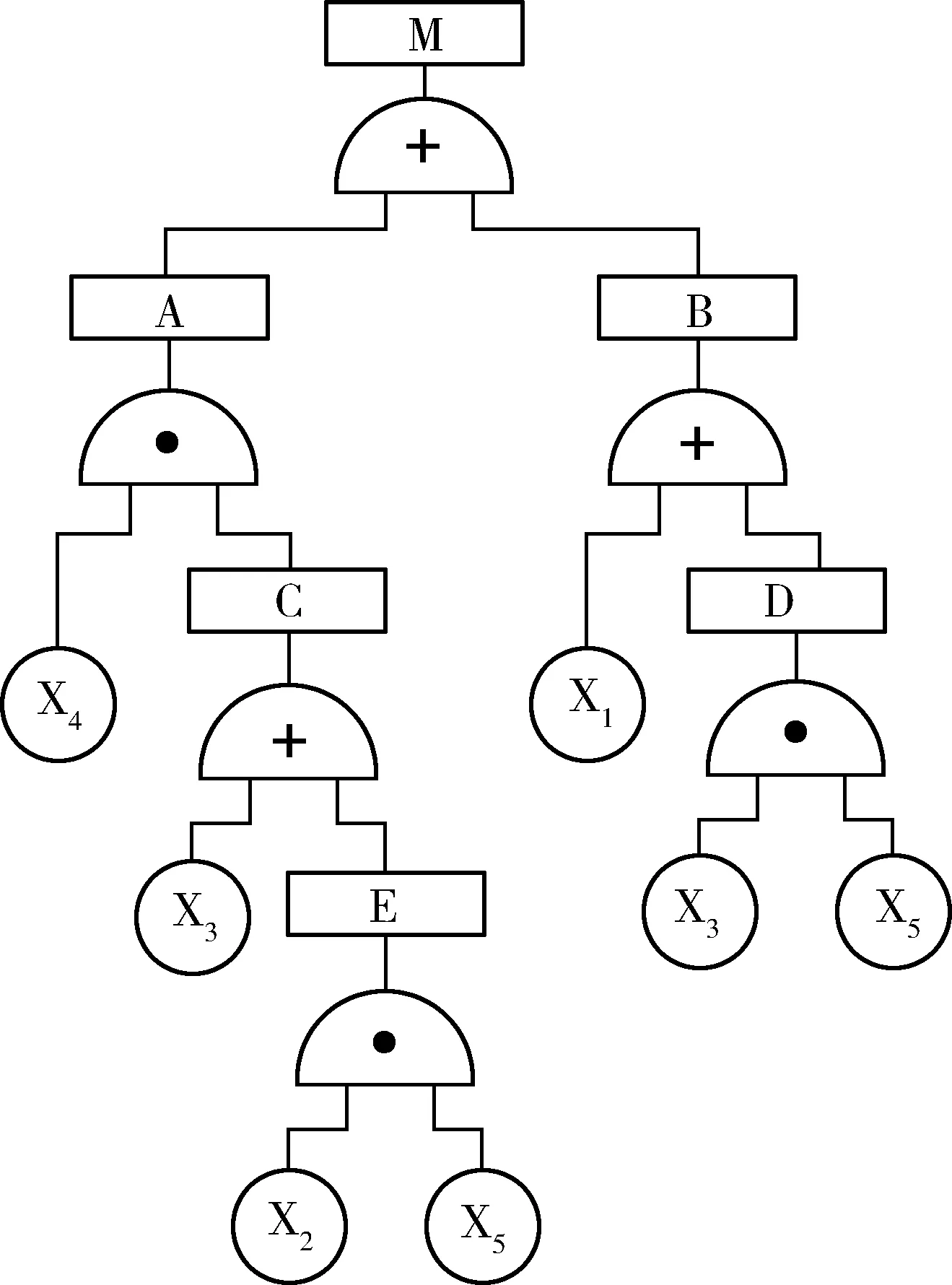
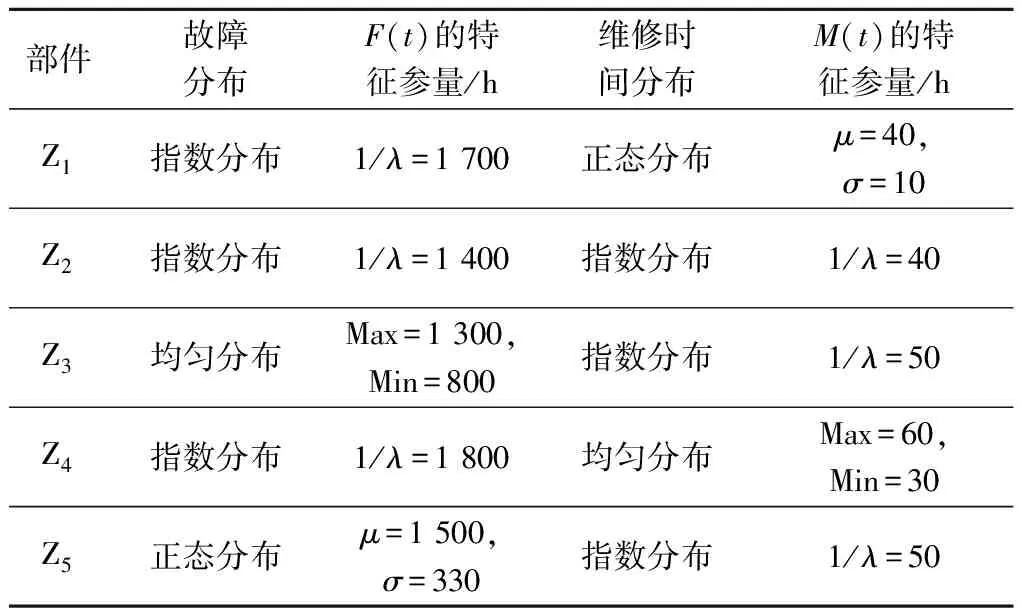
2.2 仿真结果
2.3 系统改进
3 结论

