基于改进的可拓层次分析法的指挥控制系统作战效能评估指标赋权

郑慧娟

(南京陆军指挥学院作战实验中心， 江苏 南京 210045)

指挥控制系统是保障指挥员和指挥机关对作战人员和武器系统实施指挥和控制的信息系统，是指挥信息系统的核心。指挥控制系统作战效能指的是指挥控制系统在执行作战任务时所体现出来的使用价值，是系统在作战人员使用下，通过发挥其作战能力和作战适应性执行作战任务达到预期目标的程度[1]。指挥控制系统作战效能评估一般要经过4个阶段：建立指标体系；确定指标权重；度量末级指标；指标聚合计算。其中，确定指标权重(指标赋权)是效能评估的关键环节之一，指标赋权的合理性直接决定着指挥控制系统作战效能评估结果的可信度。

层次分析法(Analytic Hierarchy Process，AHP)是指标赋权的常用方法，但AHP在实际应用中存在着一定的局限性，主要表现在：专家的判断容易发生偏差；对于人的判断思维的模糊性无法表达；判断矩阵需要进行一致性检验，当未通过检验时，其计算结果的可信度将会受到影响[2]。为此，笔者引入了专家群体决策和可拓学理论，在提高和完善层次分析法的基础上，提出了一种改进的可拓层次分析法(Extension Analytic Hierarchy Process, EAHP)，并将其应用于指挥控制系统作战效能评估指标权重的确定。

1 指标体系的建立

影响指挥控制系统作战效能的因素具有数量多、范围广、联系复杂等特点，在指标的选取和体系的建立过程中，必须深刻理解系统功能及其作战应用，才能获得系统、完整、科学的指标体系，为作战效能评估提供可信的初始信息。根据指挥控制系统功能体系结构以及作战效能定义可知，影响作战效能的因素主要来自于3个方面：一是作战能力，其大小直接体现了系统对整个作战体系提供支持的范围和强度，是影响作战效能的主体指标；二是作战适应性，交战过程中受战场环境、敌我对抗等因素影响，系统的固有能力并不能完全释放，因此指挥控制系统必须对战场等外部环境具有一定的适应能力，以确保最大限度地实现系统的技战术功能；三是人员素质，有效的指挥与控制首先来源于经过良好训练的合格人员，因此必须重视人员素质对指挥控制系统作战效能的影响。在评估指挥控制系统作战效能的实践中，三者缺一不可，相互促进，共同决定了指挥控制系统作战效能的高低。由此建立的指挥控制系统作战效能评估指标体系如图1所示[3]。

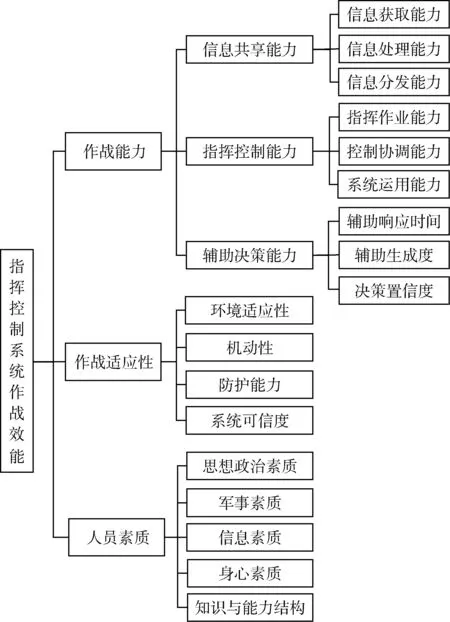
图1 指挥控制系统作战效能评估指标体系

2 EAHP赋权方法

在传统的多属性群决策模型中，确定专家权重的方法是将专家权重作为一个独立问题，建立评估专家的因素集合，产生专家权重。由于专家的个人经历、知识结构、文化背景及相关学术领域均不尽相同，因此对于不同的问题，专家的权重系数应当是不同的。另外，由于个体偏好，即使是面对专家精通的问题，其所作判断也可能不准确[4]。而通过对专家提供的信息(判断矩阵)进行分析来确定专家权重，既可以有效地避免个体差异，又体现了模型的贯通性。传统的可拓AHP方法是以2个可拓区间数a≥b的可能性程度作为赋权依据[5]，因此在a与b的重要性趋于一致时所得出的结论并不可信。EAHP赋权方法则选择多名专家进行调查，根据其给定的判断矩阵确定专家权重，并以评估指标的重要性程度确定其权重系数[6-10]。

2.1 构造可拓判断矩阵

聘请若干专家将指标体系第r-1层的某一个指标或准则，同第r层与之有关的全部指标两两比较，利用可拓区间数表示其相对重要程度，从而构造出一个可拓判断矩阵A=[aij]n×n，其元素aij=是一个可拓区间数，可拓判断矩阵为正互反矩阵，即

aii=1，

2.2 确定专家权重

参与确定指标权重系数的专家有多位，并且专家的相对权重也有所差别，确定专家权重的步骤如下。

(1)

由此得到专家群体可拓判断矩阵为

A*=A-*,A+*

(2)

(3)

根据专家判断的一致性原则，Δθt越小，表明第t位专家的判断与专家群体判断的相似度越高，应赋予更高的权重。

3) 计算专家权重。用ρt表示第t位专家的权重，则

(4)

将ρt进行归一化处理，可得第t位专家的权重系数，即

(5)

2.3 计算综合可拓判断矩阵

(6)

可得综合可拓判断矩阵为

2.4 确定指标权重

当确定了综合可拓判断矩阵后，为确定第r层指标相对于第r-1层某指标或准则的相对权重，还需进行如下计算：

2) 计算系数k、m，即

(7)

(8)

3)求取权重向量，即

S=[kx-，mx+]=(S1，S2，…，Sn)T；

(9)

4) 计算各指标的权重，用Pi表示第r层上第i个指标相对于第r-1层某指标或准则的相对权重，则

(10)

经归一化处理后，可得第r层上各指标相对于第r-1层某指标或准则的权重向量P=(P1，P2，…，Pn)T。若第r-1层有m个指标或准则，则权重向量为一个n×m的矩阵，即

若第r-1层各指标或准则对总目标的排序权重向量为Q=(q1，q2，…，qm)T，则第r层上各指标对总目标的综合权重为W=PQ=(w1,w2,…,wn)T。

3 应用举例

在图1所示的指挥控制系统作战效能评估指标体系中，选取指挥控制系统作战效能的一级指标(作战能力、作战适应性、人员素质)作为研究对象，并将这3个指标抽象为U1、U2、U3。选取4位专家组成评价小组参与这组指标的权重确定，并根据上述EAHP赋权方法对指标进行赋权。

1)构造可拓判断矩阵。在一定的作战任务背景下，以问卷调查等形式，根据作战能力U1、作战适应性U2和人员素质U3对作战效能影响的重要程度，由4位专家对U1、U2、U3进行两两比较，并分别给出了相应的可拓区间数判断矩阵，即

A*=

3) 计算综合可拓判断矩阵。根据式(6)以及已经求得的专家权重系数，可得集结后的综合可拓判断矩阵，即

分解后，可得

x-=(0.488 2,0.323 5,0.188 3)T，

x+=(0.479 8,0.331 7,0.188 5)T，

根据式(7)-(10)，可得k=0.970 6，m=1.024 8，S1=0.473 8，0.491 7，S2=0.314，0.339 9，S3=0.182 8，0.193 2，P1=0.485，P2=0.327，

P3=0.188。从而得到归一化权重向量P=(0.485，0.327，0.188)T，即指标“作战能力U1”、“作战适应性U2”和“人员素质U3”相对于作战效能的权重分配为wU1=0.485,wU2=0.327,wU3=0.188。

4 结论

本文结合专家群体决策和可拓学理论，研究了一种EAHP赋权方法。根据专家提供的信息动态地确定专家权重，既有效地避免了个体差异，又充分发挥了多位专家共同决策的特点，并且以评估指标的重要性程度确定其权重，弥补了传统可拓层次分析法在指标重要性程度相近时计算结果不可信的缺陷。从理论上说，EAHP方法更为完善，评估计算结果更为合理。将此方法应用于指挥控制系统作战效能评估指标的权重计算，增加了评估结果的可信性。

参考文献：

[1] 罗兴柏，刘国庆．陆军武器系统作战效能分析[M]．北京：国防工业出版社，2007：6．

[2] 孔令明， 王云峰．基于可拓层次分析法的物流中心选址评价[J]．技术经济与管理研究，2009(9)：25-27．

[3] 汪彦明，徐培德．ANP的指挥控制系统作战效能评估[J]．火力与指挥控制，2007，32(11)：77-78．

[4] 李琳，刘雅奇，李双刚．一种群决策专家客观权重确定的改进方法[J]．运筹与管理，2011，20(4)：77-78．

[5] 高洁，盛昭瀚．可拓层次分析法研究[J]．系统工程，2002，20(5)：6-11．

[6] 蔡文，杨春燕，林伟初．可拓工程方法[M]．北京：科学出版社，1997：177-179．

[7] 陈晓红，刘益凡．基于区间数群决策矩阵的专家权重确定方法及其算法实现[J]．系统工程与电子技术，2010，32(10)：2128-2131．

[8] 聂静涛，徐枞巍．群体多属性决策方法及其应用[J]．南京航空航天大学学报，2006，38(4)：524-528．

[9] 寿志勤，陶建平，周健，等．基于可拓层次分析法的校园网络安全评估指标体系研究[J]．合肥工业大学学报：自然科学版，2010，33(11)：1643-1647．

[10] 王念秦，罗东海．滑坡发育阶段判定的改进可拓层次分析方法[J]．中国地质灾害与防治学报，2008，19(4)：27-31．