平头弹丸侵彻B4C陶瓷/金属复合靶板的数值模拟

孙炜海， 鞠桂玲， 杨班权

(1. 装甲兵工程学院机械工程系， 北京 100072； 2. 装甲兵工程学院基础部， 北京 100072)

陶瓷材料具有密度低、弹性模量大、压缩强度高以及硬度大、熔点高等优良性能，在坦克和装甲车辆、直升飞机及舰船的防护结构中具有广泛的应用。由于陶瓷为典型的脆性材料，容易发生拉伸断裂，因此经常与塑性金属材料组成复合装甲。目前，陶瓷/金属复合装甲正朝着应用更广泛、制造和安装更方便、结构更轻质的方向发展。在所有抗弹陶瓷中，碳化硼(B4C)陶瓷硬度最大而密度最小，因此其在防护领域具有广阔的应用前景[1]。

M.L. Wilkins[2]通过试验方法研究了陶瓷/金属复合靶板的抗弹性能，给出了大量试验数据。C.E.Anderson等[3]研究了7.62 mm APM2弹侵彻B4C陶瓷/铝合金复合靶板的过程。G.R.Johnson等[4]研究了B4C陶瓷的动态力学性能及B4C陶瓷/金属复合靶板在动能弹丸撞击下的侵彻和贯穿行为。傅苏黎[5]、丁华东[6]等通过试验方法研究了碳化硼基双复合装甲板的抗弹性能。应用有限元数值计算方法研究弹丸侵彻靶板问题，不仅有利于对侵彻机理的理解，而且与穿甲试验方法相比，该方法经济、安全、有效，在考虑多因素时优势显著。笔者应用动力学分析通用有限元软件LS-DYNA对平头弹丸垂直侵彻B4C陶瓷/金属复合靶板进行了数值模拟，分析了陶瓷/金属复合靶板的破坏机理，实现了侵彻过程的可视化，并对陶瓷/金属复合靶板的界面连接方式和厚度比对复合靶板防护性能的影响进行了研究，从而为弹靶的设计与优化提供技术支持。

1 计算模型

1.1 有限元模型

平头弹丸的直径为7.6 mm，长度为24 mm，材料为高强度钢，质量为8.32 g。复合靶板由B4C陶瓷面板与6061-T6铝合金背板组合而成，靶板的直径为100 mm，边界固定。

根据平头弹丸垂直侵彻陶瓷/金属复合靶板的对称性，利用LS-DYNA建立轴对称有限元模型，弹丸和靶板均采用四节点板壳单元进行网格划分，单元采用单点积分和沙漏控制，网格尺寸为0.2 mm × 0.2 mm。图1为平头弹丸侵彻由7.2 mm陶瓷面板和6.4 mm金属背板组成的复合靶板的有限元模型。

图1 平头弹丸侵彻复合靶板的有限元模型

弹丸、2层靶板之间的接触均使用CONTACT_2D_AUTOMATIC_SINGLE_SURFACE类型，忽略摩擦，建模采用m-kg-s国际标准单位制。弹丸划分的单元数为2 280，根据靶板厚度不同，靶板划分的单元数从16 250到17 500不等。

1.2 本构方程及材料参数

高强度钢和铝合金均为金属材料，采用Johnson-Cook热粘塑性材料本构方程[7]，该方程包含动态变形过程中材料的塑性硬化、应变率强化和温度软化效应。材料在大应变情况下的流动应力表示为

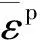
材料的失效与三轴应力、应变率和温度有关，失效应变表示为

计算所用的材料参数见表1，高强钢的参数取自文献[3, 8]，铝合金的参数取自文献[8-9]。表1中:E、G、ν、ρ0、Cp分别为材料的弹性模量、剪切模量、泊松比、密度和比热容；C0、S1、γ0、a为状态方程中的常数。

表1 高强钢、铝合金的材料参数

陶瓷材料采用JH-2材料本构方程[10]，该方程主要包括对材料的强度、压力和损伤的变化关系的描述。一般陶瓷材料在达到破坏强度之前，可以按弹性材料考虑，而对于发生破坏的陶瓷材料，可以将其视为强度随损伤累积变化的完整材料。

陶瓷材料的强度包括无损伤材料的强度和完全损伤材料的强度2种，根据损伤的变化可以将含损伤陶瓷材料的等效应力表示为

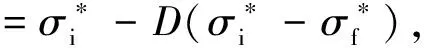
归一化的无损伤材料(D= 0)的等效强度可表示为

归一化的完全损伤材料(D= 1)的等效强度可表示为

表2 B4C陶瓷的材料参数

2 仿真结果及其分析

2.1 数值模拟结果与试验数据的比较

试验数据取自文献[2]，为7.62 mm平头弹丸垂直侵彻7.24 mm B4C陶瓷面板和 6.35 mm铝合金背板胶粘组成的复合靶板，试验测得复合靶板的弹道极限为705 m/s。图2为7.6 mm平头弹丸垂直侵彻7.2 mm B4C陶瓷面板和6.4 mm铝合金背板组成的复合靶板(面密度为35.38 kg/m2)后残余速度的数值模拟结果，通过拟合给出了残余速度随入射速度的变化曲线，考察了2种不同的陶瓷与金属的界面连接情况。

图2 弹丸的残余速度随入射速度的变化曲线

由图2可见：面板和背板采用自由接触时，复合靶板的弹道极限为697.5 m/s；采用固连接触时，其弹道极限为707.5 m/s。由此可见：试验测得数据位于数值模拟得到的2个结果之间，说明数值模拟结果是合理可信的，而且误差较小。为了进行对比分析，本文的有限元计算模型中面板和背板之间分别采用自由接触和固连接触。

2.2 复合靶板的抗弹性能对比分析

为分析复合靶板不同厚度配置对其抗弹性能的影响，分别保持B4C陶瓷/铝合金复合靶板的总厚度13.6 mm和面密度35.38 kg/m2不变，改变陶瓷面板的厚度H1和金属背板的厚度H2，考察复合靶板的抗弹性能。通过数值模拟，给出了2种情况下复合靶板的弹道极限随着H1与复合靶板总厚度H0之比H1/H0的变化曲线，如图3所示，每种情况包含自由接触和固连接触2种接触方式。从图3中可以看出：1)在等厚度和等面密度2种情况下，采用固连接触计算得出的弹道极限总体上比采用自由接触计算得出的结果要大，说明增强对陶瓷面板的约束可以提高复合靶板的抗弹能力；2)2种情况下复合靶板的弹道极限曲线变化趋势比较接近，这是由于B4C陶瓷面板的密度与铝合金背板的密度相差较小；3)复合靶板的弹道极限随着陶瓷面板厚度的增加先增加后减小，这是由于增加陶瓷面板的厚度会增加陶瓷对弹丸的磨蚀，但会减小金属背板对陶瓷面板的支撑作用，因此存在一个最佳的匹配，H1/H0最佳匹配值约为0.72(此时H1/H2≈ 2.6)。但等厚度时，H1/H0在0.63～0.8范围内，等面密度时，H1/H0在0.59～0.88范围内，复合靶板的弹道极限相差小于2.6%，因此B4C陶瓷/铝合金复合靶板的厚度比H1/H0较优范围为：等厚度时，可取为0.63～0.8(H1/H2为1.7～4.2)；等面密度时，可取为0.59～0.88(H1/H2为1.4～7.7)。该范围比文献[12]中给出的Al2O3陶瓷/铝合金复合靶板的厚度比H1/H0较优范围0.5～0.67要大。

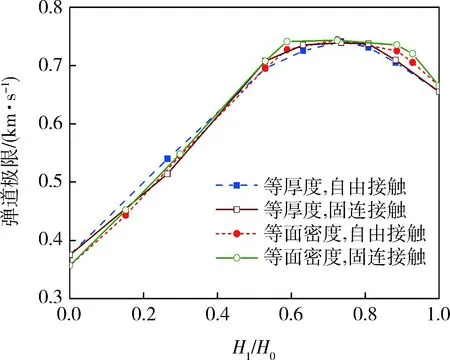
图3 2种情况下采用不同接触方式的弹道极限模拟结果

2.3 侵彻过程分析

图4给出了入射速度为745 m/s的平头弹丸侵彻10 mm B4C陶瓷/3.6 mm铝合金自由接触组成的复合靶板过程中不同时刻的等效应变云图。从图4可以看出：当弹丸撞击复合靶板时，弹靶接触界面周围的陶瓷材料发生碎裂，弹丸发生明显的质量侵蚀，当压缩波到达陶瓷面板背面时反射产生拉伸波，在陶瓷面板的背面产生拉伸裂纹并逐渐扩展，最终演化为陶瓷破碎锥；随后，弹丸加速陶瓷锥一起冲击背板，铝合金背板出现明显的鼓包变形；最后，弹丸和陶瓷碎渣贯穿靶板，背板出现冲塞破坏。数值仿真较好地模拟出了陶瓷/金属复合靶板受弹丸撞击时容易形成的陶瓷锥现象，侵彻过程中陶瓷的断裂破碎、弹丸的侵蚀、铝合金背板的层裂和鼓包变形非常明显，这些都是消耗入射弹丸动能的重要因素。

图4 复合靶板的等效应变云图

3 结论

1) 陶瓷面板和金属背板的连接状态对靶板抗弹能力有明显影响。界面完全固连与自由接触相比，靶板的抗弹能力有明显提高。但在陶瓷面板厚度较小时(H1/H0<0.35)，界面自由接触得出的靶板弹道极限反而更高，分析认为此时金属背板的塑性大变形耗能起重要作用，值得进一步深入研究。

2) 陶瓷面板与金属背板的厚度匹配是影响复合靶板抗弹性能的关键因素，对于给定的弹种和材料，存在最佳的厚度匹配。B4C陶瓷/铝合金复合靶板的最佳厚度匹配为H1/H2≈2.6，该计算结果可用于指导穿甲试验设计。

3) 基于Johnson-Cook本构和JH-2本构建立的有限元模型是合理有效的，较好地模拟了陶瓷/金属复合靶板的动态穿甲过程，该方法可拓展到不同形状的动能弹丸正侵彻和斜侵彻陶瓷/金属复合靶板问题的研究。

参考文献：

[1] 侯海量，朱锡，阚于龙．轻型陶瓷复合装甲结构抗弹性能研究进展 [J]．兵工学报，2008，29(2): 208-216.

[2] Wilkins M L. Second Progress Report on Light Armor Program [R]. California: Lawrence Livermore National Laboratory, 1967.

[3] Anderson C E, Burkins M S, Walker J D, et al. Time-resolved Penetration of B4C Tiles by the APM2 Bullet[J]. Computer Modeling in Engineering & Science, 2005, 8(2): 91-104.

[4] Johnson G R, Holmquist T J. Response of Boron Carbide Subjected to Large Strains, High Strain Rates, and High Pressures [J]. Journal of Applied Physics, 1999, 85(12): 8060-8073.

[5] 傅苏黎，丁华东，雷秉强，等．碳化硼基3DMC材料抗弹性能的初步探讨[J]．装甲兵工程学院学报，2003, 17(3): 17-20.

[6] 丁华东，张甲英，许艺，等．碳化硼基双复合装甲板制备与靶试[J]．中国表面工程，2013, 26(3): 86-90.

[7] Johnson G R, Cook W H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures [C]∥Proceedings of the 7th International Symposium on Ballistics. Netherlands: Hague, 1983: 541-546.

[8] 唐志平．冲击相变[M]．北京: 科学出版社, 2008: 14-15.

[9] Holmquist T J, Templeton D W, Bishnoi K D. Constitutive Modeling of Aluminum Nitride for Large Strain, High-strain Rate, and High-pressure Applications [J]. International Journal of Impact Engineering, 2001, 25(3): 211-231.

[10] Johnson G R, Holmquist T J. An Improved Computational Constitutive Model for Brittle Materials [C]∥High Pressure Science & Technology. New York: AIP Press, 1994: 981-984.

[11] Holmquist T J, Johnson G R. Response of Boron Carbide Subjected to High-velocity Impact[J]. International Journal of Impact Engineering, 2008, 35(8): 742-752.

[12] 曾首义，蒋志刚．金属间隙靶板和陶瓷复合靶板研究综述 [J]．防护工程，2009, 31(4): 67-72.