CLAHE优化低频DCT系数重变换的鲁棒人脸识别

王轶冰，胡邦君

WANG Yibing1,HU Bangjun2

1.安徽大学 计算机教学部，合肥 236061

2.安徽省生物研究所，合肥 230088

1.Center of Computer Teaching,Anhui University,Hefei 236061,China

2.Institute for Biological Studies in Anhui Province,Hefei 230088,China

人脸识别是最为常用的生物特征自动识别技术之一[1]，具有方便、非接触式采集和采集成本低等优势，因此在人机交互、自动监控、身份识别等领域具有很大的发展潜力[2]。经过数十年的深入研究，人脸识别已经取得长足的发展，在约束环境下的正面人脸识别率已达到90%以上。但是，当人脸图像采集受外界条件影响（如光照、姿势、表情、遮挡）时，将大大降低识别性能[3]。因此，如何消除光照、姿势、表情等因素对人脸识别的影响，成为亟待解决的问题。

为了解决光照、表情、姿态变化引起的人脸识别率下降的问题，学者们提出了许多不同的人脸识别算法。例如，文献[4]提出使用无监督学习方法对每个人脸图像的微观结构进行编码。针对在剧烈光照变化情况下无法获得足够的特征描述信息的问题，基于梯度幅值自相似性，文献[5]提出了称为梯度边缘幅值模式（Pattern of Edge Gradient，POEM）的判别性特征描述符，取得了很好的识别效果，但是，一定程度上增加了计算开销。有的学者提出利用DCT变换，将特征脸方法与DCT变换或其他变换相结合。例如，文献[6]提出将特征脸与DCT变换和人眼视觉特性加以结合；文献[7]探讨了在不同DCT变换下的特征值与特征向量；文献[8]证明了PCA和LDA可被直接用于DCT变换域上；文献[9]表明，重新变换离散余弦变换（Discrete Cosine Transform，DCT）的低频系数在所有其他光度规范化技术中能得到的性能最佳。文献[10]结合了人脸镜像对称性和核主成分分析，提出了基于对称核主成分分析的人脸识别方法；文献[11]表明，使用核函数可有效地计算高维特征空间的主成分以获取重要的图像信息。

基于上述分析，为了更好地解决鲁棒人脸识别问题，提出了基于限制对比度自适应直方图均衡化（Contrast Limiting Adaptive Histogram Equalization，CLAHE）的DCT系数重变换算法，通过缩减DCT系数补偿光照变化，使用核主成分分析（Kernel Principal Component Analysis，KPCA）提取高维特征向量，最后利用最近邻分类器完成人脸的识别。实验结果表明所提算法在光照变化人脸识别中的有效性及鲁棒性。

1 系统设计

为了提高光照变化人脸识别系统的识别精度，提出的人脸识别算法架构如图1所示，其步骤如下：

（1）对训练图像和测试图像通过使用CLAHE和DCT对图像进行规范化，CLAHE用于局部对比拉伸，DCT变换后，低频系数通过因子降维以消除光照的影响。

（2）得到规范化图像后，使用能够提取高阶统计的KPCA提取图像特征，其中核函数使用多项式核与高斯核。

（3）使用K-最近邻分类器对提取的特征进行分类以完成最终识别。

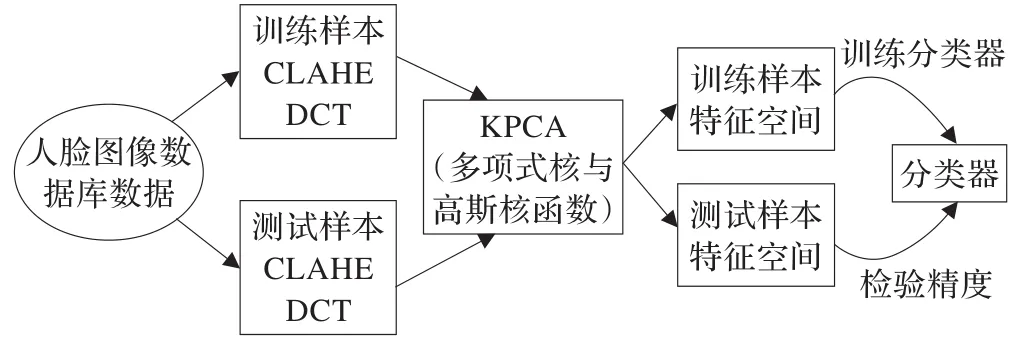
图1 所提算法的大致架构

1.1 限制对比度自适应直方图均衡化

图像的直方图描述了一幅图像的灰度级内容。它是图像处理中一种十分重要的图像分析工具。直方图均衡化以概率理论为基础，运用灰度点运算来实现直方图的变换，能够给出增强的规范化图像，从而达到图像增强的目的。普通的直方图均衡算法对于整幅图像的像素使用相同的直方图变换，这对于那些像素值分布比较均衡的图像来说，算法的效果很好。然而，如果图像中包括明显比图像其他区域暗或者亮的部分，这部分的对比度将得不到有效的增强。

自适应直方图均衡化（AHE）是一种用来提升图像对比度的技术。和普通的直方图均衡化算法不同，AHE通过计算图像的局部直方图，然后重新分布亮度来改变图像对比度。因此，该算法更适合于改进图像的局部对比度以及获得更多的图像细节，即图像内感兴趣的特征需要局部加强。但是，AHE有过度放大图像中相同区域的噪声问题，因此采用限制对比度直方图均衡（CLAHE）[12]算法能有限地限制这种不利的放大。

CLAHE同普通的自适应直方图均衡算法不同的地方主要是其对比度限制。CLAHE首先将图像划分成若干个小区域，其次增强每个小区域的对比度，然后，使用双线性插值合并相邻小区域，以消除人为产生的边界线。另外，通过选择直方图的限幅电平减少未考虑的噪声放大。采用HE和CLAHE后的图像如图2所示。图2中，（a）为原始图像，（b）所示为（a）采用普通直方图均衡化后的图像，（c）所示为采用限制对比度自适应直方图均衡化后的图像。很明显，CLAHE有效地抑制了噪声的增强。

图2 采用HE和CLAHE后的图像对比

1.2 离散余弦变换

离散余弦变换（DCT）是一种优良的数据压缩方法，它具有以下两个特点：

（1）DCT是一种正交变换，各种正交变换都能在一定程度上减少随机向量的相关性，且信号经过大多数正交变换后，能量会集中在少数的变换系数上。去掉对信号贡献较小的系数，仅利用保留下来的信号恢复信号，不会引起明显的失真。而图像具有低频特性，即图像的信息主要集中在低频区域，通过DCT变换，图像的大部分能量都集中在DCT系数图像左上角的一小块区域。

（2）DCT压缩能力仅次于K-L变换，但是K-L变换的基向量依赖于信号向量的协方差矩阵，特征值和特征向量的计算十分困难，而DCT具有快速实现算法（FFT），具有极大的速度优势。以上特点使得DCT得以越来越广泛的应用。

对于一幅 M×N的图像 f(x，y)矩阵，其离散余弦变换定义如下：

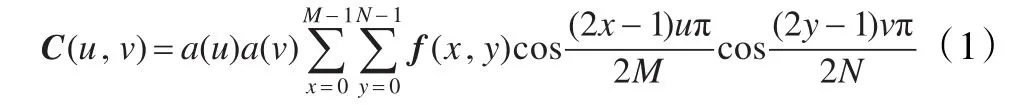
其中，C(u,v)称为矩阵 f(x，y)的DCT系数。u=0,1,…,M-1，v=0，1，…，N-1，a(u)、a(v)分别定义为：

图3 重变换系数不同时的图像对比

经过DCT变换后，图像的二维DCT系数构成一个与原始图像大小相同的矩阵，其低频系数集中在矩阵的左上角，是图像中变化较慢的成分，而高频系数集中在矩阵的右下角，是图像的细节和边缘成分。DCT可以将图像从空域转换到频域，而光照变化主要影响的就是低频部分，这样通过丢弃一定的低频DCT系数就可以有效地实现光照补偿。文献[13]已经在实验上验证了该方法对光照变化具有很好的鲁棒性。图3所示为不同数目的低频DCT系数重新变换的DCT规范化结果。由图3可以看出，重变换DCT系数数目为29时，性能最佳。

1.3 核主成分分析

特征提取是人脸识别系统的主要步骤，因为它能降低脸部图像的维度，最流行的特征提取技术是主成分分析（PCA）。通过主成分分析来进行人脸识别，所提取的特征能较好地反映出人脸的分布信息。但是，PCA在本质上是依据特征向量方差最大的原则提取特征，只利用了图像的二阶特征，未能利用图像数据中的高阶特征，而一幅图像的高阶统计往往包含了图像边缘或曲线的多个像素间的非线性关系，这些信息对图像识别非常有利。为此，学者们将PCA方法推广到高维特征空间，提出了核主成分分析（KPCA）方法。本文算法使用KPCA提取高阶统计，算法过程描述如下：

假设 x1，x2，…，xM为给定的样本集，用{xi}表示输入空间。KPCA的基本思想是通过某种方式将输入空间映射到某个高维空间，并且在该高维空间中实现PCA。假设相应的映射为Φ，其定义如下：

核函数通过映射Φ将隐式地实现点x到F的映射，并且由此映射而得的特征空间中数据满足中心化的条件，即

则特征空间中的协方差矩阵为：

现求C的特征值λ≥0和特征向量：

即有：

考虑到所有的特征向量可表示为Φ(x1)，Φ(x2)，…，Φ(xM)的线性组合，即

则有：

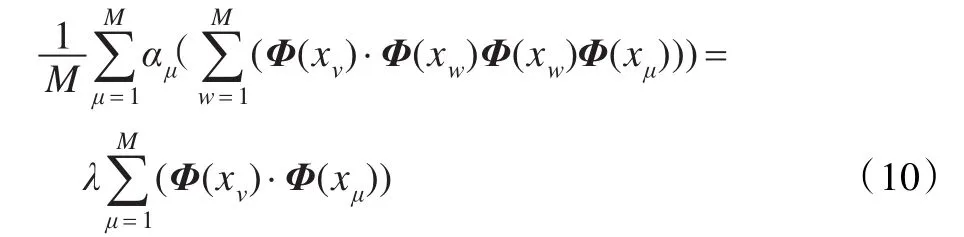
其中，ν=1，2，…，M 。定义 M×N维矩阵K：

因此，式（10）可以简化为：

显然满足：

求解式（13）就可以得到特征值和特征向量。对于测试样本在特征向量空间Vk的投影为：

将内积用核函数替换，则有：

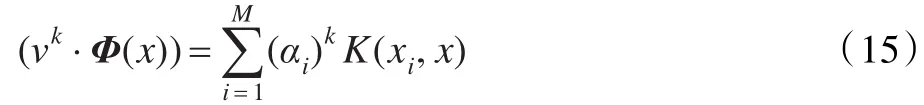
当式（5）不成立时，即特征空间数据不满足均值为0的条件时，则需要进行调整：

因此，核矩阵可以修正为：

常见的核函数有以下几种形式：

（1）线性核函数：

（2）d阶多项式核函数：

（3）高斯核函数：

根据以上分析，使用核函数就能提取非线性主成分，选取式（19）的多项式核函数和式（20）的高斯核函数，因为它们在许多模式分类应用中具有优越的性能。

1.4 最近邻分类

分类在任何一种人脸识别系统中都是非常关键的一步，K-最近邻分类器是最简单、使用最广泛的非参数化分类器，基于特征空间最接近训练实例对对象进行分类。特征提取完成后，分别对训练特征和测试特征进行规一化操作，使其具有零均值和单位方差，然后利用最近邻分类器完成最终的分类、识别。即计算测试样本特征与每个训练样本特征之间的欧氏距离，当测试样本和N种训练样本其中一种的欧氏距离最短时，则测试样本被判断为这种训练样本的类别。

2 实验

2.1 数据集

实验数据主要来自三个人脸数据库，即ORL标准人脸库、扩展的YaleB和AR人脸库。ORL人脸库共有40个人，其中包含了每个人在不同时间、不同光照条件下的10幅不同的人脸图像。每幅图像灰度级为256，尺寸为112×92。实验中，将每幅图像统一裁剪为80×100。扩展的YaleB数据库由38个人，每人64幅在不同光照下的256级灰度图像组成。也将每幅图像预处理为80×100大小。以上两个库均包括了光照、脸部表情和姿势的各种变化。其中人的脸部表情和脸部细节有着不同程度的变化，如笑或不笑，眼睛睁或闭，戴或不戴眼镜等；人脸姿态也有相当程度的变化，深度旋转和平面旋转可达20o；人脸的尺度也有多达10%的变化。AR人脸库是由西班牙巴塞罗那计算机视觉中心建立的，包含了126人（男性70，女性56）的近4000幅图像，该人脸库每个人的表情均不相同，肤色分布较广，部分图片有眼镜、围巾等饰物遮挡。且所有图像采集环境中的摄像机参数、光照环境、摄像机距离等都是严格控制的。

2.2 参数讨论

实验使用MATLAB7.0在个人计算机上实现，计算机配置为：Windows 7操作系统、迅驰酷睿2处理器、2.10 GHz主频、16 GB RAM。

以ORL人脸库为例，首先考察了不同的DCT系数数量对所提算法性能的影响，包括识别的精度和整个算法所耗时间，重变换DCT系数数目分别取7、13、20、29、35、40。图4给出了不同的系数数目对识别精度和识别速度的影响曲线。由图4可以看出，随着DCT系数数量的增加，识别精度呈增长趋势，但是当系数数目增加到一定程度时，系数数目的变化对识别率的影响很小，说明删除的系数对图像重建和人脸识别的影响已经微乎其微了。而增加系数会大大增加系统的识别时间，系统开销就会增加。因此，以下实验中，重变换DCT系数数目取为29。

其次，实验比较了在DCT系数取值相同的情况下，不同的核函数对识别率的影响。核函数分别选择多项式核函数和高斯核函数，表1给出了不同的参数对识别率的影响。由表1可以看出，高斯核函数的识别率明显高于采用多项式核函数的识别率，因此，以下实验中，σ取10。

表1 不同的核函数对识别率的影响（%）

2.3 比较与分析

2.3.1 ORL数据库

在ORL数据库上，首先将该库分为训练库和识别库，其中训练库和识别库分别由200幅人脸图像组成。实验中用到的部分训练图像如图5所示。然后采用几种较为先进的算法，如基于LMP融合KPCA算法[14]、LBP+RB2DLDA算法[15]、对称核主成分分析算法与所提算法进行比较。

图5 ORL数据集中的部分训练样本

当训练样本取不同数目时，各算法的平均识别精度是不同的。实验中，随机抽取每个人的k幅图像作为训练样本，k的取值范围为[2，9]。对每个k进行多次实验然后取平均值，实验结果如表2所示。

表2 各算法在ORL数据集上的平均识别率比较（%）

从表2中可以看出，随着k的增加，各算法的识别率逐渐上升，当k=9时，各算法的识别率都在95%以上，虽然所提算法的识别率高于其他算法，但不能充分体现所提算法的优越性。下面将各算法应用于扩展YaleB库和AR人脸库进行分析比较。

2.3.2 扩展的YaleB数据库

为了和其他算法进行比较，实验选用扩展YaleB库中正面姿态的2432幅图像，并根据不同光照情况，将样本集划分为5个子集：子集A、子集B、子集C、子集D、子集E，用于实验的部分图片如图6所示。

图6 实验选用的部分图像

第一组实验仅选用扩展YaleB子集中理想光照下的人脸图像，即子集A进行训练，而采用其他不同光照条件下的人脸图像，即子集B～子集E进行测试。实验结果如表3所示。由表3中可以看出，所提算法始终能够获得比其他几种方法更高的识别率，尤其是在光照条件差的子集D和子集E中，充分说明其具有较强的鲁棒性。

从表3可以看出，在所有的子集上，所提算法的识别率均高于其他所有比较算法，各算法在子集B、C上的识别率都较为理想，因此不能明显体现出所提算法的优越性，但是在光照条件非常差的子集D、E上，所提算法的识别率仍然保持在较高水平，而其他几种比较算法的识别率却明显下降，由此可以体现出所提的算法在识别率方面的可靠性以及对光照变化的鲁棒性。

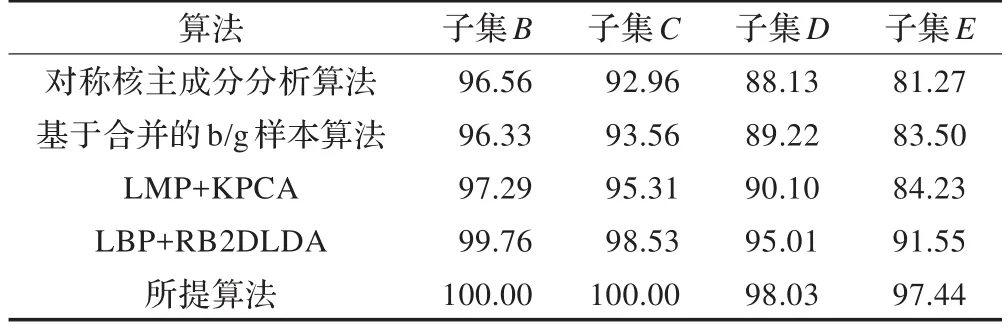
表3 扩展YaleB人脸库用子集A训练时的识别率 （%）

2.3.3 AR人脸库

实验中，从AR人脸库中选择100人（男性50，女性50），每人14张图像。对于每个对象，分别从中选择正常、微笑、生气、左侧光照、右侧光照、眼镜遮挡、围巾遮挡的图像。部分实验样本如图7所示。实验包括两部分：（1）考查训练样本集数目与每类训练样本数均取不同值时，对识别率的影响；（2）将所提算法与其他算法作比较以分析其识别性能。

图7 AR人脸库部分实验样本

首先从100人中随机抽取k个人进行实验，训练样本集数目k的取值范围是[3，10]，每类训练样本数取2、3时，所提算法的识别率如图8所示。

图8 不同k、训练样本数对识别率的影响

由图8可见，随着训练样本集数目的增加，识别率基本呈上升趋势，同时，随着训练样本数的增加，算法的识别率有较大的提高。

为了体现所提算法的优越性，实验中每个人的前7幅图像作为训练样本，后7幅图像作为测试样本，将所提算法的识别率与其他几种较为先进的算法进行了比较，实验结果如表4所示。由表4可以看出，所提算法能获得与这些算法相当甚至是更好的识别率，尤其在有太阳镜、围巾等遮挡物的情况下，所提算法仍能获得明显高于其他算法的识别率，这充分说明本文算法具有良好的鲁棒性。

表4 各算法的识别率比较 （%）

3 结束语

为了改善鲁棒人脸识别系统的识别率，提出了基于CLAHE的低频DCT系数重变换算法。该算法使用CLAHE技术代替AHE对局部进行对比拉伸，即用在每个小区域上操作来代替在整个人脸图像上操作。然后通过缩减适当数目的低频DCT系数来消除光照变化，使用核PCA来提取图像的高阶统计以获得更多图像细节，并利用最近邻分类器进行分类以完成最终的人脸识别。与其他几种较为先进算法的比较表明了所提算法的有效性和优越性。特别是在对AR人脸图像库的实验及对比结果表明，所提算法对人脸遮挡、光照以及表情变化具有较好的鲁棒性。

[1]苏煜，山世光，陈熙霖，等.基于全局和局部特征集成的人脸识别[J].软件学报，2010，21（8）：1849-1862.

[2]Atkins W.Industry squares up to multiple opportunities[J].Biometric Technology Today，2007，15（1）：8-11.

[3]Ma Hui，Hu Fengsong.The study of human face recognition based curvelet transform and 2DPCA[J].ICISE，2010，12（4/6）：5512-5515.

[4]皋军，孙长银，王士同.具有模糊聚类功能的双向二维无监督特征提取方法[J].自动化学报，2012，38（4）：549-562.

[5]杨利平，叶洪伟.人脸识别的相对梯度方向边缘幅值模式[J].中国科技论文在线精品论文，2014，7（4）.

[6]Ramasubramanian D，Venkatesh Y V.Encoding and recognition of faces based on the human visual model and DCT[J].Pattern Recognition，2001，34（12）：2447-2458.

[7]Tseng C C.Eigenvalues and eigenvectors of generalized DFT，generalized DHT，DCT-IV and DST-IV matrices[J].IEEE Trans on SP，2002，SP-50（4）：866-877.

[8]Chen Weilong，Er M J，Wu Shiqian.PCA and LDA in DCT domain[J].Pattern Recognition Letters，2005，26：2474-2482.

[9]Vishwakarma P，Pandey S，Gupta M N.An illumination invariant accurate face recognition with down scaling of DCT coefficients[J].Journal of Computing and Information Technology，2010，18（1）：53-67.

[10]刘嵩，罗敏，张国平.基于对称核主成分分析的人脸识别[J].计算机工程，2012，32（5）：1404-1406.

[11]卢桂馥，林忠，金忠.基于核化图嵌入的最佳鉴别分析与人脸识别[J].软件学报，2011，22（7）：1561-1570.

[12]Celik T，Tjahjadi T.Automatic image equalization and contrast enhancement using Gaussian mixture modeling[J].IEEE Transactions on Image Processing，2012，21（1）：145-156.

[13]Chen Weilong，Meng Joo Er，Wu Shiqian.Illumination compensation and normalization for robust face recognition using discrete cosine transform in logarithm domain[J].IEEE Transactions on Systems，Man，and Cybernetics，PartB：Cybernetics，2006，36（2）：458-466.

[14]郭飞，王成.基于LMP和KPCA的人脸识别[J].计算机工程，2010，36（24）：183-186.

[15]苏立明，王莹.基于局部二元模式和重采样双向2DLDA的人脸识别算法[J].吉林大学学报：理学版，2013，51（3）：459-464.