考虑系统调用和失效模式的软件可靠性模型

薛利兴，左德承，张 展

XUE Lixing,ZUO Decheng,ZHANG Zhan

哈尔滨工业大学 计算机科学与技术学院，哈尔滨 150001

School of Computer Science and Technology,Harbin Institute of Technology,Harbin 150001,China

1 引言

可靠性通常是软件质量要求中的一个关键指标，同时也是保证软件在使用过程中正确运行的度量[1]。随着各种各样的计算机设备已经成为日常生活中重要的组成部分，人们发现软件的失效不再只是软件工程师的事情，还会给我们带来种种不便甚至更严重的后果。因此，可靠性越来越受到人们的重视，尤其是在一些关键应用之中。

当前的软件开发多数是基于组件或模块进行的，但软件整体并不是各个模块的简单相加，每个模块都可能对全局的可靠性产生不同的影响。软件可靠性分析利用软件的整体架构、软件运行剖面、以及每个模块的可靠性搭建数学模型，进而分析软件整体的可靠性。模型一方面可以在设计阶段根据架构、控制流、已知组件可靠性数据或预估的可靠性对软件整体的可靠性进行预测；另一方面也可以应用在软件的验证和运行阶段，通过各种测试方法得到每个模块的可靠性和实际运行环境中的使用剖面，再代入数学模型得到软件的可靠性，从而评估软件是否达到了预期的要求。

在过去的几十年之中，基于模块的软件可靠性研究领域已经取得了不少的成果。然而，在这些研究中，都是将软件独立在运行环境之外，只是纯粹地、抽象地考虑软件自身代码的可靠性，完全忽略了软件所依赖的操作系统及运行环境对可靠性的影响。

事实上，在现代以操作系统负责支撑应用软件运行环境以及用户操作环境的计算机系统中，软件中的每个模块或多或少都要进行系统调用，例如资源分配、文件读写等。而系统调用的执行与用户软件自身代码的执行处在不同的特权级别（privilege level），用户软件代码执行处于最低的特权级别（常称为用户态），操作系统代码执行处于较高的级别（常称为内核态）。特权级别由处理器硬件进行约束和控制，越高的特权级别就拥有越多的访问权限和控制权限，同时也导致发生在较高特权级别的错误有可能带来更严重的后果。以Intel x86架构处理器和Linux操作系统为例，Linux操作系统使用了0号和3号两个级别，分别执行操作系统的内核代码和应用软件[2]，如图1所示。发生在3号特权级别（内核态）的错误最多使应用软件本身崩溃，不会影响操作系统及其他应用软件的运行；而发生在0号特权级别（用户态）的错误可以引发操作系统失效，使整个计算机系统处于不可用状态。

图1 x86处理器特权级别与Linux使用情况

由上可以看出：（1）尽管系统调用所执行的代码并不属于目标软件本身，但其可靠性对整个目标软件可靠性的影响不可忽视；（2）系统调用执行在较高的特权级别之中，可能会给系统带来完全不同的失效模式；（3）当数据错误发生传播、通过调用接口传播到系统调用过程中，可能会引发后果更严重的失效。因此，在分析软件可靠性的过程中不应该忽略软件所依赖的系统调用及其相关的因素。

本文将软件所依赖的系统调用引入软件可靠性分析模型，依据系统调用处于不同特权等级会引发不同失效定义了软件的多种失效模式，同时考虑了软件不同模块之间的错误传播及软件失效模式之间的相互转化，建立了一种考虑软件运行环境的软件可靠性分析模型。具体地，首先在经典模型基础上逐步将系统调用过程、多种失效模式及错误传播加入到模型之中，对模型进行扩展和细化，最终得到更加精确的软件可靠性分析模型。在模型建立后，在一个软件实例中展示了该模型的使用方法，并给出了获得模型中各个参数的具体方法。

2 软件可靠性相关研究

根据Avizienis等人的定义[3]，失效（failure）是指一个系统不能按照所规定的功能正确提供服务；错误（error）是指可能导致系统出现失效情况的状态，一般可以理解为计算、观察或测量值与真实的、规定的或理论上正确的值之间的差异；故障（fault）通常被认为是产生错误的根本原因，包含软硬件设计缺陷、软件代码漏洞、外界环境干扰等多方面因素。系统不能正确提供服务可能以不同的方式表现出来，这些不同的表现方式通常被称为失效模式（failure mode）。

可靠性（reliability）表示系统能够持续提供正确服务的能力，可以定义可靠性为一种概率性的度量指标，即能够正确完成其功能的概率，其数值可以表示为1减去失效的概率。可靠性是软件质量的重要度量，广泛受到程序员、工程师和研究人员的重视，相关的研究成果也是层出不穷。这些研究主要可以分为两大类：软件可靠性增长模型、软件可靠性分析/预测模型。

软件可靠性增长模型是在软件的调试过程中，将软件整体看作一个黑盒模型，通过测试获得软件失效数据，进而预测软件的平均失效时间（Mean Time To Failure，MTTF）[4-6]。黑盒模型只关注软件接口与外界环境的交互，对软件的内部结构毫不关心，因此软件可靠性增长模型无法获得失效数据以外的其他数据，一旦软件发生微小的修改或升级，整个测试过程需要重新进行。

随着软件规模的不断增加和对软件重用性的强调，模块化软件开发逐渐普及，软件中的模块经常被更换或升级，以黑盒测试为基础的软件可靠性增长模型略显力不从心。研究者开始将目光投向了考虑软件内部架构的白盒方法，提出了软件可靠性分析/预测模型。

Cheung最早提出了基于软件架构的可靠性建模方法[7]。他采用马尔可夫过程来抽象软件不同模块之间的控制流，通过对离散时间马尔可夫过程的分析计算得出软件的可靠性，并强调较少的执行可靠性低的模块同样能够提高软件整体的可靠性。Cheung的模型得到了后续研究人员的广泛认可。Wang等研究者扩展了Cheung所提出的模型，对顺序执行、并行执行、后备容错等多种软件执行模式进行了建模[8]。

Sharma等人将可靠性分析与性能分析巧妙地结合起来[9]。Reussner等人将外部服务调用引入了模型之中，并考虑了外部服务与本地连接渠道的可靠性，使其方法可以运用到分布式软件可靠性分析之中[10]。在上述的这些模型和方法当中，都只假设只存在一种失效模式，也没有考虑软件中的错误传播。

Cortellessa和Grassi提出了模块失效未必导致整个软件失效的观点，将错误传播的问题纳入到模型的考虑范围内[11]。Pham在并行执行、后备容错、循环等软件执行模式的基础上加入了错误传播的考查，并采用UML的方法表示软件的架构[12]。

软件的执行离不开底层操作系统等运行环境的支持。在实际情况中，由于软件的系统调用和硬件特权级别的保护使得系统在运行过程中呈现出不同的失效模式。本文同样在Cheung模型基础之上展开研究，根据软件的实际运行环境，将软件进行的系统调用和多种失效模式纳入考虑范围，同时也考虑了软件模块之间的错误传播以及失效模式相互转化的问题，力争建立更加贴近实际情况的软件可靠性分析模型。

3 可靠性分析模型

首先假设软件中没有系统调用且只有一种失效模式，根据Cheung提出的方法基于离散时间马尔可夫过程建立基本的可靠性分析模型；随后，考虑带有系统调用情况，将基本模型扩展成带有系统调用的软件可靠性分析模式；最后，再对软件中的多种失效模式和错误传播行为进行建模，得到更加精确的模型。

3.1 无系统调用的基本模型

根据Cheung的方法[7]，使用状态图来表示软件的行为：一个状态表示一个模块的执行，从一个状态到另一个状态的转移概率由软件运行剖面和模块可靠性计算得到。这样一来，软件的可靠性就可以由状态的执行顺序和各个独立状态的可靠性来决定。假设软件下一个被执行的状态（模块）只与当前正在执行的状态（模块）有关，与之前的执行顺序没有任何关系，整个状态图和状态转移过程就构成了一个离散时间马尔可夫过程。

假设软件中有n个模块，分别记为 M1，M2，…，Mn，每一个模块对应状态图中的一个节点（即状态图中的一个状态）。对于其中任意的两个节点Mi和Mj，有向边(Mi，Mj)表示软件控制流存在从模块Mi转移到模块Mj的可能性，且用概率Pij表示发生这种控制流转移的可能性。也就是说，当模块Mi执行完毕后，接下来执行模块Mj的概率是Pij。若状态图中不存在有向边(Mi，Mj)，表示模块Mi执行完毕后下一个执行的模块不会是Mj，此时Pij=0。Pij可以通过实验统计来获得，用t(i，j)表示多次实验中从模块Mi到模块Mj控制流转移的平均次数，Pij可以表示为：

需要注意的是，在状态图中Pij并不是从状态Mi转移到状态Mj的转移概率。在软件运行过程中，只有模块Mi正确执行，控制流才有可能跳转到下一个模块Mj。设Ri为状态 Mi的可靠性，用 p(i，j)表示从状态 Mi转移到状态Mj的转移概率，则

不失一般性，假设软件有唯一的入口和出口，分别为 M1和 Mn。集合{M1，M2，…，Mn}是离散时间马尔可夫过程的状态集合，其中M1是初始状态、Mn为终止状态，P=[p(i，j)]为状态转换矩阵。

pk(i，j)表示经过k次转移从状态 Mi到达状态 Mj的概率，则经过k次转移从状态Mi到达状态Mj的可靠性可以表示为：

软件的可靠性是从初始状态M1到达终止状态Mn的概率，发生转移的次数可能是0到正无穷（其中0是一种M1=Mn的特例）。因此，软件的可靠性R可以表示为：

设矩阵U=[u(x，y)]为：

其中I为单位矩阵，由线性代数相关知识可以得到：

同时，显然可知：

将其代入公式（5），可得：

综上，只要得到状态转移矩阵后，可以根据公式（7）和公式（9）得到软件的可靠性。

3.2 考虑系统调用的可靠性模型

在现实中，多数的软件模块中或多或少进行了系统调用。尽管在宏观上看软件中只是一个模块的执行，但从微观看执行过程存在着模块自身代码与系统调用交替执行的不同阶段，如图2所示。对于含有系统调用的模块，其可靠性不仅与自身代码有关，还与其依赖的系统调用密不可分。

图2 带有系统调用的模块执行过程

直观上，带有系统调用模块的可靠性貌似应该由自身代码的可靠性与系统调用的可靠性相乘得到。然而，由于使用者的不同或任务不同，模块中系统调用的次数可能存在一定的随机性，将二者的可靠性简单相乘并不能反映真实情况；同时将系统调用的失效隐藏在模块内部，很难发现模块脆弱的真正原因。此外，系统调用的代码并不属于模块本身，代码风格迥异，亦可能并不开源，测试方法也完全不同，应予以分别进行考虑。因此，将系统调用从模块内部中提取出来，作为调用返回模式[8，13]（call-and-return style）来进行处理。也就是说，将每个系统调用都看成软件中的一个独立的特殊模块，即执行完毕后控制流确定（返回调用模块）的模块。

设模块Mi内部调用了Ai个不同系统调用，其中Ai为非负的整数，i=1，2，…，n，则整个系统的状态图中增加了个状态，即共有个模块。需要注意的是，增加的这些系统调用中有可能是调用的同一个系统调用，但由于其执行完毕的返回控制流不同（返回不同的模块），在这里将它们看成不同的模块。

对于新的状态图中两个任意的节点Mi和Mj，控制流转移概率P～ij的获得方法依然可以按照公式（1）来计算。每个模块的可靠性用R～i表示，从状态Mi转移到状态Mj的转移概率 p～(i，j)构造方法如下：

第一种情况是模块Mi内部调用系统调用Mj，由于系统调用发生在模块Mi执行过程中，无论Mi是否可靠都要按概率进行系统调用，因此不需要考虑Mi的可靠性；第二种情况是系统调用Mj执行完毕返回调用模块Mi，由于调用结束后控制流已经是确定的，只要系统调用正确执行，必然返回Mi，转移概率等于Mj的可靠性；第三种情况模块Mi和Mj都不是系统调用模块，必须在Mi正确执行且控制流有转向Mj可能性的前提下才能发生状态转移。

这样，就得到了新的离散时间马尔可夫过程，其状态空间为{M1，…，Mn…，Mn+A1+…+An}，转移矩阵为 P～=[p～(i，j)]。该带有系统调用的可靠性模型同样只考虑了一种失效模式且不考虑错误传播，软件可靠性计算方法与3.1节中无系统调用的基本模型相同，这里不再赘述。

3.3 失效模式和错误传播建模

在上述考虑系统调用的可靠性模型基础上，尝试对软件中的多种失效模式和错误传播进行建模。为方便起见，重新假设软件抽取系统调用模块后在状态图中共形成n个模块，集合SELF表示所有抽取系统调用后的自身代码模块，用集合CALL表示所有系统调用模块，SELF∪CALL={M1，M2，…，Mn}。同时假设软件出口模块和入口模块均唯一，分别为 M1和 Mn，M1，Mn∈SELF。各模块之间的控制流转移概率Qij依然可以通过公式（1）计算得到。

由于常见的操作系统只使用了两个特权级别，分别对应操作系统的内核态和用户态，可引发两种不同的失效：用户态失效和内核态失效，分别编号为1和2。同时，为了叙述方便和表示方法的统一，将未发生失效作为一种特殊的失效模式，标号为0。设在任一个模块Mi内部，这三种失效模式都可能发生相互转换，且定义函数 fi(x，y)为模块Mi内各失效模式的转换概率：

其中 0≤x，y≤2，并且函数fi(x，y)满足

当x和 y数值变化时，fi(x，y)可以表示模块 Mi的一些属性和错误传播行为：fi(0，0)表示模块Mi可靠性；fi(0，1)与 fi(0，2)分别表示 Mi发生用户态失效和内核态失效的概率；fi(1，1)与 fi(2，2)分别表示用户态失效和内核态失效透过模块Mi的概率。

在考虑了失效模式之后，便无法使用一个节点表示一个模块中的所有状态，此时需要对每个节点进行扩展。对于任意的模块Mi，其输入有三种失效模式；由于考虑了错误传播，失效模式可以在模块内部发生相互转化，模块Mi的输出也可能存在三种失效模式。因此，将模块Mi在状态图中的1个节点扩展成6=（3+3）个节点：3个节点分别表示模块Mi在输入为三种不同失效模式下的执行过程，记为 MIi={MIi1，MIi2，MIi3}，分别表示模块Mi输入为未失效、用户态失效、内核态失效的执行过程；另外3个节点表示模块Mi执行完毕所处的失效模式，记为 MOi={MOi1，MOi2，MOi3}，分别表示模块 Mi执行完毕的状态为未失效、用户态失效、内核态失效。扩展后的节点如图3所示。

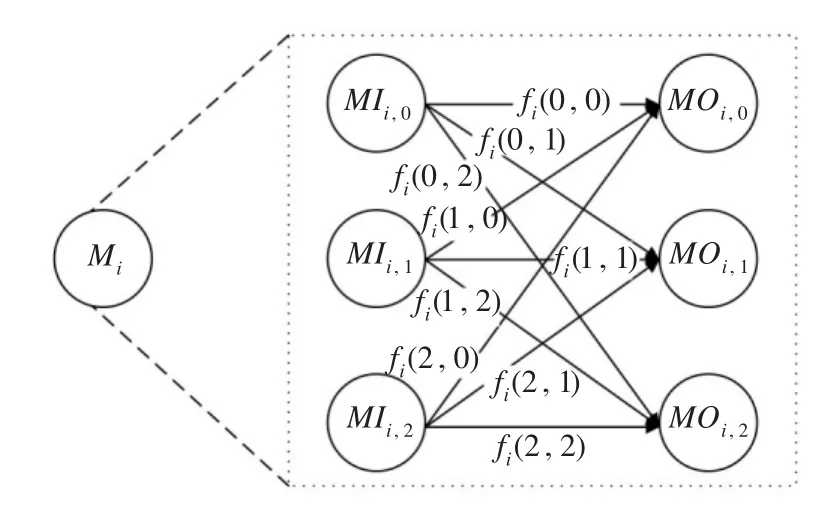
图3 模块节点的扩展

特别地，对于模块Mi在执行过程中进行系统调用模块 Mj的情况，在 Mi的执行状态 MIiα中按概率转移到状态MIjα执行系统调用；MIjα执行完毕后发生状态转移到MOjβ（若执行过程中失效模式没有改变则α=β，否则α≠β）；在进入状态MOjβ后，就表示系统调用执行完毕，将必然返回调用模块Mi，转移到状态MIiβ。图4是一个带有系统调用节点扩展的例子，图4（a）是局部的控制流，模块 M1进行了系统调用，调用模块M3，图4（b）是扩展后的状态图。

图4 带有系统调用节点的扩展实例

用这些状态构造一个离散时间马尔可夫过程用来分析软件的可靠性，状态空间为：

状态转移矩阵为Q=[q(s，t)]，具体构造如下：

第一种情况是模块Mi进行调用系统调用模块Mj，调用概率与Mi的失效模式无关，等于控制流转移的概率；第二种情况是执行系统调用Mi过程中发生的失效模式转换；第三种情况是系统调用模块Mi执行完毕后返回模块Mj，执行完毕后必然返回；第四种情况是在模块Mi执行过程中发生的失效模式转换；第五种情况是模块Mi执行完毕继而执行模块Mj，此时不会再发生系统调用，转入模块Mj的概率是转入该模块的控制流转移概率与所有可能转入模块的控制流概率之和的比值；对于其他情况，状态转移的概率为0。

在该模型中，软件的可靠性是从初始状态M1，0到达终止状态MOn，0的概率，其推导方法与3.1节中相同，这里不再赘述。

4 应用实例

选取了Linux操作系统下一个自己编写的简单系统来演示如何应用上述的可靠性分析模型，软件结构如图5所示。

图5 软件基本结构

在这个实例中，软件有两种失效：自身崩溃和操作系统失效，分别编号为1、2，且均为停止运行失效；软件正确执行编号为失效模式0。

表1 模块M1实验数据

表2 模块M2实验数据

表3 模块M3实验数据

表4 模块M4实验数据

表5 模块M5实验数据

表6 模块M6实验数据

表7 模块M7实验数据

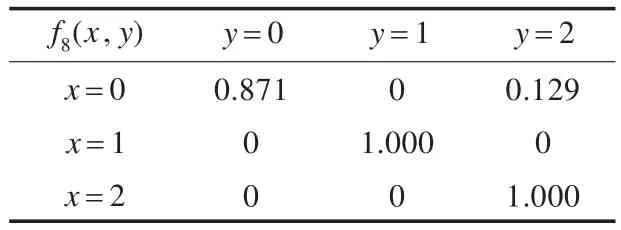
表8 模块M8实验数据

表9 模块M9实验数据

4.1 系统调用与控制流数据

系统调用和控制流的获取采用实验统计的方法获得。在运行软件的同时，使用OProfile等系统分析工具跟踪记录软件中各模块的控制流转移情况和发生次数、各模块内部系统调用情况和调用次数。在软件长时间运行之后，根据得到的数据计算后可得控制流的转移概率。

具体地，得到的程序控制流如图6所示，其中，自身代码集合 SELF={M1， M2， M3， M4} ，系统调用集合CALL={M5，M6，…，M11}，这 11 个模块的控制流转移概率为：

图6 软件的控制流

4.2 失效数据

对于系统调用模块Mi(i=5，6，…，11)，只可能发生失效模式2，即运行过程中只会出现失效模式0和失效模式2，且失效模式2不会向其他失效模式转换。借助CMU的Ballista测试[14]来获得每个系统调用的失效率 fi(0，2)，而每个系统调用模块的可靠性 fi(0，0)=1-fi(0，2)。

另一方面，对于自身代码模块 Mi(i=1，2，…，4)运行在用户态不可能出现失效模式2，且失效模式1也不会向其他失效模式再次转换。采用算法BR进行大量的随机测试获得 fi(0，1)，而 fi(0，0)=1-fi(0，1)。

算法（BR）

（1）对于每个模块 Mi∈SELF，执行步骤2～7；

（2）生成 Mi的测试用例集合TESTi；

（3）计数器TotalCount和 FailCount初始化为0；

（4）对于每个测试用例α∈TESTi，执行步骤5～6；

（5）以α为输入运行 Mi，同时递增TotalCount；

（6）若模块Mi失效，根据输出信息判断失效原因，若不是系统调用引起，递增FailCount；

（7）根据计数器的数值计算模块Mi的失效率

通过实验得到的数据如表1～11所示。

表10 模块M10实验数据

4.3 可靠性结果

根据已经获得的各项参数，可以建立一个66×66的稀疏状态转移矩阵。应用Matlab进行矩阵的计算，最终该软件在Linux环境下运行的可靠性为0.472。

表11 模块M11实验数据

5 结束语

本文在经典的软件可靠性分析/预测模型基础上考虑了运行环境对可靠性的影响，将软件中的系统调用从软件自身模块中抽取出来作为特殊的模块并考虑了多种失效模式，提出了一种更贴近实际的软件可靠性分析模型。尽管在应用过程中，该模型的状态空间比传统模型有所增加，但状态转移矩阵为稀疏矩阵，只需要计算特定的非零元素即可，同时可以应用Matlab等数学软件进行矩阵的辅助计算。

此外，由于不同的操作系统中内核代码可靠性各不相同，软件运行的可靠性也随之受到影响，该模型可以有效体现出不同操作系统对软件可靠性的影响。同时，该模型适用于常见的系统架构和Windows、Linux、MacOS、Unix等常见的操作系统，在为特定软件选择运行环境时也可具有一定的应用价值。

[1]Laprie J C.Dependability of computer systems：concepts，limits，improvements[C]//SixthInternational Symposium on Software Reliability Engineering，Oct 24，1995—Oct 27，1995.California：IEEE，1995：2-11.

[2]Intel.Intel 64 and IA-32 architectures software developer’s manual[M].California：Intel，2013.

[3]Avizienis A，Laprie J C，Randell B，et al.Basic concepts and taxonomy of dependable and secure computing[J].IEEE Transactions on Dependable and Secure Computing，2004，1（1）：11-33.

[4]Lyu M R.Handbook of software reliability engineering[M].New York：McGraw-Hill，1996：71-117.

[5]Goel A L.Software reliability models：assumptions，limitations，and applicability[J].IEEE Transactions on Software Engineering，1985，SE-11（12）：1411-1423.

[6]Ramamoorthy C V，Bastani F B.Software reliability：status and perspectives[J].IEEE Transactions on Software Engineering，1982，SE-8（4）：354-371.

[7]Cheung R C.A user-oriented software reliability model[J].IEEE Transactions on Software Engineering，1980，SE-6（2）：118-125.

[8]Wang W，Pan D，Chen M.Architecture-based software reliability modeling[J].Journal of Systems and Software，2006，79（1）：132-146.

[9]Sharma V S，Trivedi K S.Quantifying software performance，reliability and security：an architecture-based approach[J].Journal of Systems and Software，2007，80（4）：493-509.

[10]Reussner R H，Schmidt H W，Poernomo I H.Reliability prediction for component-based software architectures[J].Journal of Systems and Software，2003，66（3）：241-252.

[11]Cortellessa V，Grassi V.A modeling approach to analyze the impact of error propagation on reliability of component-based systems[C]//10th International ACM SIGSOFT Symposium on Component-Based Software Engineering，Jul 9，2007—Jul 11，2007.Germany：Springer，2007，4608：140-156.

[12]Thanh-Trung P，Defago X.Reliability prediction for component-based systems：incorporating errorpropagation analysis and different execution models[C]//12th International Conference on Quality Software，Aug 27，2012—Aug 29，2012.Washington DC：IEEE，2012:106-115.

[13]Wang Wenli，Wu Y，Chen Mei-Hwa.An architecture-based software reliability modeling[C]//1999 Pacific Rim International Symposium on Dependable Computing，Dec 16，1999—Dec 17，1999.Washington DC：IEEE，1999：143-150.

[14]Koopman P，Devale J.The exception handling effectiveness of POSIX operating systems[J].IEEE Transactions on Software Engineering，2000，26（9）：837-848.

[15]Nomizu K.Fundamentals of linear algebra[M].New York：McGraw-Hill，1966.