基于粒子滤波算法的神经丝自动跟踪

袁亮

Yuan Liang

新疆大学机械工程学院，新疆乌鲁木齐市 830047

School of Mechanical Engineering, Xinjiang University, Urumqi, Xinjiang, 830047

1 介绍

生物细胞的功能主要取决于细胞内物质积极和定向运动1。这些物质非常多样，包括细胞内蛋白质复合物，细胞骨架聚合物，核糖核蛋白颗粒，和膜细胞。由于荧光显微镜功能强大，可以对活细胞内移动结构直接观察2，这就使得它成为我们研究这些物质的运动的强有力工具。为了提取所产生的图像序列的动力学数据，我们采用实时或延时视频录像以在线或离线的方式跟踪大量随时间变化的运动目标。

神经细胞内运动的重要例子是轴突上的运动，这是沿神经细胞轴突上的亚细胞和分子结构运动3,4。轴突的一个有趣的特点是：他们是非常细长的圆柱形突起，通常直径上只有几个微米，但长度可达几个毫米、厘米、甚至米。因此，轴突通常是将一个复杂的三维运动模型减少到一维模型，其中大部分沿轴突的长轴向前或向后移动，如图1所示。

图1 神经丝蛋白质在培养的老鼠皮质神经元轴突中运动的例子。

神经丝蛋白质在轴突上运动，测量直径约10纳米，长几微米5，是轴突细胞骨架的主要组成部分。它对齐于平行轴突的长轴做间歇的双向移动，这种移动是停顿时间长短不同的短时间向前或向后运动6,7。该微丝移动迅速平均速率约0.5微米/秒，但其整体运动速度却要慢得多，因为他们要花大量的时间暂停7。由于运动的持续时间，以及移动和暂停状态之间频率的转变都是高度可变的，因此其运动可视为随机过程。为了分析运动动力性能，我们必须在连续帧视频中跟踪神经丝蛋白质。然而，目前这一过程完全由手动完成，这大大增加了劳动强度和人为错误影响8。因此，建立一个完全自动跟踪方法是必要的，这样可以提高跟踪效率和消除人工操作引起的主观性和潜在的可变性。

2 国内外研究概述

视频跟踪已应用于各种不同类型的细胞内运动，例如9,10,11。传统的细胞内跟踪方法分为两个主要步骤：检测和定位，对应。在检测和定位的步骤中，目标的位置是通过局部图像降噪和分割来确定的。关键是对应步骤，就是要在连续帧的视频之间建立同一物体的对应关系。由于若干因素的影响，包括快速运动，物体变形，图像噪声，对象合并和分裂等等，这使得跟踪细胞内运动的目标变得较为困难。Jaqaman等人12,13提出了一种跟踪算法，被称为线性分配法，这种方法可以在对应步骤中解决对象消失，合并和分裂的问题。Yang等人14基于Kalman滤波方法设计了可靠的跟踪大规模密集反平行粒子运动的方法。然而，他们的方法对低信噪比图像无法工作15,16。对于跟踪有噪声图像序列中的物体，Smal17等人提出了一种使用粒子滤波的鲁棒算法。他们的方法考虑到衍射极限对象的光学模糊，用一个点扩展函数模型计算观测模型的可能性。然而，这种方法使用通用粒子滤波，增加了计算负担。这是因为在通用粒子滤波算法中，为保证数据的可靠性，必须使用大量粒子，而每个观察的粒子都需要一个二维的模型计算。当粒子的数量增加时，总的计算时间就会快速增加。

在本文中，我们提出了一种新的空间约束的粒子滤波跟踪方法。这种方法最鲜明的特点是在神经丝蛋白质的跟踪运动中利用轴突的几何形状。简单地说，我们利用了轴突狭长的突起结构并且轴突上运动的物体必须在轴突内运动。因此，在空间上对先验动态状态能进行约束，从而明显降低了在下一个视频中可能性状态分布的方差。这样，在不影响跟踪精度的情况下可以减少一些粒子的使用量，从而提高了跟踪效率和准确性。

3 轴突约束的粒子滤波算法的实现

3.1 轴突路径建模

正如图1所示，培养的神经元轴突跟踪轨迹为一条光滑曲线。为了建立这个模型的形状，我们使用三次样条插值获得近似的分段多项式轴突路径。利率曲线被节点分为多条线段，每条线段是由不同的多项式样条插值函数建模而成。[u; v]是任何像素在图像坐标系统的位置。对于给定节点的水平坐标u，每一段曲线段的垂直坐标v由三次样条插值函数给定：

这里i代表节点下标(1,2, …, n),c0i，c1i，c2i和 c3i是每个部分的多项式系数并可以使用实际的像素坐标内曲线计算。这样，假如曲线被分为n - 1段，4n个参数能被确定。为了获得这4n个未知参数，要求有4n个条件：位置，连续性，一阶导数的连续性，二阶导数在节点两边界条件。一个自然样条，即在其中的两端不封闭，边界条件是让二阶导数在两个端点处等于零。图2显示仿照这种方式的轴突实例。由于神经丝蛋白质的运动受到轴突的限制，我们使用这个路径定义轴突的中轴线。为了得到神经丝蛋白质路径，我们在整个视频序列中将最大像素强度投影到同一平面上(图2b)，然后我们手动地分出节点(图2c)。

图2 用三次样条差值建立轴突模型。 (a)运动神经丝蛋白质,(b)是整个视频序列每一图像的最大强度投影,(c)是通过重叠在最大强度投影图像上的三次样条插值（白线）获得的曲线拟合结果。

3.2 神经丝蛋白质状态的建模

在跟踪应用中，动态状态的元素选择依据是对象的运动特性。要跟踪一个非对称的移动物质，如神经丝蛋白质，所需的元素包括位置，速度和方向。为方便起见，我们将神经丝蛋白质的外观模型设定为一个边界框长度（l）和宽度（w）的矩形的方块。那么此框就表示滤波算法中的粒子。然后，我们根据移动神经丝的长度和轴突的弯曲程度分别为每个视频序列选择边界框的尺寸。对于直的轴突一个窄框是足够的，但是对于有急弯的轴突，我们必须增加边界框的宽度，来保证能在所有帧中采样到完整的神经丝蛋白质。在时间t的边界框的位置、速度和方向可以由动态定义，这里表示在图像中坐标系方块中心的位置，θt表示方块的转角是对应的速度。动态状态可表示为如下形式：

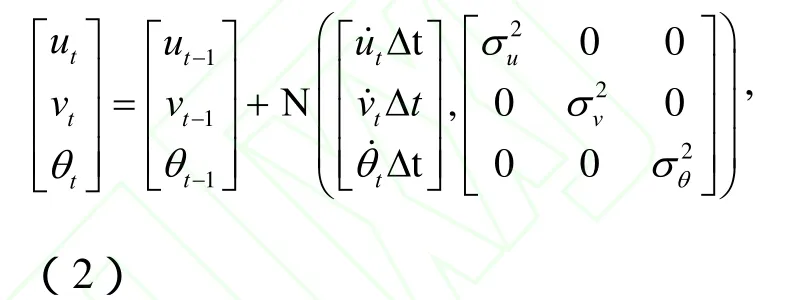
这里Δt是两祯之间的时间间隔。Ν表示正态分布，σu,σv和σθ分别是分布和θt的方差。我们这里使用正态分布是由于重要性密度函数具有高斯形式。在方程(2)中的均值和方差可以根据经验来选择。应该指出的是，我们除了位置和速度之外还使用转角来确定的动态状态，这与许多跟踪方法不同。方向变量也许用于跟踪轴突运输中的球状物质时不那么重要，但是当用于跟踪细胞骨架聚合物如神经丝蛋白质时却非常重要，因为这些物质是长的不对称结构。

使用三个决定动态状态的向量元素序列(u, v,和θ)的结果是产生大量的粒子，这将会降低粒子滤波算法的工作效率。但是，粒子的数量可以通过约束多个向量元素来降低。

3.3 方向约束建模

由于神经蛋白质必须在轴突路径上运动，所以粒子的方向在某个特定位置上必须与轴突的位置保持一致。这也就是，在时刻t的方向θt应当是轴突方程v(ut)的切角方向。相应地，动态状态模型方程(2)可以改写为：

并且

我们称含有方向约束的粒子滤波算法为方向约束粒子滤波(orientationally constrained particle filtering(OCPF)).

3.4 位置约束建模

除了对神经丝蛋白质方向进行约束外，轴突也限制了蛋白质位置。为了对位置约束建模，我们仅限粒子滤波算法中的粒子分布在三次样条曲线拟合程序所定义的轴突上。考虑到三次样条曲线插值的不准确，我们用一个宽度为2d∗的很窄的条来代表轴突，这里窄带的中心线就是轴突的三次样条曲线(图3所示)。d∗是由曲线的拟合误差决定的。假如在时刻t一个粒子到中心线的距离(dt)小于d∗,这个粒子就被接受；如果dt>d∗,神经经蛋白质在这个位置的可能性就为零，这个粒子就是被拒绝。这种运动神经丝蛋白质的位置约束就可以建模为：

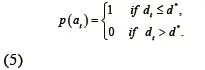
现在整个先验动态状态方程就能改写为：

联合位置约束方程(6) 和方向约束方程(3)和(4)，我们用接受－拒绝机制来产生粒子，具体如下三个步骤：

Step 1: 根据(3)和(4)产生粒子tx′;

Step 2: 计算距离(td);

Step 3: 假如 dt＜d*,接受这个粒子xt′为xt;否则，返回Step 1.

现在粒子可以从位置约束动态模型和方向约束动态模型中产生。我们称这个方法为空间约束粒子滤波（spatially constrained particle filtering (SCPF)）.

图3 t时刻粒子在轴突边界内的分布概略图。实线代表三次样条插值描述的轴突中心线，虚线代表轴突边界。黑色矩形框代表在定义的轴突约束下的轴突内粒子的分布。粗黑色矩形框表示在这个最大似然估计例子下的粒子，它对应于神经丝蛋白质的位置。

4 实 验

实验设置如下：所有的实验序列都是从小鼠大脑皮质分离的神经元中记录下来的，该项工作由美国俄亥俄州立大学Anthony Brown教授实验室中完成。从显微镜测得的原始图像为512×512像素，倍率为0.131µm/像素。首先，我们将进行跟踪初始化和参数描述，然后我们将介绍的跟踪实验的结果。

4.1 跟踪算法初始化和参数

所有神经丝蛋白质都大约10纳米宽。经验上，我们认为用10个像素的（大约650纳米）矩形框宽度w足够在我们的图像中包围一个神经丝蛋白质。移动神经丝的长度是易变的，但平均是5－10微米长。这样，我们设定矩形框的宽度为10个像素，长度随跟踪神经丝长度的不同而相应变化。从中心到两边的距离d∗都选为5个像素。在水平和垂直方向的粒子分布的高斯噪声方差(uσ和vσ)大致设定为25像素，粒子方向的方差(θσ)设定为0.5 rad。在观测似然性的计算中，参数λ设定为20。这种跟踪算法使用Python在2.1GHz的英特尔酷睿2双核计算机上运行。为了计算神经丝蛋白质的实际运行速度，我们使用了MetaMorph软件手动跟踪神经丝蛋白质的运动。这个速度用作参考值来计算自动粒子跟踪算法中的误差。

4.2 实验结果

我们的实验包括通用粒子滤波跟踪，方向约束粒子滤波跟踪，空间约束粒子滤波跟踪，并对其性能进行了评估和比较。图4 (a) 和(b) 显示出采用通用粒子滤波算法中的100和200个粒子的跟踪结果。从图中可以看出无论在位置还是在方向上都出现了大量的跟踪误差，即便200个粒子的跟踪结果会比100个粒子略为好一些。这样，100个和200个粒子的通用粒子滤波算法无法用于跟踪这些录像中的神经丝蛋白质。图4 (c) 和(d) 显示了采用50个和100个粒子的方向约束粒子滤波算法的跟踪结果。正如我们在图4 (c)中所看到的，50个粒子的方向约束粒子滤波算法在某些祯中仍然存在着跟踪误差。图4(d) 显示出了100个粒子的跟踪精度有所提高，但仍然不能满足所有祯。图4 (e) 显示了仅仅50个粒子的空间约束粒子滤波算法表现出了最佳的跟踪结果。

图4 三种不同粒子滤波算法跟踪结果的比较。这些数据对应于视频中的第42，50，52，55，61，和77帧。(a) 100个粒子的通用粒子滤波算法(GPF) 。(b) 200个粒子的通用粒子滤波算法(GPF) 。(c) 50个粒子的方向约束的粒子滤波算法(OCPF)。(d) 100个粒子的方向约束粒子滤波算法(OCPF) 。(e) 50个粒子的空间粒子滤波算法(SCPF) 。在(a)，(b)，(c)，(d)和(e)上排表示粒子在跟踪时的分布，下排表示跟踪结果。

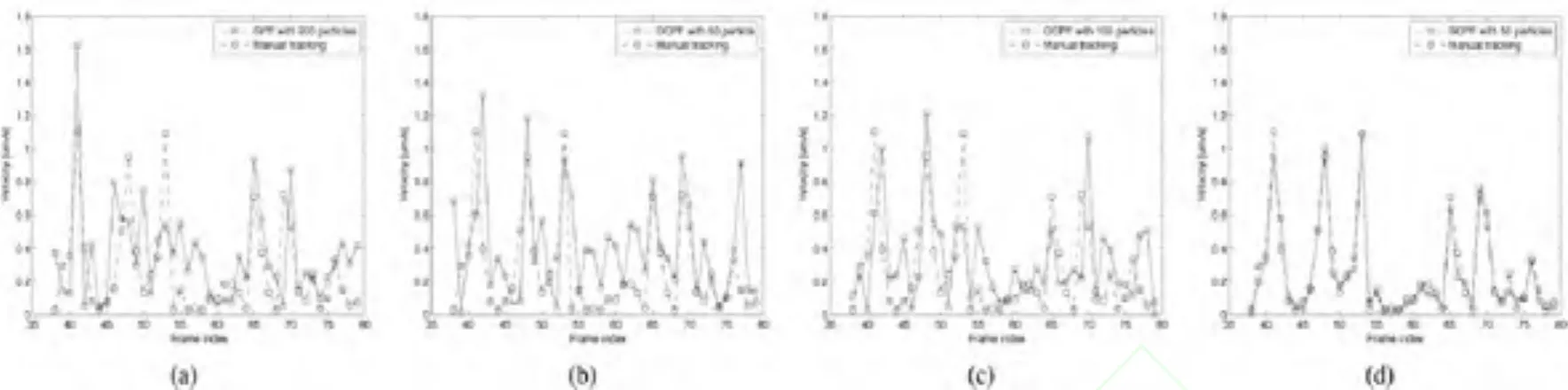
图5 三种不同粒子滤波算法估计的神经丝蛋白质运动速度和实际的运动速度的比较。 (a)200个粒子的通用粒子滤波算法(GPF)。(b)50个粒子的方向约束的粒子滤波算法(OCPF)。(c)100个粒子的方向约束粒子滤波算法(OCPF)。(d)50个粒子的空间粒子滤波算法(SCPF)。注意：使用 GPF和OCPF获得的估计速度和实际速度有相当大的差异，而使用SCPF获得的估计速度与实际速度很相近。

图6 三种不同粒子滤波跟踪算法跟踪误差的比较。(a)200个粒子的通用粒子滤波算法(GPF)。(b) 50个粒子的方向约束的粒子滤波算法(OCPF)。(c)100个粒子的方向约束粒子滤波算法(OCPF)。(d)50个粒子的空间粒子滤波算法(SCPF)。

为了进一步分析空间约束粒子滤波算法的跟踪效果，每个跟踪实验我们使用通用粒子滤波算法、方向约束粒子滤波算法和空间粒子滤波算法分别重复执行了100次，并计算每个时间间隔神经丝蛋白质速度跟踪误差的平均值和标准偏差。跟踪误差定义为实际速度（通过有经验专家手工跟踪获得）和估计速度（用粒子滤波算法法是计算有效粒子的数量(Neff)，具体公式如下：自动跟踪获得）的比值。图5显示了用200个粒子的通用粒子滤波算法，50个和100个粒子的方向约束粒子滤波算法以及50个粒子的空间约束粒子滤波算法的跟踪速度和手动跟踪的速度相比较。图6显示出了相应的均值跟踪误差。200个粒子的通用粒子滤波在每一帧中都显示出了大量的跟踪误差；50个和100个粒子的方向约束粒子滤波算法也不能得到令人满意的跟踪结果。空间约束粒子滤波算法产生的跟踪误差最小，产生的速度也最接近于手动跟踪结果(如图5(d)和图6(d))。这些结果表明通用粒子滤波算法无法用于跟踪延时视频图像序列中的运动神经丝蛋白质。跟踪效果能通过方向约束来提高，最好是同时使用方向和位置这两个约束。

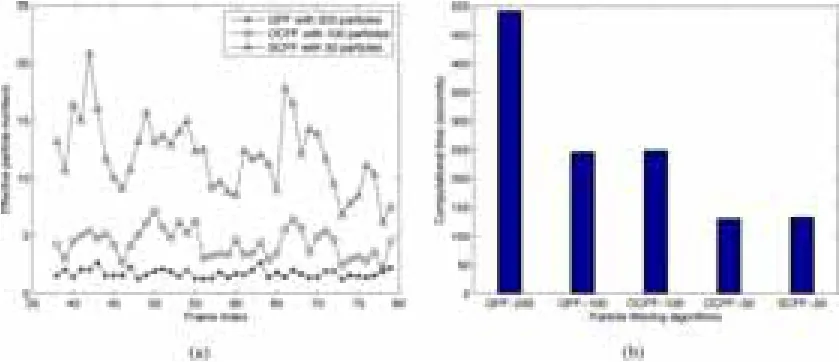
图7 不同跟踪算法的有效粒子数量和计算时间的比较。(a) 有效粒子数量。星号，空心圆和空心三角分别代表使用200个粒子的GPF，100个粒子的OCPF，和50个粒子的 SCPF所获得的数据。(b) 计算时间。

为了进一步检验通用粒子滤波算法，方向约束粒子滤波算法和空间约束粒子滤波算法的运行效率，我们比较了他们的运行时间。在所有粒子滤波算法中，计算时间原则上由粒子的数量和根据观测模型的粒子估计来决定。本论文中，我们在不同算法中使用了同一观测模型，因此计算时间基本上与粒子使用的数量成正比。这样50个粒子的空间约束粒子滤波算法的计算时间是100个粒子的方向约束粒子滤波算法计算时间的一半，是200个粒子的通用粒子滤波算法计算时间的四分之一(图7(b))。因此，与通用粒子滤波算法和方向约束粒子滤波算法相比，空间约束粒子滤波算法对在轴突上跟踪神经丝蛋白质运动更准确和效率更高。

5 结论

轴突神经丝蛋白质运动行为的非线性和不稳定性对自动跟踪算法提出了挑战。由于粒子滤波在处理非线性和不确定性运动的优越性能，它很自然的被用来解决这个问题。然而，由于通用粒子滤波必须使用大量的粒子来实现有效的跟踪,这使得它的计算强度较高。在本文中，我们提出了一个新的空间约束的粒子滤波方法跟踪神经丝蛋白质。这种方法利用神经丝蛋白质的运动范围被限制在一个狭长的轴突内这一特点，对神经丝蛋白质可能的运动方向和位置进行了动力学限制。为了将这两种约束用到粒子滤波算法中，我们利用三次样条插值建立轴突路径的模型，使粒子的位置限制在一个狭窄的路径上，位置的方向限制在轴突路径曲率的切线方向。同时使用这两个约束增加了有效粒子数，从而减少了动态模型的不确定性。为了进行测试，我们比较了空间约束的粒子滤波与通用粒子滤波，以及其中只考虑方向约束的粒子滤波。结果表明，空间约束的粒子滤波方法在效率上大大高于通用或定向约束的粒子滤波方法。因此有必要采取位置和方向的两个限制实现最优跟踪效率。

1 D. Bray. Cell Movements: From Molecules to Motility [M]. 2nd ed. New York: Garland Science, 2000.

2 R. D. Goldman and D. L. Spector. Live Cell Imaging: A Laboratory Manual [M].2nd ed. New York: Cold Spring Harbor Laboratory, 2009.

3 A. Brown. Slow axonal transport, in New Encyclopedia of Neuroscience [M]. L. R.Squire, Ed. Oxford, U.K.: Academic, 2009,1–9.

4 A. Brown. Axonal transport of membranous and non-membranous cargoes:A unified perspective [J]. The Journal of Cell Biology, 2003, 160(6):817–821.

5 R. Perrot, R. Berges, A. Bocquet, and J.Eyer. Review of the multiple aspects of neurofilament functions, and their possible contribution to neurodegeneration [J].Cellular and Molecular Neurobiology, 2008,38(1): 27–65.

6 A. Brown. Slow axonal transport: Stop and go traffic in the axon [J]. Nature Reviews Molecullar Cell Biology, 2000,1(2): 153–156.

7 A. Brown. Axonal transport. In“Neuroscience in the 21st century”, ed. D.W.Pfaff [M], Springer, New York, 2013,255-308.

8 A. Brown and P. Jung. A critical reevaluation of the stationary axonalcytoskeleton hypothesis[J]. Cytoskeleton,2013, 70(1):1-11.

9 E. Meijering, I. Smal, and G. Danuser.Tracking in molecular bioimaging [J]. IEEE Signal Process Magzine, 2006, 23(3):46–53.

10 I. F. Sbalzarini and P. Koumoutsakos.Feature point tracking and trajectory analysis for video imaging in cell biology[J]. Journal of Structural Biology, 2005,151(2): 182–195.

11 J. Zhu and L. Yuan. Neurofilament tracking by detection in fluorescence microscopy images [C], in proceeding of international conference on image processing, 2013, 3123-3127.

12 K. Jaqaman, D. Loerke, M. Mettlen, H.Kuwata, S. Grinstein, S. Schmid, and G.Danuser. Robust single-particle tracking in live-cell time-lapse sequences [J]. Nature Methods, 2008, 5(8): 1212–1221.

13 K. Jaqaman and G. Danuser.Computational image analysis of cellular dynamics: A case study based on particle tracking [J]. Cold Spring Harb Protocal,2009, 2009(12): pdb.top65.

14 G. Yang, A. Matov, and G. Danuser.Reliable tracking of large scale dense antiparallel particle motion for fluorescence live cell imaging [C]. Proceding of IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA,2005: 9–17.

15 M. K. Cheezum,W. F.Walker, andW. H.Guilford. Quantitative comprison of algorithms for tracking single fluorescent particles [J]. Biophysical Jurnal, 2001, 81(4):2378–2388,.

16 B. C. Carter, G. T. Shubeita, and S.P.Gross. Tracking single particles:A user-friendly quantitative evaluation [J].Physical Biology, 2005, 2(1): 60–72,.

17 I. Smal,K.Draegestein, N.Galjart,W.Niessen, and E.Meijering. Particle filtering for multiple object tracking in dynamic fluorescence microscopy images:Application to microtubule growth analysis[J]. IEEE Transacitons on Medical Imaging,2008, 27(6): 789–803.