基于两次丢包策略的主动队列管理算法研究*

谢立春 张春琴

(浙江工业职业技术学院, 浙江 绍兴 312000)

0 前言

随着网络的迅速发展，拥塞现象日益严重，传统机制是利用丢包对源端进行拥塞控制。虽然这种被动式队列管理（Passive Queue Management，PQM）在Internet上得到了广泛的使用，但存在死锁、满队列和全局同步问题。同时，IETF提出主动式队列管理（Active Queue Management，AQM）技术[1,2]，即在队列溢出前进行丢包，使得源端能够及时对拥塞做出反应，避免死锁等现象的发生。目前已经存在大量AQM算法。最早提出的是随机早期检测

（Random Early Detection，RED）[3-6]，其基本思想是通过监控队列的平均长度来探测拥塞，当发现拥塞存在时就随机地丢弃数据包，以此通知源端发生拥塞，使源端在队列溢出前减小拥塞窗口，降低发送速度，从而缓解网络拥塞状况。但是RED算法存在两个主要缺陷：(i) RED对参数设置很敏感，改变参数对性能影响很大；(ii) 随着网络中“流”(Flow)数目的增加，网关的平均队列长度会逐渐增加。

针对这些问题，研究人员提出了改进方法，包括 ARED、SRED和BLUE算法等。它们是根据网络中负载的情况对标记/丢弃概率进行动态调整。ARED算法[7]主要思想是根据网络负载的情况调整最大概率。当平均队列小于最小阈值，就减小最大概率；当平均队列大于最大阈值，就增大最大概率。而 SRED 算法[8,9]通过估计网络中流的个数来调整报文标记/丢弃概率。在SRED中流的个数通过概率统计的方法获得，所以不需要使用“单流信息”。BLUE算法[10-12]是通过链路空闲和缓冲溢出的状况来调整报文标记/丢弃概率。如果缓冲溢出，就增大概率；如果线路空闲，就减小概率。另外，在PI控制器的基础上方面又提出了REM(Random Exponential Marking)[13]、PI[14]和 AVQ(Adaptive Virtual Queue)[15]等。

在上述工作基础上，文章利用两次丢包策略建立主动队列管理算法，即通过比较实际队列长度和等待时间，提出从队列头部以及队中某一位置随机丢弃数据包。同时，仿真实验将TDPQW算法与RED算法、DROP-TAIL算法进行对比，分析了有效数据包个数和RTT公平性等性能情况。

1 主动队列管理算法TDPQW

假设存在一个如图所示的网络结构，An为发送数据包的源节点，C为服务节点，其队长最大阈值为Qmax，实际队长为q。

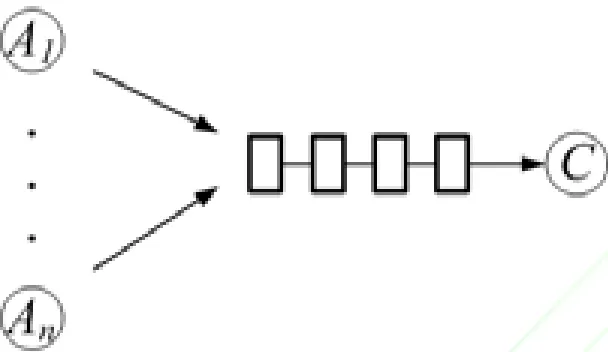
图1 网络仿真结构示意图

网络中经常会出现少数数据流占据大部分带宽，造成死锁现象。并且当具有不同RTT的TCP数据流竞争链路带宽时，RTT较小的TCP数据流的拥塞窗口的增长速度会快于RTT大的TCP数据流，从而占有较多的网络带宽，造成网络传输中的不公平性现象。RFC2309指出死锁是由于网络同步或其它计时作用的结果，从队列头部丢弃数据包使得各数据流发现拥塞不一致，就能打破同步，解除网络死锁。对此，本文采取了两次丢包策略，即从队列头部丢弃一个数据包，以及随机产生[1, Qmax-1]之间的随机值，并丢弃该位置处的数据包。

根据上述思想，这里提出主动管理算法TDPQW（Twice Dropping Packets with Queue length and Waiting time）。TDPQW算法不仅将实际队长q作为判断丢包的依据，而且为了避免某种数据流长时间占用带宽，提出了将实际等待时间w作为另一个判断依据。同时，考虑到实际流量具有自相似特性，所以这里利用小波变换首先对实际流量进行处理，以此减少长相关所带来的影响。具体算法如下所述：

(1) 根据式(1)对达到的数据流采用MALLAT算法进行小波变换，通过减少流量的长相关特性，重新获得重构后的新数据流；

其中，A(j)和D(j)分别为近似系数和小波系数，H为低通滤波器，G为高通滤波器，j为小波分解层次。

(2) 由重构后的新数据流，判断当前队列长度q与队列长度阈值之间的关系，如果q＜Qmin（Qmin为队长最小阈值），则不进行任何丢包处理，该数据流进入队列，重复步骤(2)；否则跳转到步骤(3)；

(3) 如果Qmin＜q＜Qmax，并且w＜Wmax（Wmax为等待时间最大阈值），说明当前网络有轻度拥塞现象，按照概率Pb随机丢弃[1, Qmax-1]中某一位置的数据包，该数据流进入队列，跳转到步骤(1)；否则跳转到步骤(4)；

(4) 如果Qmin＜q＜Qmax，并且w≥Wmax，按照概率Pb首先丢弃队列头部的一个数据包，然后随机丢弃[1, Qmax-1]中某一位置的数据包，该数据流进入队列，跳转到步骤(1)；否则跳转到步骤(5)；

(5) 如果 q≥Qmax，直接丢弃队列头部的一个数据包以及[1, Qmax-1]中某一位置的数据包，该数据流进入队列，跳转到步骤(1)；

(6) 算法结束。

在实际运行中，节点 C的服务率可能因为环境和资源的影响而造成动态变化，所以以下结合M/G/1排队模型来研究实际队长q和等待时间w。

2 实际队长和等待时间的计算

假设系统满足 M/G/1排队模型[16-18]，采用先来先服务的策略。数据包到达时如果服务源空闲就立即服务，否则进行排队等待。服务节点C服务率为µ，数据包平均到达率为p，并且服从一般分布G(t)，则：

令Qt表示t时刻系统到达的数据包，rt表示第t个服务时间段θt到达的数据包个数，{Qt,t≥0}是一个不可约、非齐次MC，易知一步转移概率pk：

其中，k≥0。

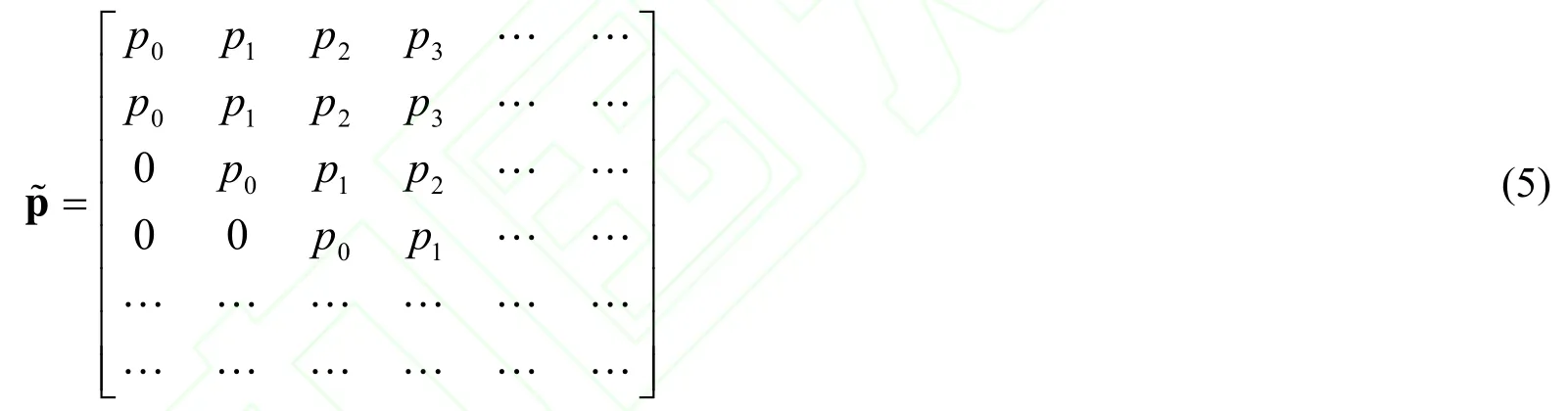
假设P(y)为pk的母函数，当时，是正常返的，存在：

其中，|y|≤1，并且

后续数据包服务时间θn(n=2, 3, 4, …)，并且θn之间相互独立，根据文献[19]，利用全概率公式可得其队列长度q(t)的瞬时分布为：

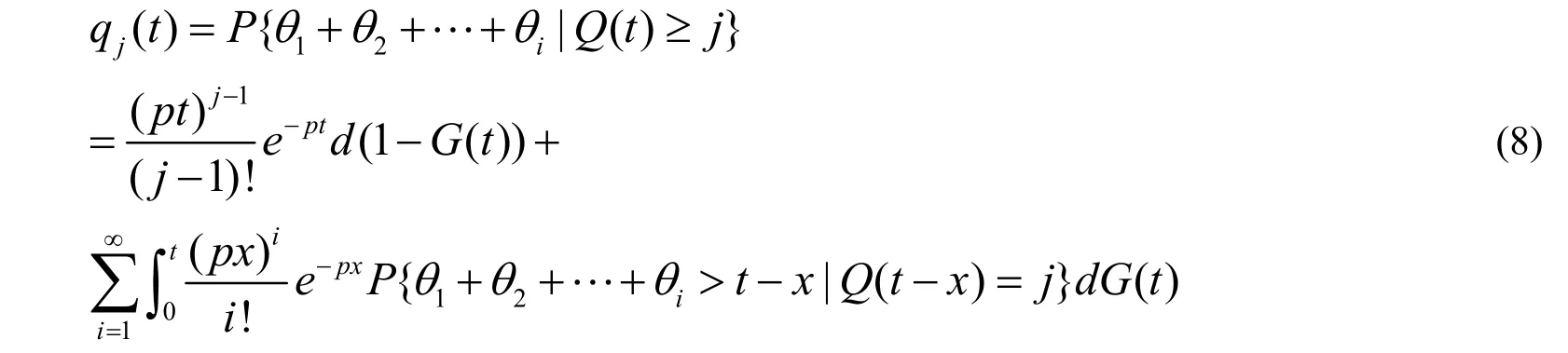
其中，j≥1。

由于队列长度q(t)只与数据包个数有关，则：

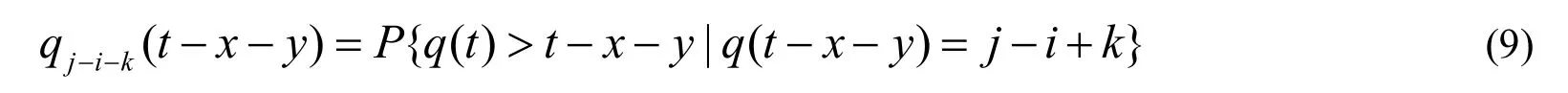
并且结合θn的独立同分布性，有：

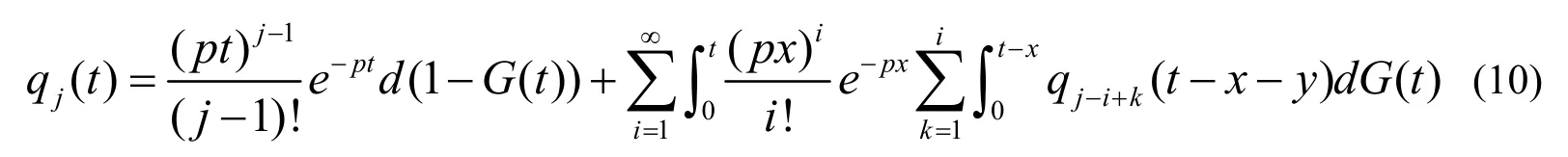
假设W(t)、U(t)分别代表稳态下数据包的等待时间和逗留时间分布，满足：

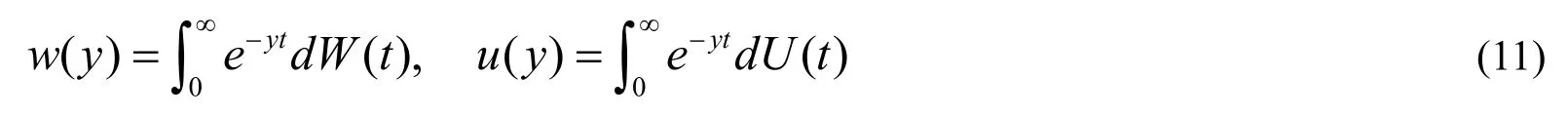
那么在该逗留时间U(t)内到达的数据包个数为[19]：

则：

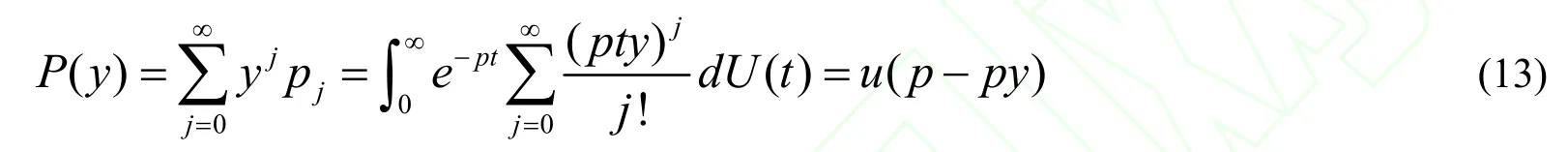
即：

同时由于逗留时间为等待时间与服务时间之和，所以可得实际等待时间：

即：

3 数学仿真

根据上述稳态下的等待时间的计算方法，这里首先假设服务时间服从1/µ的定长分布。根据式(15)，其数据包的等待时间w1可表示为：

在NS2中建立如图1仿真网络拓扑，假设存在3个数据源节点An（n=1, 2, 3），各链路容量为15Mbps，延时20ms，缓存大小为50 packets；节点An均为持久性FTP业务源，采用TCP Newreno协议，数据包均为2000Byte。为了验证TDPQW算法的有效性，这里将RED算法和DROP-TAIL算法进行对比分析。图2显示了在50ms内从节点An到节点C的有效数据包个数。从图中可以看处，DROP-TAIL算法性能较差，而TDPQW算法性能最优。通过数据分析，TDPQW算法比DROP-TAIL算法和RED算法的性能分别提高了10.23%和7.91%。

同时，这里为了验证算法的公平性，节点A1、A2和A3发送数据包的延时分别为10ms、20ms和30ms。图3、图4和图5分别给出了TDPQW算法、RED算法和DROP-TAIL算法RTT公平性情况。从图5可以看出RTT存在不公平情况，在RTT为29ms附近时，其节点A3发送的有效数据包明显超过节点A2，这是由于网络发生死锁现象。而从图3和图4可以看出，TDPQW算法的公平性要优于RED算法。

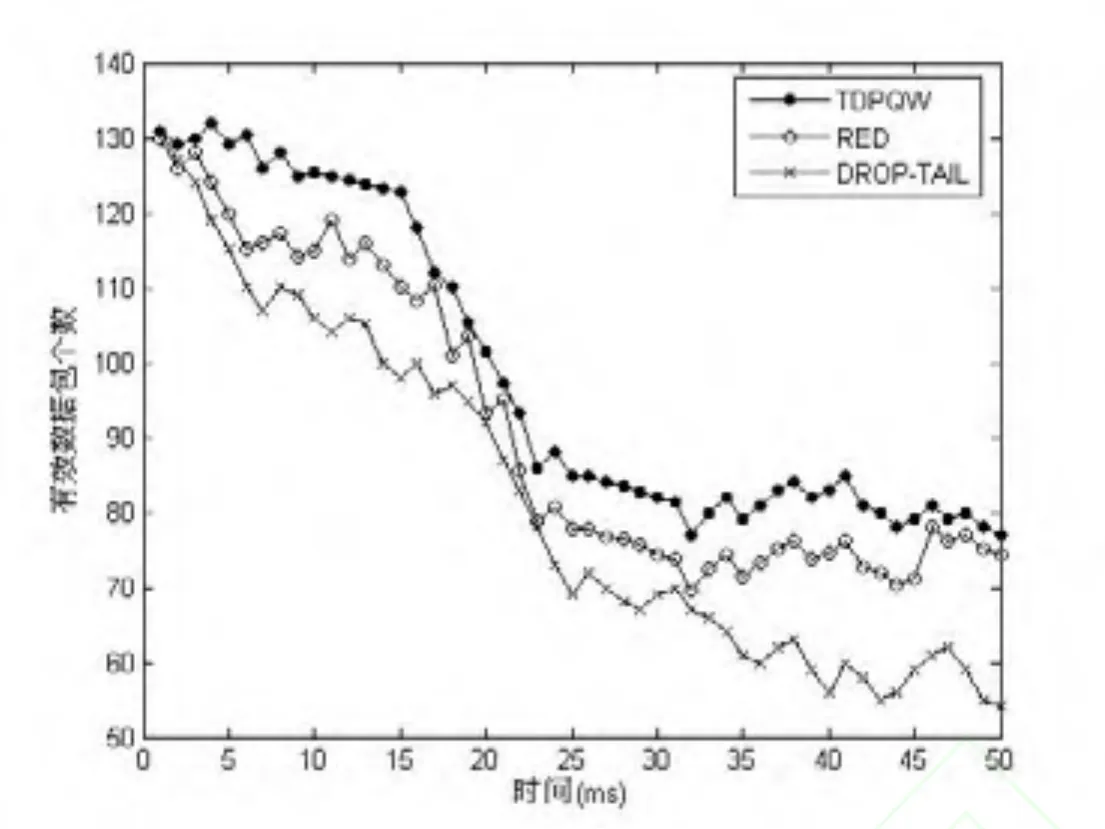
图2 有效数据包个数比较

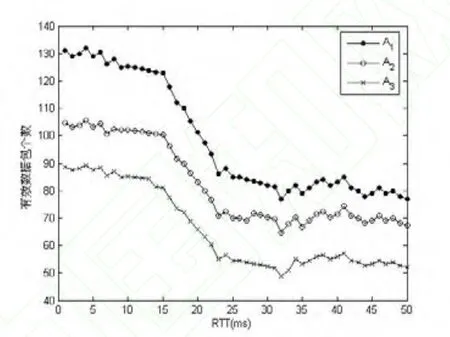
图3 TDPQW算法的RTT公平性

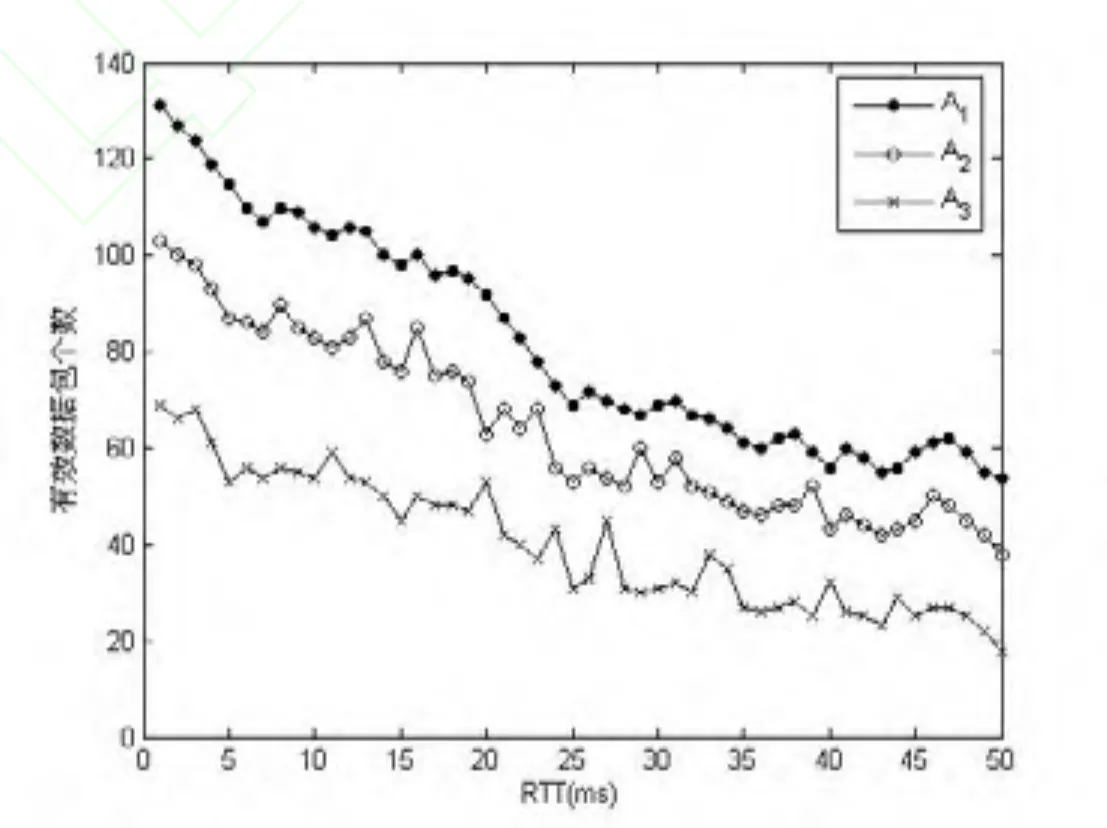
图4 RED算法的RTT公平性

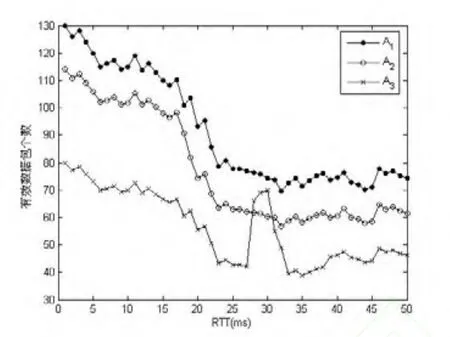
图5 DROP-TAIL算法的RTT公平性

在文献[20]中，提出了一种两次随机丢包的被动队列管理算法DropRand2，这里将TDPQW算法和DropRand2算法进行比较。针对于节点A1，在图6中给出了这两种算法的RTT公平性比较。从图6可以看出，本文提出的TDPQW算法在前期具有一定优势，而在后期劣于DropRand2算法。

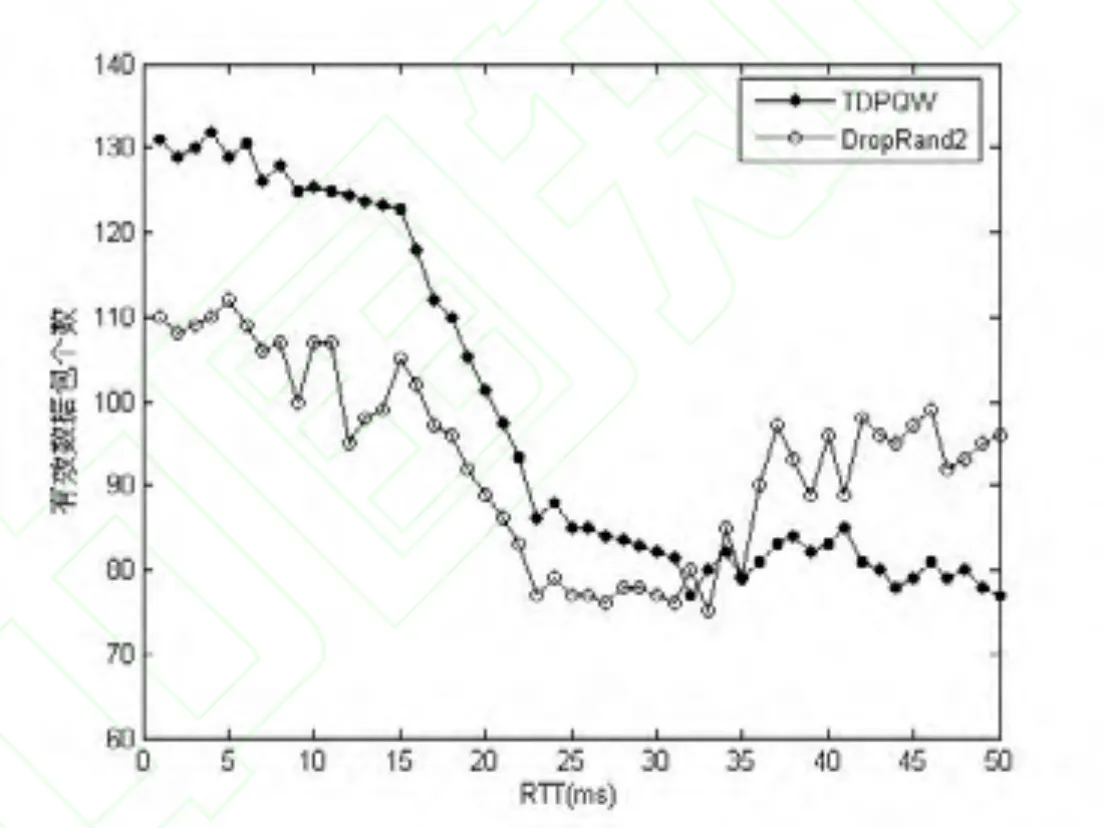
图6 算法TDPQW和DropRand2性能比较

为了深入TDPQW算法中各种影响因素对性能产生的影响，这里假设服务时间服从kµ的k阶Erlang分布，其数据包等待时间w2可表示为：

根据式(16)和式(17)得到两种分布下数据包的等待时间与服务率之间的关系，如图7所示。从图7可以看出，整体趋势上随着服务率的增加数据包的等待时间是随之减小，直至平稳状态。但是当处于相当服务率下时，k阶Erlang分布比定长分布下降的速度更快，这说明k阶Erlang分布下的数据包等待时间更短，也即是意味着要获得相同的等待时间，定长分布下所要求系统的服务率更高，此时采用k阶Erlang分布能够获得更好的性能。

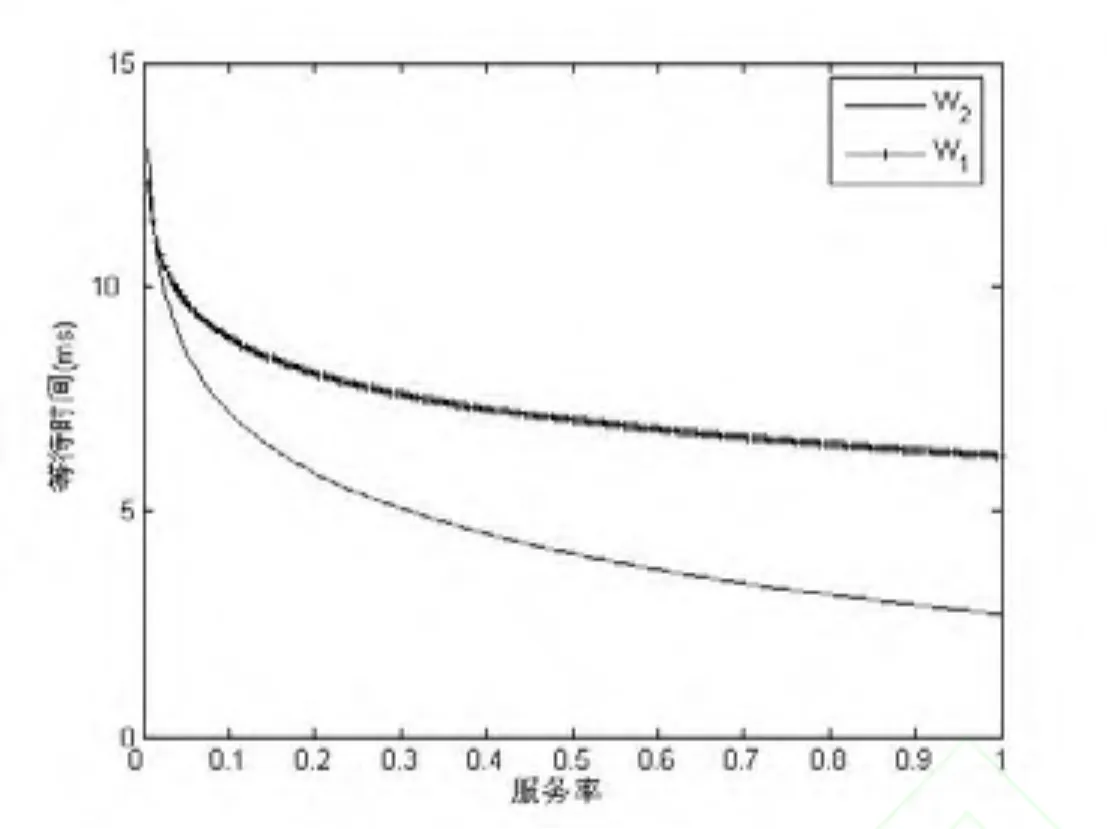
图7 等待时间与服务率之间关系

4 结论

针对队列管理中的死锁和公平性问题，本文采取两次丢包策略建立了主动队列管理算法TDPQW。通过比较实际队列长度和等待时间，提出从队列头部以及[1, Qmax-1]中的某一位置随机丢弃数据包。同时，以M/G/1排队模型推导了实际队列长度和等待时间的数学表达式。最后仿真实验将TDPQW算法与RED算法、DROP-TAIL算法、DropRand2算法进行对比，深入分析了有效数据包个数和RTT公平性情况，结果表明TDPQW算法的性能更优。在后续研究中，可考虑结合REM、PI控制器等建立一套完善的队列管理模型。

[1]吴春明, 姜明, 朱淼良. 几种主动式队列管理算法的比较研究[J]. 电子学报, 2004, 32(3):429-434.

[2]黄磊, 吴春明, 姜明, 张栋. REDu: 一种新的识别并惩罚非适应流的主动式队列管理算法[J]. 电子学报, 2010, 38(8): 1759-1762.

[3]S. Floyd, V. Jacobson. Random early detection gateways for congestion avoidance[J].IEEE/ACM Transactions on Networking, 1993, 1(4): 397-413.

[4]W. Zhang, L. Tan, G. Peng. Dynamic queue level control of TCP/RED systems in AQM routers[J]. Computers & Electrical Engineering, 2009, 35(1): 59-70.

[5]M. Christiansen, K. Jeffay, D. Ott, F. D. Smith. Tuning RED for Web Traffic[J]. ACM Computer Communication Review, 2000, 30(4): 139-150.

[6]S. Liu, T. Basar, R. Srikant. Exponential-RED: a stabilizing AQM scheme for low-and high-speed TCP protocols[J]. IEEE/ACM Transactions on Networking, 2005, 13(5):1068-1081.

[7]W. Chen, S. H. Yang. The mechanism of adapting RED parameters to TCP traffic[J].Computer Communications, 2009, 32(13): 1525-1530.

[8]Feng-yuan Ren, Chuang Lin, Fu-bao Wang. Stability of RED algorithm: analysis based on nonlinear control theory[J]. Chinese Journal of Computers, 2002, 25(12): 1302-1307.

[9]T. J. Ott, T. V. Lakshman, L. H. Wong. SRED: Stabilized RED[C]. In Proceedings of IEEE INFOCOM, New York, USA: IEEE Communications Society, 1999: 1346-1355.

[10]Wu-chang Feng, K. G. Shin, D. D. Kandlur, et a1. The BLUE active queue management algorithms[J]. IEEE/ACM Trans. on Networking, 2002, 10(4): 513-528.

[11]吴春明, 姜明. SBlue: 一种增强Blue稳定性的主动式队列管理算法[J]. 通信学报, 2005,26(3): 68-74.

[12]刘伟彦, 孙雁飞, 张顺颐, 等. 一种参数自适应的主动队列管理算法——自适应BLUE[J]. 电子与信息学报, 2009, 31(2): 442-446.

[13]S. Athuraliya, V. H. Li, S. H. Low, Q. Yin. REM: Active queue management[J]. IEEE Network, 2001, 15(3): 48-53.

[14]钱艳平, 李奇. 大时滞网络自适应预测 PI主动队列管理算法[J]. 控制与决策, 2006,21(8): 937-940.

[15]S. Kunniyur, R. Srikant. Analysis and design of an adaptive virtual queue (AVQ) algorithm for active queue management[J]. ACM Computer Communication Review, 2001, 31(4):123-134.

[16]Kim B.. Tail asymptotics for the queue size distribution in a discrete-time Geo/G/1 retrial queue [J]. Queueing System, 2009, 61: 243-254.

[17]朱翼隽, 冯艳刚, 周宗好. 具有Bernoulli反馈的负顾客M/G/1休假排队系统[J]. 工程数学学报, 2009, 26(2): 369-372.

[18]Tian N., Zhao X., Wang K. The M/M/1 queue with single working vacation[J]. Journal of Information and Management Sciences, 2009, 19: 621-634.

[19]唐应辉, 唐小我. 排队论[M]. 科学出版社, 2006.

[20]姜文刚, 孙金生, 王执铨. 两次随机丢包的被动队列管理算法[J]. 系统仿真学报, 2011,23(5): 987-997.