结合PCA与HEIV的椭圆目标检测算法

韩建栋，温 静

HAN Jiandong,WEN Jing

山西大学 计算机与信息技术学院，计算智能与中文信息处理教育部重点实验室，太原 030006

School of Computer and Information Technology,Key Laboratory of Ministry of Education for Computational Intelligence and Chinese Information Processing,Shanxi University,Taiyuan 030006,China

椭圆是计算机视觉中常见的图像特征，在众多计算机视觉应用中，都需要对椭圆进行检测，如生物医学中细胞显微图像的自动判读、工业生产中圆形产品自动检测、视觉测量中人造圆形标志点的精确定位等。因此，椭圆检测在基于图像的识别与测量领域中具有非常重要的意义。

任意椭圆具有5个参数，椭圆检测就是对椭圆进行识别并确定椭圆的5个参数。目前常见的椭圆检测算法主要有：Hough变换法与曲线拟合法。传统的Hough变换[1]将图像空间映射到五维参数空间进行统计，计算效率很低。为此，Xu等[2]提出了随机Hough变换法，通过随机抽取5个点计算椭圆参数，降低了计算量，但是当边缘点数较大时，该方法由于无目标地随机采样会引入大量的无效计算，导致算法性能降低[3]，为了进一步克服Hough变换对时空需求高的缺点，提出各种一维Hough的椭圆检测算法[4-8]，如Xie[4]等提出利用椭圆长轴的两个顶点与椭圆上另外一点来确定椭圆参数的方法，该方法仅需要一个一维累加器来统计短轴长度信息，降低了检测的复杂度，但是检测精度较低。曲线拟合法是事先知道待测目标为椭圆的前提下，根据测量得到的边缘点坐标估计椭圆的参数，如最小二乘拟合法[9-11]、基于RANSAC的椭圆检测法[12-13]等。

在机器视觉测量中，常常需要对自然场景中的人造椭圆目标进行识别与精确定位，而自然场景中往往存在众多干扰目标。因此，在采用椭圆定位之前有必要剔除场景中的非椭圆及近似椭圆目标。考虑到椭圆长轴对应于椭圆主元方向的特点，本文提出一种基于主元变换法的椭圆自动识别方法，利用主元变换将任意椭圆转化为标准型椭圆，将椭圆轮廓度误差作为识别椭圆的评价依据，并考虑数据的异方差性，实现椭圆目标的精确定位，该方法简化了椭圆检测过程，且具有较高的定位精度。

1 主元变换及其特点

主元变换法[14]（Principal Components Transform）是一种基于图像统计特性的变换，又称特征值变换或离散KL变换。

由图像样值序列组成的N个随机采样矢量 X=[x1，x2，…，xN]T，其均值矢量与协方差矩阵可以近似表示为：

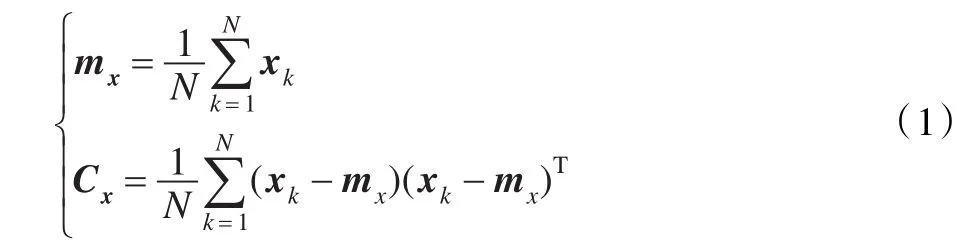
其中，协方差矩阵Cx是一个实对称矩阵，总能找到一组（N个）正交特征矢量 ei与特征值λi(i=1，2，…，N)，由降序排列的特征值所对应的特征矢量组成正交变换矩阵A。将随机采样数据X经过变换A转换为序列矢量Y：

式（2）称为主元变换。从几何观点来看，主元变换其实质是提取协方差矩阵的特征矢量作为主元方向，建立一个以图像坐标原点为原点，主元方向为坐标轴的主轴坐标系，将数据X进行旋转变换，将其主轴沿着主元方向对齐。

由于椭圆的长轴方向对应于椭圆的主元方向，因此，对椭圆的边缘数据经过主元变换，可以将任意方向的椭圆转化为标准型椭圆，有利于椭圆目标的识别与定位。如图1所示，其中，x-y为原图像坐标系，e1-e2为变换后的主轴坐标系。

图1 主元变换示意图

2 基于主元变换的椭圆检测方法

2.1 图像预处理

众多边缘检测的方法中，坎尼算子[15]具有低误码率、高定位精度和抑制虚假边缘等优点。其基本思想是：选择高斯滤波器对图像进行平滑滤波，采用“非极值抑制”方法对平滑后的图像进行处理，通过双阈值门限法得到所需要的单像素边缘图像。

为了对目标进行形状分析，还需要采用轮廓跟踪技术寻找目标边缘点，将目标边缘点连成一条连续的边界。

2.2 椭圆识别方法

基于主元变换的椭圆识别法步骤为：

（1）计算目标边缘点集X的均值矢量mx与协方差矩阵Cx。

（2）对协方差矩阵Cx进行奇异值分解，将特征值按降序排列，对应的特征矢量ei作为变换矩阵A的行向量。

（3）按照式（2）将边缘点集 X转换到主轴坐标系，生成新的边缘点集Y。若该点集是椭圆目标的边缘，在理想情况下，Y应为标准型椭圆边缘数据：

其中，(x，y)为点集Y 中的边缘点坐标，参数 (x0，y0，a，b)分别为椭圆中心坐标、长半轴与短半轴，可以通过求取点集Y中水平轴与垂直轴取值范围来获取：

（4）由于图像的数字化处理，椭圆边缘点集Y并不完全满足标准型方程，定义点集Y中数据点与标准椭圆轮廓Y′的平均最短距离作为椭圆轮廓度误差判据：

利用式（5）计算任意点距离标准椭圆轮廓的最短距离时，需要进行局部寻找[16]，当边缘点数较大时计算量较大。若将标准椭圆看作是由标准圆（中心坐标（0，0），半径为b）经过中心投影得到的，将数据点集Y进行变换：

其中：

则数据点集Z与标准圆轮廓的接近程度可以表征数据Y与标准椭圆轮廓的接近程度。计算点集Z中任意点(z1，z2)距离标准圆轮廓的最短距离，重新定义椭圆轮廓度误差函数：

（5）设定阈值T，满足J2＜T的点集Y（或对应的 X）为椭圆目标边界。通常，阈值T取0.5＜T＜1。

2.3 椭圆中心定位

在现代工业测量领域，要求具有高精度亚像素级的定位精度，由式（4）得到的椭圆参数不能满足精度要求。为了进一步提高定位精度，采用异方差的变量含误差模型进行椭圆拟合。

椭圆曲线一般方程为：

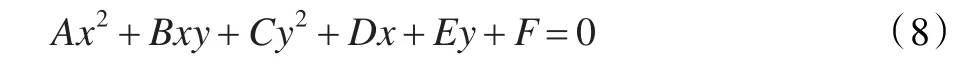
令 x=(x，y)，Z(x)=[x2，xy，y2，x，y]，α=F，β=[A，B，C，D，E]，式（8）可表示为：

考虑二阶近似，得到数据 Z(xi)的噪声δZi的均值与协方差矩阵为[17-18]：

从上式可知，噪声δZi不是独立同分布的，将噪声数据Zi与真值数据Zio之间的马氏距离作为价值函数：

令 ∂J1/∂s=0 ，s=α，β，Zi，将问题转化为求解广义特征向量（GSVD）问题[18]，通过迭代进行求解。至此，椭圆的5个参数完全确定。

3 实验

对本文提出的基于PCA变换的椭圆识别算法进行数字仿真，并通过拍摄实际场景图像来验证本文算法的有效性。

3.1 椭圆识别仿真实验

对椭圆识别算法进行计算机仿真，如图2所示，图2（a）为待检测的图像，图2（b）为提取的边缘图像，对每组边缘数据进行主元变换，结果如图2（c）所示。从图可知，主元变换将任意椭圆转化为标准椭圆。计算各种图形的椭圆轮廓度误差，分别为（0.2749，0.2888，0.1929，6.9435，2.7926，2.1022），设定阈值 T=1，很容易识别出椭圆目标。

图2 椭圆识别仿真图像

3.2 实际场景的椭圆识别与定位实验

实验中，采用尼康D100单反相机拍摄一幅航天器薄膜充气可展开天线图像，图像分辨率为3008 pixel×2000 pixel，包含约140个待求目标点，如图3所示。由于天线表面对摄像机闪光灯光源的反射以及拍摄角度的原因，所采集的图像中既包含大片形状不规则的亮斑，又有极小的亮点，甚至会有一些非椭圆目标存在，利用面积阈值可以很容易剔除极小亮点。而对于一些形状不规则的非椭圆目标，若不事先进行椭圆识别，必然对天线面型拟合造成很大的误差，而采用本文提出的基于PCA变换的椭圆识别算法，通过求取椭圆轮廓度误差可以很方便剔除非椭圆目标，如图3所示，检测出的非椭圆目标已用矩形框标注。

图3 薄膜充气式可展开天线试验场

对实际拍摄的另一幅试验场图像进行椭圆检测，如图4所示，试验场布置了25个具有回光反射标志的圆形标志点，摄像机从某一站位进行拍摄，截取部分图像，大小为695 pixel×554 pixel，所有目标边缘点数在40～50个像素之间。采用本文方法与最小二乘拟合法进行椭圆检测，表1列出了部分椭圆目标的椭圆轮廓度误差以及中心坐标（保留两位有效数字）。所有椭圆目标的椭圆轮廓度误差均位于0.4 pixel以下，比较两种方法定位中心的偏差，本次实验中，最大偏差为0.108 pixel，偏差均值为0.056 pixel。

图4 试验场图像

表1 试验场部分椭圆中心检测结果 pixel

4 结束语

椭圆识别与定位是计算机视觉中关键技术之一。将主元变换法应用于椭圆检测，给出一种新的椭圆轮廓度误差评价方法。首先提取边缘数据的主元方向，将任意椭圆转换为标准型椭圆，利用椭圆轮廓度误差进行椭圆识别，并考虑数据的异方差特性，采用异方差的变量含误差模型实现椭圆目标的精确定位。实验证明，该方法可实现椭圆目标的自动识别，在噪声方差为σ2=0.05情况下，定位精度小于0.04 pixel，在椭圆目标识别及视觉测量领域具有广泛的应用前景。

[1]Hough P V C.Method and means for recognizing complex patterns：USA，3069654[P].1962.

[2]Xu L，Oja E，Kultaned P.A new curve detection method：Randomized Hough Transform（RHT）[J].Pattern Recognition Letter，1990，11（5）：33l-338.

[3]于海滨，刘济林.基于中心提取的RHT在椭圆检测中的应用[J].计算机辅助设计与图形学学报，2007，19（9）：1107-1113.

[4]Xie Y H，Ji Q.A new efficient ellipse detection method[C]//16th International Conference on Pattern Recognition，Los Alamitos，2002：957-960.

[5]祝建中.基于中心估计的椭圆检测[J].计算机工程与应用，2008，44（4）：65-67.

[6]于海滨，刘敬彪，刘圆圆.基于对称点搜索的一维RHT在椭圆检测中的应用[J].电子与信息学报，2009，31（8）：1830-1834.

[7]霍天欢，陈临强.基于一维Hough变换的椭圆检测改进算法[J].杭州电子科技大学学报，2011，31（2）：54-57.

[8]王长元，张景，李京京.瞳孔中心快速定位方法研究[J].计算机工程与应用，2011，47（24）：196-198.

[9]Halíř R，Flusser J.Numerically stable direct least squares fitting of the ellipses[C]//Processings of the 6th International Conference in Central Europe on Computer Graphics，Visualization and Interactive Digital Media，1998：125-132.

[10]安新源，周宗潭，胡德文.椭圆拟合的非线性最小二乘方法[J].计算机工程与应用，2009，45（18）：188-190.

[11]邹益民，汪渤.一种基于最小二乘的不完整椭圆拟合算法[J].仪器仪表学报，2006，27（7）：808-812.

[12]张文聪，李斌，邓宏平，等.视线跟踪过程中变形瞳孔的定位[J].电子与信息学报，2010（2）：416-421.

[13]魏凌，曾滔，陆艳华，等.一种用于光焦度计的椭圆中心快速计算方法[J].光电工程，2012（12）：26-31.

[14]章毓晋.图像处理[M].2版.北京：清华大学出版社，2006：265-267.

[15]Canny J.A computational approach to edge detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1986，PAMI-8（6）：679-698.

[16]黄凤山，王春梅.光笔式视觉坐标测量中控制点光斑图像的识别[J].光学精密工程，2007，15（4）：587-591.

[17]Matei B，Meer P.A general method for errors-in-variables problems in computer vision[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition（CVPR’00），2000，2：18-25.

[18]Matei B.Heteroscedastic Error-in-Variables models in computer vision[D].Department of Electrical and Computer Engineering，Rutgers University，2001.