基于灰信息变元的泛函博弈模型研究
,, ,,
(南京航空航天大学经济与管理学院,江苏 南京 211106)
1 引言
自冯·诺依曼和摩根斯坦恩合作出版《博弈论和经济行为》以来,博弈理论得到不断发展,已成为一门较为成熟、应用广泛的学科。学者们各自从不同的角度,例如完全信息、不完全信息、静态、动态等研究了博弈论,使其逐步完善。近年来,随着不确定性理论研究的深入,学者们尝试在博弈研究中考虑不确定性因素。概括来说,不确定博弈模型主要有以下几个研究方向。灰色不确定性博弈:罗党,吴顺祥[1]提出了二人有限零和灰色博弈,建立了博弈平衡解优序关系的确定方法。方志耕等[2]研究了基于纯策略的灰矩阵二人有限零和最保守博弈决策问题,提出了该问题解的灰鞍点概念。倪健等[3]基于灰色思想和博弈理论分析高速公路入口冲突车辆受到的不确定性因素,提出冲突车辆选择策略时受到区间灰数的约束,建立冲突车辆的零和灰色博弈模型。随机不确性博弈:Hoppe[4]分析了不确定条件下采用新技术的期权博弈模型。黄学军等[5]假定突发事件服从向下的泊松跳过程,建立了带跳的几何布朗运动的双寡头期权博弈模型。王皓[6]主要研究了倒向随机微分方程解的存在性、唯一性,及其在混合零和微分-积分对策问题上的应用。已知参数变化范围的不确定性博弈。Capisani等[7]结合经典Nash均衡及帕雷托有效解的概念,介绍了不确定性下非合作博弈的NS-均衡概念。Nikobin等[8]在Zhukovskii的基础上定义了不确定环境下非合作博弈的ZS-均衡概念,并基于不动点定理证明了其存在性。张会娟等[9]在已知不确定参数变化范围的假设下,定义并研究了具有不确定参数的强Nash均衡的存在性问题。模糊不确定性博弈。认知的不确定性,人们可能遇到收益值为模糊数的博弈结构。针对此问题,吴诗辉等依据三角模糊数的运算规则和比较规则,提出了三角模糊矩阵博弈问题的基于可能度的纯策略解的判定规则[10]。岳立柱等[11]文献利用结构元相关定理,证明了m×n阶模糊矩阵必存在与之有相同纳什解的m×n阶实数矩阵与其对应,并用结构元方法简化了模糊博弈矩阵的求解。
综合来看,不确定性信息下的博弈问题研究已经得到学术界的重视,取得一些有意义的研究成果。但是,仍有部分问题值得深入研究:(1)现有不确定性博弈多数考虑收益值为灰数、已知变化范围的参数、模糊数等情况,未能考虑到参与人的收益值虽无法准确获知,却往往与动态环境因素有着密切关联这种情况。(2)对于博弈中局中人的博弈策略或收益值是某些条件或变元(如时间、环境、空间、制度或相关其它变元)的映射的这一类博弈问题,目前暂没有比较有效的模型描述。(3)以往多数研究只能给出一定程度上的静态均衡解,事实上随着博弈环境的不同,博弈均衡解会动态变化。
在现实的社会生活中,在信息不确定条件下的博弈问题,局中人的博弈策略或收益值往往无法在事先准确给定。分析基于不确定信息的泛函博弈问题,并描述其形式与框架,构建相应的博弈模型,可以准确的表达现实世界中的博弈问题,可以展示不确定信息下博弈的特征、性质、战略表达形式等,为模型最优策略探讨及均衡解的研究打下坚实的基础。本文重点研究和描述基于不确定性的变元和收益值取决于博弈策略变元的泛函博弈的战略式(标准表达形式),构建的博弈模型将为更好地认知、把握和解决现实博弈问题提供新的科学依据。
2 泛函区间灰数表征形式及运算法则
针对在现实的社会经济生活中,大量存在着基于不确定信息的问题,即在信息不确定条件下,我们所得到的信息可能是某些条件或变元(如时间、环境、空间、制度或相关其它变元)的映射,在标准区间数[15]的基础上设计一种新的基于信息不确定性变元的泛函区间灰数,为解决这些信息缺失环境下不确定性变元泛函区间灰数的运算问题奠定基础。
γi(t)=F[f1(t),f2(t),…fK(t)],γi(t)∈[0,1],i=1,2,…
(1)
尽管这些变元函数γi(t)∈[0,1];i=1,2,…映射的确切规律难以准确把握,但是若在一定的条件,随着时间的推移,利用相关的统计数据、知识和经验等,能够对其相关的映射规律进行更深入地分析(值得注意的是,变元函数γi(t)∈[0,1]中的t是一种广义时间的表述方式,其所表达真正含义是随着时间的推移,其不确定信息不断变得更加清楚、准确),所以可以将不确定信息的标准区间数转化为一种依托于变元函数γi(t)∈[0,1];i=1,2,…的泛函区间灰数集,如式(2)的形式:
(2)
定义2 (泛函区间灰数的取值) 任给某泛函区间灰数Ai(t)=ai+ci·γi(t);i=1,2,…,若随着时间的推移,利用相关的统计数据、知识和经验等对其不确定性变元函数γi(t)∈[0,1]取定某一确定的值,即γi(t)=γi,(0γi1),那么Ai的值即可唯一确定,则称γi1)为Ai的取数。
法则1 (泛函区间数的加法) 设:
Ai(t)=ai+ci·γi(t);γi(t)∈[0,1],i=1,2,…
Aj(t)=aj+cj·γj(t);γj(t)∈[0,1],j=1,2,…
则Ai(t)与Aj(t)的和记为:
Ai(t)+Aj(t)=[(ai+aj),(ci·γi(t)+cj·γj(t))],i,j=1,2,…
法则2 (泛函区间数的减法) 设:
Ai(t)=ai+ci·γi(t);γi(t)∈[0,1],i=1,2,…
Aj(t)=aj+cj·γj(t);γj(t)∈[0,1],j=1,2,…
则Ai(t)与Aj(t)的差记为:
Ai(t)-Aj(t)=[(ai-aj),(ci·γi(t)-cj·γj(t))],i,j=1,2,…
法则3 (泛函区间数的乘法) 设:
Ai(t)=ai+ci·γi(t);γi(t)∈[0,1],i=1,2,…
Aj(t)=aj+cj·γj(t);γj(t)∈[0,1],j=1,2,…
则Ai(t)与Aj(t)的积记为:
Ai(t)·Aj(t)=[min{(ai·aj),(ai·cj·γj(t)),(ci·γi(t)·cj·γj(t)),(ci·γi(t)·aj)},max{(ai·aj),(ai·cj·γj(t)),(ci·γi(t)·cj·γj(t)),(ci·γi(t)·aj)}],i,j=1,2,…
法则4 (泛函区间数的除法) 设:
Ai(t)=ai+ci·γi(t),γi(t)∈[0,1],i=1,2,…
Aj(t)=aj+cj·γj(t),γj(t)∈[0,1],j=1,2,…
则Ai(t)与Aj(t)的商记为:
Ai(t)/Aj(t)=[min{(ai/aj),(ai/[cj·γj(t)]),([ci·γi(t)]/[cj·γj(t)]),([ci·γi(t)]/aj)},max{(ai/aj),(ai/[cj·γj(t)]),([ci·γi(t)]/[cj·γj(t)]),([ci·γi(t)]/aj)}],i,j=1,2,…
定义3 (泛函区间灰数的数域) 设R(•)为一泛函区间灰数集合,若对任意的Ai(t),Aj(t)∈R(•),有Ai(t)+Aj(t),Ai(t)-Aj(t),Ai(t)·Aj(t),Ai(t)/Aj(t)均属于R(•)(商运算时,要满足aj+cj·γj(t)≠0,j=1,2,…),则称R(•)为一泛函区间灰数域。
定义4 (泛函区间灰数的大小比较规则)任给两个泛函区间灰数Ai(t)=ai+ci·γi(t),γi(t)∈[0,1],i=1,2,…
Aj(t)=aj+cj·γj(t),γj(t)∈[0,1],j=1,2,…若满足:
(1)若Ai(t)-Aj(t)≥0,则Ai(t)≥Aj(t);
(2)若Ai(t)-Aj(t)<0,则Ai(t) 定理1 (Ai(t) 本定理的证明过程简单,证明过程省略。 定理2 (Ai(t)=Aj(t)的判定) 任给两个泛函区间灰数Ai(t)=ai+ci·γi(t),γi(t)∈[0,1],i=1,2,…和Aj(t)=aj+cj·γj(t),γj(t)∈[0,1],j=1,2,…;当ai=aj,ci·γi(t)=cj·γj(t),则Ai(t)=Aj(t)。 本定理的证明过程简单,证明过程省略。 在泛函博弈问题中,其不确定性变元主要体现在收益矩阵中,即在其收益值矩阵的相关元素中存在信息不确定性变元和策略不确定性变元。由于这些不确定变元的存在,使得运用经典的博弈求解方法求解泛函博弈问题变得十分困难。运用优化理论及其相关技术方法,设计基于不确定信息的泛函博弈模型及其把泛函博弈问题转化为优化问题的求解方法,即通过研究和构造泛函博弈收益值的广义满秩扩充方阵分析其最优博弈策略和博弈收益值问题,不仅为现实生活中的不确定信息问题提供新的解题思路,更为实际问题的解决提供新的方法参考。 对于难以用准确的白数来表示的局中人各策略的博弈值,可以用一个区间灰数来表示,我们把由这样的区间灰数所构成的博弈损益值矩阵称为灰损益值矩阵A(⊗),如公式(3)所示: (3) 定义5 (灰博弈)局中人1的策略集为S1={α1,α2,…,αm},局中人 2 的策略集为S2={β1,β2,…,βn},局中人事先判断的用区间灰数表征的灰损益值矩阵为A(⊗),称由灰损益值矩阵所决定的博弈问题称为灰博弈,记为G(⊗)={S1,S2,A(⊗)}。 在现实的社会经济生活中,选取信息不确定条件下的一些博弈问题(考虑在一个相对封闭的市场区域内有2家彩电生产商进行市场份额的竞争、战斗机群的空中搏斗、无人机对敌机的跟踪与侦察等),他们的博弈形式可以用进行描述(见公式(4))。 (4) 其中:αi,i=1,2,…,m表示局中人甲的策略;βj,j=1,2,…,n表示局中人乙的策略;[aij,bij],i=1,2,…,m,j=1,2,…,n表示在信息不确定条件下局中人甲和乙分别采取策略αi,i=1,2,…,m和βj,j=1,2,…,n时的博弈收益值的区间灰数;利用标准区间灰数的表征方法,可将其博弈收益值的区间灰数转化为标准形式: [aij,bij)=aij+(bij-aij)·γij,γij∈[0,1],i=1,2,…,m;j=1,2,…,n (5) 更进一步考虑,γij∈[0,1]是由于事先的信息的不确定性(如信息的不对称性、有限知识、随机振荡等变元因素所造成的)所导致的,也就是说,该γij∈[0,1]应是这些变元的一个映射,可表示为式(6)的形式,其中fk(t),k=1,2,…,K表示这K个影响变元是时间t的映射,K和f表示其相应的映射关系。 γij(t)=F[f1(t),f2(t),…,fK(t)],γij(t)∈[0,1],i=1,2,…,m;j=1,2,…,n (6) (7) 考虑可能存在一种博弈其收益值矩阵中的某些元素值的大小取决于局中人采用该策略的频率(或混合策略的值),如考虑博弈的局中人甲采用策略αi,i=1,2,…,m的频率为xi∈[0,1],i=1,2,…,m;局中人乙采用策略βj,j=1,2,…,n频率为yj∈[0,1],j=1,2,…,n而在其博弈收益值矩阵中存在某个(些)元素的值(如式(8)所示),其中:xi(t)∈[0,1],i=1,2,…,m和yj(t)∈[0,1],j=1,2,…,n分别表示其博弈策略xi(t)∈[0,1],i=1,2,…,m和yj(t)∈[0,1],j=1,2,…,n分别是变元t的函数;cij(t),i=1,2,…,m;j=1,2,…,n是博弈收益值矩阵的元素,xi(t)∈[0,1] 和yj(t)∈[0,1]的映射,Fij(i=1,2,…,m;j=1,2,…,n)表示其映射关系。 cij(t)=Fij[xi(t),yj(t)];xi(t)∈[0,1],i=1,2,…,m;yj(t)∈[0,1],j=1,2,…,n (8) (9) 若在泛函区间灰数大小意义下存在纯策略xi*(t),yj*(t),构成局势(xi*(t),yj*(t))使得式(10)成立: (10) cij*(t)ci*j*(t)ci*j(t) (11) 证明:先证明充分性,由于对任意的i,j均有cij*(t)ci*j*(t)ci*j(t),故: (12) 另一方面,对任给i,j,有: (13) 由(12)式和(13)式有: 现在来证明必要性。 设有i*,j*使得: 所以对任意i,j有: cij*(t)ci*j*(t) 证毕。 (14) 运用提供的信息不确定性变元泛函区间灰数的表征与计算方法,并由题意知:a11=γ11(t),a12=2+γ12(t),a21=4,a22=2,盗版者选择盗版、不盗版策略的泛函最优纯策略如式(15)和式(16)。 (15) (16) 图1 盗版企业的最优纯策略仿真图 盗版打击部门者选择不打击、打击策略的最优灰混合策略如式(17)、式(18)。 (17) (18) 图2 局中人2的最优混合策略仿真图 由图1和图2看出,随着时间的推移,盗版打击部门会倾向选择打击策略,但是盗版企业选择盗版、不盗版的概率仍交替增减,这主要是收到灰信息变元的影响。 (19) 图3 最优灰博弈值仿真图 泛函博弈问题的泛函区间灰数计算结果如表1所示,标准区间数计算方法的计算结果是一个区间的数值,尽管最终的取值范围都是相同的,但是上述的基于灰信息变元的泛函博弈问题的计算结果是随时间t不断变化的,是时间t的映射,可以通过计算机仿真的方式确定在某时间范围内博弈的双方都是采取什么策略,而不只是简单的去计算双方策略的范围,给出相对静态的结果。 表1 泛函区间灰数计算结果 本文着眼于在不确定条件下,现实的社会经济生活中局中人的博弈策略或收益值无法准确实现给定的博弈问题,着重于不确定信息的泛函博弈模型的构建与解析,运用和创新经典博弈理论研究方法,还需要深入研究基于不确定信息的泛函博弈的形式与框架、均衡解的求解方法以及泛函博弈模型稳定性等一系列问题,寻求解决此类问题的科学理论和方法。借助于泛函原理构建泛函博弈模型,创新和发展博弈论研究方法;从实践领域来看,本文立足于现实社会经济生活中的相关实际问题为背景,选择具有较好的代表性的泛函博弈的典型案例如“盗版与打击盗版”问题通过计算机仿真对其博弈均衡结果进行详细的对比分析,说明了本文提出的基于信息不确定性变元的区间数的表征及其运算法则的科学性和计算结果的精确性。此外还可以解决“追捕—格斗”、“航迹规划” 等泛函博弈问题。 参考文献: [1] 罗党,吴顺祥.带有灰色约束的二人有限零和博弈研究[J].厦门大学学报(自然科学版),2006,45(1):29-32. [2] 方志耕,刘思峰.基于纯策略的灰矩阵二人有限零和博弈模型研究[J].南京航空航天大学学报,2003,35(4):441-445. [3] 倪健,韩直,彭金栓.基于零和灰色博弈模型的高速公路入口车辆冲突研究[J].公路交通技术,2008,8(4):121-124. [4] Hoppe H C.Second-mover advantages in the strategic adoption of new technology under uncertainty [J].International Journal of Industrial Organization, 2000,18(2):315-338. [5] 黄学军,吴冲锋.不确定环境下研发投资决策的期权博弈模型[J].中国管理科学,2006,14(5): 33-37. [6] 王皓.反射倒向随机微分方程解及其在混合零和微分对策可逆投资问题及偏微分方程中的应用[D].济南:山东大学,2009. [7] Capisani L M,Ferrara A, Maqnani L.Design and experimental validation of a second-order sliding-mode motion controller for robot manipulators [J].International Journal of Control, 2009, 82(2): 365-377. [8] Nikoobin A, Haqhiqhi R.Lyapunov-based nonlinear disturbance observer for serialn-Link robot manipulators [J].Journal of Intelligent and Robotic Systems: Theory and Applications, 2009, 55(2/3): 135-153. [9] 张会娟, 张强.不确定性下非合作博弈强Nash均衡的存在性[J].控制与决策,2010,25(8):1251-1254. [10] 吴诗辉,杨建军, 郭乃林.三角模糊矩阵博弈的最优策略研究[J].系统工程与电子技术,2009,31(5):1231-1234. [11] 岳立柱,闫艳,仲维清.基于结构元方法的模糊矩阵博弈求解[J].系统工程理论与实践,2010,30(2):272-276. [12] 王才士,黄志远.量子随机 Cable 方程的白噪声分析方法[J].数学学报,2002,45(5): 851-862. [13] 肖兆银,周德云.遗传算法的泛函极值求解与应用[J].火力与指挥控制,2007,32(12):52-54. [14] 吴迪光.变分法[M].北京:高等教育出版社,1987. [15] 方志耕,刘思峰,陆芳,等.区间灰数表征与算法改进及其GM(1,1)模型应用研究[J].中国工程科学, 2005,7(2):57-61.3 泛函博弈模型
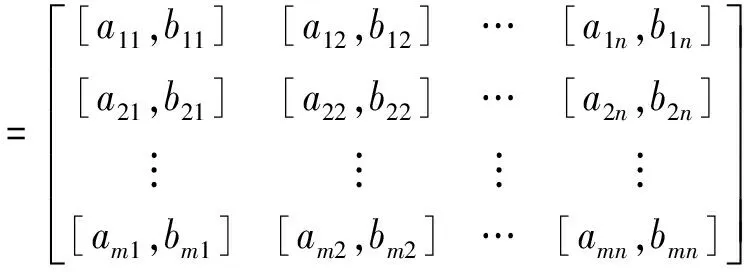
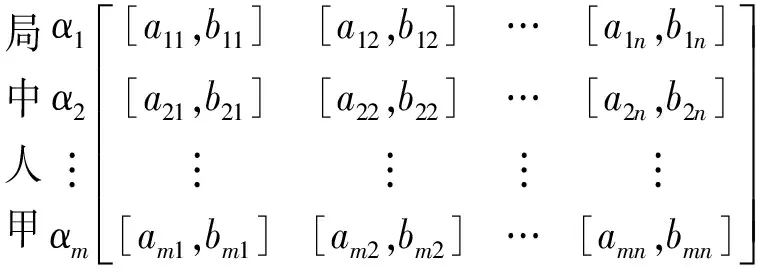
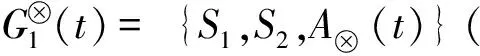
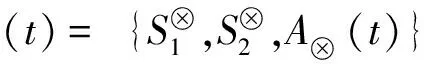
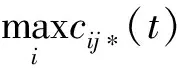
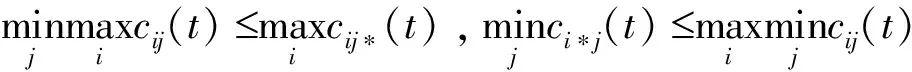
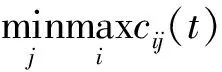
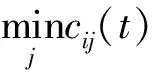
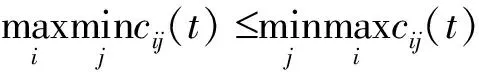
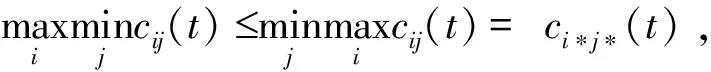
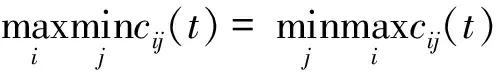
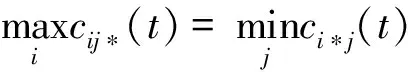
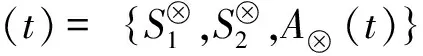
4 案例研究——盗版与打击盗版
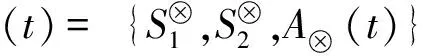

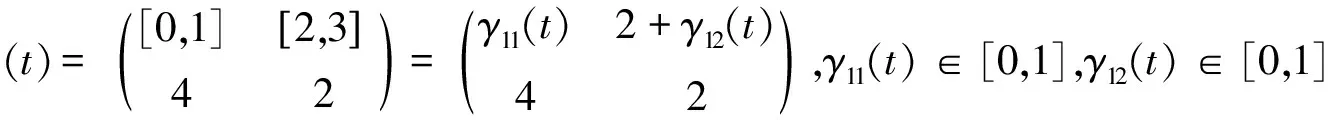
4.1 泛函博弈问题的最优解
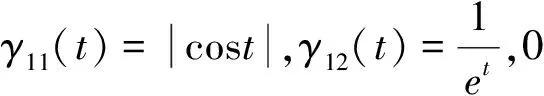
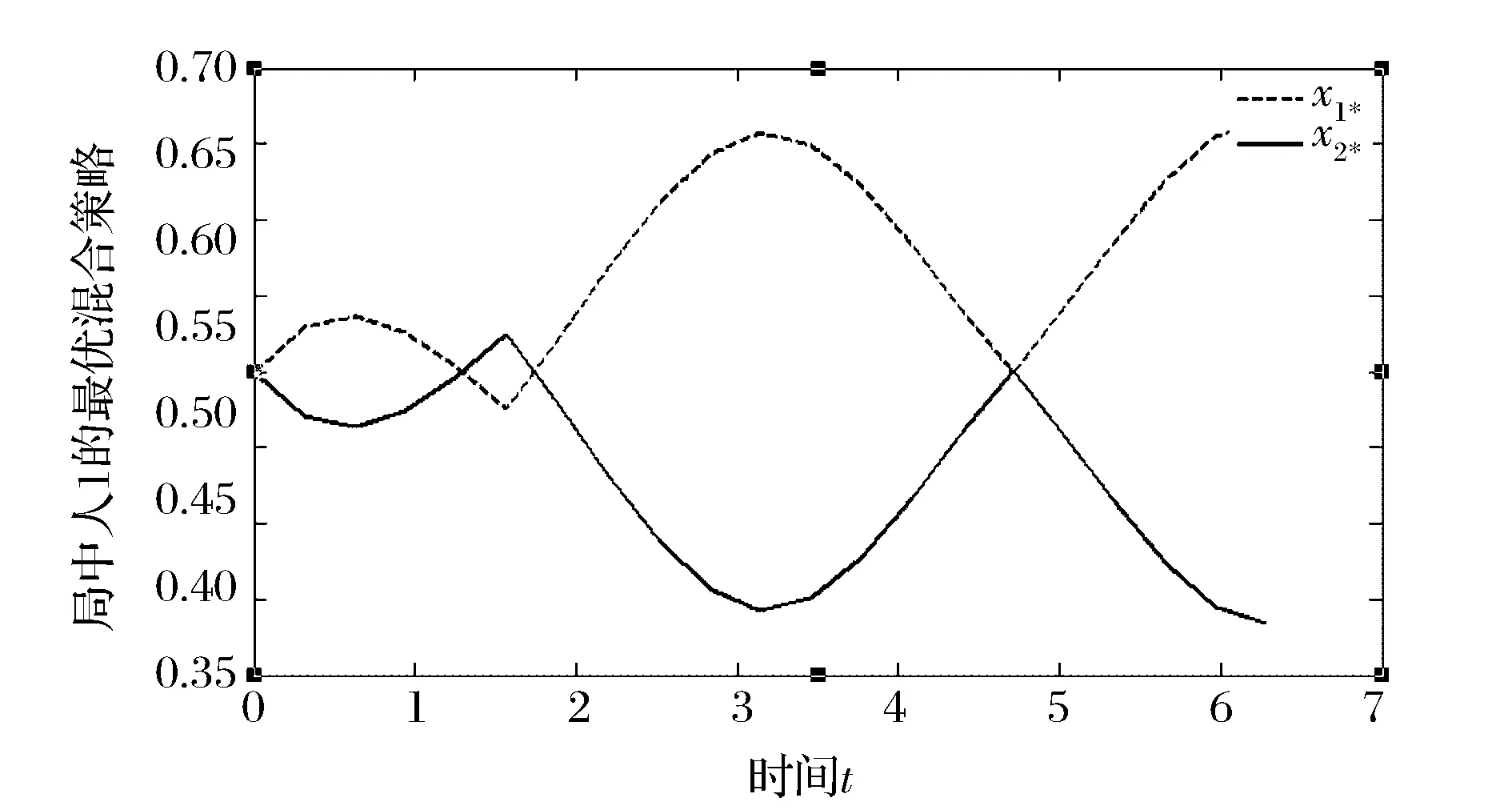
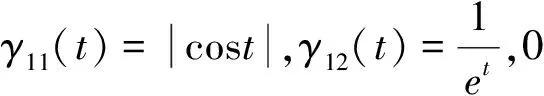
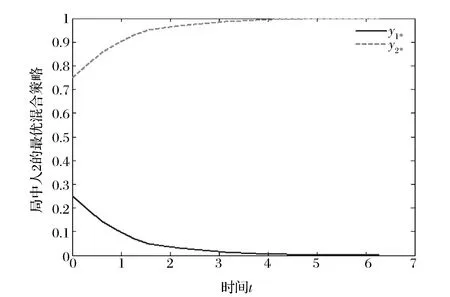
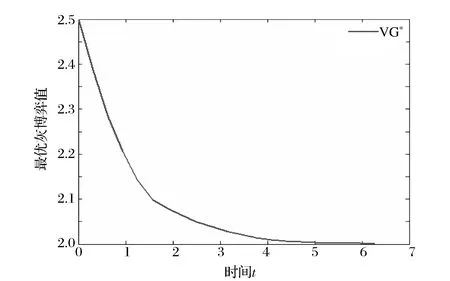
4.2 泛函区间灰数与标准区间数区别和差异

5 结语

