无漂移算术布朗运动下股指期货套期保值连续出清策略

唐衍伟，陈 刚，刘喜华

(青岛大学经济学院，山东 青岛 266071)

1 引言

在出清资产时，交易员不仅要考虑收益和风险，还要面对市场和自身的不确定性。股指期货套期保值涉及股票市场和股指期货市场，一般情况下，这两种资产是高度正相关的，而通过套期保值的反向操作则构造了两种高度负相关资产。对于已进行套期保值的股票现货，在出清股票头寸时，为了避免现货头寸风险暴露过大，应该保持现货与期货出清量以套期保值比例同步，从而确保持有头寸可以时时通过期货套期保值达到规避市场总体风险的目的。期货采用保证金交易制度，在进行期货出清时，衡量的是最终实现的出清成本，而不需要考虑其杠杆效应，而且股指期货可以认为是股票指数的近似替代，因此，可以将股票与股指期货同步出清问题纳入投资组合的框架下进行研究。

国外出清策略研究主要有：Lawrence和Robinson[1]利用均值-方差理论，通过融合市场风险的最优资产出清策略；Jarrow和Subramanian[2]引入流动性折扣因子和交易执行滞后时间函数，假定变现时间和出清量是外生给定的，通过最大化资产出清收益来决定持有期限，推导出最优资产出清策略；Bertsimas和Lo[3]采用随机动态规划法推导了最大化出清收益条件下的买入大部位投资组合的动态交易策略，证明了在市场冲击和交易量存在线性关系、资产价格过程是随机游走过程时，以一个常速率出售资产是最优选择；Almgren和Chriss[4-5]假定市场冲击分为瞬时冲击和永久冲击且都是线性的，通过均值-方差理论，提出了推导资产最优出清策略的框架，并提出融合流动性风险的VaR方法，研究表明最优执行策略是时间的双曲正弦和双曲余弦的线性组合形式；Huberman和Stanzl[6]在投资者的效用函数中引入执行成本的方差，利用随机动态规划方法实现最优策略的求解；Berkowitz[7]从需求弹性入手，用向下倾斜的需求曲线表示变现活动对市场价格的冲击，假定变现时间是外生变量，得到最优策略；Almgren[8]在冲击函数为多项式时，讨论了变现时间为可变时的最优变现策略；Dubil[9-10]延伸了Almgren和Chris[4]提出的模型来确定最终的出清期，假定交易以恒定速率进行，市场冲击函数为广义幂指数和与价格线性相关两种形式；Mö[11]在考虑日内市场流动性特性，采用指数价格冲击函数，建立了投资者指令重建的大部位投资组合的最优资产出清策略；Subramanian[12]在投资者风险偏好和资产价格运动的广泛假设下，建立了大宗资产投资者出清问题的优化模型，并证明大宗资产投资者在具有较强效用函数时能得到最优出清策略。Kim和Boyd[13]考虑时间不均匀线性价格冲击与波动、流动性与波动周期情况下，建立持有头寸预期资产价值与收益方差最大化的连续出清问题，通过求解第二类Fredholm积分方程或TPBVP问题求得出清轨迹。

国内研究主要有：林辉[14]在收益率为正态分布，相对价差和中间价格相互独立的前提下，研究了La-VaR模型，并将确定性等价效用和风险偏好引入多期La-VaR模型，采用匀速率出清逼近的方法，得到最优出清策略和La-VaR；胡小平[15]假定价格冲击函数为线性和随机，资产价格服从几何布朗运动，考虑离散和连续出清的情况，运用动态规划方法得到最优出清策略。储小俊等[16]对价格冲击模型作了一般性拓展，在交易对价格的影响为更接近于市场一般情况的随机、非线性价格冲击，建立了随机非线性价格冲击模型；以投资者的头寸变化作为交易策略的反映，结果表明在随机条件下考虑非线性价格冲击时，投资者的变现速度明显地受到限制，在变现期的绝大部分时间内以恒定速度变现，同时对最优策略进行了参数的敏感性分析：价格波动系数、风险厌恶系数越大，则前期变现速度越大、资产头寸减少越快；价格冲击系数、及瞬时价格冲击波动率的增加，变现头寸的减少越接近于直线的形式；刘宣会等[17]将随机LQ控制模型推广到系统状态为跳跃-扩散过程的随机LQ模型,采用随机Lagrange方法得到最优反馈控制,然后运用该框架去处理数理金融中的套期保值问题,最后得到了最优套期保值策略；唐衍伟等[18]假定股票和期货服从有漂移项的算术布朗运动，投资者效用为均值-方差形式，价格冲击为线性，在离散时间框架下，求解单只股票与股指期货套期保值同步出清问题，得到出清轨迹。

本文在Almgren和Chriss[4-5]研究框架下纳入期货套期保值，保持出清期间内套期保值比不变，假定资产价格服从无漂移项的算术布朗运动、永久和暂时价格冲击均为线性的情况下，研究单只股票与股指期货同步连续出清问题。

2 套期保值变现问题

考虑一名投资者在初始零时刻持有一种证券的头寸为X，计划在T时间内连续卖出全部股票，投资者在持有期第T个交易日结束时持有股票头寸为0。

定义在t时刻，t∈[0,T]，投资者持有的头寸为x(t)，证券的价格为St，则有：

x(0)=X,x(T)=0

(1)

变现速度为：

(2)

假设市场价格运动缺乏趋势性，认为市场价格服从如下无漂移项的几何布朗运动：

dS=SσdW(t)

(3)

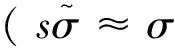
dS=σdW(t)

(4)

投资者变现交易引起的对市场不利影响分为永久冲击与瞬时冲击。所谓的永久冲击是指投资者的变现交易 (卖) 对市场价格的不利影响一直持续整个变现期[0,T]，而瞬时冲击只是在时间(t-dt,t)使内投资者的实际成交价格偏离市场的均衡价格。永久冲击响应和瞬时冲击响应都是变现速度的函数，考虑线性冲击响应：

(5)

由Almgren和 Chriss[5]知，由于永久冲击响应的存在，市场价格运动中漂移项变为-g(v(t))，市场价格变为：

(6)

由于瞬时冲击响应h(v(t))的存在，投资者真正实现的交易价格为：

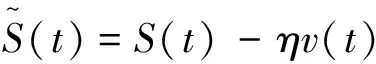
(7)

投资者的执行成本为：

(8)

其中：

(9)

将(9)代入(8)：

(10)

因为：

(11)

(12)

EC的数学期望为：

(13)

EC的方差为：

(14)

同理，假定股指期货价格服从如下算术布朗运动：

dSf=σfdW(t)

(15)

市场的永久冲击系数和暂时冲击系数分别为γf>0、ηf>0，套期保值的交易方向同股票交易方向相反，若股票为卖出变现，则期货为买入变现。

为了保持股票和期货的同步，股票和期货头寸应按套期保值比φ进行同步变现：

(16)

期货执行成本为：

(17)

股指期货套期保值股票和期货同步执行成本为：

(18)

因此，执行成本的期望和方差可分别求得为：

(19)

式中，ρ为股票和期货价格的相关系数，由于股票和期货的操作方向相反，因此在计算方差时ρ取负号，φ为套期保值比。

令

(20)

上式可写为：

(21)

3 变现策略求解

投资者选择策略(x(t),v(t))，使得下式取最小值：

U=E(EC)+λV(EC)

(22)

λ是资者的风险偏好，λ<0时，投资者偏好风险；当λ=0时投资者风险中性；当λ>0时，投资者风险厌恶。以下仅讨论风险厌恶的理性投资者。

令:

(23)

则x*(t)最小值使得U取得最小值，等价于x*(t)使得指标泛函J(x(t))取得最小值。

令:

(24)

为使J(x(t))取得最小值，F(x(t))应满足如下形式的欧拉方程：

(25)

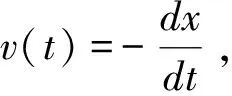
(26)

将式(24)代入上式并化简得到：

(27)

当λ>0时，利用边界条件x(0)=X，x(T)=0可得方程(27)的通解为：

(28)

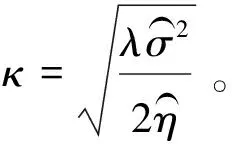
期货出清轨迹为xf(t)=φx(t)。

4 参数分析

投资者初始持有股票头寸为x(0)=X=107股，计划在T=5天内出清，股票的方差为σs=0.045，永久冲击系数为：γs=4.5×10-7，暂时冲击系数为：ηs=1.50×10-7，股指期货的方差为σf=0.025，永久冲击系数为：γf=2.5×10-8，暂时冲击系数为：ηf=5.5×10-8，套期保值比为φ=0.5，股票和期货相关系数为ρ=0.8，假定投资者的风险厌恶系数为λ=10-4，参数计算结果如下表：

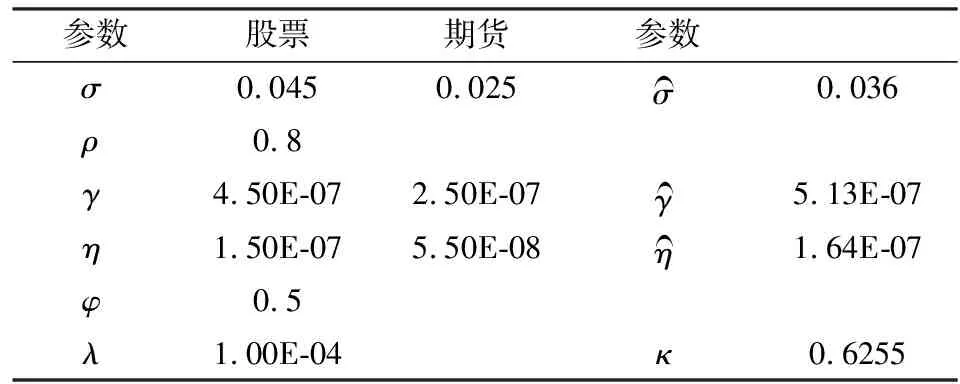
表1 出清参数计算

(一)风险厌恶系数对出清轨迹的影响

当风险厌恶程度较大时，投资者倾向于在出清初期出清较大规模的头寸，以降低后期的风险，而当风险厌恶程度较小时，投资者倾向于更小的出清头寸，也更接近匀速率出清，如图1所示。

图1 不同风险厌恶程度的出清轨迹

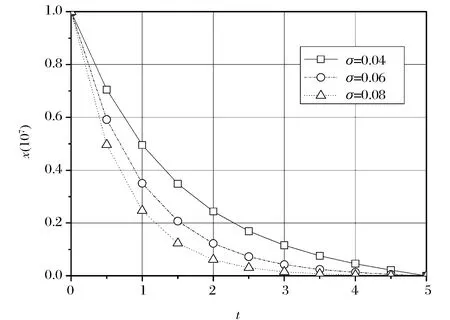
图2 不同组合标准差的出清轨迹

(二)组合标准差对出清轨迹的影响

组合标准差越大，则出清轨迹下移，投资者在出清初期更倾向于出清更多的头寸以降低波动风险；当组合标准差变小，出清轨迹上移，投资者更倾向于更缓慢出清，如图2所示。

(三)相关系数不变，不同套期保值比的出清轨迹

(1)ρ=0时或φ=0时，出清过程退化为不考虑期货套保的情况，即纯粹的股票出清；

(2)当ρ>0且φ>0，随套期保值比的增加，出清轨迹向上移动，即随套期保值比的增加，每次的出清量逐渐减少，投资者更倾向于缓慢的出清过程，如图3所示。

(3)当ρ<0且φ>0，随套期保值比的增加，出清轨迹向下移动，即随套期保值比的增加，每次的出清量逐渐增加，投资者倾向于更快速的出清过程，如图4所示。

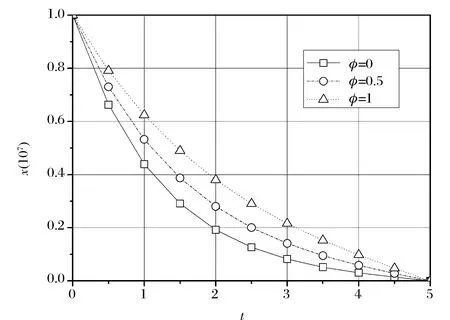
图3 ρ=0.8时不同套期保值比的出清轨迹

图4 ρ=-0.8时不同套期保值比的出清轨迹

(四)套期保值比不变，不同相关系数的出清轨迹(图5)

(1)当φ>0且ρ>0，随相关系数的增加，出清轨迹向上移动，即随相关系数的增加，每次的出清量逐渐减少，出清量与相关系数呈反向变化，且随套期保值比的增加，其差异越大。

(2)ρ<0时，φ>0，随相关系数的增加，出清轨迹向下移动，即随相关系数绝对值的增加，每次的出清量逐渐减增加，出清量与相关系数绝对值呈同向变化，且随套期保值比的增加，其差异越大。

图5 不同相关系数的出清轨迹

5 结语

假定股票和期货服从无漂移项的算术布朗运动，投资者效用为均值-方差形式，价格冲击为线性冲击，在连续时间框架下，求取了单只股票与股指期货套期保值在给定出清时间内的同步出清问题，得到出清轨迹。

参数分析表明：当风险厌恶程度较大时，投资者倾向于在出清初期出清较大规模的头寸，以降低后期的风险；组合标准差越大，则出清轨迹下移，投资者在出清初期更倾向于出清更多的头寸以降低波动风险；当ρ>0，随套期保值比的增加，投资者更倾向于缓慢的出清过程，当ρ<0则相反；在给定套期保值比的情况下，出清速率与相关系数呈反向变化。

由于采用股指期货进行套期保值，使得组合标准差降低，起到平抑组合波动的作用，因而可以采取比无套期保值情况下更为缓慢的出清过程。

参考文献：

[1] Lawrence C，Robinson G.Liquidity, dynamic hedging and value at risk[J].Risk Management for Financial Institutions, 1997，1(9)：63-72.

[2] Jarrow R, Subramanisan A.Mopping up liquidity[J].Risk, 1997, 10: 170-173.

[3] Bertsimas D，Lo A W.Optimal control of execution costs[J].Journal of Financial Markets, 1998, 1(1): 1-50.

[4] Almgren R, Chriss N.Value under liquidation[J].Risk, 1999, 12(12): 61-63.

[5] Almgren R, Chriss N, Optimal execution of portfolio transactions[J], Journal of Risk, 2000,3: 5-39.

[6] Huberman G, Stanzl W.Optimal liquidity trading[R].Working paper, Columbia University, 2001.

[7] Berkowitz J.Incorporating liquidity risk into VaR models[R].Working Paper, 2000.

[8] Almgren R.Optimal execution with nonlinear impact functions and trading-enhanced risk[R].Working paper, 2001.

[9] Dubil R.The modeling of liquidity in the valuE-at-risk framework[D].Connecticut: University of Connecticut 2001.

[10] Dubil R.Optimal liquidation of large security holding in thin market[M].Journal of Financial Economics, 2002.

[11] Mö B.Strategic trading in illiquid markets[M].Berlin Heidelberg: Springer-Verlag , 2005.

[12] Subramanian A.Optimal liquidation by a large investors[J].SIAM Journal on Applied Mathematics, 2007.

[13] Kim S J, Boyd S.Optimal execution under time-inhomogeneous price impact and volatility[J].Preprint, 2008.

[14] 林辉.金融市场微观结构视角的La-VaR模型[D].南京：东南大学，2004.

[15] 胡小平.La-ES与最优变现策略模型研究[D].上海：上海交通大学，2006.

[16] 储小俊.在随机非线性价格冲击下的最优变现策略研究[J].中国管理科学，2007，15(5): 137-142.

[17] 刘宣会.于随机Lagrange方法的最优套期保值策略[J].系统工程理论实践, 2010, 30(6): 1034-1039.

[18] 唐衍伟.算术布朗运动下股指期货套期保值离散出清策略[J].系统工程理论实践, 2012.