具有不同类型信息的风险投资商与投资企业多指标双边匹配决策方法
万树平,李登峰
(1.江西财经大学信息管理学院,江西 南昌 330013;2.福州大学管理学院,福建 福州 350108)
1 引言
风险投资是风险投资公司将自己的资金、品牌、网络、管理等资源与风险企业的技术、人力资源有机结合,实现风险企业高速成长,并从中获得高额利润的过程。投资企业的发展需要风险投资商的资金支持,风险投资商也希望找到合适的投资企业进行投资[1]。风险投资商与投资企业的合理匹配能够尽量使双方都达到满意的结果, 有利于提高风险投资活动的成功率,降低风险,实现双赢。风险投资商与投资企业的匹配是一个双向选择过程,为做出正确的投资决策,风险投资商对投资企业的技术、市场潜力和规模以及管理队伍等方面进行仔细的审查与评估;寻求风险投资的投资企业在筛选投资公司时,往往需要考虑多个因素,比如:企业所需投资的规模、地理位置、发展阶段和发展状况、销售额及盈利状况、经营范围等。因此,风险投资商与投资企业的匹配可归结为一类多指标双边匹配问题。
匹配研究起源于男女婚姻匹配与大学录取问题[2],随后,双边匹配问题研究引起了学者们的重视,如电子商务环境下供需双边匹配[3-4]、人力资源管理中员工与岗位双边匹配[5-6]、IT服务供需双边匹配[7]和电子中介的交易匹配[8]等。Sφrensen[9]基于双边匹配模型构建了风险投资的结构模型,用以解释得到拥有更多经验的风险投资商投资的公司,更有可能公开上市。陈希等[1]构建了风险投资商与投资企业双方互评的匹配评价指标体系,提出了基于公理设计的匹配决策方法。该方法能有效地衡量风险投资商与投资企业的匹配程度,但仅考虑了指标评价值信息为区间数和语言变量的情形。在现实的风险投资商与投资企业匹配问题中,由于涉及多个不同的定性和定量评价指标,评价信息经常是以多种形式给出的。对定量指标,可能以实数、区间数或三角模糊数给出,例如,投资企业对风险投资商的回报率进行评价时,会给出一个大致范围[8%,12%],对投资成功率评价时表示为三角模糊数(0.5,0.65,0.7),即最可能是0.65,最低是0.5,最高是0.7;对定性指标,可能以语言变量或直觉模糊数给出,例如,风险投资商对投资企业的企业家素质进行评价时,往往会采用“高”、“较高”等语言变量来表示,对投资环境和税收优惠进行评价时可能会给出以0.5的隶属度满意,以0.3的非隶属度不满意,还存在0.2的不确定是否满意这三方面的信息,即采用直觉模糊数<0.5,0.3>表示。
现有的双边匹配方法大多是建立在期望效用理论基础之上的,即假设决策者是完全理性的。然而,在实际的决策过程中,决策者在行为上并不总是追求效用最大化,而是往往会根据某些参考点来衡量决策的收益和损失风险。可能会因参考点的选择不同,使得每次决策都随之改变,即表现为参照依赖。在参考点上,人们更重视预期与结果的差距而不是结果本身。决策者对待损失的感知比等量的收益更加敏感,即表现为损失规避[10-11]。这样,运用期望效用理论,有时就不能准确地描述决策者在实际决策过程中表现出的参照依赖和损失规避这种心理行为特征[12],而已有的双边匹配方法难以处理考虑决策者有限理性特征与复杂心理行为的情况。为此,本文考虑决策者的心理行为,利用前景理论[10-12]和TODIM (an acronym in Portuguese of Interactive and Multicriteria Decision Making)[13-14]方法研究具有不同类型信息的风险投资商和投资企业的多指标双边匹配问题。
2 具有不同类型信息的风险投资商与投资企业双边匹配问题
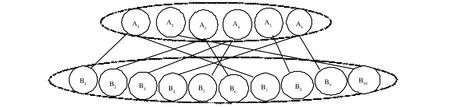
在风险投资商与投资企业的匹配过程中,存在着三方决策主体:风险投资商、投资企业和投资中介。风险投资商将其对投资企业的期望水平信息提供给中介,中介客观地给出对投资企业的实际评价信息。投资企业将其对风险投资商的期望水平信息提供给中介, 中介客观地给出对风险投资商的实际评价信息。中介根据双方的期望水平信息和实际评价信息, 以使双方都达到满意为目标, 聚合风险投资商和投资企业并形成合理的匹配对。图1为具有不同类型信息的双边匹配示意图。
所有风险投资商记做集合A={A1,A2,…,Am},其中Ai为第i个风险投资商。风险投资商对投资企业的所有评价指标(属性)记做集合C={c1,c2,…,cf},其中ch为第h个评价指标;对应于C的指标权重向量为w=(w1,w2,…,wf),其中wh为指标ch的权重,满足归一性要求:0wh1,。所有投资企业记做集合B={B1,B2,…,Bn},其中Bj为第j个风险企业。投资企业对风险投资商的所有评价指标记做集合Y={y1,y2,…,yg},其中yk为第k个评价指标;对应于Y的指标权重向量为ω=(ω1,ω2,…,ωg),其中ωk为指标yk的权重,满足归一性要求:0vk1,。
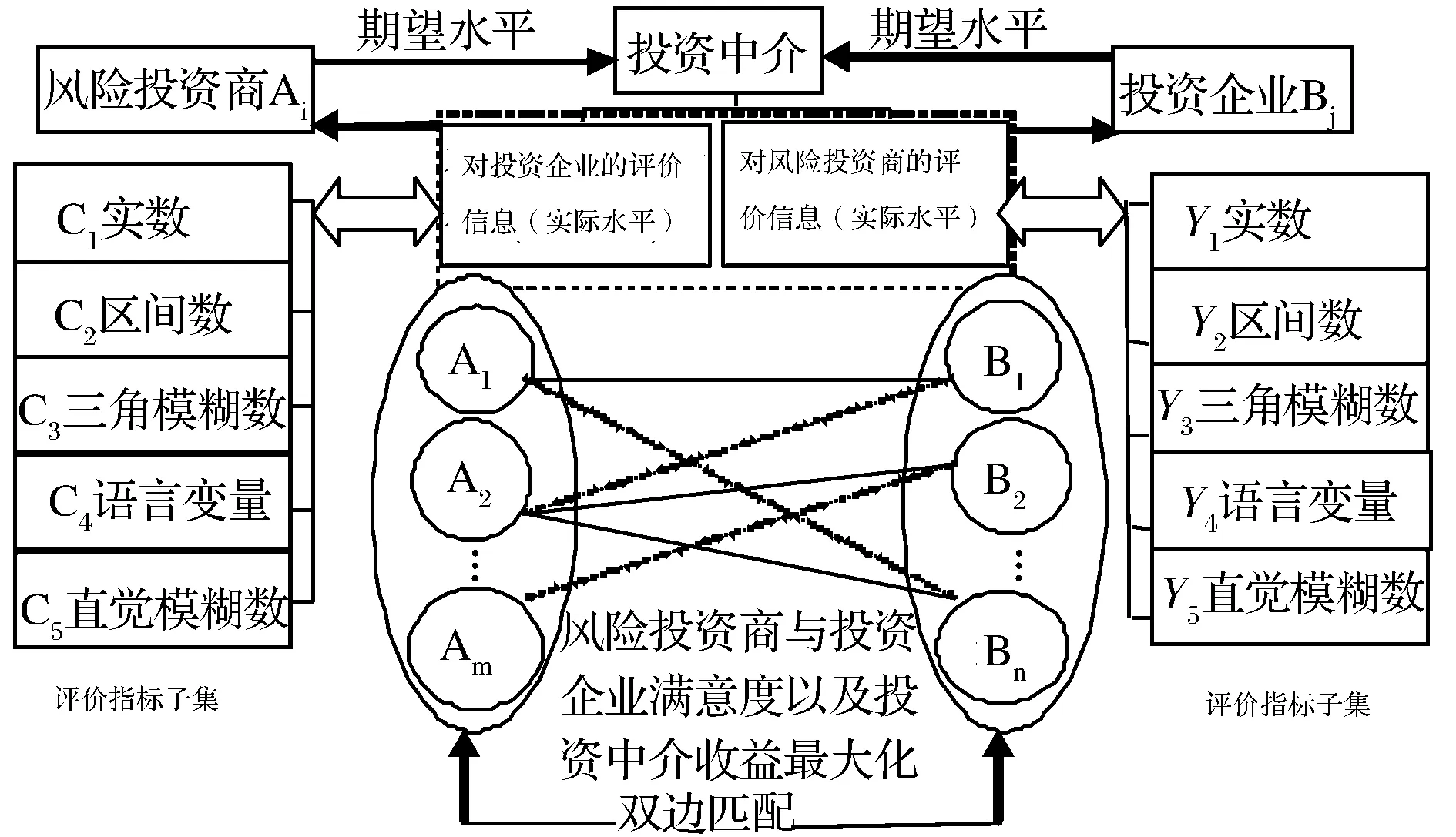
图1 具有不同类型信息的风险投资商与投资企业双边匹配示意图
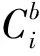
设风险投资商Ai对指标ch的期望水平为:
(1)
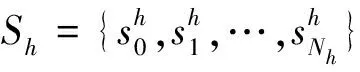
投资中介对投资企业Bj进行评价,给出其在指标ch的实际水平为:
(2)
设投资企业Bj对指标yk的期望水平分别为
(3)
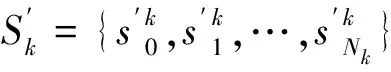
投资中介对风险投资商Ai进行评价,给出其在指标yk的实际水平为
(4)
风险投资商Ai至多可投资的投资企业数为θi个,一个投资企业至多可与一个风险投资商匹配。本文考虑的是依据上述期望水平和实际水平信息,通过使用某种决策方法,将风险投资商与投资企业匹配,使得双方的满意度尽可能达到最大,同时投资中介的收益也最大化。
3 具有不同类型信息的风险投资商与投资企业双边匹配决策模型及方法
为消除不同物理量纲对决策结果的影响,首先需将各指标的评价值信息进行规范化处理。类似于Li Dengfeng[15]的处理,以eih为例说明规范化方法。
实数eih=dih(ch∈C1)规范化为:
(5)
其中,dmaxh=max{dih|i=1,2,…,m}。
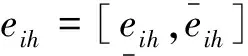
(6)
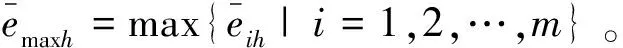
三角模糊数eih=(aih,bih,cih)(ch∈C3)规范化为:
(7)
其中,cmaxh=max{cih|i=1,2,…,m}。
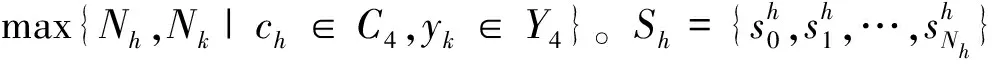
(8)
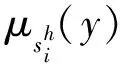
语言变量eih=sih∈Sh可由式(8)转化为模糊集φ(sih),采用向量表示为φ(sih)=(μih0,μih1,…,μihL)(ch∈C4),简记为lih=(μih0,μih1,…,μihL)。
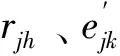
针对指标评价值信息具有不同类型,给出规范化后的指标值期望水平和实际水平之间的距离。定义rjh与eih的距离d(rjh,eih)为:
(1)若rjh与eih都为实数,则d(rjh,eih)=d(gjh,dih)=|gjh-dih|;
(2)若rjh与eih都为区间数,则:
其中,p>0为距离参数;
(3) 若rjh与eih都为三角模糊数,则
(4)若rjh与eih都为语言变量,则:
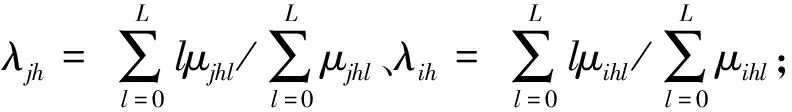
(5)若rjh与eih都为直觉模糊数,则:
其中,γjh=1-tjh-fjh、πih=1-μih-υih为犹豫度。
然后针对决策者参照依赖的心理行为特征,即决策者把结果看作相对于参照点的收益或损失[10],风险投资商Ai以对指标ch的期望水平eih作为参照点,将投资企业Bj关于指标ch的实际水平rjh与之比较,根据前景理论[10],可定义实际水平rjh相对于期望水平eih的益损值为:
(9)
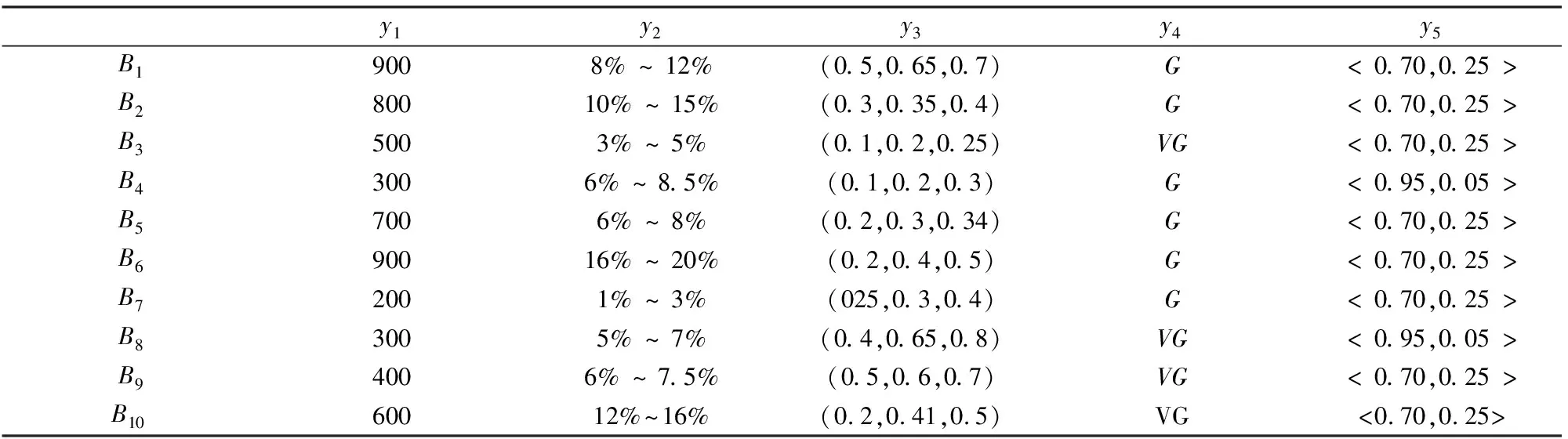
其中,d(rjh,eih)为rjh与eih的距离,rjh≥eih表示rjh不小于eih,此时Δ(rjh,eih)为收益;rjh 考虑决策者损失规避的心理行为特征, 即决策者对待损失的感知比等量的收益更加敏感[11], 依据TODIM方法[ 13-14]的基本思想, 计算决策者对每个方案在各属性下的益损值的感知价值。为了将各属性下的益损值的感知价值转化到同一维度上[14], 需要计算每个属性相对于参照属性的相对权重, 例如,对属性ch,其相对于参照属性的相对权重为: (10) 其中,w*=max{wh|h=1,2,…,f},对应于w*的属性c*被视为参照属性,c*∈C。 进而计算风险投资商Ai对益损值Δ(rjh,eih)的感知价值为: (11) 由式(11)可计算风险投资商Ai对投资企业Bj的总体感知价值为: (12) Ai对Bj的总体感知价值是Ai所能感知到的收益和损失进行权衡后对Ai期望水平与Bj实际水平吻合程度的总体评价,V(Ai,Bj)的值越大,则Ai对其期望水平与Bj的实际水平吻合程度越满意,因而两者的匹配度越高。 (13) 由式(13)可计算投资企业Bj对风险投资商Ai的总体感知价值为: (14) V(Bj,Ai)的值越大,则Bj对其期望水平与Ai的实际水平吻合程度越满意,两者匹配的程度越高。 设矩阵X=(xij)m×n,其中,xij=1表示风险投资商Ai与投资企业Bj匹配;xij=0表示风险投资商Ai与投资企业Bj不匹配,构建如下多目标优化模型: max{Z1(X),Z2(X),Z3(X)} 一是城区生态水系规划绘就。根据市委、市政府建设卓越秀美“江北水城·运河古都·生态聊城”的重大战略决策,聊城先后编制完成了《聊城市现代水网建设规划》《聊城市生态文明城市实施方案》《聊城市城区环城水系规划》,明确提出了依托南水北调东线干线,引黄引金(金堤河)和引卫(卫河、卫运河)工程,实施平原水库、河道拦蓄等工程,充分利用拦蓄雨洪水,连通“四横、五纵”,初步形成跨流域调水大动脉、防洪调度大通道和水系生态大格局。 (15a) (16) max {μ} (17a) 极大极小方法确定的模糊最优解或满意解X*可保证最差的目标函数的优属度达到最大,是一种保守的处理方法,适合于保守型决策者采用。模型(17)中目标函数和约束条件均是线性的,可采用整数规划方法进行求解。 根据上面的讨论,可将考虑多种形式信息的双边匹配决策方法的具体步骤归纳如下: Step 1 识别风险投资商与投资企业的评价指标; Step2 抽取风险投资商与投资企业的各个评价指标信息(或评价值); Step3利用式(5)-(8)将各个指标评价值规范化; Step4 根据式(9)-(12)计算风险投资商Ai对投资企业Bj的总体感知价值(i=1,2,…,m;j=1,2,…,n); Step5根据式(13)-(14)计算投资企业Bj对风险投资商Ai的总体感知价值(i=1,2,…,m;j=1,2,…,n); Step6 求解模型(17)得到最优匹配结果。 风险投资匹配的三方决策主体是:6个风险投资商(即:今日资本A1,联想投资有限公司A2,摩根士丹利A3,美国华平投资集团A4,天使投资人A5,大学捐赠基金A6)、10个投资企业(即:甲骨文B1,思科B2,双汇集团B3, 半导体芯片公司B4,南孚电池B5,腾讯B6,哈药集团B7,蒙牛B8,阿里巴巴B9,软件企业B10)和某风险投资中介。 风险投资商选取8项指标(即:投资回收期c1(单位为年),年投资报酬率c2,期望风险c3,技术水平c4,市场的可进入性c5,企业家素质c6,投资环境c7,税收优惠c8)对投资企业进行评价,根据以往经验和市场调查以及统计分析,给出8项指标的期望水平,如表1所列,其中,c1与c2为定量指标,由于市场环境的不确定性和客观事物的复杂性,c2只能给出大致的范围,即采用区间数表示;c3采用百分比、c4采用10分制给出最可能性值和上、下限,即采用三角模糊数表示;指标c5和c6的评价值分别取自语言短语集S5={弱/低W,中等/一般M,强/高S}和S6={非常差/非常低VL,较差/较低L,中等/一般M,较好/较高VG,非常好/非常高VG};指标c7, c8采用直觉模糊数表示。投资中介聘请律师和会计师等专业人员对10个投资企业进行评价,给出投资企业在指标{c1,c2,…,c8}下的实际水平,如表2所列,指标权重向量由专家给定为w=(0.15, 0.25, 0.20, 0.15, 0.06, 0.12, 0.08, 0.09)T。 投资企业选取5项指标(即:投资额度y1(单位为万元),投资回报率y2,投资成功率y3,信誉y4,企业家素质y5)对风险投资商进行评价,分别采用实数、区间数、三角模糊数、语言变量和直觉模糊数表示,给出5项指标的期望水平,如表3所列,其中,指标y4的评价值取自语言短语集S6。投资中介聘请风险投资机构领域的资深专家对风险投资商进行评价,给出风险投资商在指标{y1,y2,…,y5}下的实际水平,如表4所列,专家给出的指标权重向量为ω=(0.20, 0.35, 0.22, 0.13, 0.10)T。每个风险投资商最多可投资的投资企业数θi为2(i=1, 2,…, 6)。 投资中介需要根据收到的信息,考虑尽量满足风险投资商和投资企业的意向和要求,使两者在各自评价指标下的期望水平和实际水平的吻合程度最高,即保证风险投资商和投资企业的匹配程度最高,同时投资中介的收益最大。 表1 风险投资商对投资企业的期望水平 表3 投资企业对风险投资商的期望水平 表4 风险投资商的实际水平 图2 匹配结果 与陈希等[1]相比,本文方法优点主要体现在: (1) 考虑了指标评价值为不同类型信息,且相对于不同的指标,语言变量取值于不同粒度的语言标记集,而陈希等[1]仅考虑了区间数和语言变量(不同指标的语言评价值取值于同一语言标记集)的情形,所以无法处理类似于上述具有不同类型信息的匹配决策问题。 (2) 构建的匹配模型不仅考虑了风险投资商、投资企业的总体感知价值尽能达到最大,而且考虑了投资中介的收益最大化,模型更加吻合实际,而陈希等[1]没有考虑投资中介的收益。 (3) 利用总体感知价值度量风险投资商、投资企业的匹配度,充分考虑了决策者的参照依赖和损失规避的心理行为,而陈希等[1]未考虑决策者有限理性特征与复杂心理行为的情况。 本文根据现实风险投资商与投资企业多指标双边匹配问题的特点,提出了具有不同类型信息的匹配决策方法。该方法针对决策者参照依赖和损失规避的心理行为特征, 基于前景理论和TODIM方法计算投资企业和风险投资商的总体感知价值。所构建的匹配模型考虑了投资中介的收益,更加吻合实际,给出的匹配方法概念清晰,计算简单,具有较强的实用性。本文中对于各指标考虑的是期望水平与实际水平信息形式相同的情形,但在现实问题中,某指标的期望值与实际值也可能采用不同信息形式描述,此时,只需要将不同类型的期望水平与实际水平信息转化为相同类型的形式[1,15,20],则仍可采用本文定义的期望水平与实际水平的距离公式,因而所提出的匹配方法仍然适用。例如,期望水平是区间数[a,b],实际水平是实数c,则可将实数c转化为区间数[c,c]。 参考文献: [1] 陈希, 樊治平.基于公理设计的风险投资商与风险企业双边匹配[J].系统工程, 2010, 28(6): 70-75. [2] Gale D, Shapley L.College admissions and the stability of marriage [J].American Mathematical Monthly, 1962, 69(1): 9-15. [3] Janssen M, Verbraeck A.Comparing the strengths and weaknesses of Internet-based matching mechanisms for the transport market [J].Transportation Research Part E, 2008, 44(3): 475-490. [4] Sarne D, Kraus S.Managing parallel inquiries in agents’ two-sided search [J].Artificial Intelligence, 2008, 172 (4-5): 541-569. [5] Lin H T.A job placement intervention using fuzzy approach for two-way choice [J].Expert Systems with Applications, 2009, 36(2): 2543-2553. [6] Huang Denghui, Chiu H N, Yeh R H, et al.A fuzzy multi-criteria decision making approach for solving a bi-objective personnel assignment problem [J].Computers & Industrial Engineering, 2009, 56(1): 1-10. [7] 陈希, 樊治平, 李玉花.IT服务供需双边匹配的模糊多目标决策方法[J].管理学报, 2011, 8(7): 1097-1011. [8] 蒋忠中, 袁媛, 樊治平.电子中介中具有数量折扣的多属性商品交易匹配问题研究[J].中国管理科学, 2010, 18(6): 122-130. [10] Kahneman D, Tversky A.Prospect theory: An analysis of decision under risk [J].Econometrica, 1979, 47(2): 263-291. [11] Tversky A, Kahneman D.Advances in prospect theory: Cumulative representation of uncertainty[J].Journal of Risk and Uncertainty, 1992, 5(4): 297-323. [12] Schmidt U, Zank H.A simple model of cumulative prospect theory[J].Journal of Mathematical Economics, 2009, 45(3): 308-319. [13] Gomes L F A M, Lima M M P P.TODIM: Basic and application to multi-criteria ranking of projects with environmental impacts [J].Foundations of Computing and Decision Sciences, 1992, 16(4): 113-127. [14] Gomes L F A M, Rangel L A D.An application of the TODIM method to the multicriteria rental evaluation of residential properties[J].European Journal of Operational Research, 2009, 193(1): 204-211. [15] Li Dengfeng, Huang Zhigong, Chen Guohong.A systematic approach to heterogeneous multiattribute group decision making[J].Computers & Industrial Engineering, 2010, 59(4): 561-572. [16] 徐泽水, 达庆利.区间数排序的可能度法及其应用[J].系统工程学报, 2003, 18(1): 67-70. [17] 徐泽水.对方案有偏好的三角模糊数型多属性决策方法研究[J].系统工程与电子技术, 2002, 24(8): 9-13. [18] Hong D H, Choi C H.Multi-criteria fuzzy decision-making problems based on vague set theory[J].Fuzzy Sets and Systems , 2000, 114: 103-113. [19] Wan S P, Li D F.Fuzzy LINMAP approach to beterogeneous MADM considering the comparisons of alternatives with hesitation degress[J].Omega, 2013, 41(6):925-940. [20] 李登峰.模糊多目标多人决策与对策[M].北京:国防工业出版社, 2003.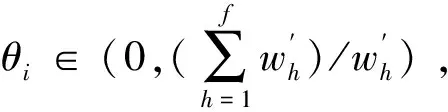
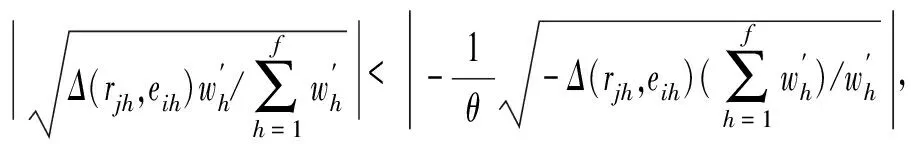
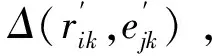
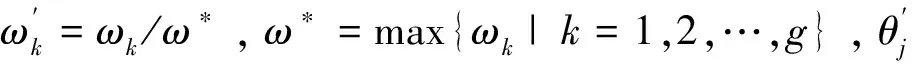
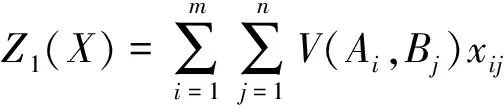
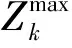
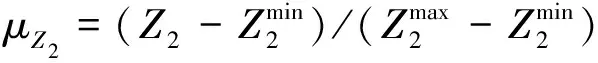
4 实例计算与分析


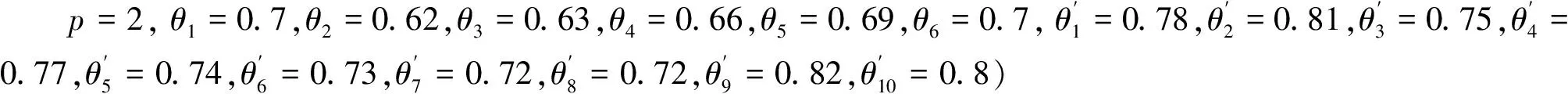
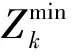
5 结语

