基于两阶段决策的封闭式基金价格控制问题研究

，

(1.西安理工大学经济管理学院,陕西 西安 710048；2.西安交通大学应用经济学博士后流动站，陕西 西安710061)

1 引言

虽然开放式基金占据了中国基金市场的大部分份额，但由于市场对于“封转开”形势的普遍看好，封闭式基金已成为诸多机构投资者建仓的重点品种。2005年4月31日，保险资金投资基金的规模达到890.29亿元，一举创出历史新高，而这次保险资金增资的主要对象为封闭式基金。由于LOF(上市型开放式基金)的推出为封闭式基金逐步转为开放式基金提供了有力的技术手段，在封闭式基金高折价的现状条件下，如果某一封闭式基金一旦“封转开”，巨大的套利机会将随之降临[1]。特别是在牛市的背景下，“封转开”将使基金持有人获得两大收益：一是基金净值的增加，二是“封转开”带来价格回归价值的套利。截止目前市场共有20多支封闭式基金已成功进行了“封转开”，仅2007年就有18支，目前还有28支封闭式基金未到期，而最终选择“封转开”也是这些基金到期之后的必然选择。

由于封闭式基金的交易在二级市场进行，它的价格在一定程度上由供求关系决定，然而在我国金融市场制度建设尚不完善的情况下，特别是在“封转开”巨大套利机会的驱使下，资金巨大的投资者一方面可能籍此大量进行封闭式基金建仓，另一方面也可能借助市场对于封闭式基金的热炒，进一步通过在二级市场对封闭式基金价格进行控制来获得巨额利润。然而，对于基金价格问题的研究已有文献多是从基金价格与资产净值之间的关系来进行分析，Flynn[2]讨论了噪声交易，套利与资产价格对于美国封闭式基金折价的影响。实证研究认为无法确定基金套利行为、管理费用对封闭式基金折价造成影响，但是噪声交易对于基金折价的有显著影响。Shane[3]讨论了信号传递、差异化策略与基金折价的关系，研究结果表明高质量的基金再结合差异化策略可很好的降低基金折价。张世英、王东[4]研究了投资基金的价格监管和风险控制问题，基于模糊随机理论，从基金净值角度定义了投资基金价格风险的测度。宋颂兴[5]基于折现法从基金净值和基金现值的视角分析了封闭式基金定价问题。肖国荣[6]认为基金价格变化规律相当复杂，影响因素间非线性程度相当的高，传统预测方法不能很好反映非线性规律，导致基金价格预测精度不高。赵秀娟等[7]运用CGARCH模型、Granger因果检验分析了深市基金指数(封闭式基金价格指数)与开放式基金、A股、B股、仿真股指期货以及债券市场的主要指数在波动上的关联性，同时分析了极端风险对条件波动的溢出效应。王良、冯涛[8]在高频数据条件下，研究了中国ETF基金价格"已实现"波动率与跟踪误差之间是否存在着因果关系并存在着信息的先导效应。

与以上研究思路不同，本文考虑了一种交易状况：在某一交易时间段内，二级市场上某支封闭式基金的交易者只有一个可对基金价格进行控制的基金投资者(例如保险公司、持有巨额资金的内幕交易者等，类似庄家)和无穷多单个散户基金投资者，在此我们称前一类型的基金投资者为“庄家”型基金投资者。“庄家”型基金投资者可控制封闭式基金的价格(如不特别说明，以下的基金全部指封闭式基金)。此外，该基金投资者期初持有的投入资金额度有限(在该交易时间段内全部投入)。为了更好地使得资金效用发挥到最大，在交易时间段的期初，“庄家”型基金投资者须考虑初始持有资金的额度限制，依据基金在各个时刻的期望收益率及其收益风险来求得对应时刻的最优投资值(其中正值表示投入，负值表示收回)，然后再来确定基金价格控制的最优策略。因此，本文认为“庄家”型基金投资者的决策可分为两个阶段：第一阶段基于各时刻的期望收益率及收益离差来确定该基金投资者在给定交易时段中各个时刻的最优投资值，第二阶段以第一阶段得到的各时刻的最优投资值为约束来确定基金价格的最优控制序列。

对于第一阶段可建立使“庄家”型基金投资者期望收益最大、收益平均绝对离差最小(风险最小)的双目标模型，变换为一个单目标模型后利用库恩-塔克条件进行求解；对于第二阶段则以第一阶段求得的各时刻最优投资值为约束，以“庄家”型基金投资者在该交易时间段内的现金支付为极小值(现金收益的极大值)来建立目标函数，而其为一个带约束的非线性规划问题。由于求解此类问题常采用惩罚函数法来将带约束的非线性规划问题转化为无约束问题，但是随着惩罚因子趋于无穷大或零，目标函数值随着迭代点向最优点靠近而逐渐变坏，使一般无约束优化方法失效。因此本文采用了一种改进的遗传算法，利用该方法不但能够收敛到最优解的邻域，而且具有避免陷入局部最优解的能力。

2 初始持有资金有限条件下基于两阶段决策的基金价格控制模型及其求解

2.1 基本假设

为了研究方便，给出以下假设：

A1 :在某一交易时间段内，某一基金的交易者只有一个“庄家”型基金投资者和无穷多单个散户基金投资者；

A2 :基金的买卖均在离散的时刻进行，在每一时刻，“庄家”型基金投资者和个体投资者只能进行一次买或卖；

A3 :所有个体投资者在基金交易过程中的整体行为服从正态分布；

A4 :资本市场是完全的，不考虑基金交易中的交易费用和税收，投资者都是理性的；

A5:个体投资者卖出仅根据持有基金的收益率的大小，买入仅根据基金价格上涨速率的大小；

A6:在交易时间段的初始时刻“庄家”型基金投资者持有该基金的金额为零；

2.2 基于两阶段决策的基金价格控制模型

前已述及，我们可将“庄家”型基金投资者的基金价格控制决策分为两个阶段: 第一阶段为在给定各时刻基金期望收益率及收益离差的条件下, 确定“庄家”型基金投资者在某一交易时段内各个时刻的最优投资值；第二阶段则以第一阶段得到的各时刻的最优投资值为约束, 以现金收益的最大化来确定最优基金价格控制序列。

2.2.1 “庄家”型基金投资者第i时刻的最优投资值

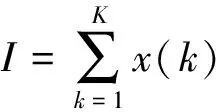
(1)

在该交易时间段的收益函数为：

(2)

假设投资者期望最小化风险的同时使得自己的收益最大，因此建立如下使“庄家”型基金投资者期望收益最大、收益平均绝对离差最小的双目标模型[9-11]：

(3)

取0<λ<1，它表示投资者的风险偏好系数，λ越大表示投资者越厌恶风险，式(3)可变换为如下的单目标模型Γ1:

(4)

对此有如下的定理

定理1：对于任意的λ∈(0,1)，模型Γ1的最优解为：

(5)

(6)

其中Θ(λ)满足如下条件：

(a)如果存在一个整数η∈[0,K-2]，

当k=1,2,…,η，有：

(7)

当k=η+1，有：

(8)

那么Θ(λ)={K,K-1,…,K-η}；

(b)如果任意一个整数η∈[0,K-2]不能满足条件(7)、(8)，那么Θ(λ)={K,K-1,…,2,1}。

证明：对模型Γ1应用库恩-塔克条件。首先引入拉格郎日函数

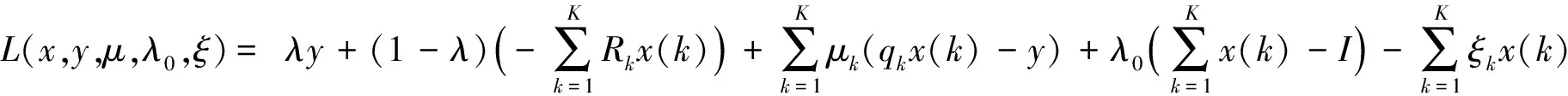
(9)

进一步由库恩-塔克条件可得以下各式：

(10)

(11)

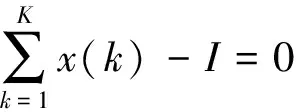
(12)

μk(qkx(k)-y)=0

(13)

ξkx(k)=0

(14)

μk≥0

(15)

ξk≥0

(16)

k=1,2,…,K

(17)

定义Θ(λ)={k|μk>0}，对任意的k∉Θ(λ)，令x(k)=0。由式(13)知，如果k∈Θ(λ)，那么有x(k)=y/qk。因此，结合式(12)得到：

(18)

(19)

由式(14)知，当x(k)>0时，那么ξk=0。对于k∈Θ(λ)，由式(11)可以得到：

(20)

结合式(10)得到

λ=∑l∈Θ(λ)(1/ql)[(1-λ)Rk-λ0)]，因此

(21)

对于k∈Θ(λ)，由式(20)得到:

(22)

对于任意的k∉Θ(λ):

ξk=-(1-λ)Rk+μkqk+λ0=-(1-λ)Rk+λ0

(23)

如果集合Θ(λ)中元素能使得式(22)和式(23)表示的μk、ξk非负，那么由式(18)、(19)得到的解将满足库恩-塔克条件(10)～(16)。

首先证明定理1中的(a), 由式(22)变形得到：

(24)

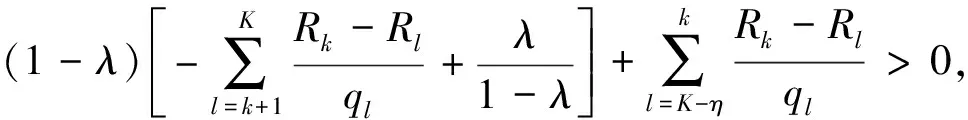
另一方面，对于k=1,2,…,K-η-1，类似于由式(24)得到μk≥0的证明方法，进一步由式(21)和式(23)得：

(25)

根据式(24)、(25)可以得到μk≥0，ξk≥0，这表明模型Γ1中的库恩-塔克条件(15)、(16)可以满足，同时结合式(18)、(19)可知Γ1的库恩-塔克(10)～(14)也可满足，因此(a)得证。

运用同样的方法，可以证明定理1中的(b)。如果任意一个整数η∈[0,K-2]不能满足式(7)、(8)，那么可证明由式(18)、(19)及集合Θ(λ)={K,K-1,…,2,1}得到的解将满足模型Γ1的库恩-塔克条件，限于篇幅，从略。

2.2.2 基金价格控制模型

在第k时刻“庄家”型基金投资者的净交易量ћ(k)为散户基金投资者的卖出量s(k)与买入量b(k)之差，即：

ћ(k)=s(k)-b(k)

(26)

其中：

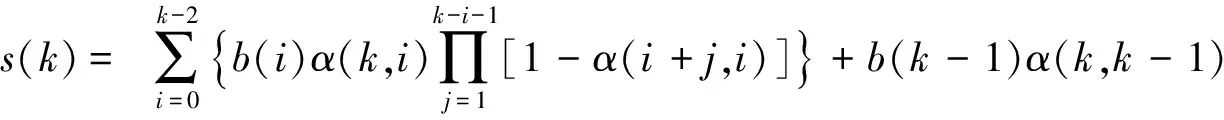
(27)

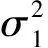
(28)

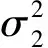
(29)

为散户基金投资者在第k时刻买入的百分比。

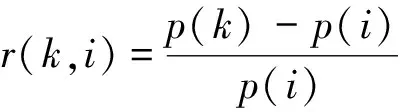
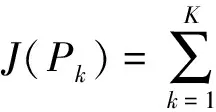
(30)

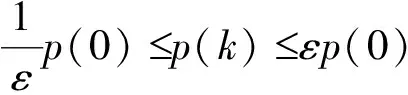
(31)

(32)

初始条件：p(0)=ζ

(33)

2.3 模型Γ3的求解

依据式(26)、(27)、(28)、(29)可知，ћ(k)为p(k)的非线性函数，因此模型Γ3为一个带约束条件的非线性规划问题，由于所建方程的复杂性，很难得到解析解。一般状况下对于此类问题可采用惩罚函数法进行求解，从而将带约束的非线性规划问题的求解，转化为求解一系列无约束极值问题，进而得到原问题的最优解或近优解。但是随着惩罚因子趋于无穷大或零，目标函数值随着迭代点向最优点靠近而逐渐变坏[13-15]，使一般无约束优化方法失效。文献[16]提出了一种改进的遗传算法来求解带约束的非线性规划问题，利用该方法不但能够收敛到最优解的邻域，而且具有避免陷入局部最优解的能力，而且该方法采取全方位搜索方式，避免陷入局部最优；步长的选取具有随机性，且均值衰减。由于唐加福等[16]已验证了该改进遗传算法的优点，对此不再赘述，下面说明该算法的具体求解过程。

记Γ3中的元素Pk∈Q={Pk∈EK|gk(Pk)0,k=1,2,…,K}，其中gk(Pk)0为约束函数。而基于惩罚函数提出的改进遗传算法的基本思想是：首先随机产生种群(假设种群大小为NP)，对于每个个体Pk，如果Pk∉Q，置一个很小的适应性值与之对应(相当于惩罚)；每个个体在迭代中按滚动轮策略被选取,且沿权重梯度方向经变异产生子个体。随着迭代步数的增加，具有较小适应性值的子个体逐渐被淘汰,而留下来的则是适应性值较大的子个体。对于个体Pk,如果Pk∈Q,则沿目标函数的梯度方向J(Pk)搜索,可使目标函数得到改进。如果Pk∉Q,说明Pk不在可行域内,令:

Λ={k|gk(Pk)0,Pk∈EK}

(34)

对于k∈Λ，如果Pk沿负梯度方向-gk(Pk)移动,可使子个体Pk满足gk(Pk)0。构造权重梯度方向[11]，用D(Pk)表示:

(35)

其中ωk是梯度方向权重，定义为：

(36)

(37)

gmax(Pk)=max{gk(Pk),k=1,2,…,K}

(38)

其中，δ是一个很小的整数。

p(k,s)沿权重梯度方向D(Pk)变异产生子个体p(k,s+1)可以描述为

p(k,s+1)=p(k,s)+β(s)D(p(k,s))

(39)

其中,β(s)是均匀分布随机数步长，由随机数发生器产生。

从gmax(Pk)=max{gk(Pk),k=1,2,…,K}可以看出，gmax(Pk)反映了点Pk与可行域Q的关系信息。如果gmax(Pk)0，表明Pk∈Q;否则,gmax(Pk)>0，且gmax(Pk)越大，表明Pk∈Q的性能越差，即Pk越远离可行域。目标函数按如下计算：

(40)

其中，L是预先给定的很大的正数。

从上式还可以看出,如果gmax(Pk)>0，则重新赋给一个很小的目标函数值，但非零，以便在以后的迭代中有很小的概率被选取作为母体产生子个体。此外，可以发现，如果Pk∈Q，则D(Pk)=J(Pk)，沿D(Pk)方向搜索,目标函数不断得到改进,进而达到最优解的附近；如果Pk∉Q,gk(Pk)越大，偏离可行域越远，得到的权重越大，使得子个体向可行域方向搜索，从而达到可行域的边界。

基于以上的分析，该算法的计算复杂性为O(NP*NG*K3)，基本步骤为：

(1)确定基因表达式。用决策变量Pk的k维实向量表示子个体,即Pk=(p(1),p(2),…,p(k))。

(2)确定适应性函数与选择策略。选取适应性函数ψ(Pk)=J(Pk)+θ，其中,θ是一个小的正数，用滚动轮策略选择个体。

(4)停止规则。根据计算精度的要求，确定最大的迭代步骤NG。

3 算法释例

在此给出模型的基本求解过程。首先确定初始持有资金限制条件下“庄家”型基金投资者第i时刻的最优投资值。取K=10，令A=1，“庄家”型基金投资者在该交易时段前持有的基金额为零，期初持有的投入资金I=0.25，λ=0.8，为节省篇幅(第一阶段具体求取从略)，依据定理1求得

(x(0)*,x(1)*,x(2)*,x(3)*,x(4)*,x(5)*,x(6)*,x(7)*,x(8)*,x(9)*)=

(0.0893,0.0357,0.0298,0.0198,0.0179,0.0149,

0.0128,0.0112,0.0099,0.0089)

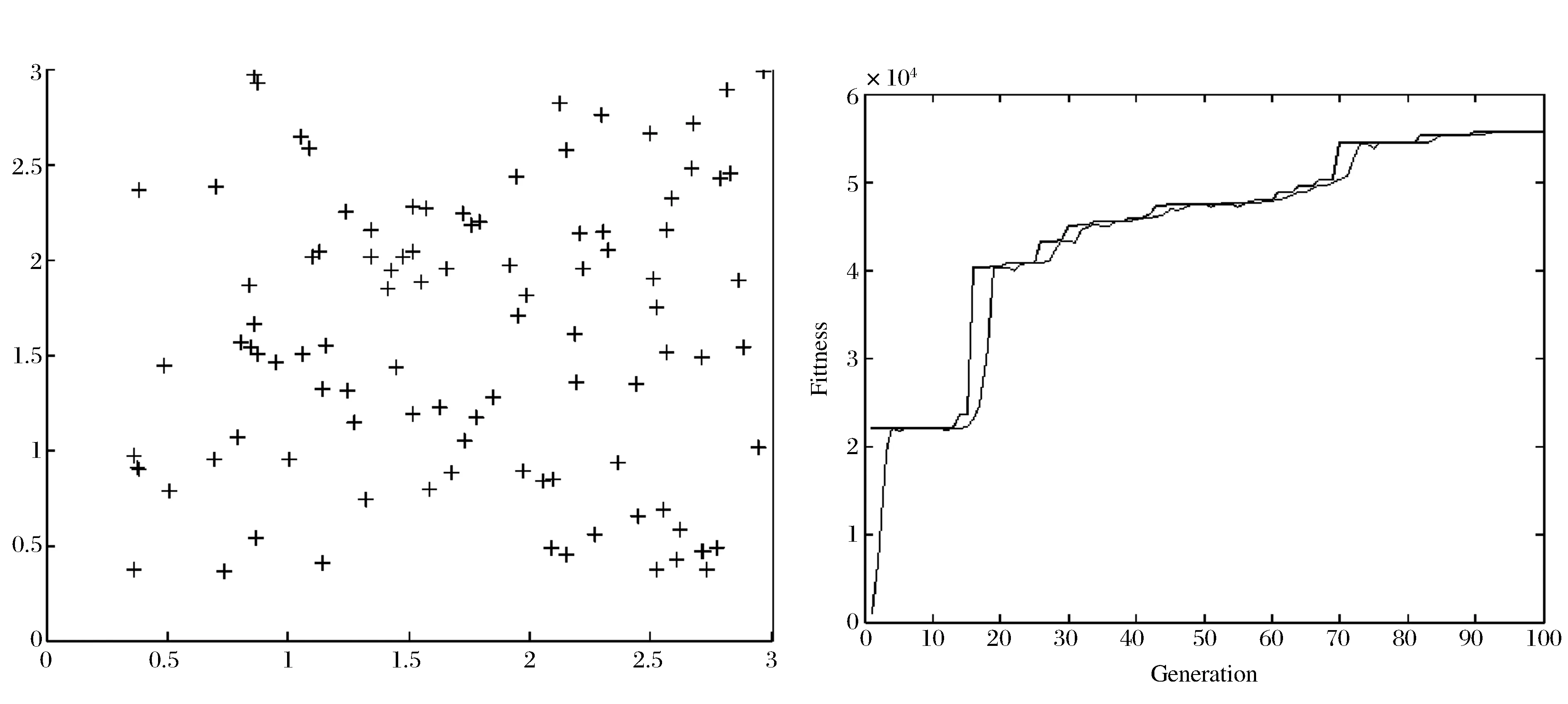
图1 遗传算法迭代次数及进化图

对于第二阶段所建立的模型则采取MATLAB7.0软件进行遗传算法编程来求解。不失一般性，首先给定参数r*=0.32，σ1=0.21，υ*=0.45，σ2=0.35，ε=3，ζ=1，M=0。进一步使用文中所给的遗传算法，取L=106,δ=θ=10-6，最大迭代次数为200次，种群为100个，将第一阶段求得的(x(0)*,x(1)*,x(2)*,x(3)*,x(4)*,x(5)*,x(6)*,x(7)*,x(8)*,x(9)*)作为相应的约束，解得价格序列为

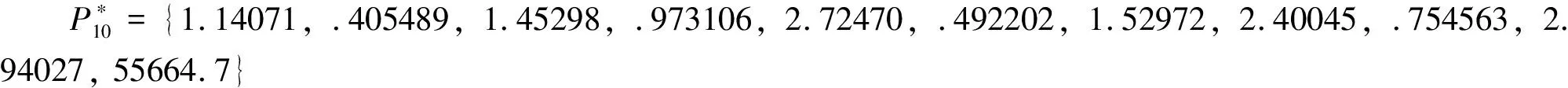
4 研究结果分析

已有的文献对于封闭式基金价格的研究多是从基金价格的形成过程如何受市场因素的影响来探讨[2-8]，例如Flynn[2]讨论了噪声交易、套利与资产价格对于美国封闭式基金折价的影响，Shane[3]讨论了信号传递、差异化策略与基金折价的关系，张世英、王东[4]研究了投资基金的价格监管和风险控制问题，赵秀娟等[7]分析了深市基金指数(封闭式基金价格指数)与其它证券市场产品开在波动上的关联性问题。中国基金市场透明度不高、疏于监管、相关法律法规欠缺使得封闭式基金的价格也必然存在如同股票市场一样的价格操纵现象，即大资金投资者控制基金价格的“庄家”现象，那么在此种情况下“庄家”型基金投资者采取何种策略控制封闭式基金的价格，从而达到盈利目的是一个值得研究的课题，而国内外文献对于此方面几乎没有涉及，所以这正是本文选题的独特之处。

俞雪飞等[12]提出了一种单一证券的庄家控制模型，区别于前者，在本研究中我们考虑了“庄家”型基金投资者初始资金有限的状况，另外我们将庄家控制基金价格的决策过程分为两个阶段：第一阶段为在给定各时刻基金期望收益率及收益离差的条件下, 确定“庄家”型基金投资者在某一交易时段内各个时刻的最优投资值；第二阶段则以第一阶段得到的各时刻的最优投资值为约束，以现金收益的最大化来确定最优基金价格控制序列。这样的阶段划分使得价格控制更符合实际的决策过程，因为无论是散户还是机构投资者，各阶段的持有资金额度及投资收益期望值是不同的，那么这也成为实际投资决策中的约束条件。另外，俞雪飞等[12]没有给出所建模型的具体求解方法，由于本文所建的模型是带约束条件的非线性规划问题，很难得到解析解。一般状况下对于此类问题采用惩罚函数法进行求解，但随着惩罚因子趋于无穷大或零，目标函数值随着迭代点向最优点靠近而失效。有鉴于此，本文引进了遗传算法进行求解，有效的避免陷入局部最优。另外，从具体计算结果的仿真图形来看，较符合“庄家”投资者“高抛低吸”的实际投资过程。

5 结语

在中国目前这种基金交易市场条件下，尤其在国家“封转开”政策的逐渐推行下，如何监管并有效抑制封闭式基金交易过程中的投机行为是一个非常值得研究的课题。在初始持有资金有限的状况下，文中所给的两阶段模型基本上与基金交易过程中“庄家”型基金投资者控制基金价格行为非常吻合，该类型的基金交易者可能在确定某一交易时间段内各时刻基金期望收益率及收益离差的前提下，合理地分配各时刻的资金投入值；然后再以各时刻最优投资值为约束，以“庄家”型基金投资者在该交易时间段内的现金支付为极小值建立目标函数，最后获得价格控制最优策略。此外，如果进行历史数据模拟可掌握参数r*，σ1，υ*，σ2，结合基金交易中的实际市场规律，就可以发现实际交易中的基金买卖是否存在“庄家”型基金投资者操纵基金价格的行为，预计“庄家”型基金投资者控制基金价格将采取的未来价格走势等。这对于金融部门加强封闭式基金的市场监管，防止封闭式基金交易中的过分操纵基金价格走势行为的发生是极其具有实用价值的。

参考文献：

[1] 陈绍胜.中国基金“封转开”的路径选择与模式探讨[J].南方金融,2006,2:59-61.

[2] Flynn S M.Noise-trading, costly arbitrage, and asset prices: Evidence from US closed- end funds [J].Journal of Financial Markets,2012, 15(1): 108-125.

[3] Shane A J, Ji-Chai L, Kyojik R S.Dividend policy, signaling, and discounts on closed-end funds [J].Journal of Financial Economics, 2006, 81(3): 539-562.

[4] 张世英,王 东.基金投资行为及其监管的模糊随机理论研究[J] .管理科学学报,2000,3(1):58-60.

[5] 宋颂兴.封闭型证券投资基金定价研究[J] .数量经济技术经济研究,1999,(9):26-28.

[6] 肖国荣.BP神经网络在基金价格预测中的应用研究[J].计算机仿真,2011, 28(3):373-376.

[7] 赵秀娟,朱凯誉,汪寿阳.封闭式基金价格指数波动溢出效应研究——以深市基金指数为例[J].中国管理科学,2011,19(6):1-9.

[8] 王良,冯涛.中国ETF基金价格“已实现”波动率、跟踪误差之间的Granger关系研究[J].中国管理科学,2012, 20(1):59-70.

[9] Tsukuma H.Shrinkage minimax estimation and positive-part rule for a mean matrix in an elliptically contoured distribution [J].Statistics & Probability Letters, 2010, 80(3):215-220.

[10]Cai Xiaoqiang, Tao K L,Yang Xiaoqi, et al.Portfolio optimization under a minimaxrule[J].Management Science,2000,46(7): 957-972.

[11]Ko C H, Wang Shufan.Precast production scheduling using multi-objective genetic algorithms[J].Expert Systems with Applications, 2011, 38 (7): 8293-8302.

[12]俞雪飞,汪温泉,潘德惠.非有效证券市场庄家控股模型[J].系统工程学报,2003,18(4):343-347.

[13]燕乐纬,陈树辉.基于改进遗传算法的非线性方程组求解[J].中山大学学报(自然科学版),2011,1:9-13.

[14]李宏,王宇平,焦永昌.解非线性两层规划问题的新的遗传算法及全局收敛性[J].系统工程理论与实践,2005,3:62-71.

[15]田新时,刘磊.基于改进遗传算法的开放式基金市场价值溢价研究[J].管理工程学报,2008, 8(2):160-163.

[16]唐加福,汪定伟.一种求解非线性规划问题的改进遗传算法[J].东北大学学报,1997,18(3):390-392.